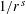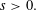Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Farkas, Bálint
Nagy, Béla
and
Révész, Szilárd Gy.
2018.
A minimax problem for sums of translates on the torus.
Transactions of the London Mathematical Society,
Vol. 5,
Issue. 1,
p.
1.
Erdélyi, Tamás
2020.
Reverse Markov- and Bernstein-type inequalities for incomplete polynomials.
Journal of Approximation Theory,
Vol. 251,
Issue. ,
p.
105341.
Dubinin, V. N.
2020.
Pólya–Schur Inequality and the Green Energy of a Discrete Charge.
Doklady Mathematics,
Vol. 101,
Issue. 3,
p.
192.
Erdélyi, Tamás
2021.
Turán-Type Reverse Markov Inequalities for Polynomials with Restricted Zeros.
Constructive Approximation,
Vol. 54,
Issue. 1,
p.
35.
Farkas, Bálint
Nagy, Béla
and
Révész, Szilárd Gy.
2025.
Fenton type minimax problems for sum of translates functions.
Journal of Mathematical Analysis and Applications,
Vol. 543,
Issue. 2,
p.
128931.