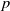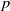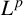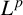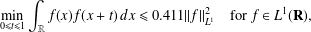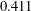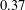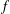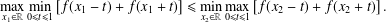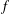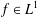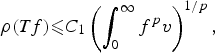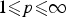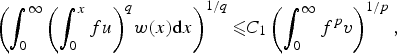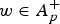Refine search
Actions for selected content:
37 results
Sharp Hardy and spectral gap inequalities on special irreversible Finsler manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-36
-
- Article
- Export citation
Existence of minimizers of the stability constant of Caffarelli–Kohn–Nirenberg inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-23
-
- Article
- Export citation
Improvement of some discrete Hardy inequalities with variants
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 114-130
- Print publication:
- January 2025
-
- Article
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1093-1134
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multidimensional Frank–Laptev–Weidl improvement of the hardy inequality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 151-167
-
- Article
- Export citation
On a class of Hilbert-type inequalities in the whole plane involving some classical kernel functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 833-846
-
- Article
- Export citation
SOME
 $\boldsymbol {L^p}$-HARDY AND
$\boldsymbol {L^p}$-HARDY AND  $\boldsymbol {L^p}$-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
$\boldsymbol {L^p}$-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 79-98
- Print publication:
- August 2022
-
- Article
- Export citation
EMBEDDING THEOREM OF THE WEIGHTED SOBOLEV–LORENTZ SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 358-375
- Print publication:
- May 2022
-
- Article
- Export citation
Counting matchings via capacity-preserving operators
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation
Sharp Caffarelli–Kohn–Nirenberg inequalities on Riemannian manifolds: the influence of curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 102-127
- Print publication:
- February 2022
-
- Article
- Export citation
Hardy type inequalities on closed manifolds via Ricci curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 993-1020
- Print publication:
- June 2021
-
- Article
- Export citation
EXTENSIONS OF AUTOCORRELATION INEQUALITIES WITH APPLICATIONS TO ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2020, pp. 451-461
- Print publication:
- December 2020
-
- Article
- Export citation
Embeddings of homogeneous Sobolev spaces on the entire space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 296-328
- Print publication:
- February 2021
-
- Article
- Export citation
INEQUALITIES FOR DRAGOMIR’S MAPPINGS VIA STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 240-250
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
A new proof of the Hardy–Rellich inequality in any dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 2894-2904
- Print publication:
- December 2020
-
- Article
- Export citation
An optimal improvement for the Hardy inequality on the hyperbolic space and related manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1699-1736
- Print publication:
- August 2020
-
- Article
- Export citation
Weighted norm inequalities for positive operators restricted on the cone of λ-quasiconcave functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 17-39
- Print publication:
- February 2020
-
- Article
- Export citation
Compactness of Commutators of One-Sided Singular Integrals in Weighted Lebesgue Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 655-665
-
- Article
- Export citation