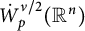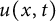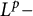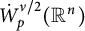1 Introduction
Analytic inequalities, including Sobolev inequalities, logarithmic Sobolev inequalities, Hardy inequalities, and their fractional counterparts, play crucial roles in harmonic analysis, mathematical physics, and partial differential equations (PDEs). Interested readers can explore the works of Beckner and Pearson [Reference Beckner and Pearson4], Cotsiolis and Tavoularis [Reference Cotsiolis and Tavoularis9], Talenti [Reference Talenti36], Xiao and Zhai [Reference Xiao and Zhai42], and the references therein for further insights into Sobolev-type inequalities.
Trace inequalities of Sobolev type, logarithmic Sobolev type, and Hardy type, particularly in the context of operators and equations, have also been extensively studied. Xiao established sharp fractional Sobolev trace inequalities linked to the Poisson equation in [Reference Xiao39]. Einav and Loss [Reference Einav and Loss15] proved Sobolev trace inequalities involving the projector
![]() $\tau _k$
. More recently, Li, Hu, and Zhai [Reference Li, Hu and Zhai27] contributed to the field by establishing fractional Sobolev, logarithmic Sobolev, and Hardy trace inequalities associated with fractional harmonic extensions.
$\tau _k$
. More recently, Li, Hu, and Zhai [Reference Li, Hu and Zhai27] contributed to the field by establishing fractional Sobolev, logarithmic Sobolev, and Hardy trace inequalities associated with fractional harmonic extensions.
In this article, our objective is to establish Sobolev, logarithmic Sobolev, and Hardy trace-type inequalities associated with the solution of the following time-space fractional equations:
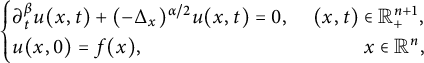 $$ \begin{align} \begin{cases} \partial^{\beta}_t u(x,t)+(-\Delta_x)^{\alpha/2}u(x,t)=0,&\ (x,t)\in \mathbb{R}^{n+1}_+,\\ u(x,0)=f(x),&\qquad\ \ \ x\in\mathbb R^{n},\\ \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \partial^{\beta}_t u(x,t)+(-\Delta_x)^{\alpha/2}u(x,t)=0,&\ (x,t)\in \mathbb{R}^{n+1}_+,\\ u(x,0)=f(x),&\qquad\ \ \ x\in\mathbb R^{n},\\ \end{cases} \end{align} $$
where
![]() $\alpha>n$
and
$\alpha>n$
and
![]() $\beta \in (0,1]$
. Here, the Caputo fractional derivative, denoted by
$\beta \in (0,1]$
. Here, the Caputo fractional derivative, denoted by
![]() $\partial ^{\beta }_{t}$
, is defined as
$\partial ^{\beta }_{t}$
, is defined as
Additionally, the fractional Laplace operator
![]() $(-\Delta _x)^{\alpha /2}$
in
$(-\Delta _x)^{\alpha /2}$
in
![]() $\mathbb {R}^n$
is defined on the Schwartz class through the Fourier transform:
$\mathbb {R}^n$
is defined on the Schwartz class through the Fourier transform:
When
![]() $\beta =1,$
the equations (1.1) become fractional diffusion equations:
$\beta =1,$
the equations (1.1) become fractional diffusion equations:
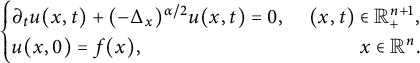 $$ \begin{align} \begin{cases} \partial_t u(x, t)+ (-\Delta_x)^{\alpha/2}u(x,t) = 0,&\ (x,t)\in \mathbb R^{n+1}_{+},\\ u(x, 0) = f(x),&\qquad\ \ \ x\in\mathbb R^{n}. \\ \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \partial_t u(x, t)+ (-\Delta_x)^{\alpha/2}u(x,t) = 0,&\ (x,t)\in \mathbb R^{n+1}_{+},\\ u(x, 0) = f(x),&\qquad\ \ \ x\in\mathbb R^{n}. \\ \end{cases} \end{align} $$
The Carleson embedding associated with (1.2) has been extensively studied in various works, including Adams and Hedberg [Reference Adams and Hedberg1], Chang and Xiao [Reference Chang and Xiao8], Liu, Wu, Xiao, and Yuan [Reference Liu, Wu, Xiao and Yuan29], Xiao [Reference Xiao38], Xiao and Zhai [Reference Xiao and Zhai42], and Zhai [Reference Zhai46]. These studies have contributed to the understanding of the Carleson embedding properties related to the fractional diffusion equations. When
![]() $\beta =1$
and
$\beta =1$
and
![]() $\alpha =2$
, the equation (1.1) corresponds to the classical heat equation, a fundamental equation with widespread applications in various fields, including mathematics, physics, fluid dynamics, and engineering.
$\alpha =2$
, the equation (1.1) corresponds to the classical heat equation, a fundamental equation with widespread applications in various fields, including mathematics, physics, fluid dynamics, and engineering.
If
![]() $\beta =1$
and
$\beta =1$
and
![]() $\alpha \in (0,2)$
, the equations (1.1) transform into the spatial fractional heat equation. This equation has found applications in the study of fluid dynamics, contributing to the understanding of heat transfer processes.
$\alpha \in (0,2)$
, the equations (1.1) transform into the spatial fractional heat equation. This equation has found applications in the study of fluid dynamics, contributing to the understanding of heat transfer processes.
When
![]() $\beta \in (0,1)$
and
$\beta \in (0,1)$
and
![]() $\alpha =2$
, the equations (1.1) become the so-called “time fractional” heat equations:
$\alpha =2$
, the equations (1.1) become the so-called “time fractional” heat equations:
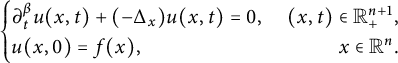 $$ \begin{align} \begin{cases} \partial^{\beta}_t u(x,t)+(-\Delta_x)u(x,t)=0,&\ (x,t)\in \mathbb{R}^{n+1}_+,\\ u(x,0)=f(x),&\qquad\ \ \ x\in\mathbb R^{n}. \\ \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \partial^{\beta}_t u(x,t)+(-\Delta_x)u(x,t)=0,&\ (x,t)\in \mathbb{R}^{n+1}_+,\\ u(x,0)=f(x),&\qquad\ \ \ x\in\mathbb R^{n}. \\ \end{cases} \end{align} $$
The equations (1.3) exhibit sub-diffusive behavior and are associated with anomalous diffusion or diffusion in non-homogeneous media with random fractal structures.
The introduction of the time-fractional derivative
![]() $\partial ^{\beta }_{t}$
by Caputo in [Reference Caputo7] marked a significant development for investigating the analytic expression of a linear dissipative mechanism. In mathematical physics and engineering, Caputo fractional derivatives and their generalizations have become instrumental in addressing unconventional physical phenomena, capturing the attention of numerous researchers. For further exploration of generalizations of Caputo derivatives, readers can refer to works by Bernardis, Martín-Reyes, Stinga, and Torrea [Reference Bernardis, Martín-Reyes, Stinga and Torrea5], Gorenflo, Luchko, and Yamamoto [Reference Gorenflo, Luchko and Yamamoto18], Kilbas, Srivastava, and Trujillo [Reference Kilbas, Srivastava and Trujillo25], and Li and Liu [Reference Li and Liu26].
$\partial ^{\beta }_{t}$
by Caputo in [Reference Caputo7] marked a significant development for investigating the analytic expression of a linear dissipative mechanism. In mathematical physics and engineering, Caputo fractional derivatives and their generalizations have become instrumental in addressing unconventional physical phenomena, capturing the attention of numerous researchers. For further exploration of generalizations of Caputo derivatives, readers can refer to works by Bernardis, Martín-Reyes, Stinga, and Torrea [Reference Bernardis, Martín-Reyes, Stinga and Torrea5], Gorenflo, Luchko, and Yamamoto [Reference Gorenflo, Luchko and Yamamoto18], Kilbas, Srivastava, and Trujillo [Reference Kilbas, Srivastava and Trujillo25], and Li and Liu [Reference Li and Liu26].
Fractional derivatives offer distinct advantages compared to integer-order derivatives. They capture the history-dependent development of a system function more accurately due to global correlation. The fractional derivative model also addresses the limitations of classical differential model theory, providing better agreement with experimental results. Additionally, in describing complex physical and mechanical problems, fractional-order models often offer clarity and conciseness compared to nonlinear models. Leveraging these advantages, time-fractional calculus finds widespread application in various scientific branches, including statistical mechanics, theoretical physics, theoretical neuroscience, the theory of complex chemical reactions, fluid dynamics, hydrology, and mathematical finance. For an extensive list of references, readers can consult Khoshnevisan [Reference Khoshnevisan24].
In Section 2.2, we utilize the subordinative formula to estimate the higher-order derivatives of the integral kernels associated with the fractional heat semigroups
![]() ${e^{-t(-\Delta _x)^{\alpha /2}}}$
for
${e^{-t(-\Delta _x)^{\alpha /2}}}$
for
![]() $t>0$
, denoted by
$t>0$
, denoted by
![]() $K_{\alpha ,t}(\cdot )$
(refer to Lemmas 2.2 and 2.8). The time-space fractional heat kernel, denoted by
$K_{\alpha ,t}(\cdot )$
(refer to Lemmas 2.2 and 2.8). The time-space fractional heat kernel, denoted by
![]() $G_{t}^{\alpha ,\beta }(\cdot )$
, is introduced as the fundamental solution to equations (1.1). Through the representation (2.1), we establish that for
$G_{t}^{\alpha ,\beta }(\cdot )$
, is introduced as the fundamental solution to equations (1.1). Through the representation (2.1), we establish that for
![]() $m\in \mathbb {Z}_{+}$
, the following estimates hold:
$m\in \mathbb {Z}_{+}$
, the following estimates hold:
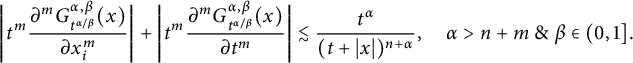 $$ \begin{align*} \Bigg|t^m\frac{\partial^mG^{\alpha,\beta}_{t^{\alpha/\beta}}(x)}{\partial x_i^m}\Bigg|+\Bigg| t^m\frac{\partial^mG^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)}{\partial t^m}\Bigg| \lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}},\quad \alpha>n+m\ \&\ \beta\in (0,1]. \end{align*} $$
$$ \begin{align*} \Bigg|t^m\frac{\partial^mG^{\alpha,\beta}_{t^{\alpha/\beta}}(x)}{\partial x_i^m}\Bigg|+\Bigg| t^m\frac{\partial^mG^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)}{\partial t^m}\Bigg| \lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}},\quad \alpha>n+m\ \&\ \beta\in (0,1]. \end{align*} $$
These estimates are detailed in Propositions 2.10 and 2.11.
Let
![]() $C_0^{\infty }(\mathbb {R}^n)$
represents the space of infinitely differentiable functions on
$C_0^{\infty }(\mathbb {R}^n)$
represents the space of infinitely differentiable functions on
![]() $\mathbb R^{n}$
with compact support. For
$\mathbb R^{n}$
with compact support. For
![]() $\nu \in (0,1)$
and
$\nu \in (0,1)$
and
![]() $p\in (1,n/\nu )$
, the homogeneous Sobolev space
$p\in (1,n/\nu )$
, the homogeneous Sobolev space
![]() $\dot {W}^{\nu }_p(\mathbb {R}^n)$
is defined as the completion of
$\dot {W}^{\nu }_p(\mathbb {R}^n)$
is defined as the completion of
![]() $C_0^{\infty }(\mathbb R^{n})$
with respect to the norm
$C_0^{\infty }(\mathbb R^{n})$
with respect to the norm
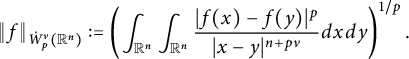 $$ \begin{align*}\|f\|_{\dot{W}^{\nu}_p(\mathbb{R}^n)}:= \left(\int_{\mathbb{R}^n}\int_{\mathbb{R}^n}\frac{|f(x)-f(y)|^p}{|x-y|^{n+p\nu}}dxdy\right)^{1/p}.\end{align*} $$
$$ \begin{align*}\|f\|_{\dot{W}^{\nu}_p(\mathbb{R}^n)}:= \left(\int_{\mathbb{R}^n}\int_{\mathbb{R}^n}\frac{|f(x)-f(y)|^p}{|x-y|^{n+p\nu}}dxdy\right)^{1/p}.\end{align*} $$
Specially, when
![]() $p=2$
,
$p=2$
,
![]() $\dot {W}_{2}^{\nu }(\mathbb {R}^n)$
is also denoted by
$\dot {W}_{2}^{\nu }(\mathbb {R}^n)$
is also denoted by
![]() $\dot {H}^{\nu }(\mathbb {R}^n).$
Moreover,
$\dot {H}^{\nu }(\mathbb {R}^n).$
Moreover,
![]() $\dot {W}^{-\nu }_{p'}(\mathbb {R}^n)$
is the dual of
$\dot {W}^{-\nu }_{p'}(\mathbb {R}^n)$
is the dual of
![]() $\dot {W}^{\nu }_{p}(\mathbb {R}^n).$
In Section 3, considering f in the homogeneous Sobolev space
$\dot {W}^{\nu }_{p}(\mathbb {R}^n).$
In Section 3, considering f in the homogeneous Sobolev space
![]() $\dot {H}^{\nu /2}(\mathbb R^{n})$
, and utilizing the Fourier transform of
$\dot {H}^{\nu /2}(\mathbb R^{n})$
, and utilizing the Fourier transform of
![]() $G^{\alpha ,\beta }_t(\cdot )$
, we establish equivalent characterizations of the norm of
$G^{\alpha ,\beta }_t(\cdot )$
, we establish equivalent characterizations of the norm of
![]() $\dot {H}^{\nu /2}(\mathbb R^{n})$
as follows:
$\dot {H}^{\nu /2}(\mathbb R^{n})$
as follows:
Here,
![]() $\widetilde {\nabla }_{x}^{m}:=(\partial ^m_{x_1},\partial ^m_{x_2},\ldots ,\partial ^m_{x_n})$
(refer to (3.4)). Building upon this result, we establish fractional Sobolev, logarithmic Sobolev, and Hardy trace-type inequalities. For any
$\widetilde {\nabla }_{x}^{m}:=(\partial ^m_{x_1},\partial ^m_{x_2},\ldots ,\partial ^m_{x_n})$
(refer to (3.4)). Building upon this result, we establish fractional Sobolev, logarithmic Sobolev, and Hardy trace-type inequalities. For any
![]() ${f\in \dot {H}^{\nu /2}(\mathbb {R}^n)}$
and
${f\in \dot {H}^{\nu /2}(\mathbb {R}^n)}$
and
![]() $u(x,t)=G^{\alpha ,\beta }_{t}\ast f(x)$
, the fractional Sobolev trace inequality is given by
$u(x,t)=G^{\alpha ,\beta }_{t}\ast f(x)$
, the fractional Sobolev trace inequality is given by
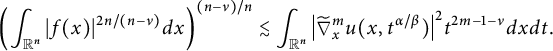 $$ \begin{align} \left( \int_{\mathbb{R}^n} |f(x)|^{2n/(n-\nu)} dx\right)^{(n-\nu)/n}\lesssim \int_{\mathbb{R}^n}\big| \widetilde{\nabla}^{m}_{x}u(x,t^{\alpha/\beta})\big|^2 t^{2m-1-\nu}dxdt. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n} |f(x)|^{2n/(n-\nu)} dx\right)^{(n-\nu)/n}\lesssim \int_{\mathbb{R}^n}\big| \widetilde{\nabla}^{m}_{x}u(x,t^{\alpha/\beta})\big|^2 t^{2m-1-\nu}dxdt. \end{align} $$
This result is detailed in Theorem 3.1. Furthermore, when
![]() $\|f\|_{L^2(\mathbb {R}^n)}=1$
, the following fractional logarithmic Sobolev inequality and the fractional Hardy inequality (or the Kato inequality) are established:
$\|f\|_{L^2(\mathbb {R}^n)}=1$
, the following fractional logarithmic Sobolev inequality and the fractional Hardy inequality (or the Kato inequality) are established:
 $$ \begin{align} \begin{cases}\displaystyle \exp\left( \frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)dx\right)\lesssim \int_{\mathbb{R}^n}\big| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\big|^2 t^{2m-1-\nu}dxdt; \\ \qquad\qquad\quad\quad\quad\displaystyle\int_{\mathbb{R}^n} |f(x)|^2\frac{dx}{|x|^\nu}\lesssim \int_{\mathbb{R}^n}\big| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\big|^2 t^{2m-1-\nu}dxdt. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases}\displaystyle \exp\left( \frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)dx\right)\lesssim \int_{\mathbb{R}^n}\big| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\big|^2 t^{2m-1-\nu}dxdt; \\ \qquad\qquad\quad\quad\quad\displaystyle\int_{\mathbb{R}^n} |f(x)|^2\frac{dx}{|x|^\nu}\lesssim \int_{\mathbb{R}^n}\big| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\big|^2 t^{2m-1-\nu}dxdt. \end{cases} \end{align} $$
These results are detailed in Theorem 3.1. Xiao [Reference Xiao39] established inequalities akin to (1.4) and the first inequality of (1.5) for the Poisson extension. Li, Hu, and Zhai in [Reference Li, Hu and Zhai27] investigated corresponding inequalities related to the Caffarelli–Silvestre extensions. Inequalities similar to the second inequality of (1.5) have been examined in [Reference Beckner and Pearson4, Reference Eilertsen14, Reference Hajaiej, Yu and Zhai21, Reference Herbst23, Reference Nguyen34, Reference Xiao and Zhai42, Reference Yafaev43]. We will demonstrate that the right-hand side of (1.4) and (1.5) can be replaced by
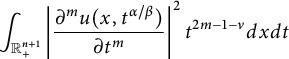 $$ \begin{align*}\int_{\mathbb R^{n+1}_{+}} \left|\frac{\partial^{m}u(x,t^{\alpha/\beta})}{\partial t^m}\right|^{2}t^{2m-1-\nu}dxdt\end{align*} $$
$$ \begin{align*}\int_{\mathbb R^{n+1}_{+}} \left|\frac{\partial^{m}u(x,t^{\alpha/\beta})}{\partial t^m}\right|^{2}t^{2m-1-\nu}dxdt\end{align*} $$
(see Theorem 3.3). Via a change of variable, inequalities similar to (1.4) and (1.5) in Theorems 3.1 and 3.3 can be proven for
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
and
$\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
and
![]() $u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x)$
(see Theorems 3.2 and 3.4).
$u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x)$
(see Theorems 3.2 and 3.4).
Moreover, Theorems 3.1 and 3.3 imply the following Sobolev-type trace inequalities:
 $$ \begin{align*}\left(\int_{\mathbb R^{n}}|f(x)|^{2n/(n-\nu)}dx\right)^{1-\nu/n}\lesssim \int_{\mathbb R^{n+1}_{+}}\left\{\left|t^{m}\widetilde{\nabla}_{x}^{m}u(x,t^{\alpha/\beta})\right|^{2}+ \left|t^{m}\frac{\partial^{m}u(x,t^{\alpha/\beta})}{\partial t^m}\right|^{2}\right\}\frac{dxdt}{t^{1+\nu}}\end{align*} $$
$$ \begin{align*}\left(\int_{\mathbb R^{n}}|f(x)|^{2n/(n-\nu)}dx\right)^{1-\nu/n}\lesssim \int_{\mathbb R^{n+1}_{+}}\left\{\left|t^{m}\widetilde{\nabla}_{x}^{m}u(x,t^{\alpha/\beta})\right|^{2}+ \left|t^{m}\frac{\partial^{m}u(x,t^{\alpha/\beta})}{\partial t^m}\right|^{2}\right\}\frac{dxdt}{t^{1+\nu}}\end{align*} $$
for
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
and
$\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
and
![]() $u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x).$
Via a change of variable, for
$u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x).$
Via a change of variable, for
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
and
$\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
and
![]() $u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x),$
the following equivalent version:
$u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x),$
the following equivalent version:
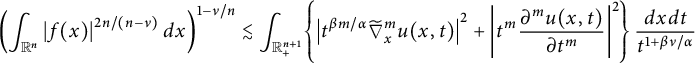 $$ \begin{align} \left(\kern-0.8pt \int_{\mathbb{R}^n}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim \int_{\mathbb{R}_{+}^{n+1}}\!\left\{\left|t^{\beta m/\alpha}\widetilde{\nabla}^{m}_{x}u(x,t)\right|^{2}+\left|t^{m}\frac{\partial^m u(x,t)}{\partial t^m}\right|^{2}\kern-1pt\right\}\frac{dxdt}{t^{1+\beta\nu/\alpha}} \end{align} $$
$$ \begin{align} \left(\kern-0.8pt \int_{\mathbb{R}^n}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim \int_{\mathbb{R}_{+}^{n+1}}\!\left\{\left|t^{\beta m/\alpha}\widetilde{\nabla}^{m}_{x}u(x,t)\right|^{2}+\left|t^{m}\frac{\partial^m u(x,t)}{\partial t^m}\right|^{2}\kern-1pt\right\}\frac{dxdt}{t^{1+\beta\nu/\alpha}} \end{align} $$
can be deduced from Theorems 3.2 and 3.4 immediately.
To generalize the Sobolev-type trace inequalities in Theorem 3.1 to
![]() $\dot {W}_p^{\nu /2}(\mathbb {R}^n),$
in Theorem 3.10, we characterize
$\dot {W}_p^{\nu /2}(\mathbb {R}^n),$
in Theorem 3.10, we characterize
![]() $\dot {W}_p^{\nu /2}(\mathbb {R}^n)$
as follows:
$\dot {W}_p^{\nu /2}(\mathbb {R}^n)$
as follows:
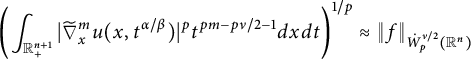 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)} \end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)} \end{align*} $$
and
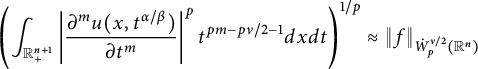 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} \approx\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)} \end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} \approx\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)} \end{align*} $$
with
![]() $p>1,\ \nu \in (0,2)$
and
$p>1,\ \nu \in (0,2)$
and
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x).$
Moreover, we establish fractional logarithmic Gagliardo–Nirenberg inequalities which imply the
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x).$
Moreover, we establish fractional logarithmic Gagliardo–Nirenberg inequalities which imply the
![]() $L^p$
-logarithmic Sobolev inequalities for
$L^p$
-logarithmic Sobolev inequalities for
![]() $\dot {W}^{\nu /2}_{p}(\mathbb R^{n}).$
$\dot {W}^{\nu /2}_{p}(\mathbb R^{n}).$
A direct computation indicates that the inequality (1.6) is invariant under the transform
![]() $\phi (x)=\lambda x+x_{0}$
for
$\phi (x)=\lambda x+x_{0}$
for
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $x_{0}\in \mathbb R^{n}$
, i.e.,
$x_{0}\in \mathbb R^{n}$
, i.e.,
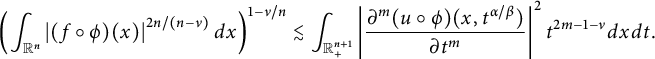 $$ \begin{align*}\left( \int_{\mathbb{R}^n}^{}\left|(f\circ\phi)(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^{m}(u\circ\phi)(x,t^{\alpha/\beta})}{\partial t^m}\right| ^2t^{2m-1-\nu}d{x}d{t}.\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}^n}^{}\left|(f\circ\phi)(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^{m}(u\circ\phi)(x,t^{\alpha/\beta})}{\partial t^m}\right| ^2t^{2m-1-\nu}d{x}d{t}.\end{align*} $$
However, both the Lebesgue space
![]() $L^{2n/(n-\nu )}(\mathbb R^{n})$
with
$L^{2n/(n-\nu )}(\mathbb R^{n})$
with
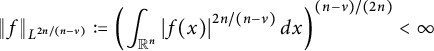 $$ \begin{align*}\|f\|_{L^{2n/(n-\nu)}}:=\left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}<\infty\end{align*} $$
$$ \begin{align*}\|f\|_{L^{2n/(n-\nu)}}:=\left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}<\infty\end{align*} $$
and the Sobolev space
![]() $\dot {H}^{\nu /2}(\mathbb R^{n})$
with
$\dot {H}^{\nu /2}(\mathbb R^{n})$
with
 $$ \begin{align*}\|f\|_{\dot{H}^{\nu/2}(\mathbb R^{n})}&\approx\Bigg(\int_{\mathbb{R}_{+}^{n+1}}\big|\widetilde{\nabla}_{x}^{m}u(x,t^{{\alpha/\beta}})\big|^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\\&\approx \Bigg(\int_{\mathbb{R}_{+}^{n+1}}\left|\frac{\partial^mu(x,t^{{\alpha/\beta}})}{\partial t^m}\right|^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}<\infty\end{align*} $$
$$ \begin{align*}\|f\|_{\dot{H}^{\nu/2}(\mathbb R^{n})}&\approx\Bigg(\int_{\mathbb{R}_{+}^{n+1}}\big|\widetilde{\nabla}_{x}^{m}u(x,t^{{\alpha/\beta}})\big|^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\\&\approx \Bigg(\int_{\mathbb{R}_{+}^{n+1}}\left|\frac{\partial^mu(x,t^{{\alpha/\beta}})}{\partial t^m}\right|^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}<\infty\end{align*} $$
are not invariant under the transform
![]() $\phi $
. In [Reference Xiao39], using the characterization of Q-type space
$\phi $
. In [Reference Xiao39], using the characterization of Q-type space
![]() $Q_{\kappa }(\mathbb R^{n})$
, Xiao obtained a revised conformal invariant Sobolev-type trace inequality (see [Reference Xiao39, Theorem 4.1]). In Theorem 5.4, following the idea of [Reference Xiao39], we prove the local versions of (1.4) for
$Q_{\kappa }(\mathbb R^{n})$
, Xiao obtained a revised conformal invariant Sobolev-type trace inequality (see [Reference Xiao39, Theorem 4.1]). In Theorem 5.4, following the idea of [Reference Xiao39], we prove the local versions of (1.4) for
![]() $f\in Q_{\nu /2}(\mathbb {R}^n)$
with
$f\in Q_{\nu /2}(\mathbb {R}^n)$
with
![]() $\nu \in (0,\min \{ 2, n\})$
and
$\nu \in (0,\min \{ 2, n\})$
and
![]() $u(x,t)=G_{t}^{\alpha ,\beta }*f(x):$
$u(x,t)=G_{t}^{\alpha ,\beta }*f(x):$
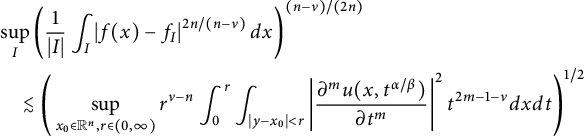 $$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\quad\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\nonumber \end{align} $$
$$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\quad\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\nonumber \end{align} $$
and
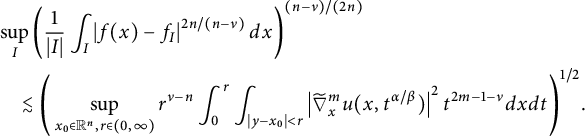 $$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\quad\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\nonumber \end{align} $$
$$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\quad\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\nonumber \end{align} $$
Notations: In this paper,
![]() $A\lesssim B$
means
$A\lesssim B$
means
![]() $A\leq CB$
for a positive constant C.
$A\leq CB$
for a positive constant C.
![]() $A\approx B$
means that
$A\approx B$
means that
![]() $A\lesssim B$
and
$A\lesssim B$
and
![]() $B\lesssim A$
. Let
$B\lesssim A$
. Let
![]() $k \in \mathbb {N}.$
Here,
$k \in \mathbb {N}.$
Here,
![]() $\mathbb {N}$
denotes the set of natural numbers. The symbol
$\mathbb {N}$
denotes the set of natural numbers. The symbol
![]() $C^{k}(\mathbb {R}^n)$
denotes the class of all functions
$C^{k}(\mathbb {R}^n)$
denotes the class of all functions
![]() $f : \mathbb {R}^n \to \mathbb {R}$
with k continuous partial derivatives. Denote by
$f : \mathbb {R}^n \to \mathbb {R}$
with k continuous partial derivatives. Denote by
![]() $f\ast g$
the convolution of functions f and g, i.e.,
$f\ast g$
the convolution of functions f and g, i.e.,
2 Preliminaries
2.1 Basic lemmas
First, we investigate the integrability of the Fourier transform of the time-space fractional heat kernel
![]() $G_{t}^{\alpha , \beta }(\cdot )$
.
$G_{t}^{\alpha , \beta }(\cdot )$
.
Definition 2.1 Let
![]() $\alpha>n/2$
and
$\alpha>n/2$
and
![]() $\beta \in (0,1]$
. We say
$\beta \in (0,1]$
. We say
![]() $G_t^{\alpha ,\beta }(\cdot )$
is the time-space fractional heat kernel if for
$G_t^{\alpha ,\beta }(\cdot )$
is the time-space fractional heat kernel if for
![]() $(x,t)\in \mathbb {R}^n\times (0,\infty )$
,
$(x,t)\in \mathbb {R}^n\times (0,\infty )$
,
where
![]() $g_\beta (\cdot )$
is the density function of
$g_\beta (\cdot )$
is the density function of
![]() $D_1$
and is infinitely differentiable on the entire real line with
$D_1$
and is infinitely differentiable on the entire real line with
![]() $g_\beta (u)=0$
for
$g_\beta (u)=0$
for
![]() $u\leq 0$
( cf. [Reference Foondun and Nane17]) and
$u\leq 0$
( cf. [Reference Foondun and Nane17]) and
![]() $K_{\alpha ,t}(\cdot )$
denotes the fractional heat kernel defined as
$K_{\alpha ,t}(\cdot )$
denotes the fractional heat kernel defined as
It follows from [Reference Foondun and Nane17, (2.5)] that, when
![]() $u\to \infty $
, there holds
$u\to \infty $
, there holds
Following [Reference Foondun and Nane17, p. 8], the Fourier transform of the kernel
![]() $G_t^{\alpha ,\beta }(\cdot )$
can be represented as
$G_t^{\alpha ,\beta }(\cdot )$
can be represented as
where
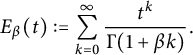 $$ \begin{align} E_\beta(t):=\sum_{k=0}^{\infty}\frac{t^k}{\Gamma(1+\beta k)}. \end{align} $$
$$ \begin{align} E_\beta(t):=\sum_{k=0}^{\infty}\frac{t^k}{\Gamma(1+\beta k)}. \end{align} $$
Here, the symbol
![]() $\Gamma (\cdot )$
denotes the Gamma function and
$\Gamma (\cdot )$
denotes the Gamma function and
![]() $E_{\beta } (\cdot )$
is Mittag-Leffler function.
$E_{\beta } (\cdot )$
is Mittag-Leffler function.
Remark 2.2 In [Reference Foondun and Nane17], the time-space fractional heat kernel
![]() $G_{t}^{\alpha ,\beta }(\cdot )$
is defined by
$G_{t}^{\alpha ,\beta }(\cdot )$
is defined by
where
![]() $\widehat {p(\cdot ,s)}(\xi )=e^{-s|\xi |^{\alpha }}=\widehat {K_{\alpha ,s}}(\xi )$
and
$\widehat {p(\cdot ,s)}(\xi )=e^{-s|\xi |^{\alpha }}=\widehat {K_{\alpha ,s}}(\xi )$
and
By the change of variable:
![]() $u=ts^{-1/\beta }$
, we have
$u=ts^{-1/\beta }$
, we have
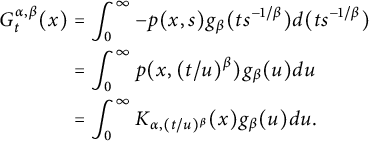 $$ \begin{align*} G_{t}^{\alpha,\beta}(x)&=\int_{0}^{\infty} -p(x,s) g_{\beta}(ts^{-1/\beta}) d(ts^{-1/\beta}) \\ &=\int_{0}^{\infty} p(x,(t/u)^{\beta})g_{\beta}(u)du\\ &=\int_{0}^{\infty} K_{\alpha,(t/u)^{\beta}}(x)g_{\beta}(u)du. \end{align*} $$
$$ \begin{align*} G_{t}^{\alpha,\beta}(x)&=\int_{0}^{\infty} -p(x,s) g_{\beta}(ts^{-1/\beta}) d(ts^{-1/\beta}) \\ &=\int_{0}^{\infty} p(x,(t/u)^{\beta})g_{\beta}(u)du\\ &=\int_{0}^{\infty} K_{\alpha,(t/u)^{\beta}}(x)g_{\beta}(u)du. \end{align*} $$
Thus, we use
![]() $(t/u)^{\beta }$
as the subscript in (2.1). Such a representation of
$(t/u)^{\beta }$
as the subscript in (2.1). Such a representation of
![]() $G_{t}^{\alpha ,\beta }(\cdot )$
was also used by Foondun and Nane [Reference Foondun and Nane17]. Precisely,
$G_{t}^{\alpha ,\beta }(\cdot )$
was also used by Foondun and Nane [Reference Foondun and Nane17]. Precisely,
(see [Reference Foondun and Nane17, p. 502, line 10]).
For
![]() $\alpha =2$
and
$\alpha =2$
and
![]() $\beta =1$
, Foondun and Nane [Reference Foondun and Nane17, p. 501, (2.12)] pointed out that when
$\beta =1$
, Foondun and Nane [Reference Foondun and Nane17, p. 501, (2.12)] pointed out that when
![]() $n=1$
, the kernel
$n=1$
, the kernel
![]() $G^{2,1}_{t}(\cdot )$
becomes
$G^{2,1}_{t}(\cdot )$
becomes
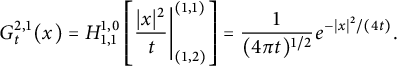 $$ \begin{align*}G^{2,1}_{t}(x)=H^{1,0}_{1,1}\left[ \frac{|x|^{2}}{t}\bigg|_{(1,2)}^{(1,1)} \right]=\frac{1}{(4\pi t)^{1/2}} e^{-{|x|^{2}}/{(4t)}}.\end{align*} $$
$$ \begin{align*}G^{2,1}_{t}(x)=H^{1,0}_{1,1}\left[ \frac{|x|^{2}}{t}\bigg|_{(1,2)}^{(1,1)} \right]=\frac{1}{(4\pi t)^{1/2}} e^{-{|x|^{2}}/{(4t)}}.\end{align*} $$
The cases
![]() $n\geq 2$
are similar. In fact, by (2.2), we have
$n\geq 2$
are similar. In fact, by (2.2), we have
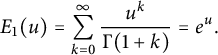 $$ \begin{align*}E_{1}(u)=\sum_{k=0}^{\infty}\frac{u^{k}}{\Gamma(1+ k)} = e^{u}.\end{align*} $$
$$ \begin{align*}E_{1}(u)=\sum_{k=0}^{\infty}\frac{u^{k}}{\Gamma(1+ k)} = e^{u}.\end{align*} $$
Then for
![]() $n\geq 2$
, we can obtain
$n\geq 2$
, we can obtain
 $$ \begin{align*} G_{t}^{2,1}(x)&=\frac{1}{(2\pi)^{n}}\int_{\mathbb{R}^{n}}e^{ix\cdot\xi}E_{1}(-|\xi|^{2}t)d\xi\\ &=\frac{1}{(2\pi)^{n}}\int_{\mathbb{R}^{n}}e^{ix\cdot\xi}e^{-|\xi|^{2}t}d\xi\\ &=\prod_{j=1}^{n}\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{ix_{j}\xi_{j}}E_{1}(-\xi_j^{2}t)d\xi_{j}\\ &=\frac{1}{(4\pi t)^{n/2}} e^{-{|x|^{2}}/{(4t)}}, \end{align*} $$
$$ \begin{align*} G_{t}^{2,1}(x)&=\frac{1}{(2\pi)^{n}}\int_{\mathbb{R}^{n}}e^{ix\cdot\xi}E_{1}(-|\xi|^{2}t)d\xi\\ &=\frac{1}{(2\pi)^{n}}\int_{\mathbb{R}^{n}}e^{ix\cdot\xi}e^{-|\xi|^{2}t}d\xi\\ &=\prod_{j=1}^{n}\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{ix_{j}\xi_{j}}E_{1}(-\xi_j^{2}t)d\xi_{j}\\ &=\frac{1}{(4\pi t)^{n/2}} e^{-{|x|^{2}}/{(4t)}}, \end{align*} $$
which indicates that
![]() $G_{t}^{2,1}(\cdot )$
becomes the classical heat kernel.
$G_{t}^{2,1}(\cdot )$
becomes the classical heat kernel.
Remark 2.3 Let
![]() $\mathcal {L}$
be the Laplace transform, i.e.,
$\mathcal {L}$
be the Laplace transform, i.e.,
After applying the Fourier transform and the Laplace transform to
![]() $G_{t}^{\alpha ,\beta }(\cdot ),$
we have
$G_{t}^{\alpha ,\beta }(\cdot ),$
we have
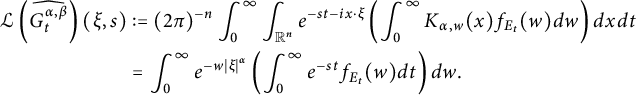 $$ \begin{align*} \mathcal{L}\left(\widehat{G_{t}^{\alpha,\beta}} \right)(\xi,s)&:=(2\pi)^{-n} \int_{0}^{\infty}\int_{\mathbb{R}^{n}} e^{-st-ix\cdot\xi}\left(\int_{0}^{\infty} K_{\alpha,w}(x)f_{E_{t}}(w)dw \right) dxdt\\ &=\int_{0}^{\infty}e^{-w|\xi|^{\alpha}}\left( \int_{0}^{\infty}e^{-st}f_{E_{t}}(w)dt\right)dw. \end{align*} $$
$$ \begin{align*} \mathcal{L}\left(\widehat{G_{t}^{\alpha,\beta}} \right)(\xi,s)&:=(2\pi)^{-n} \int_{0}^{\infty}\int_{\mathbb{R}^{n}} e^{-st-ix\cdot\xi}\left(\int_{0}^{\infty} K_{\alpha,w}(x)f_{E_{t}}(w)dw \right) dxdt\\ &=\int_{0}^{\infty}e^{-w|\xi|^{\alpha}}\left( \int_{0}^{\infty}e^{-st}f_{E_{t}}(w)dt\right)dw. \end{align*} $$
By [Reference Meerschaert and Straka32, p. 3, (2.9) and (2.10)], the Laplace transform
![]() $t\to s$
of
$t\to s$
of
![]() $f_{E_{t}}(w)$
is
$f_{E_{t}}(w)$
is
Then
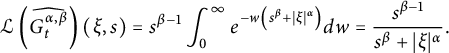 $$ \begin{align*}\mathcal{L}\left(\widehat{G_{t}^{\alpha,\beta}} \right)(\xi,s)= s^{\beta-1}\int_{0}^{\infty}e^{-w\left(s^{\beta}+|\xi|^{\alpha} \right)} dw=\frac{s^{\beta-1}}{s^{\beta}+|\xi|^{\alpha}}. \end{align*} $$
$$ \begin{align*}\mathcal{L}\left(\widehat{G_{t}^{\alpha,\beta}} \right)(\xi,s)= s^{\beta-1}\int_{0}^{\infty}e^{-w\left(s^{\beta}+|\xi|^{\alpha} \right)} dw=\frac{s^{\beta-1}}{s^{\beta}+|\xi|^{\alpha}}. \end{align*} $$
Thus, by the inverse Laplace transform, we can get
Remark 2.4 Applying the Laplace transform to
![]() $\partial ^{\beta }_{t}u(x,t)$
, we have
$\partial ^{\beta }_{t}u(x,t)$
, we have
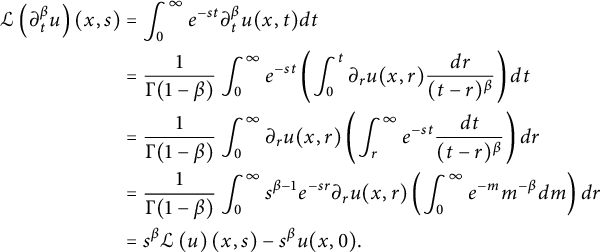 $$ \begin{align*} \mathcal{L}\left(\partial^{\beta}_{t}u \right)(x,s)&=\int_{0}^{\infty}e^{-st}\partial^{\beta}_{t}u(x,t)dt\\ &=\frac{1}{\Gamma(1-\beta)}\int_{0}^{\infty}e^{-st}\left( \int_{0}^{t} \partial_{r}u(x,r)\frac{dr}{(t-r)^{\beta}}\right)dt\\ &=\frac{1}{\Gamma(1-\beta)}\int_{0}^{\infty}\partial_{r}u(x,r)\left( \int_{r}^{\infty}e^{-st} \frac{dt}{(t-r)^{\beta}}\right)dr\\ &=\frac{1}{\Gamma(1-\beta)}\int_{0}^{\infty}s^{\beta-1}e^{-sr}\partial_{r}u(x,r)\left(\int_{0}^{\infty} e^{-m}m^{-\beta}dm \right) dr\\ &= s^{\beta}\mathcal{L}\left( u \right)(x,s)-s^{\beta}u(x,0). \end{align*} $$
$$ \begin{align*} \mathcal{L}\left(\partial^{\beta}_{t}u \right)(x,s)&=\int_{0}^{\infty}e^{-st}\partial^{\beta}_{t}u(x,t)dt\\ &=\frac{1}{\Gamma(1-\beta)}\int_{0}^{\infty}e^{-st}\left( \int_{0}^{t} \partial_{r}u(x,r)\frac{dr}{(t-r)^{\beta}}\right)dt\\ &=\frac{1}{\Gamma(1-\beta)}\int_{0}^{\infty}\partial_{r}u(x,r)\left( \int_{r}^{\infty}e^{-st} \frac{dt}{(t-r)^{\beta}}\right)dr\\ &=\frac{1}{\Gamma(1-\beta)}\int_{0}^{\infty}s^{\beta-1}e^{-sr}\partial_{r}u(x,r)\left(\int_{0}^{\infty} e^{-m}m^{-\beta}dm \right) dr\\ &= s^{\beta}\mathcal{L}\left( u \right)(x,s)-s^{\beta}u(x,0). \end{align*} $$
After applying the Fourier transform and the Laplace transform to (1.1), we can get
which indicates that
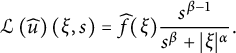 $$ \begin{align*}\mathcal{L}\left( \widehat{u} \right)(\xi,s)=\widehat{f}(\xi)\frac{s^{\beta-1}}{s^{\beta}+|\xi|^{\alpha}}.\end{align*} $$
$$ \begin{align*}\mathcal{L}\left( \widehat{u} \right)(\xi,s)=\widehat{f}(\xi)\frac{s^{\beta-1}}{s^{\beta}+|\xi|^{\alpha}}.\end{align*} $$
Applying the inverse Laplace transform, we obtain
We can use the inverse Fourier transform to deduce that
Thus, the solution to equations (1.1) can be represented as (2.3).
Lemma 2.5 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha> n+m$
and
$\alpha> n+m$
and
![]() $\beta \in (0,1]$
.
$\beta \in (0,1]$
.
-
(i) It holds
(2.4) $$ \begin{align} \begin{cases} \int_{0}^{\infty}|E_\beta(-t)|^2t^\delta dt<\infty,&\qquad\ \ \ -1<\delta<1,\\ \int_{0}^{\infty}\Big|\frac{d{^m}E_\beta(-t)}{d{t^m}}\Big|^2t^{\delta} dt<\infty,&\ -1<\delta<2m+1. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \int_{0}^{\infty}|E_\beta(-t)|^2t^\delta dt<\infty,&\qquad\ \ \ -1<\delta<1,\\ \int_{0}^{\infty}\Big|\frac{d{^m}E_\beta(-t)}{d{t^m}}\Big|^2t^{\delta} dt<\infty,&\ -1<\delta<2m+1. \end{cases} \end{align} $$
-
(ii) If
 $\delta \in (-1,2\alpha -1)$
, there exists a constant
$\delta \in (-1,2\alpha -1)$
, there exists a constant
 $M(n,\alpha ,\beta ,\delta )$
such that
$M(n,\alpha ,\beta ,\delta )$
such that  $$ \begin{align*} \int_{0}^{\infty}\left| \widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)\right|^2 t^{\delta}dt=M(n,\alpha,\beta,\delta)|\xi|^{-\delta-1}.\end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}\left| \widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)\right|^2 t^{\delta}dt=M(n,\alpha,\beta,\delta)|\xi|^{-\delta-1}.\end{align*} $$
-
(iii) If
 $\delta \in (2m-1,2m+2\alpha -1)$
,
$\delta \in (2m-1,2m+2\alpha -1)$
,
 $m\in \mathbb {Z}_+$
and
$m\in \mathbb {Z}_+$
and
 $\alpha>m$
, then
$\alpha>m$
, then  $$ \begin{align*}\int_{0}^{\infty} \left| \frac{\partial^m\widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)}{\partial t^m}\right|^2 t^{\delta}dt\approx|\xi|^{2m-\delta-1}.\end{align*} $$
$$ \begin{align*}\int_{0}^{\infty} \left| \frac{\partial^m\widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)}{\partial t^m}\right|^2 t^{\delta}dt\approx|\xi|^{2m-\delta-1}.\end{align*} $$
Proof It follows from [Reference Foondun and Nane17, (2.7)] that for
![]() $t>0$
,
$t>0$
,
Assume that
![]() $-1< {\delta }<1$
. Then
$-1< {\delta }<1$
. Then
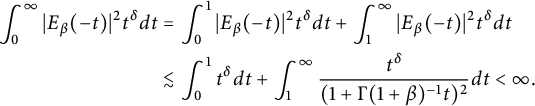 $$ \begin{align*} \int_{0}^{\infty}|E_\beta(-t)|^2t^{\delta} d{t}&=\int_{0}^{1}|E_\beta(-t)|^2t^{\delta} d{t}+\int_{1}^{\infty}|E_\beta(-t)|^2t^{\delta} d{t}\\ &\lesssim \int_{0}^{1}t^{\delta}d{t}+\int_{1}^{\infty}\frac{t^{\delta}}{(1+\Gamma(1+\beta)^{-1}t)^2}d{t}<\infty. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}|E_\beta(-t)|^2t^{\delta} d{t}&=\int_{0}^{1}|E_\beta(-t)|^2t^{\delta} d{t}+\int_{1}^{\infty}|E_\beta(-t)|^2t^{\delta} d{t}\\ &\lesssim \int_{0}^{1}t^{\delta}d{t}+\int_{1}^{\infty}\frac{t^{\delta}}{(1+\Gamma(1+\beta)^{-1}t)^2}d{t}<\infty. \end{align*} $$
Following Haubold, Mathai, and Saxena [Reference Haubold, Mathai and Saxena22], as
![]() $t\to \infty ,$
for
$t\to \infty ,$
for
![]() $M\in \mathbb {N}_{+}$
, we have
$M\in \mathbb {N}_{+}$
, we have
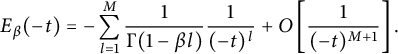 $$ \begin{align} E_\beta(-t)&= -\sum_{l=1}^{M}\frac{1}{\Gamma(1-\beta l)}\frac{1}{(-t)^l}+O\left[ \frac{1}{(-t)^{M+1}}\right]. \end{align} $$
$$ \begin{align} E_\beta(-t)&= -\sum_{l=1}^{M}\frac{1}{\Gamma(1-\beta l)}\frac{1}{(-t)^l}+O\left[ \frac{1}{(-t)^{M+1}}\right]. \end{align} $$
Then
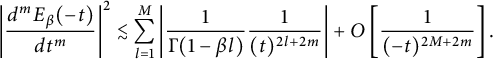 $$ \begin{align*} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2 &\lesssim \sum_{l=1}^{M}\left| \frac{1}{\Gamma(1-\beta l)}\frac{1}{(t)^{2l+2m}}\right|+ O\left[ \frac{1}{(-t)^{2M+2m}}\right]. \end{align*} $$
$$ \begin{align*} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2 &\lesssim \sum_{l=1}^{M}\left| \frac{1}{\Gamma(1-\beta l)}\frac{1}{(t)^{2l+2m}}\right|+ O\left[ \frac{1}{(-t)^{2M+2m}}\right]. \end{align*} $$
There exists a constant
![]() $A_\beta $
for t in a neighborhood of
$A_\beta $
for t in a neighborhood of
![]() $0$
such that
$0$
such that
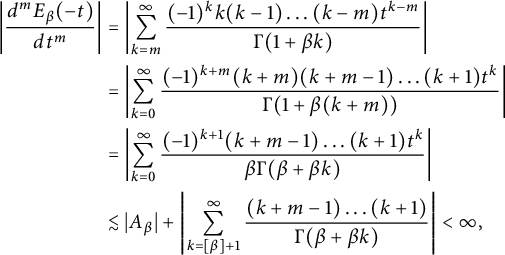 $$ \begin{align} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right| &=\left| \sum_{k=m}^{\infty}\frac{(-1)^kk(k-1)\dots(k-m)t^{k-m}}{\Gamma(1+\beta k)}\right| \\ &=\left| \sum_{k=0}^{\infty}\frac{(-1)^{k+m}(k+m)(k+m-1)\dots(k+1)t^k}{\Gamma(1+\beta(k+m))}\right| \notag\\ &=\left| \sum_{k=0}^{\infty}\frac{(-1)^{k+1}(k+m-1)\dots(k+1)t^k}{\beta\Gamma(\beta+\beta k)}\right| \notag\\ &\lesssim |A_\beta|+\left| \sum_{k=[\beta]+1}^{\infty}\frac{(k+m-1)\dots(k+1)}{\Gamma(\beta+\beta k)}\right|<\infty,\notag \end{align} $$
$$ \begin{align} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right| &=\left| \sum_{k=m}^{\infty}\frac{(-1)^kk(k-1)\dots(k-m)t^{k-m}}{\Gamma(1+\beta k)}\right| \\ &=\left| \sum_{k=0}^{\infty}\frac{(-1)^{k+m}(k+m)(k+m-1)\dots(k+1)t^k}{\Gamma(1+\beta(k+m))}\right| \notag\\ &=\left| \sum_{k=0}^{\infty}\frac{(-1)^{k+1}(k+m-1)\dots(k+1)t^k}{\beta\Gamma(\beta+\beta k)}\right| \notag\\ &\lesssim |A_\beta|+\left| \sum_{k=[\beta]+1}^{\infty}\frac{(k+m-1)\dots(k+1)}{\Gamma(\beta+\beta k)}\right|<\infty,\notag \end{align} $$
which indicates that when
![]() $-1<{\delta }<2m+1$
,
$-1<{\delta }<2m+1$
,
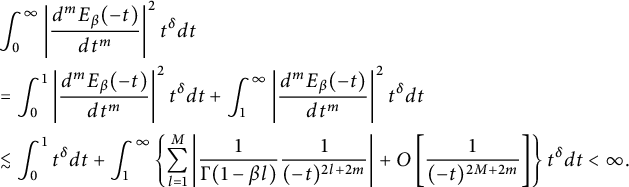 $$ \begin{align*} &\int_{0}^{\infty} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2t^{\delta} d{t}\notag\\ &= \int_{0}^{1} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2t^{\delta} d{t}+\int_{1}^{\infty} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2t^{\delta} d{t}\notag\\ &\lesssim \int_{0}^{1}t^{\delta} d{t}+\int_{1}^{\infty}\left\{\sum_{l=1}^{M}\left| \frac{1}{\Gamma(1-\beta l)}\frac{1}{(-t)^{2l+2m}}\right|+ O\left[ \frac{1}{(-t)^{2M+2m}}\right]\right\}t^{\delta} d{t} <\infty\notag. \end{align*} $$
$$ \begin{align*} &\int_{0}^{\infty} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2t^{\delta} d{t}\notag\\ &= \int_{0}^{1} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2t^{\delta} d{t}+\int_{1}^{\infty} \left| \frac{d{^m}E_\beta(-t)}{d{t^m}}\right|^2t^{\delta} d{t}\notag\\ &\lesssim \int_{0}^{1}t^{\delta} d{t}+\int_{1}^{\infty}\left\{\sum_{l=1}^{M}\left| \frac{1}{\Gamma(1-\beta l)}\frac{1}{(-t)^{2l+2m}}\right|+ O\left[ \frac{1}{(-t)^{2M+2m}}\right]\right\}t^{\delta} d{t} <\infty\notag. \end{align*} $$
(ii) For
![]() ${\delta }\in (-1,2\alpha -1)$
, by the change of variable
${\delta }\in (-1,2\alpha -1)$
, by the change of variable
![]() $u=|\xi |^\alpha t^\alpha $
, we can obtain
$u=|\xi |^\alpha t^\alpha $
, we can obtain
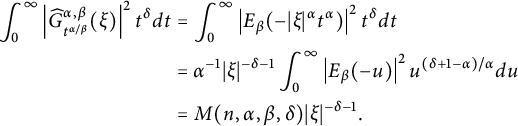 $$ \begin{align*} \int_{0}^{\infty}\left| \widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)\right|^2 t^{\delta} d{t}&=\int_{0}^{\infty}\left| E_\beta(-|\xi|^\alpha t^\alpha)\right| ^2t^{\delta} dt\\ &=\alpha^{-1}|\xi|^{-{\delta}-1}\int_{0}^{\infty}\left| E_\beta(-u)\right| ^2u^{({\delta}+1-\alpha)/\alpha}d{u}\\ &=M(n,\alpha,\beta,{\delta})|\xi|^{-{\delta}-1}. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}\left| \widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)\right|^2 t^{\delta} d{t}&=\int_{0}^{\infty}\left| E_\beta(-|\xi|^\alpha t^\alpha)\right| ^2t^{\delta} dt\\ &=\alpha^{-1}|\xi|^{-{\delta}-1}\int_{0}^{\infty}\left| E_\beta(-u)\right| ^2u^{({\delta}+1-\alpha)/\alpha}d{u}\\ &=M(n,\alpha,\beta,{\delta})|\xi|^{-{\delta}-1}. \end{align*} $$
(iii) Notice that
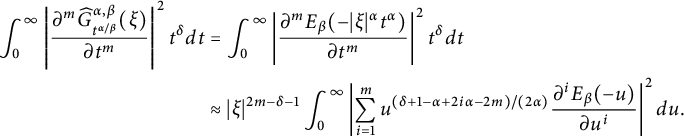 $$ \begin{align*} \int_{0}^{\infty}\left|\frac{\partial^m\widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)}{\partial t^m} \right|^2 t^{\delta} d{t}&=\int_{0}^{\infty}\left|\frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m} \right| ^2t^{\delta} dt\\ &\approx |\xi|^{2m-{\delta}-1}\int_{0}^{\infty}\left|\sum_{i=1}^m u^{({\delta}+1-\alpha+2i\alpha-2m)/(2\alpha)}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right| ^2d{u}. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}\left|\frac{\partial^m\widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)}{\partial t^m} \right|^2 t^{\delta} d{t}&=\int_{0}^{\infty}\left|\frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m} \right| ^2t^{\delta} dt\\ &\approx |\xi|^{2m-{\delta}-1}\int_{0}^{\infty}\left|\sum_{i=1}^m u^{({\delta}+1-\alpha+2i\alpha-2m)/(2\alpha)}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right| ^2d{u}. \end{align*} $$
For
![]() ${\delta } \in (2m-1,2\alpha +2m-1)$
and
${\delta } \in (2m-1,2\alpha +2m-1)$
and
![]() $m\in \mathbb {Z}_+$
, (2.4) implies
$m\in \mathbb {Z}_+$
, (2.4) implies
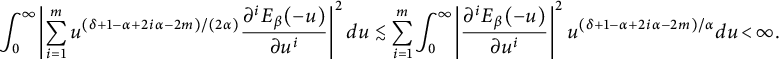 $$ \begin{align*}\int_{0}^{\kern-1pt\infty}\kern-1.2pt\left|\sum_{i=1}^m u^{({\delta}+1-\alpha+2i\alpha-2m)/(2\alpha)}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right| ^2d{u}\lesssim \sum_{i=1}^m\kern-1.2pt\int_{0}^{\kern-1pt\infty}\kern-1.2pt\left| \frac{\partial^iE_\beta(-u)}{\partial u^i}\right| ^2u^{({\delta}+1-\alpha+2i\alpha-2m)/\alpha}d{u}\kern1.2pt{<}\kern1.2pt\infty.\end{align*} $$
$$ \begin{align*}\int_{0}^{\kern-1pt\infty}\kern-1.2pt\left|\sum_{i=1}^m u^{({\delta}+1-\alpha+2i\alpha-2m)/(2\alpha)}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right| ^2d{u}\lesssim \sum_{i=1}^m\kern-1.2pt\int_{0}^{\kern-1pt\infty}\kern-1.2pt\left| \frac{\partial^iE_\beta(-u)}{\partial u^i}\right| ^2u^{({\delta}+1-\alpha+2i\alpha-2m)/\alpha}d{u}\kern1.2pt{<}\kern1.2pt\infty.\end{align*} $$
Then
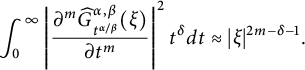 $$ \begin{align*} \int_{0}^{\infty}\left|\frac{\partial^m\widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)}{\partial t^m} \right|^2 t^{\delta} d{t}\approx|\xi|^{2m-{\delta}-1}. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}\left|\frac{\partial^m\widehat{G}_{t^{\alpha/\beta}}^{\alpha,\beta}(\xi)}{\partial t^m} \right|^2 t^{\delta} d{t}\approx|\xi|^{2m-{\delta}-1}. \end{align*} $$
This proves (2.5).
Denote by
![]() $\mathcal M$
the Hardy–Littlewood maximal operator, i.e.,
$\mathcal M$
the Hardy–Littlewood maximal operator, i.e.,
Lemma 2.6 For
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha> 1/2$
and
$\alpha> 1/2$
and
![]() $\beta \in (0,1]$
, there exists a constant C depending only on n,
$\beta \in (0,1]$
, there exists a constant C depending only on n,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that for
$\beta $
such that for
![]() $ x, y \in \mathbb {R}^n$
and
$ x, y \in \mathbb {R}^n$
and
![]() $ f\in C_0^\infty (\mathbb {R}^n)$
,
$ f\in C_0^\infty (\mathbb {R}^n)$
,
Proof Let
![]() $f_{t,\alpha ,\beta }(x):=f(t^{\beta /\alpha }x)$
. For any ball
$f_{t,\alpha ,\beta }(x):=f(t^{\beta /\alpha }x)$
. For any ball
![]() $B\subset \mathbb {R}^n$
centered at
$B\subset \mathbb {R}^n$
centered at
![]() $x_B$
with radius
$x_B$
with radius
![]() $r_B$
, define
$r_B$
, define
![]() $B_{t,\alpha ,\beta }$
as
$B_{t,\alpha ,\beta }$
as
![]() $B_{t,\alpha ,\beta }:=B(t^{\beta /\alpha }x_B,t^{\beta /\alpha }r_B)$
. If
$B_{t,\alpha ,\beta }:=B(t^{\beta /\alpha }x_B,t^{\beta /\alpha }r_B)$
. If
![]() $x\in B$
, then
$x\in B$
, then
![]() $t^{\beta /\alpha }x\in B_{t,\alpha ,\beta }$
. Hence, it is easy to see that
$t^{\beta /\alpha }x\in B_{t,\alpha ,\beta }$
. Hence, it is easy to see that
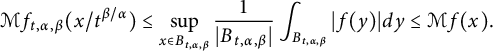 $$ \begin{align} \mathcal{M}f_{t,\alpha,\beta}(x/t^{\beta/\alpha})\leq \sup_{x\in B_{t,\alpha,\beta}}\frac{1}{|B_{t,\alpha,\beta}|}\int_{B_{t,\alpha,\beta}}|f(y)|dy\leq \mathcal{M}f(x). \end{align} $$
$$ \begin{align} \mathcal{M}f_{t,\alpha,\beta}(x/t^{\beta/\alpha})\leq \sup_{x\in B_{t,\alpha,\beta}}\frac{1}{|B_{t,\alpha,\beta}|}\int_{B_{t,\alpha,\beta}}|f(y)|dy\leq \mathcal{M}f(x). \end{align} $$
We only need to prove
In fact, if (2.8) holds, (2.7) and the change of variable
![]() $z=t^{\alpha /\beta }u$
give
$z=t^{\alpha /\beta }u$
give
 $$ \begin{align*} |G_t^{\alpha,\beta}\ast f(x-y)|&\approx\left| \int_{\mathbb{R}^n}\frac{t^\beta}{(t^{\beta/\alpha}+|x-y-z|)^{n+\alpha}}f(z)d{z} \right|\notag\\ &\approx\left| \int_{\mathbb{R}^n}t^{-n{\beta/\alpha}}\frac{1}{(1+|\frac{x-y}{t^{\beta/\alpha}}-u|)^{n+\alpha}} f(t^{\beta/\alpha}u)t^{n{\beta/\alpha}}d{u}\right|\notag\\ &\lesssim(1+|y|/t^{\beta/\alpha})^n\mathcal{M}f_{t,\alpha,\beta}({x}/{t^{\beta/\alpha}})\notag\\ &\lesssim(1+|y|/t^{\beta/\alpha})^n\mathcal{M}f(x). \end{align*} $$
$$ \begin{align*} |G_t^{\alpha,\beta}\ast f(x-y)|&\approx\left| \int_{\mathbb{R}^n}\frac{t^\beta}{(t^{\beta/\alpha}+|x-y-z|)^{n+\alpha}}f(z)d{z} \right|\notag\\ &\approx\left| \int_{\mathbb{R}^n}t^{-n{\beta/\alpha}}\frac{1}{(1+|\frac{x-y}{t^{\beta/\alpha}}-u|)^{n+\alpha}} f(t^{\beta/\alpha}u)t^{n{\beta/\alpha}}d{u}\right|\notag\\ &\lesssim(1+|y|/t^{\beta/\alpha})^n\mathcal{M}f_{t,\alpha,\beta}({x}/{t^{\beta/\alpha}})\notag\\ &\lesssim(1+|y|/t^{\beta/\alpha})^n\mathcal{M}f(x). \end{align*} $$
Below, we prove (2.8). If
![]() $|x|<|y|$
, it is obvious that
$|x|<|y|$
, it is obvious that
![]() $G_1^{\alpha ,\beta }(x-y)<1$
. On the other hand, for
$G_1^{\alpha ,\beta }(x-y)<1$
. On the other hand, for
![]() $|x|\geq |y|$
, it can be deduced from the triangle inequality that
$|x|\geq |y|$
, it can be deduced from the triangle inequality that
Set the decreasing radial majorant function of
![]() $G_1^{\alpha ,\beta }(x-y)$
as
$G_1^{\alpha ,\beta }(x-y)$
as
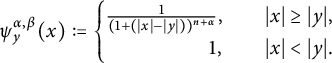 $$ \begin{align*}\psi^{\alpha,\beta}_y(x):= \begin{cases} \frac{1}{(1+(|x|-|y|))^{n+\alpha}},&\quad |x|\geq|y|, \\ \qquad\qquad\quad 1,&\quad |x|<|y|. \end{cases} \end{align*} $$
$$ \begin{align*}\psi^{\alpha,\beta}_y(x):= \begin{cases} \frac{1}{(1+(|x|-|y|))^{n+\alpha}},&\quad |x|\geq|y|, \\ \qquad\qquad\quad 1,&\quad |x|<|y|. \end{cases} \end{align*} $$
With a slight abuse of notation, let us write
![]() $\psi ^{\alpha ,\beta }_y(x)=\psi ^{\alpha ,\beta }_y(r)$
if
$\psi ^{\alpha ,\beta }_y(x)=\psi ^{\alpha ,\beta }_y(r)$
if
![]() $|x|=r$
. We can get
$|x|=r$
. We can get
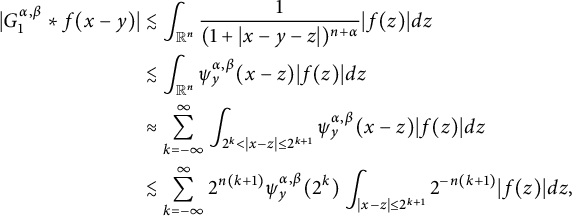 $$ \begin{align*} |G_1^{\alpha,\beta}*f(x-y)|&\lesssim\int_{\mathbb{R}^n}\frac{1}{(1+|x-y-z|)^{n+\alpha}}|f(z)|d{z}\\ &\lesssim\int_{\mathbb{R}^n}\psi^{\alpha,\beta}_y(x-z)|f(z)|d{z}\\ &\approx\sum_{k=-\infty}^{\infty}\int_{2^k<|x-z|\leq2^{k+1}}\psi^{\alpha,\beta}_{y}(x-z)|f(z)|d{z}\\ &\lesssim\sum_{k=-\infty}^{\infty}2^{n(k+1)}\psi^{\alpha,\beta}_y(2^k)\int_{|x-z|\leq2^{k+1}}2^{-n(k+1)}|f(z)|d{z}, \end{align*} $$
$$ \begin{align*} |G_1^{\alpha,\beta}*f(x-y)|&\lesssim\int_{\mathbb{R}^n}\frac{1}{(1+|x-y-z|)^{n+\alpha}}|f(z)|d{z}\\ &\lesssim\int_{\mathbb{R}^n}\psi^{\alpha,\beta}_y(x-z)|f(z)|d{z}\\ &\approx\sum_{k=-\infty}^{\infty}\int_{2^k<|x-z|\leq2^{k+1}}\psi^{\alpha,\beta}_{y}(x-z)|f(z)|d{z}\\ &\lesssim\sum_{k=-\infty}^{\infty}2^{n(k+1)}\psi^{\alpha,\beta}_y(2^k)\int_{|x-z|\leq2^{k+1}}2^{-n(k+1)}|f(z)|d{z}, \end{align*} $$
which, together with the inequality:
implies that
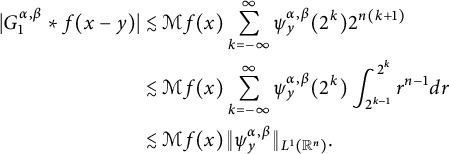 $$ \begin{align*} |G_1^{\alpha,\beta}*f(x-y)|&\lesssim \mathcal{M}f(x)\sum_{k=-\infty}^\infty\psi_y^{\alpha,\beta}(2^k)2^{n(k+1)}\notag\\ &\lesssim \mathcal{M}f(x)\sum_{k=-\infty}^\infty\psi_y^{\alpha,\beta}(2^k)\int_{2^{k-1}}^{2^k}r^{n-1}d{r}\notag\\ &\lesssim \mathcal{M}f(x)\|\psi_y^{\alpha,\beta}\|_{L^1(\mathbb{R}^n)}.\notag \end{align*} $$
$$ \begin{align*} |G_1^{\alpha,\beta}*f(x-y)|&\lesssim \mathcal{M}f(x)\sum_{k=-\infty}^\infty\psi_y^{\alpha,\beta}(2^k)2^{n(k+1)}\notag\\ &\lesssim \mathcal{M}f(x)\sum_{k=-\infty}^\infty\psi_y^{\alpha,\beta}(2^k)\int_{2^{k-1}}^{2^k}r^{n-1}d{r}\notag\\ &\lesssim \mathcal{M}f(x)\|\psi_y^{\alpha,\beta}\|_{L^1(\mathbb{R}^n)}.\notag \end{align*} $$
It follows from a direct computation that
Then we use the change of variable:
![]() $|x|-|y|=r$
to deduce that
$|x|-|y|=r$
to deduce that
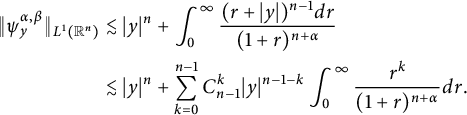 $$ \begin{align*} \|\psi_y^{\alpha,\beta}\|_{L^{1}(\mathbb R^{n})}&\lesssim |y|^n+\int_{0}^{\infty}\frac{(r+|y|)^{n-1}d{r}}{(1+r)^{n+\alpha}}\notag\\ &\lesssim |y|^n+\sum_{k=0}^{n-1} C_{n-1}^{k}|y|^{n-1-k}\int_{0}^{\infty}\frac{r^k}{(1+r)^{n+\alpha}}d{r}. \end{align*} $$
$$ \begin{align*} \|\psi_y^{\alpha,\beta}\|_{L^{1}(\mathbb R^{n})}&\lesssim |y|^n+\int_{0}^{\infty}\frac{(r+|y|)^{n-1}d{r}}{(1+r)^{n+\alpha}}\notag\\ &\lesssim |y|^n+\sum_{k=0}^{n-1} C_{n-1}^{k}|y|^{n-1-k}\int_{0}^{\infty}\frac{r^k}{(1+r)^{n+\alpha}}d{r}. \end{align*} $$
Here,
![]() $C_{n-1}^k$
denotes the number of combinations of choosing k many objects from a group of
$C_{n-1}^k$
denotes the number of combinations of choosing k many objects from a group of
![]() $n-1$
many objects. Notice that
$n-1$
many objects. Notice that
![]() $k\leq n-1$
and
$k\leq n-1$
and
![]() $n+\alpha -k\geq \alpha +1>1$
. There exists
$n+\alpha -k\geq \alpha +1>1$
. There exists
![]() $A>0$
such that
$A>0$
such that
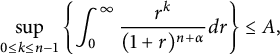 $$ \begin{align*}\sup_{0\leq k\leq n-1}\left\lbrace \int_{0}^{\infty}\frac{r^k}{(1+r)^{n+\alpha}}d{r}\notag\right\rbrace\leq A,\end{align*} $$
$$ \begin{align*}\sup_{0\leq k\leq n-1}\left\lbrace \int_{0}^{\infty}\frac{r^k}{(1+r)^{n+\alpha}}d{r}\notag\right\rbrace\leq A,\end{align*} $$
which makes
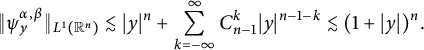 $$ \begin{align*} \|\psi_y^{\alpha,\beta}\|_{L^{1}(\mathbb R^{n})}&\lesssim |y|^n+\sum_{k=-\infty}^\infty C_{n-1}^{k}|y|^{n-1-k} \lesssim (1+|y|)^n.\\[-45pt] \end{align*} $$
$$ \begin{align*} \|\psi_y^{\alpha,\beta}\|_{L^{1}(\mathbb R^{n})}&\lesssim |y|^n+\sum_{k=-\infty}^\infty C_{n-1}^{k}|y|^{n-1-k} \lesssim (1+|y|)^n.\\[-45pt] \end{align*} $$
Lemma 2.7 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha> 1/2$
and
$\alpha> 1/2$
and
![]() $\beta \in (0,1]$
. There exists a constant C depending only on n,
$\beta \in (0,1]$
. There exists a constant C depending only on n,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that for
$\beta $
such that for
![]() $ x, y \in \mathbb {R}^n$
and
$ x, y \in \mathbb {R}^n$
and
![]() $ f\in C_0^\infty (\mathbb {R}^n)$
,
$ f\in C_0^\infty (\mathbb {R}^n)$
,
Proof Let
![]() $f_{t}(x):=f(tx)$
. For any ball
$f_{t}(x):=f(tx)$
. For any ball
![]() $B\subset \mathbb {R}^n$
centered at
$B\subset \mathbb {R}^n$
centered at
![]() $x_B$
with radius
$x_B$
with radius
![]() $r_B$
, denote by
$r_B$
, denote by
![]() $B_{t}$
the ball
$B_{t}$
the ball
![]() $B(tx_B,tr_B)$
. If
$B(tx_B,tr_B)$
. If
![]() $x\in B$
, then
$x\in B$
, then
![]() $tx\in B_{t}$
. Hence, it is easy to see that
$tx\in B_{t}$
. Hence, it is easy to see that
By (2.8) and (2.9), we can obtain
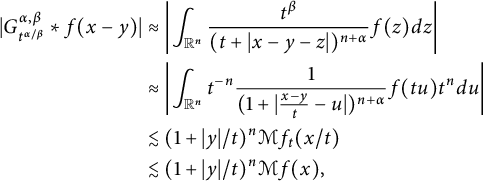 $$ \begin{align*} |G_{t^{\alpha/\beta}}^{\alpha,\beta}\ast f(x-y)|&\approx \left| \int_{\mathbb{R}^n}\frac{t^\beta}{(t+|x-y-z|)^{n+\alpha}}f(z)d{z} \right|\\ &\approx \left| \int_{\mathbb{R}^n}t^{-n}\frac{1}{(1+|\frac{x-y}{t}-u|)^{n+\alpha}} f(tu)t^{n}d{u}\right|\\ &\lesssim (1+|y|/t)^n\mathcal{M}f_{t}({x}/{t})\\ &\lesssim (1+|y|/t)^n\mathcal{M}f(x), \end{align*} $$
$$ \begin{align*} |G_{t^{\alpha/\beta}}^{\alpha,\beta}\ast f(x-y)|&\approx \left| \int_{\mathbb{R}^n}\frac{t^\beta}{(t+|x-y-z|)^{n+\alpha}}f(z)d{z} \right|\\ &\approx \left| \int_{\mathbb{R}^n}t^{-n}\frac{1}{(1+|\frac{x-y}{t}-u|)^{n+\alpha}} f(tu)t^{n}d{u}\right|\\ &\lesssim (1+|y|/t)^n\mathcal{M}f_{t}({x}/{t})\\ &\lesssim (1+|y|/t)^n\mathcal{M}f(x), \end{align*} $$
which indicates Lemma 2.7.
2.2 Regularity of time-space fractional heat kernels
For
![]() $m\in \mathbb {Z}_+$
, define
$m\in \mathbb {Z}_+$
, define
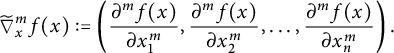 $$ \begin{align*}\widetilde{\nabla}_{x}^mf(x):=\left( \frac{\partial^mf(x)}{\partial x_1^m} , \frac{\partial^mf(x)}{\partial x_2^m},\ldots, \frac{\partial^mf(x)}{\partial x_n^m}\right).\end{align*} $$
$$ \begin{align*}\widetilde{\nabla}_{x}^mf(x):=\left( \frac{\partial^mf(x)}{\partial x_1^m} , \frac{\partial^mf(x)}{\partial x_2^m},\ldots, \frac{\partial^mf(x)}{\partial x_n^m}\right).\end{align*} $$
Lemma 2.8 Let
![]() $\alpha>1/2$
,
$\alpha>1/2$
,
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $x \in \mathbb {R}^n$
and
$x \in \mathbb {R}^n$
and
![]() $t>0$
.
$t>0$
.
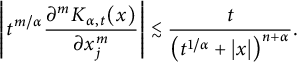 $$ \begin{align*}\left| t^{m/\alpha}\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim\frac{t}{\left( t^{1/\alpha}+|x|\right) ^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left| t^{m/\alpha}\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim\frac{t}{\left( t^{1/\alpha}+|x|\right) ^{n+\alpha}}.\end{align*} $$
Proof The subordinative formula [Reference Grigor’yan19, (5.31)] indicates that
![]() $K_{\alpha ,t}(\cdot )$
can be expressed as
$K_{\alpha ,t}(\cdot )$
can be expressed as
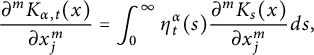 $$ \begin{align*}\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}=\int_{0}^{\infty} \eta_t^\alpha(s) \frac{\partial^mK_s(x)}{\partial x_j^m}ds,\end{align*} $$
$$ \begin{align*}\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}=\int_{0}^{\infty} \eta_t^\alpha(s) \frac{\partial^mK_s(x)}{\partial x_j^m}ds,\end{align*} $$
where
![]() $K_s(\cdot )$
denotes the integral kernel of the heat semigroup
$K_s(\cdot )$
denotes the integral kernel of the heat semigroup
![]() $\{e^{-s(-\Delta _x)}\}_{s>0}$
. Here, the nonnegative continuous function
$\{e^{-s(-\Delta _x)}\}_{s>0}$
. Here, the nonnegative continuous function
![]() $\eta _t^\alpha (\cdot )$
satisfies
$\eta _t^\alpha (\cdot )$
satisfies
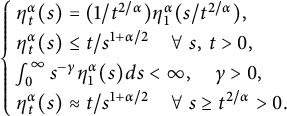 $$ \begin{align} \begin{cases} & \hspace{-8pt}\eta_t^\alpha(s)=(1/t^{2/\alpha})\eta_1^\alpha(s/t^{2/\alpha}),\\& \hspace{-8pt}\eta_t^\alpha(s)\leq t/s^{1+\alpha/2}\quad \forall\ s,\, t>0,\\& \hspace{-8pt}\int_{0}^{\infty}s^{-\gamma}\eta_1^\alpha(s)ds<\infty,\quad \gamma>0,\\& \hspace{-8pt}\eta_t^\alpha(s)\approx t/s^{1+\alpha/2}\quad \forall\ s\geq t^{2/\alpha}>0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} & \hspace{-8pt}\eta_t^\alpha(s)=(1/t^{2/\alpha})\eta_1^\alpha(s/t^{2/\alpha}),\\& \hspace{-8pt}\eta_t^\alpha(s)\leq t/s^{1+\alpha/2}\quad \forall\ s,\, t>0,\\& \hspace{-8pt}\int_{0}^{\infty}s^{-\gamma}\eta_1^\alpha(s)ds<\infty,\quad \gamma>0,\\& \hspace{-8pt}\eta_t^\alpha(s)\approx t/s^{1+\alpha/2}\quad \forall\ s\geq t^{2/\alpha}>0. \end{cases} \end{align} $$
When m is odd, we can get
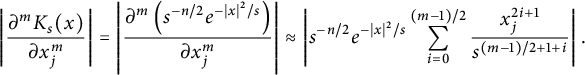 $$ \begin{align*} \left| \frac{\partial^mK_s(x)}{\partial x_j^m}\right| = \left| \frac{\partial^m\left(s^{-n/2}e^{-|x|^2/s}\right)}{\partial x_j^m} \right| \approx \left| s^{-n/2}e^{-|x|^2/s}\sum_{i=0}^{(m-1)/2}\frac{x_j^{2i+1}}{s^{(m-1)/2+1+i}}\right|. \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mK_s(x)}{\partial x_j^m}\right| = \left| \frac{\partial^m\left(s^{-n/2}e^{-|x|^2/s}\right)}{\partial x_j^m} \right| \approx \left| s^{-n/2}e^{-|x|^2/s}\sum_{i=0}^{(m-1)/2}\frac{x_j^{2i+1}}{s^{(m-1)/2+1+i}}\right|. \end{align*} $$
Then
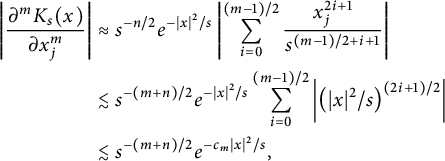 $$ \begin{align*} \left| \frac{\partial^mK_s(x)}{\partial x_j^m} \right|&\approx s^{-n/2}e^{-|x|^2/s} \left| \sum_{i=0}^{(m-1)/2}\frac{x^{2i+1}_j}{s^{(m-1)/2+i+1}}\right| \\ &\lesssim s^{-(m+n)/2}e^{-|x|^2/s}\sum_{i=0}^{(m-1)/2}\left| \left( |x|^2/s\right) ^{(2i+1)/2}\right| \\ &\lesssim s^{-(m+n)/2}e^{-c_m|x|^2/s}, \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mK_s(x)}{\partial x_j^m} \right|&\approx s^{-n/2}e^{-|x|^2/s} \left| \sum_{i=0}^{(m-1)/2}\frac{x^{2i+1}_j}{s^{(m-1)/2+i+1}}\right| \\ &\lesssim s^{-(m+n)/2}e^{-|x|^2/s}\sum_{i=0}^{(m-1)/2}\left| \left( |x|^2/s\right) ^{(2i+1)/2}\right| \\ &\lesssim s^{-(m+n)/2}e^{-c_m|x|^2/s}, \end{align*} $$
where
![]() $c_m$
is a constant depending on m.
$c_m$
is a constant depending on m.
When m is even, we have
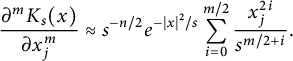 $$ \begin{align*} \frac{\partial^mK_s(x)}{\partial x_j^m}&\approx s^{-n/2}e^{-|x|^2/s}\sum_{i=0}^{m/2}\frac{x_j^{2i}}{s^{m/2+i}}. \end{align*} $$
$$ \begin{align*} \frac{\partial^mK_s(x)}{\partial x_j^m}&\approx s^{-n/2}e^{-|x|^2/s}\sum_{i=0}^{m/2}\frac{x_j^{2i}}{s^{m/2+i}}. \end{align*} $$
For this case, we can obtain
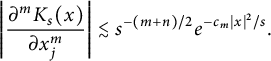 $$ \begin{align*} \left| \frac{\partial^mK_s(x)}{\partial x_j^m}\right| \lesssim s^{-(m+n)/2}e^{-c_m|x|^2/s}.\notag \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mK_s(x)}{\partial x_j^m}\right| \lesssim s^{-(m+n)/2}e^{-c_m|x|^2/s}.\notag \end{align*} $$
Then letting
![]() $m\in \mathbb {Z}_+,$
we can get
$m\in \mathbb {Z}_+,$
we can get
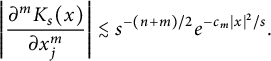 $$ \begin{align} \left| \frac{\partial^mK_s(x)}{\partial x_j^m}\right| \lesssim s^{-(n+m)/2}e^{-c_m|x|^2/s}. \end{align} $$
$$ \begin{align} \left| \frac{\partial^mK_s(x)}{\partial x_j^m}\right| \lesssim s^{-(n+m)/2}e^{-c_m|x|^2/s}. \end{align} $$
By
![]() $s=t^{2/\alpha }h$
, (2.10) and (2.11) imply
$s=t^{2/\alpha }h$
, (2.10) and (2.11) imply
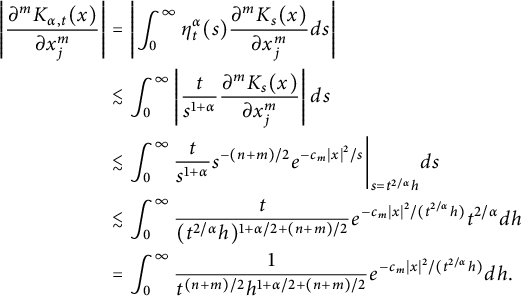 $$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right|&=\left| \int_{0}^{\infty}\eta_t^{\alpha}(s)\frac{\partial^mK_s(x)}{\partial x_j^m}ds\right| \\ &\lesssim\int_{0}^{\infty}\left| \frac{t}{s^{1+\alpha}}\frac{\partial^mK_s(x)}{\partial x_j^m}\right| ds\\ &\lesssim\int_{0}^{\infty}\frac{t}{s^{1+\alpha}} s^{-(n+m)/2}e^{-c_m|x|^2/s}\bigg|_{s=t^{2/\alpha}h}ds\\ &\lesssim\int_{0}^{\infty}\frac{t}{(t^{2/\alpha}h)^{1+\alpha/2+(n+m)/2}}e^{-c_m|x|^2/(t^{2/\alpha}h)}t^{2/\alpha}dh\\ &=\int_{0}^{\infty}\frac{1}{t^{(n+m)/2}h^{1+\alpha/2+(n+m)/2}}e^{-c_m|x|^2/(t^{2/\alpha}h)}dh. \end{align*} $$
$$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right|&=\left| \int_{0}^{\infty}\eta_t^{\alpha}(s)\frac{\partial^mK_s(x)}{\partial x_j^m}ds\right| \\ &\lesssim\int_{0}^{\infty}\left| \frac{t}{s^{1+\alpha}}\frac{\partial^mK_s(x)}{\partial x_j^m}\right| ds\\ &\lesssim\int_{0}^{\infty}\frac{t}{s^{1+\alpha}} s^{-(n+m)/2}e^{-c_m|x|^2/s}\bigg|_{s=t^{2/\alpha}h}ds\\ &\lesssim\int_{0}^{\infty}\frac{t}{(t^{2/\alpha}h)^{1+\alpha/2+(n+m)/2}}e^{-c_m|x|^2/(t^{2/\alpha}h)}t^{2/\alpha}dh\\ &=\int_{0}^{\infty}\frac{1}{t^{(n+m)/2}h^{1+\alpha/2+(n+m)/2}}e^{-c_m|x|^2/(t^{2/\alpha}h)}dh. \end{align*} $$
Let
![]() $y=t^{2/\alpha }h/|x|^2$
. It holds
$y=t^{2/\alpha }h/|x|^2$
. It holds
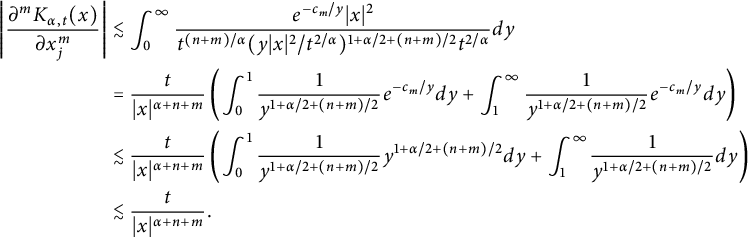 $$ \begin{align*} \left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| &\lesssim\int_{0}^{\infty}\frac{e^{-c_m/y}|x|^2}{t^{(n+m)/\alpha}(y|x|^2/t^{2/\alpha})^{1+\alpha/2+(n+m)/2}t^{2/\alpha}}dy\\ &=\frac{t}{|x|^{\alpha+n+m}}\left( \int_{0}^{1}\frac{1}{y^{1+\alpha/2+(n+m)/2}}e^{-c_m/y}dy+\int_{1}^{\infty}\frac{1}{y^{1+\alpha/2+(n+m)/2}}e^{-c_m/y}dy\right)\\ &\lesssim\frac{t}{|x|^{\alpha+n+m}}\left( \int_{0}^{1}\frac{1}{y^{1+\alpha/2+(n+m)/2}}y^{1+\alpha/2+(n+m)/2}dy+\int_{1}^{\infty}\kern-1pt\frac{1}{y^{1+\alpha/2+(n+m)/2}}dy\right)\\ &\lesssim\frac{t}{|x|^{\alpha+n+m}}. \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| &\lesssim\int_{0}^{\infty}\frac{e^{-c_m/y}|x|^2}{t^{(n+m)/\alpha}(y|x|^2/t^{2/\alpha})^{1+\alpha/2+(n+m)/2}t^{2/\alpha}}dy\\ &=\frac{t}{|x|^{\alpha+n+m}}\left( \int_{0}^{1}\frac{1}{y^{1+\alpha/2+(n+m)/2}}e^{-c_m/y}dy+\int_{1}^{\infty}\frac{1}{y^{1+\alpha/2+(n+m)/2}}e^{-c_m/y}dy\right)\\ &\lesssim\frac{t}{|x|^{\alpha+n+m}}\left( \int_{0}^{1}\frac{1}{y^{1+\alpha/2+(n+m)/2}}y^{1+\alpha/2+(n+m)/2}dy+\int_{1}^{\infty}\kern-1pt\frac{1}{y^{1+\alpha/2+(n+m)/2}}dy\right)\\ &\lesssim\frac{t}{|x|^{\alpha+n+m}}. \end{align*} $$
On the other hand, the fact
![]() $\eta _t^\alpha (s)= (1/t^{2/\alpha })\eta _1^\alpha (s/t^{2/\alpha })$
implies
$\eta _t^\alpha (s)= (1/t^{2/\alpha })\eta _1^\alpha (s/t^{2/\alpha })$
implies
 $$ \begin{align*} \left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| &\lesssim \int_{0}^{\infty}\frac{1}{t^{2/\alpha}}\eta_1^\alpha\left( \frac{s}{t^{2/\alpha}}\right) \frac{1}{s^{(n+m)/2}}ds\\ &\lesssim \frac{1}{t^{(n+m)/\alpha}}\int_{0}^{\infty}\frac{\eta_1^\alpha(h)}{h^{(n+m)/2}}dh. \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| &\lesssim \int_{0}^{\infty}\frac{1}{t^{2/\alpha}}\eta_1^\alpha\left( \frac{s}{t^{2/\alpha}}\right) \frac{1}{s^{(n+m)/2}}ds\\ &\lesssim \frac{1}{t^{(n+m)/\alpha}}\int_{0}^{\infty}\frac{\eta_1^\alpha(h)}{h^{(n+m)/2}}dh. \end{align*} $$
By (2.10), we get
which gives
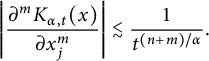 $$ \begin{align*}\left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim \frac{1}{t^{(n+m)/\alpha}}.\end{align*} $$
$$ \begin{align*}\left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim \frac{1}{t^{(n+m)/\alpha}}.\end{align*} $$
Thus, it indicates that
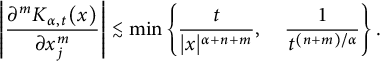 $$ \begin{align*}\left|\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim \min\left\lbrace \frac{t}{|x|^{\alpha+n+m}},\quad\frac{1}{t^{(n+m)/\alpha}}\right\rbrace.\end{align*} $$
$$ \begin{align*}\left|\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim \min\left\lbrace \frac{t}{|x|^{\alpha+n+m}},\quad\frac{1}{t^{(n+m)/\alpha}}\right\rbrace.\end{align*} $$
Case 1:
![]() $0\leq t^{1/\alpha }\leq |x|$
. We have
$0\leq t^{1/\alpha }\leq |x|$
. We have
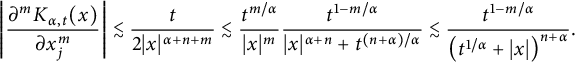 $$ \begin{align*}\left|\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim\frac{t}{2|x|^{\alpha+n+m}}\lesssim \frac{t^{m/\alpha}}{|x|^{m}}\frac{t^{1-m/\alpha}}{|x|^{\alpha+n}+t^{(n+\alpha)/\alpha}}\lesssim \frac{t^{1-m/\alpha}}{\left( t^{1/\alpha}+|x|\right)^{n+\alpha} } .\end{align*} $$
$$ \begin{align*}\left|\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim\frac{t}{2|x|^{\alpha+n+m}}\lesssim \frac{t^{m/\alpha}}{|x|^{m}}\frac{t^{1-m/\alpha}}{|x|^{\alpha+n}+t^{(n+\alpha)/\alpha}}\lesssim \frac{t^{1-m/\alpha}}{\left( t^{1/\alpha}+|x|\right)^{n+\alpha} } .\end{align*} $$
Case 2:
![]() $|x|<t^{1/\alpha }.$
It can be deduced that
$|x|<t^{1/\alpha }.$
It can be deduced that
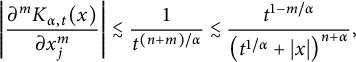 $$ \begin{align*}\left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim \frac{1}{t^{(n+m)/\alpha}}\lesssim \frac{t^{1-m/\alpha}}{\left( t^{1/\alpha}+|x|\right)^{n+\alpha} },\end{align*} $$
$$ \begin{align*}\left| \frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right| \lesssim \frac{1}{t^{(n+m)/\alpha}}\lesssim \frac{t^{1-m/\alpha}}{\left( t^{1/\alpha}+|x|\right)^{n+\alpha} },\end{align*} $$
which gives
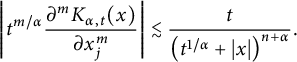 $$ \begin{align*}\left| t^{m/\alpha}\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right|\lesssim \frac{t}{\left( t^{1/\alpha}+|x|\right)^{n+\alpha} } .\\[-45pt]\end{align*} $$
$$ \begin{align*}\left| t^{m/\alpha}\frac{\partial^mK_{\alpha,t}(x)}{\partial x_j^m}\right|\lesssim \frac{t}{\left( t^{1/\alpha}+|x|\right)^{n+\alpha} } .\\[-45pt]\end{align*} $$
Lemma 2.9 For
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha> 1/2$
,
$\alpha> 1/2$
,
![]() $\beta \in (0,1]$
and
$\beta \in (0,1]$
and
![]() $t>0$
, there holds
$t>0$
, there holds
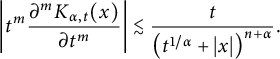 $$ \begin{align*}\left| t^m\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m}\right| \lesssim \frac{t}{\left(t^{1/\alpha}+|x| \right)^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left| t^m\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m}\right| \lesssim \frac{t}{\left(t^{1/\alpha}+|x| \right)^{n+\alpha}}.\end{align*} $$
Proof By (2.10), we get
Then
By (2.2) and the higher-order derivative formula of composite functions, we can obtain
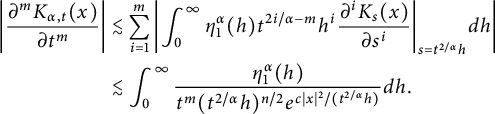 $$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right| &\lesssim \sum_{i=1}^{m}\left|\int_{0}^{\infty} \eta_1^\alpha(h)t^{2i/\alpha-m}h^i\frac{\partial^iK_s(x)}{\partial s^i}\bigg|_{s=t^{2/\alpha}h} dh \right|\\ &\lesssim \int_{0}^{\infty}\frac{\eta_1^\alpha(h)}{t^m(t^{2/\alpha }h)^{n/2}e^{c|x|^2/(t^{2/\alpha }h)}}dh. \end{align*} $$
$$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right| &\lesssim \sum_{i=1}^{m}\left|\int_{0}^{\infty} \eta_1^\alpha(h)t^{2i/\alpha-m}h^i\frac{\partial^iK_s(x)}{\partial s^i}\bigg|_{s=t^{2/\alpha}h} dh \right|\\ &\lesssim \int_{0}^{\infty}\frac{\eta_1^\alpha(h)}{t^m(t^{2/\alpha }h)^{n/2}e^{c|x|^2/(t^{2/\alpha }h)}}dh. \end{align*} $$
Letting
![]() $s=t^{2/\alpha }h/|x|^2$
and
$s=t^{2/\alpha }h/|x|^2$
and
![]() $y=t^{2/\alpha }h/|x|^2,$
we can get
$y=t^{2/\alpha }h/|x|^2,$
we can get
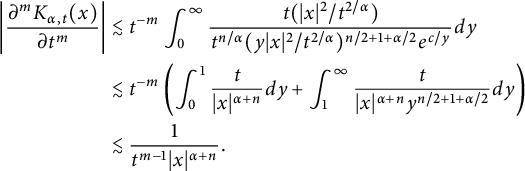 $$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right|&\lesssim t^{-m}\int_{0}^{\infty}\frac{t(|x|^2/t^{2/\alpha})}{t^{n/\alpha}(y|x|^2/t^{2/\alpha})^{n/2+1+\alpha/2}e^{c/y}}dy\\ &\lesssim t^{-m}\left( \int_{0}^{1}\frac{t}{|x|^{\alpha+n}}dy+\int_{1}^{\infty}\frac{t}{|x|^{\alpha+n}y^{n/2+1+\alpha/2}}dy\right)\\ &\lesssim \frac{1}{t^{m-1}|x|^{\alpha+n}}. \end{align*} $$
$$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right|&\lesssim t^{-m}\int_{0}^{\infty}\frac{t(|x|^2/t^{2/\alpha})}{t^{n/\alpha}(y|x|^2/t^{2/\alpha})^{n/2+1+\alpha/2}e^{c/y}}dy\\ &\lesssim t^{-m}\left( \int_{0}^{1}\frac{t}{|x|^{\alpha+n}}dy+\int_{1}^{\infty}\frac{t}{|x|^{\alpha+n}y^{n/2+1+\alpha/2}}dy\right)\\ &\lesssim \frac{1}{t^{m-1}|x|^{\alpha+n}}. \end{align*} $$
On the other hand, the fact
![]() $\int _{0}^{\infty }\eta _1^\alpha (h)h^{-n/2}dh<\infty $
implies
$\int _{0}^{\infty }\eta _1^\alpha (h)h^{-n/2}dh<\infty $
implies
 $$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right|&\lesssim \int_{0}^{\infty}\frac{\eta_1^\alpha(h)}{t^m(t^{2/\alpha }h)^{n/2}e^{c|x|^2/(t^{2/\alpha }h)}}dh\\ &\lesssim t^{-(m+n/\alpha)}\int_{0}^{\infty}\eta_1^\alpha(h)/h^{n/2}dh\\ &\lesssim t^{-(m+n/\alpha)}. \end{align*} $$
$$ \begin{align*} \left|\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right|&\lesssim \int_{0}^{\infty}\frac{\eta_1^\alpha(h)}{t^m(t^{2/\alpha }h)^{n/2}e^{c|x|^2/(t^{2/\alpha }h)}}dh\\ &\lesssim t^{-(m+n/\alpha)}\int_{0}^{\infty}\eta_1^\alpha(h)/h^{n/2}dh\\ &\lesssim t^{-(m+n/\alpha)}. \end{align*} $$
Thus, we can get
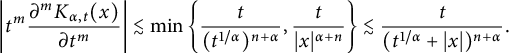 $$ \begin{align*}\left|t^m\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right|\lesssim\min\left\lbrace \frac{t}{(t^{1/\alpha})^{n+\alpha}},\frac{t}{|x|^{\alpha+n}}\right\rbrace \lesssim \frac{t}{(t^{1/\alpha}+|x|)^{n+\alpha}}.\\[-42pt]\end{align*} $$
$$ \begin{align*}\left|t^m\frac{\partial^mK_{\alpha,t}(x)}{\partial t^m} \right|\lesssim\min\left\lbrace \frac{t}{(t^{1/\alpha})^{n+\alpha}},\frac{t}{|x|^{\alpha+n}}\right\rbrace \lesssim \frac{t}{(t^{1/\alpha}+|x|)^{n+\alpha}}.\\[-42pt]\end{align*} $$
Below, we estimate the regularity of the time-space fractional heat kernel
![]() $G^{\alpha ,\beta }_{t}(\cdot )$
.
$G^{\alpha ,\beta }_{t}(\cdot )$
.
Proposition 2.10 Let
![]() $\alpha> n+m$
,
$\alpha> n+m$
,
![]() $m\in \mathbb {Z}_+$
and
$m\in \mathbb {Z}_+$
and
![]() $\beta \in (0,1]$
. Then
$\beta \in (0,1]$
. Then
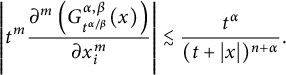 $$ \begin{align*}\left|t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x)\right)}{\partial x_i^m}\right| \lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left|t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x)\right)}{\partial x_i^m}\right| \lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}}.\end{align*} $$
Proof By Lemma 2.8, we know
 $$ \begin{align*} \left| \frac{\partial^m\left(G_{t^{\alpha/\beta}}^{\alpha,\beta}(x)\right)}{\partial x_i^m}\right| &=\left| \int_{0}^{\infty}\frac{\partial^mK_{\alpha,({t^{\alpha/\beta}/u})^\beta}(x)}{\partial x_i^m}g_\beta(u)d{u}\right| \notag\\ &\lesssim\int_{0}^{\infty}\frac{(t^{\alpha/\beta}/u)^{\beta(1-m/\alpha)}g_\beta(u)}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}\notag\\ &=I+II,\notag \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^m\left(G_{t^{\alpha/\beta}}^{\alpha,\beta}(x)\right)}{\partial x_i^m}\right| &=\left| \int_{0}^{\infty}\frac{\partial^mK_{\alpha,({t^{\alpha/\beta}/u})^\beta}(x)}{\partial x_i^m}g_\beta(u)d{u}\right| \notag\\ &\lesssim\int_{0}^{\infty}\frac{(t^{\alpha/\beta}/u)^{\beta(1-m/\alpha)}g_\beta(u)}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}\notag\\ &=I+II,\notag \end{align*} $$
where
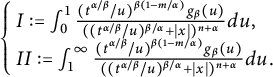 $$ \begin{align*} \begin{cases} & \hspace{-8pt} I:=\int_{0}^{1}\frac{(t^{\alpha/\beta}/u)^{\beta(1-m/\alpha)}g_\beta(u)}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u},\\& \hspace{-8pt}II:=\int_{1}^{\infty}\frac{(t^{\alpha/\beta}/u)^{\beta(1-m/\alpha)}g_\beta(u)}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} & \hspace{-8pt} I:=\int_{0}^{1}\frac{(t^{\alpha/\beta}/u)^{\beta(1-m/\alpha)}g_\beta(u)}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u},\\& \hspace{-8pt}II:=\int_{1}^{\infty}\frac{(t^{\alpha/\beta}/u)^{\beta(1-m/\alpha)}g_\beta(u)}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}. \end{cases} \end{align*} $$
For the term I, by Definition 2.1, since
![]() $\lim \limits _{u\to 0}g_\beta (u)=0$
, we can get
$\lim \limits _{u\to 0}g_\beta (u)=0$
, we can get
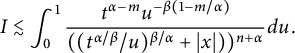 $$ \begin{align*} I\lesssim\int_{0}^{1}\frac{t^{\alpha-m}u^{-\beta(1-m/\alpha)}}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|))^{n+\alpha}}d{u}. \end{align*} $$
$$ \begin{align*} I\lesssim\int_{0}^{1}\frac{t^{\alpha-m}u^{-\beta(1-m/\alpha)}}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|))^{n+\alpha}}d{u}. \end{align*} $$
Since
![]() $\alpha>0$
,
$\alpha>0$
,
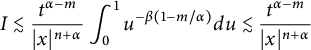 $$ \begin{align*} I\lesssim\frac{t^{\alpha-m}}{|x|^{n+\alpha}}\int_{0}^{1}u^{-\beta(1-m/\alpha)}du\lesssim\frac{t^{\alpha-m}}{|x|^{n+\alpha}} \end{align*} $$
$$ \begin{align*} I\lesssim\frac{t^{\alpha-m}}{|x|^{n+\alpha}}\int_{0}^{1}u^{-\beta(1-m/\alpha)}du\lesssim\frac{t^{\alpha-m}}{|x|^{n+\alpha}} \end{align*} $$
and
When
![]() $u\to \infty $
and
$u\to \infty $
and
![]() $m<\alpha $
, we know
$m<\alpha $
, we know
![]() $g_\beta (u)\approx \frac {\beta }{\Gamma (1-\beta )}u^{-\beta -1}$
. Then
$g_\beta (u)\approx \frac {\beta }{\Gamma (1-\beta )}u^{-\beta -1}$
. Then
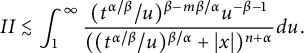 $$ \begin{align*} II&\lesssim\int_{1}^{\infty}\frac{(t^{\alpha/\beta}/u)^{\beta-m\beta/\alpha}u^{-\beta-1}}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}. \end{align*} $$
$$ \begin{align*} II&\lesssim\int_{1}^{\infty}\frac{(t^{\alpha/\beta}/u)^{\beta-m\beta/\alpha}u^{-\beta-1}}{(({t^{\alpha/\beta}/u})^{{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}. \end{align*} $$
We can obtain
and
Let
![]() $\alpha>n+m$
. If
$\alpha>n+m$
. If
![]() $|x|<t$
,
$|x|<t$
,
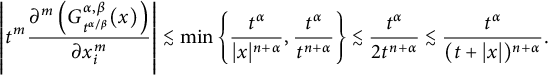 $$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x)\right)}{\partial x_i^m} \right|\lesssim \min\left\lbrace \frac{t^\alpha}{|x|^{n+\alpha}}, \frac{t^\alpha}{t^{n+\alpha}} \right\rbrace \lesssim\frac{t^\alpha}{2t^{n+\alpha}}\lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x)\right)}{\partial x_i^m} \right|\lesssim \min\left\lbrace \frac{t^\alpha}{|x|^{n+\alpha}}, \frac{t^\alpha}{t^{n+\alpha}} \right\rbrace \lesssim\frac{t^\alpha}{2t^{n+\alpha}}\lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}}.\end{align*} $$
On the other hand, if
![]() $|x|\geq t$
,
$|x|\geq t$
,
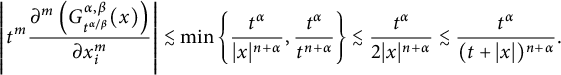 $$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x)\right)}{\partial x_i^m} \right|\lesssim \min\left\lbrace \frac{t^\alpha}{|x|^{n+\alpha}}, \frac{t^\alpha}{t^{n+\alpha}} \right\rbrace \lesssim\frac{t^\alpha}{2|x|^{n+\alpha}}\lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x)\right)}{\partial x_i^m} \right|\lesssim \min\left\lbrace \frac{t^\alpha}{|x|^{n+\alpha}}, \frac{t^\alpha}{t^{n+\alpha}} \right\rbrace \lesssim\frac{t^\alpha}{2|x|^{n+\alpha}}\lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}}.\end{align*} $$
Then
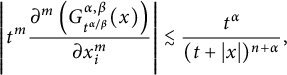 $$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial x_i^m}\right| \lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}},\end{align*} $$
$$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial x_i^m}\right| \lesssim \frac{t^\alpha}{(t+|x|)^{n+\alpha}},\end{align*} $$
which proves Proposition 2.10.
Similarly, we can obtain the following result.
Proposition 2.11 For
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
and
$\beta \in (0,1] $
and
![]() $t>0$
, there holds
$t>0$
, there holds
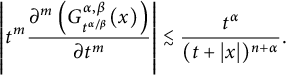 $$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| \lesssim \frac{t^{\alpha}}{(t+|x|)^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left| t^m\frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| \lesssim \frac{t^{\alpha}}{(t+|x|)^{n+\alpha}}.\end{align*} $$
Proof At first, (2.1) implies
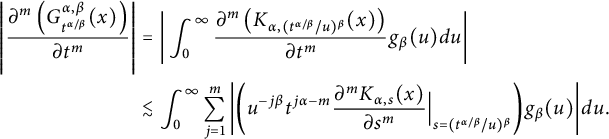 $$ \begin{align*} \left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| &= \bigg|\int_{0}^{\infty} \frac{\partial^m\left( K_{\alpha,({t^{\alpha/\beta}/u})^\beta}(x)\right)}{\partial t^m} g_\beta(u)d{u}\bigg|\notag\\ &\lesssim \int_{0}^{\infty}\sum_{j=1}^{m}\bigg| \bigg( u^{-j\beta}t^{j\alpha-m} \frac{\partial^mK_{\alpha,s}(x)}{\partial s^m}\Big|_{s=({t^{\alpha/\beta}/u})^\beta} \bigg) g_\beta(u)\bigg|d{u}.\notag \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| &= \bigg|\int_{0}^{\infty} \frac{\partial^m\left( K_{\alpha,({t^{\alpha/\beta}/u})^\beta}(x)\right)}{\partial t^m} g_\beta(u)d{u}\bigg|\notag\\ &\lesssim \int_{0}^{\infty}\sum_{j=1}^{m}\bigg| \bigg( u^{-j\beta}t^{j\alpha-m} \frac{\partial^mK_{\alpha,s}(x)}{\partial s^m}\Big|_{s=({t^{\alpha/\beta}/u})^\beta} \bigg) g_\beta(u)\bigg|d{u}.\notag \end{align*} $$
Then it follows from Proposition 2.10 that
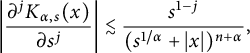 $$ \begin{align*}\left| \frac{\partial^jK_{\alpha,s}(x)}{\partial s^j}\right| \lesssim \frac{s^{1-j}}{(s^{1/\alpha}+|x|)^{n+\alpha}},\end{align*} $$
$$ \begin{align*}\left| \frac{\partial^jK_{\alpha,s}(x)}{\partial s^j}\right| \lesssim \frac{s^{1-j}}{(s^{1/\alpha}+|x|)^{n+\alpha}},\end{align*} $$
which yields
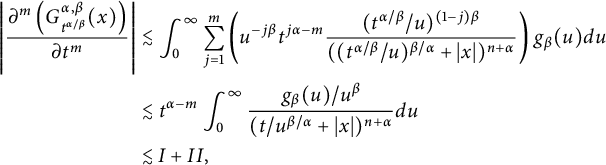 $$ \begin{align*} \left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| &\lesssim \int_{0}^{\infty}\sum_{j=1}^{m} \left( u^{-j\beta}t^{j\alpha-m} \frac{(t^{\alpha/\beta}/u)^{(1-j)\beta}}{((t^{\alpha/\beta}/u)^{\beta/\alpha}+|x|)^{n+\alpha}} \right) g_\beta(u)d{u}\\ &\lesssim t^{\alpha-m}\int_{0}^{\infty}\frac{g_\beta(u)/u^\beta}{({t/u^{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}\\ &\lesssim I+II, \notag \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| &\lesssim \int_{0}^{\infty}\sum_{j=1}^{m} \left( u^{-j\beta}t^{j\alpha-m} \frac{(t^{\alpha/\beta}/u)^{(1-j)\beta}}{((t^{\alpha/\beta}/u)^{\beta/\alpha}+|x|)^{n+\alpha}} \right) g_\beta(u)d{u}\\ &\lesssim t^{\alpha-m}\int_{0}^{\infty}\frac{g_\beta(u)/u^\beta}{({t/u^{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}\\ &\lesssim I+II, \notag \end{align*} $$
where
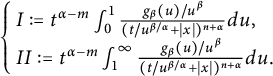 $$ \begin{align*} \begin{cases} & \hspace{-8pt}I:=t^{\alpha-m}\int_{0}^{1}\frac{g_\beta(u)/u^\beta}{({t/u^{\beta/\alpha}}+|x|)^{n+\alpha}}d{u},\\ &\hspace{-8pt}II:=t^{\alpha-m}\int_{1}^{\infty}\frac{g_\beta(u)/u^\beta}{({t/u^{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} & \hspace{-8pt}I:=t^{\alpha-m}\int_{0}^{1}\frac{g_\beta(u)/u^\beta}{({t/u^{\beta/\alpha}}+|x|)^{n+\alpha}}d{u},\\ &\hspace{-8pt}II:=t^{\alpha-m}\int_{1}^{\infty}\frac{g_\beta(u)/u^\beta}{({t/u^{\beta/\alpha}}+|x|)^{n+\alpha}}d{u}. \end{cases} \end{align*} $$
According to [Reference Foondun and Nane17, (2.4) and (2.5)], we have
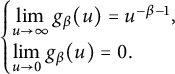 $$ \begin{align*} \begin{cases} \lim\limits_{u\to \infty}g_\beta(u)=u^{-\beta-1},\\ \lim\limits_{u\to 0}g_\beta(u)=0. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \lim\limits_{u\to \infty}g_\beta(u)=u^{-\beta-1},\\ \lim\limits_{u\to 0}g_\beta(u)=0. \end{cases} \end{align*} $$
Noting that
![]() $\alpha>n$
and
$\alpha>n$
and
![]() ${\beta (n+\alpha )/\alpha }<2\beta $
, we can obtain
${\beta (n+\alpha )/\alpha }<2\beta $
, we can obtain
and
On the other hand, since
 $$ \begin{align*} \left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| \lesssim \frac{t^{\alpha-m}}{|x|^{n+\alpha}}\int_{1}^{\infty}u^{-2\beta-1}d{u}+\frac{t^{\alpha-m}}{|x|^{n+\alpha}}\int_{0}^{1}u^{-\beta}d{u} \lesssim \frac{t^{\alpha-m}}{|x|^{n+\alpha}}, \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| \lesssim \frac{t^{\alpha-m}}{|x|^{n+\alpha}}\int_{1}^{\infty}u^{-2\beta-1}d{u}+\frac{t^{\alpha-m}}{|x|^{n+\alpha}}\int_{0}^{1}u^{-\beta}d{u} \lesssim \frac{t^{\alpha-m}}{|x|^{n+\alpha}}, \end{align*} $$
we get
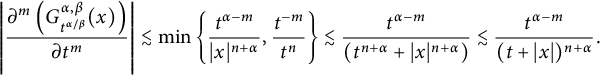 $$ \begin{align*}\left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| \lesssim\min{\left\lbrace \frac{t^{\alpha-m}}{|x|^{n+\alpha}},\frac{t^{-m}}{t^{n}}\right\rbrace }\lesssim \frac{t^{\alpha-m}}{(t^{n+\alpha}+|x|^{n+\alpha})}\lesssim \frac{t^{\alpha-m}}{(t+|x|)^{n+\alpha}}.\end{align*} $$
$$ \begin{align*}\left| \frac{\partial^m\left(G^{\alpha,\beta}_{t^{{\alpha/\beta}}}(x)\right)}{\partial t^m}\right| \lesssim\min{\left\lbrace \frac{t^{\alpha-m}}{|x|^{n+\alpha}},\frac{t^{-m}}{t^{n}}\right\rbrace }\lesssim \frac{t^{\alpha-m}}{(t^{n+\alpha}+|x|^{n+\alpha})}\lesssim \frac{t^{\alpha-m}}{(t+|x|)^{n+\alpha}}.\end{align*} $$
The proof of Proposition 2.11 is completed.
3 Fractional trace inequalities via the time-space fractional extension
3.1 Fractional trace inequalities involving
 $\widetilde {\nabla }^m_{x}u(x,t^{{\alpha /\beta }})$
and
$\widetilde {\nabla }^m_{x}u(x,t^{{\alpha /\beta }})$
and
 $\frac {\partial ^mu(x,t^{\alpha /\beta })}{\partial t^m}$
$\frac {\partial ^mu(x,t^{\alpha /\beta })}{\partial t^m}$
Theorem 3.1 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
. For
$\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x)$
the time-space fractional extension of f.
$u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x)$
the time-space fractional extension of f.
-
(i) There holds
(3.1) $$ \begin{align} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
-
(ii) If
 $\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds (3.2)
$\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds (3.2) $$ \begin{align} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
$$ \begin{align} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
-
(iii) There holds
(3.3) $$ \begin{align} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^\nu}\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^\nu}\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
Proof In order to prove (i) of Theorem 3.1, we need to establish the following result: for
![]() $\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
,
$\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
,
In fact, notice that
![]() $u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
. It holds
$u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
. It holds
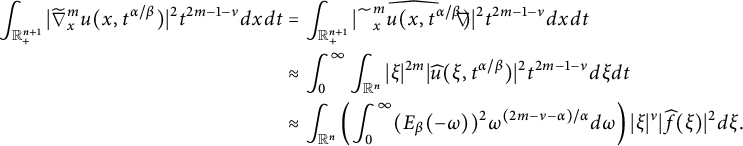 $$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t} &= \int_{\mathbb{R}_{+}^{n+1}}|\widehat{\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})}|^2t^{2m-1-\nu}d{x}d{t} \notag\\ &\approx \int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2m}|\widehat{u}(\xi,t^{{\alpha/\beta}})|^2 t^{2m-1-\nu}d{\xi}d{t} \notag\\ &\approx \int_{\mathbb{R}^n}\left( \int_{0}^{\infty}(E_\beta(-\omega))^2\omega^{(2m-\nu-\alpha)/\alpha}d{\omega}\right) |\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}.\notag \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t} &= \int_{\mathbb{R}_{+}^{n+1}}|\widehat{\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})}|^2t^{2m-1-\nu}d{x}d{t} \notag\\ &\approx \int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2m}|\widehat{u}(\xi,t^{{\alpha/\beta}})|^2 t^{2m-1-\nu}d{\xi}d{t} \notag\\ &\approx \int_{\mathbb{R}^n}\left( \int_{0}^{\infty}(E_\beta(-\omega))^2\omega^{(2m-\nu-\alpha)/\alpha}d{\omega}\right) |\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}.\notag \end{align*} $$
In (2.4) of Lemma 2.5, take
![]() $\nu \in (0,\min \{2m,n\})$
and
$\nu \in (0,\min \{2m,n\})$
and
![]() $m<\alpha $
. We get
$m<\alpha $
. We get
Hence
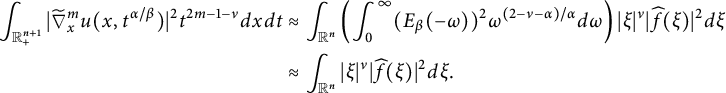 $$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}&\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}(E_\beta(-\omega))^2\omega^{{(2-\nu-\alpha)/\alpha}}d{\omega}\right) |\xi|^\nu| \widehat{f}(\xi)| ^2d{\xi}\\ &\approx \int_{\mathbb{R}^n}|\xi|^\nu| \widehat{f}(\xi)| ^2d{\xi}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{{\alpha/\beta}})|^2t^{2m-1-\nu}d{x}d{t}&\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}(E_\beta(-\omega))^2\omega^{{(2-\nu-\alpha)/\alpha}}d{\omega}\right) |\xi|^\nu| \widehat{f}(\xi)| ^2d{\xi}\\ &\approx \int_{\mathbb{R}^n}|\xi|^\nu| \widehat{f}(\xi)| ^2d{\xi}. \end{align*} $$
We know that
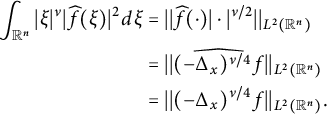 $$ \begin{align*} \int_{\mathbb{R}^n}|\xi|^\nu|\widehat{f}(\xi)|^2d{\xi} &=\vert\vert \widehat{f}(\cdot)|\cdot|^{{\nu/2}}\vert\vert_{L^2(\mathbb{R}^n)}\notag\\ &=\vert\vert \widehat{(-\Delta_x)^{{\nu/4}}f}\vert\vert_{L^2(\mathbb{R}^n)}\notag\\ &=\vert\vert{(-\Delta_x)^{{\nu/4}}f}\vert\vert_{L^2(\mathbb{R}^n)}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}|\xi|^\nu|\widehat{f}(\xi)|^2d{\xi} &=\vert\vert \widehat{f}(\cdot)|\cdot|^{{\nu/2}}\vert\vert_{L^2(\mathbb{R}^n)}\notag\\ &=\vert\vert \widehat{(-\Delta_x)^{{\nu/4}}f}\vert\vert_{L^2(\mathbb{R}^n)}\notag\\ &=\vert\vert{(-\Delta_x)^{{\nu/4}}f}\vert\vert_{L^2(\mathbb{R}^n)}. \end{align*} $$
It follows from the well-known fractional Sobolev inequality:
for
![]() $\nu \in (0,n)$
and some constant
$\nu \in (0,n)$
and some constant
![]() $B(n,\nu )$
that (3.1) holds.
$B(n,\nu )$
that (3.1) holds.
Now, we want to prove (ii) of Theorem 3.1. Let
![]() $p=n(r-2)/\nu $
,
$p=n(r-2)/\nu $
,
![]() $2<r<2n/(n-\nu )$
and
$2<r<2n/(n-\nu )$
and
![]() $\nu \in (0,\min \{n,2m\})$
. The Hölder inequality implies that
$\nu \in (0,\min \{n,2m\})$
. The Hölder inequality implies that
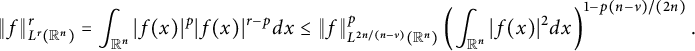 $$ \begin{align} \|f\|^{r}_{L^{r}(\mathbb{R}^n)}=\int_{\mathbb{R}^n}|f(x)|^p|f(x)|^{r-p}d{x}\leq\|f\|^{p}_{L^{2n/(n-\nu)}(\mathbb{R}^n)}\left( \int_{\mathbb{R}^n}|f(x)|^2d{x} \right)^{{1-p(n-\nu)/(2n)}}. \end{align} $$
$$ \begin{align} \|f\|^{r}_{L^{r}(\mathbb{R}^n)}=\int_{\mathbb{R}^n}|f(x)|^p|f(x)|^{r-p}d{x}\leq\|f\|^{p}_{L^{2n/(n-\nu)}(\mathbb{R}^n)}\left( \int_{\mathbb{R}^n}|f(x)|^2d{x} \right)^{{1-p(n-\nu)/(2n)}}. \end{align} $$
If
![]() $\|f\|_{L^2(\mathbb {R}^n)}=1$
, it can be deduced from (3.5) that
$\|f\|_{L^2(\mathbb {R}^n)}=1$
, it can be deduced from (3.5) that
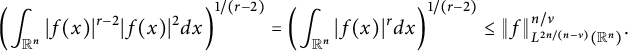 $$ \begin{align*}\left( \int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x} \right)^{1/(r-2)}=\left( \int_{\mathbb{R}^n}|f(x)|^rd{x} \right)^{1/(r-2)}\leq\|f\|^{n/\nu}_{L^{2n/(n-\nu)}(\mathbb{R}^n)}.\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x} \right)^{1/(r-2)}=\left( \int_{\mathbb{R}^n}|f(x)|^rd{x} \right)^{1/(r-2)}\leq\|f\|^{n/\nu}_{L^{2n/(n-\nu)}(\mathbb{R}^n)}.\end{align*} $$
The inequality (3.1) implies that for a positive constant
![]() $A(n,s,\nu )$
,
$A(n,s,\nu )$
,
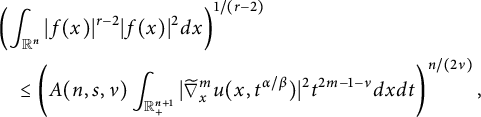 $$ \begin{align*}&\left( \int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x} \right) ^{1/(r-2)}\\&\quad\leq\left( A(n,s,\nu)\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{\alpha/\beta})|^2t^{2m-1-\nu}d{x}d{t} \right)^{n/(2\nu)},\end{align*} $$
$$ \begin{align*}&\left( \int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x} \right) ^{1/(r-2)}\\&\quad\leq\left( A(n,s,\nu)\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{\alpha/\beta})|^2t^{2m-1-\nu}d{x}d{t} \right)^{n/(2\nu)},\end{align*} $$
which yields
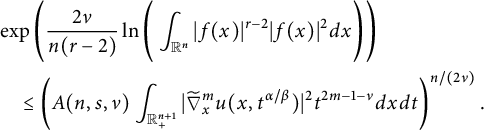 $$ \begin{align*}&\exp\Bigg(\frac{2\nu}{n(r-2)}\ln\Bigg(\int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x}\Bigg)\Bigg)\\&\quad\leq\left( A(n,s,\nu)\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{\alpha/\beta})|^2t^{2m-1-\nu}d{x}d{t} \right)^{n/(2\nu)}.\end{align*} $$
$$ \begin{align*}&\exp\Bigg(\frac{2\nu}{n(r-2)}\ln\Bigg(\int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x}\Bigg)\Bigg)\\&\quad\leq\left( A(n,s,\nu)\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t^{\alpha/\beta})|^2t^{2m-1-\nu}d{x}d{t} \right)^{n/(2\nu)}.\end{align*} $$
Since
![]() $\|f\|_{L^{2}(\mathbb {R}^n)}=1$
,
$\|f\|_{L^{2}(\mathbb {R}^n)}=1$
,
![]() $d\mu (x):=|f(x)|^2dx$
can be treated as a probability measure on
$d\mu (x):=|f(x)|^2dx$
can be treated as a probability measure on
![]() $\mathbb {R}^n$
. Thus (3.2) can be obtained by letting
$\mathbb {R}^n$
. Thus (3.2) can be obtained by letting
![]() $r\rightarrow 2$
. In fact,
$r\rightarrow 2$
. In fact,
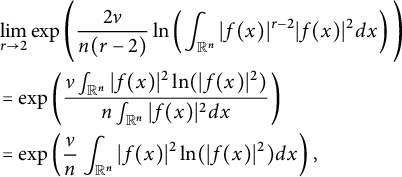 $$ \begin{align*} &\lim\limits_{r\to2}\exp\Bigg(\frac{2\nu}{n(r-2)}\ln\left( \int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x}\right) \Bigg)\notag\\ &= \exp\left(\frac{\nu\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)}{n\int_{\mathbb{R}^n}|f(x)|^2d{x}}\right)\notag\\ &=\exp\left(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\right), \end{align*} $$
$$ \begin{align*} &\lim\limits_{r\to2}\exp\Bigg(\frac{2\nu}{n(r-2)}\ln\left( \int_{\mathbb{R}^n}|f(x)|^{r-2}|f(x)|^2d{x}\right) \Bigg)\notag\\ &= \exp\left(\frac{\nu\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)}{n\int_{\mathbb{R}^n}|f(x)|^2d{x}}\right)\notag\\ &=\exp\left(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\right), \end{align*} $$
which implies (3.2).
At last, the inequality (3.3) follows from (3.4) and the fractional Hardy inequality.
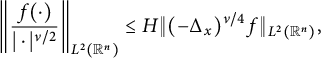 $$ \begin{align*}\left\|\frac{f(\cdot)}{|\cdot|^{\nu/2}}\right\|_{L^2(\mathbb{R}^n)}\leq H\|(-\Delta_x)^{\nu/4}f\|_{L^2(\mathbb{R}^n)},\end{align*} $$
$$ \begin{align*}\left\|\frac{f(\cdot)}{|\cdot|^{\nu/2}}\right\|_{L^2(\mathbb{R}^n)}\leq H\|(-\Delta_x)^{\nu/4}f\|_{L^2(\mathbb{R}^n)},\end{align*} $$
which is a special case of [Reference Xiao and Zhai42, (3.1) in Theorem 3.1]
As an immediate corollary of Theorem 3.1, we can obtain the following result.
Theorem 3.2 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
and
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
and
![]() $\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
. For
$\nu \in (0,\min \left \lbrace 2m,n\right \rbrace )$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x)$
the time-space fractional extension of f. Then, the following statements are true.
$u(x,t)=G_{t}^{\alpha ,\beta }\ast f(x)$
the time-space fractional extension of f. Then, the following statements are true.
-
(i) There holds
 $$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
-
(ii) If
 $\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds
$\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds  $$ \begin{align*} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
-
(iii) There holds
 $$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^\nu}\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^\nu}\lesssim\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
Proof By the change of variable:
![]() $t=\omega ^{\alpha /\beta }$
, we have
$t=\omega ^{\alpha /\beta }$
, we have
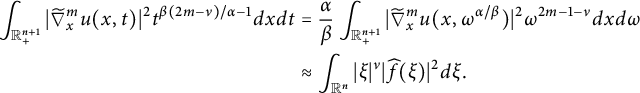 $$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}&=\frac{\alpha}{\beta}\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,\omega^{{\alpha/\beta}})|^2\omega^{2m-1-\nu}d{x}d{\omega}\\ &\approx \int_{\mathbb{R}^n}|\xi|^\nu| \widehat{f}(\xi)| ^2d{\xi}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,t)|^2t^{\beta(2m-\nu)/\alpha-1}d{x}d{t}&=\frac{\alpha}{\beta}\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}^m_{x}u(x,\omega^{{\alpha/\beta}})|^2\omega^{2m-1-\nu}d{x}d{\omega}\\ &\approx \int_{\mathbb{R}^n}|\xi|^\nu| \widehat{f}(\xi)| ^2d{\xi}. \end{align*} $$
Similarly to the proof of Theorem 3.1, we can prove Theorem 3.2.
Theorem 3.3 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \{ 2\alpha , n\})$
. For
$\nu \in (0,\min \{ 2\alpha , n\})$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f.
$u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f.
-
(i) There holds
(3.6) $$ \begin{align} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta})}{\partial t^m}\right| }^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta})}{\partial t^m}\right| }^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
-
(ii) If
 $\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds (3.7)
$\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds (3.7) $$ \begin{align} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta})}{\partial t^m}\right|}^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
$$ \begin{align} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta})}{\partial t^m}\right|}^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
-
(iii) There holds
(3.8) $$ \begin{align} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta})}{\partial t^m}\right| }^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta})}{\partial t^m}\right| }^2t^{2m-1-\nu}d{x}d{t}. \end{align} $$
Proof In order to prove (3.6), we need to prove that for
![]() $\nu \in (0,\min \left \lbrace 2\alpha ,n\right \rbrace )$
, there exists a constant
$\nu \in (0,\min \left \lbrace 2\alpha ,n\right \rbrace )$
, there exists a constant
![]() $a(n,\alpha ,\beta ,\nu )$
such that
$a(n,\alpha ,\beta ,\nu )$
such that
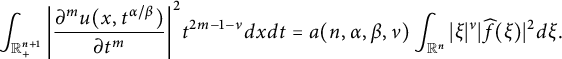 $$ \begin{align*}\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta}) }{\partial t^m}\right| }^2t^{2m-1-\nu}d{x}d{t}=a(n,\alpha,\beta,\nu)\int_{\mathbb{R}^n}^{}|\xi|^{\nu}| \widehat{f}(\xi)| ^2d{\xi}.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t^{\alpha/\beta}) }{\partial t^m}\right| }^2t^{2m-1-\nu}d{x}d{t}=a(n,\alpha,\beta,\nu)\int_{\mathbb{R}^n}^{}|\xi|^{\nu}| \widehat{f}(\xi)| ^2d{\xi}.\end{align*} $$
In fact, noting that
![]() $u(x,t^{\alpha /\beta })=G_{t^{\alpha /\beta }}^{\alpha ,\beta }\ast f(x)$
, we can apply (2.5) to deduce that
$u(x,t^{\alpha /\beta })=G_{t^{\alpha /\beta }}^{\alpha ,\beta }\ast f(x)$
, we can apply (2.5) to deduce that
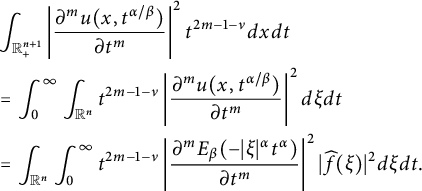 $$ \begin{align*} &\int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m}\right| ^2t^{2m-1-\nu}dxdt\\ &=\int_{0}^{\infty}\int_{\mathbb{R}^{n}}t^{2m-1-\nu} \left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2d\xi dt\\ &=\int_{\mathbb{R}^{n}}\int_{0}^{\infty}t^{2m-1-\nu}\left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m}\right|^2| \widehat{f}(\xi)| ^2d\xi dt. \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m}\right| ^2t^{2m-1-\nu}dxdt\\ &=\int_{0}^{\infty}\int_{\mathbb{R}^{n}}t^{2m-1-\nu} \left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2d\xi dt\\ &=\int_{\mathbb{R}^{n}}\int_{0}^{\infty}t^{2m-1-\nu}\left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m}\right|^2| \widehat{f}(\xi)| ^2d\xi dt. \end{align*} $$
Denote
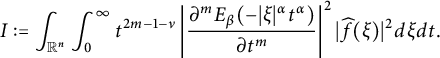 $$ \begin{align*}I:=\int_{\mathbb{R}^{n}}\int_{0}^{\infty}t^{2m-1-\nu}\left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m}\right|^2| \widehat{f}(\xi)| ^2d\xi dt.\end{align*} $$
$$ \begin{align*}I:=\int_{\mathbb{R}^{n}}\int_{0}^{\infty}t^{2m-1-\nu}\left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m}\right|^2| \widehat{f}(\xi)| ^2d\xi dt.\end{align*} $$
Let
![]() $u=|\xi |^\alpha t^\alpha $
. Then
$u=|\xi |^\alpha t^\alpha $
. Then
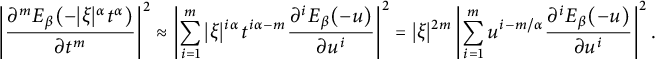 $$ \begin{align*} \left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m}\right|^2 \approx\left|\sum_{i=1}^{m} |\xi|^{i\alpha}t^{i\alpha-m}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 =|\xi|^{2m}\left|\sum_{i=1}^m u^{i-m/\alpha}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right|^2. \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\alpha)}{\partial t^m}\right|^2 \approx\left|\sum_{i=1}^{m} |\xi|^{i\alpha}t^{i\alpha-m}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 =|\xi|^{2m}\left|\sum_{i=1}^m u^{i-m/\alpha}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right|^2. \end{align*} $$
We get
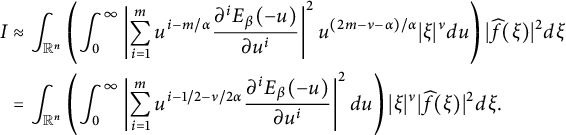 $$ \begin{align*} I&\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}\left|\sum_{i=1}^{m} u^{i-m/\alpha}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 u^{(2m-\nu-\alpha)/\alpha} |\xi|^{\nu}du\right) | \widehat{f}(\xi)| ^2 d\xi\\ &=\int_{\mathbb{R}^n} \left( \int_{0}^{\infty}\left|\sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\right)|\xi|^{\nu}| \widehat{f}(\xi)| ^2d\xi. \end{align*} $$
$$ \begin{align*} I&\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}\left|\sum_{i=1}^{m} u^{i-m/\alpha}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 u^{(2m-\nu-\alpha)/\alpha} |\xi|^{\nu}du\right) | \widehat{f}(\xi)| ^2 d\xi\\ &=\int_{\mathbb{R}^n} \left( \int_{0}^{\infty}\left|\sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\right)|\xi|^{\nu}| \widehat{f}(\xi)| ^2d\xi. \end{align*} $$
By Lemma 2.5, for
![]() $\nu \in (0,\min \{2\alpha ,n\})$
and
$\nu \in (0,\min \{2\alpha ,n\})$
and
![]() $\alpha>m$
, we can obtain
$\alpha>m$
, we can obtain
![]() $-1<2i-1-\nu /\alpha <2i+1$
and
$-1<2i-1-\nu /\alpha <2i+1$
and
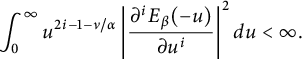 $$ \begin{align*} \int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u) }{\partial u^i}\right|^2 du<\infty. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u) }{\partial u^i}\right|^2 du<\infty. \end{align*} $$
Then
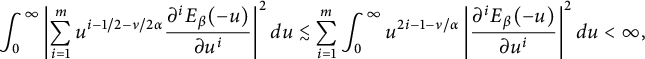 $$ \begin{align*}\int_{0}^{\infty}\left|\sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\lesssim \sum_{i=1}^{m} \int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du<\infty,\end{align*} $$
$$ \begin{align*}\int_{0}^{\infty}\left|\sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\lesssim \sum_{i=1}^{m} \int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du<\infty,\end{align*} $$
which indicates
Theorem 3.3 can be proved in a way similar to that of Theorem 3.1.
Theorem 3.4 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
$f\in \dot {H}^{\nu /2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \{ 2\alpha , n\})$
. For
$\nu \in (0,\min \{ 2\alpha , n\})$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f. Then the following statements are true.
$u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f. Then the following statements are true.
-
(i) There holds
 $$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t)}{\partial t^m}\right| }^2t^{2m-1-\beta\nu/\alpha}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t)}{\partial t^m}\right| }^2t^{2m-1-\beta\nu/\alpha}d{x}d{t}. \end{align*} $$
-
(ii) If
 $\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds
$\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds  $$ \begin{align*} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t)}{\partial t^m}\right|}^2t^{2m-1-\beta\nu/\alpha}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \exp\Bigg(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\Bigg)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t)}{\partial t^m}\right|}^2t^{2m-1-\beta\nu/\alpha}d{x}d{t}. \end{align*} $$
-
(iii) There holds
 $$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t)}{\partial t^m}\right| }^2t^{2m-1-\beta\nu/\alpha}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| \frac{\partial^m u(x,t)}{\partial t^m}\right| }^2t^{2m-1-\beta\nu/\alpha}d{x}d{t}. \end{align*} $$
Proof The proof of this theorem is similar to that of Theorem 3.3. Notice that
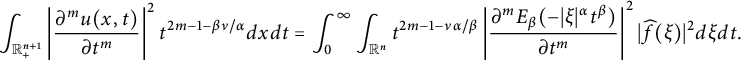 $$ \begin{align*} \int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t)}{\partial t^m}\right|^2 t^{2m-1-\beta\nu/\alpha}dxdt=\int_{0}^{\infty}\int_{\mathbb{R}^{n}}t^{2m-1-\nu\alpha/\beta}\left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\beta)}{\partial t^m}\right|^2| \widehat{f}(\xi)| ^2d\xi dt. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t)}{\partial t^m}\right|^2 t^{2m-1-\beta\nu/\alpha}dxdt=\int_{0}^{\infty}\int_{\mathbb{R}^{n}}t^{2m-1-\nu\alpha/\beta}\left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\beta)}{\partial t^m}\right|^2| \widehat{f}(\xi)| ^2d\xi dt. \end{align*} $$
Letting
![]() $u=|\xi |^\alpha t^\beta $
, we can get
$u=|\xi |^\alpha t^\beta $
, we can get
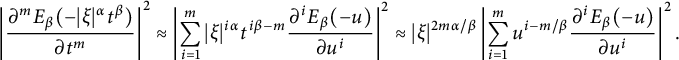 $$ \begin{align*} \left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\beta)}{\partial t^m}\right|^2 \approx \left|\sum_{i=1}^{m} |\xi|^{i\alpha}t^{i\beta-m}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 \approx |\xi|^{2m\alpha/\beta}\left|\sum_{i=1}^m u^{i-m/\beta}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right|^2. \end{align*} $$
$$ \begin{align*} \left| \frac{\partial^mE_\beta(-|\xi|^\alpha t^\beta)}{\partial t^m}\right|^2 \approx \left|\sum_{i=1}^{m} |\xi|^{i\alpha}t^{i\beta-m}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 \approx |\xi|^{2m\alpha/\beta}\left|\sum_{i=1}^m u^{i-m/\beta}\frac{\partial^iE_\beta(-u)}{\partial u^i}\right|^2. \end{align*} $$
Then
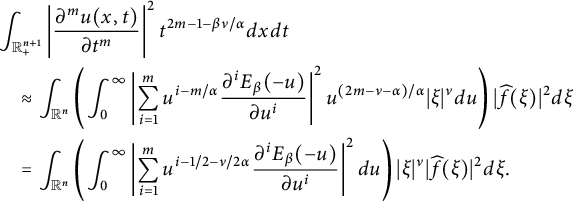 $$ \begin{align*} &\int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t)}{\partial t^m}\right|^2 t^{2m-1-\beta\nu/\alpha}dxdt\\&\quad\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}\left|\sum_{i=1}^{m} u^{i-m/\alpha}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 u^{(2m-\nu-\alpha)/\alpha} |\xi|^{\nu}du\right) | \widehat{f}(\xi)| ^2 d\xi\\ &\quad=\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}\left| \sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\right) |\xi|^{\nu} | \widehat{f}(\xi)| ^2d\xi. \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t)}{\partial t^m}\right|^2 t^{2m-1-\beta\nu/\alpha}dxdt\\&\quad\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}\left|\sum_{i=1}^{m} u^{i-m/\alpha}\frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 u^{(2m-\nu-\alpha)/\alpha} |\xi|^{\nu}du\right) | \widehat{f}(\xi)| ^2 d\xi\\ &\quad=\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}\left| \sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\right) |\xi|^{\nu} | \widehat{f}(\xi)| ^2d\xi. \end{align*} $$
By Lemma 2.5, for
![]() $\nu \in (0,\min \{2\alpha ,n\})$
and
$\nu \in (0,\min \{2\alpha ,n\})$
and
![]() $\alpha>m$
, we can obtain
$\alpha>m$
, we can obtain
![]() $-1<2i-1-\nu /\alpha <2i+1$
and
$-1<2i-1-\nu /\alpha <2i+1$
and
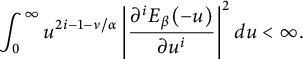 $$ \begin{align*} \int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du<\infty. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du<\infty. \end{align*} $$
Then
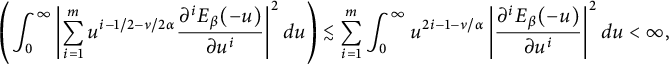 $$ \begin{align*}\left( \int_{0}^{\infty}\left| \sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\right)\lesssim\sum_{i=1}^{m}\int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du<\infty,\end{align*} $$
$$ \begin{align*}\left( \int_{0}^{\infty}\left| \sum_{i=1}^{m}u^{i-1/2-\nu/2\alpha} \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du\right)\lesssim\sum_{i=1}^{m}\int_{0}^{\infty}u^{2i-1-\nu/\alpha}\left| \frac{\partial^iE_\beta(-u)}{\partial u^i} \right|^2 du<\infty,\end{align*} $$
which indicates
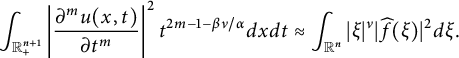 $$ \begin{align*}\int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t)}{\partial t^m}\right|^2 t^{2m-1-\beta\nu/\alpha}dxdt\approx \int_{\mathbb{R}^n}|\xi|^{\nu} | \widehat{f}(\xi)| ^2d\xi.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^{n+1}_+}\left| \frac{\partial^mu(x,t)}{\partial t^m}\right|^2 t^{2m-1-\beta\nu/\alpha}dxdt\approx \int_{\mathbb{R}^n}|\xi|^{\nu} | \widehat{f}(\xi)| ^2d\xi.\end{align*} $$
The rest of the proof is similar to that of Theorem 3.3 and so is omitted.
3.2 Fractional trace inequalities involving
 $(-\Delta _x)^{s/2}u(x,t^{{\alpha /\beta }})$
$(-\Delta _x)^{s/2}u(x,t^{{\alpha /\beta }})$
Theorem 3.5 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n$
,
$\alpha>n$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {H}^{\nu /2}(\mathbb {R}^n)$
with
$f\in \dot {H}^{\nu /2}(\mathbb {R}^n)$
with
![]() $\nu \in (0,n)$
and
$\nu \in (0,n)$
and
![]() $s\in (\nu /2,\alpha +\nu /2)$
. For
$s\in (\nu /2,\alpha +\nu /2)$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G^{\alpha ,\beta }_{t}\ast f(x)$
the extension of f via the time-space fractional heat kernel. Then the following statements are true.
$u(x,t)=G^{\alpha ,\beta }_{t}\ast f(x)$
the extension of f via the time-space fractional heat kernel. Then the following statements are true.
-
(i) There holds
 $$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1}d{x}d{t}. \end{align*} $$
-
(ii) If
 $\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds
$\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds  $$ \begin{align*} \exp\left(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\right)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \exp\left(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\right)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1}d{x}d{t}. \end{align*} $$
-
(iii) There holds
 $$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1}d{x}d{t}. \end{align*} $$
Proof We only need to prove
By (2.4), we have
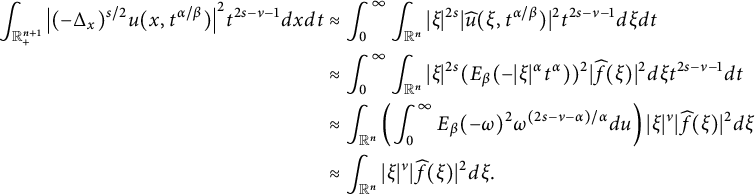 $$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1} d{x}d{t}&\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}|\widehat{u}(\xi,t^{{\alpha/\beta}})|^2t^{2s-\nu-1}d{\xi}d{t}\notag\\ &\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}(E_\beta(-|\xi|^\alpha t^\alpha))^2| \widehat{f}(\xi)| ^2d{\xi} t^{2s-\nu-1}d{t}\notag\\ &\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}E_\beta(-\omega)^2\omega^{{(2s-\nu-\alpha)/\alpha}}d{u} \right) |\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}\notag\\ &\approx\int_{\mathbb{R}^n}|\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t^{{\alpha/\beta}})\right| }^2t^{2s-\nu-1} d{x}d{t}&\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}|\widehat{u}(\xi,t^{{\alpha/\beta}})|^2t^{2s-\nu-1}d{\xi}d{t}\notag\\ &\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}(E_\beta(-|\xi|^\alpha t^\alpha))^2| \widehat{f}(\xi)| ^2d{\xi} t^{2s-\nu-1}d{t}\notag\\ &\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}E_\beta(-\omega)^2\omega^{{(2s-\nu-\alpha)/\alpha}}d{u} \right) |\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}\notag\\ &\approx\int_{\mathbb{R}^n}|\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}. \end{align*} $$
Following the procedure of the proof of Theorem 3.1, we can prove Theorem 3.5 by using (3.9). We omit the details.
Theorem 3.6 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n$
,
$\alpha>n$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {H}^{\nu /2}(\mathbb {R}^n)$
with
$f\in \dot {H}^{\nu /2}(\mathbb {R}^n)$
with
![]() $\nu \in (0,n)$
and
$\nu \in (0,n)$
and
![]() $s\in (\nu /2,\alpha +\nu /2)$
. For
$s\in (\nu /2,\alpha +\nu /2)$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the extension of f via the time-space fractional heat kernel. Then the following statements are true.
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the extension of f via the time-space fractional heat kernel. Then the following statements are true.
-
(i) There holds
 $$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}^n}^{}\left|f(x)\right|^{2n/(n-\nu)}d{x}\right)^{1-\nu/n} \lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
-
(ii) If
 $\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds
$\vert \vert f\vert \vert _{L^2(\mathbb {R}^n)}=1$
, there holds  $$ \begin{align*} \exp\left(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\right)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \exp\left(\frac{\nu}{n}\int_{\mathbb{R}^n}|f(x)|^2\ln(|f(x)|^2)d{x}\right)\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
-
(iii) There holds
 $$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}|f(x)|^2\frac{d{x}}{|x|^{\nu}}\lesssim\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1}d{x}d{t}. \end{align*} $$
Proof Similarly to Theorem 3.5, we only need to prove
It follows from (2.4) that
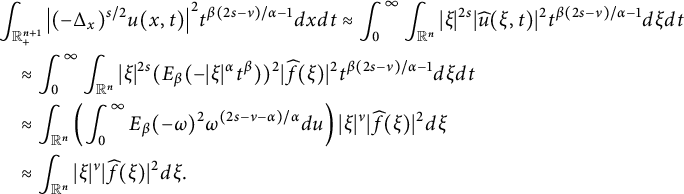 $$ \begin{align*} &\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1} d{x}d{t}\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}|\widehat{u}(\xi,t)|^2t^{\beta(2s-\nu)/\alpha-1}d{\xi}d{t}\notag\\ &\quad\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}(E_\beta(-|\xi|^\alpha t^\beta))^2| \widehat{f}(\xi)| ^2t^{\beta(2s-\nu)/\alpha-1}d{\xi} d{t}\notag\\ &\quad\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}E_\beta(-\omega)^2\omega^{{(2s-\nu-\alpha)/\alpha}}d{u} \right) |\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}\notag\\ &\quad\approx\int_{\mathbb{R}^n}|\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}.\\[-42pt] \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}_{+}^{n+1}}{\left| (-\Delta_x)^{s/2}u(x,t)\right| }^2t^{\beta(2s-\nu)/\alpha-1} d{x}d{t}\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}|\widehat{u}(\xi,t)|^2t^{\beta(2s-\nu)/\alpha-1}d{\xi}d{t}\notag\\ &\quad\approx\int_{0}^{\infty}\int_{\mathbb{R}^n}|\xi|^{2s}(E_\beta(-|\xi|^\alpha t^\beta))^2| \widehat{f}(\xi)| ^2t^{\beta(2s-\nu)/\alpha-1}d{\xi} d{t}\notag\\ &\quad\approx\int_{\mathbb{R}^n}\left( \int_{0}^{\infty}E_\beta(-\omega)^2\omega^{{(2s-\nu-\alpha)/\alpha}}d{u} \right) |\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}\notag\\ &\quad\approx\int_{\mathbb{R}^n}|\xi|^\nu|\widehat{f}(\xi)|^2d{\xi}.\\[-42pt] \end{align*} $$
3.3 The general case
 $p>$
1
$p>$
1
In Theorem 3.1, we consider the scope of
![]() $(p,\nu )$
when
$(p,\nu )$
when
![]() $p=2$
and
$p=2$
and
![]() $\nu \in (0, \min \{n,2\})$
. We can generalize inequalities in Theorem 3.1 to the general case
$\nu \in (0, \min \{n,2\})$
. We can generalize inequalities in Theorem 3.1 to the general case
![]() $p\in (1,\infty ).$
$p\in (1,\infty ).$
To obtain the Sobolev-type trace inequalities for the general index p, we need a characterization of the Sobolev spaces
![]() $\dot {W}^{\nu /2}_{p}(\mathbb R^{n})$
via the time-space fractional heat kernel.
$\dot {W}^{\nu /2}_{p}(\mathbb R^{n})$
via the time-space fractional heat kernel.
Definition 3.7 For
![]() $\tau =(\tau _{1},\tau _{2},\ldots ,\tau _{n}) \in \mathbb {N}^n$
, denote
$\tau =(\tau _{1},\tau _{2},\ldots ,\tau _{n}) \in \mathbb {N}^n$
, denote
![]() $|\tau |=\sum _{i=1}^{n}\tau _i$
and
$|\tau |=\sum _{i=1}^{n}\tau _i$
and
![]() $\partial ^\tau :=\partial ^{\tau _1}_{\xi _1}\dots \partial ^{\tau _n}_{\xi _n}$
.
$\partial ^\tau :=\partial ^{\tau _1}_{\xi _1}\dots \partial ^{\tau _n}_{\xi _n}$
.
-
(C1) (Cancellation) Let
 $\widehat {\Phi }\in C^{n+1+[\Lambda ]}(\mathbb {R}^n\setminus \{0\})$
such that for every
$\widehat {\Phi }\in C^{n+1+[\Lambda ]}(\mathbb {R}^n\setminus \{0\})$
such that for every
 $|\tau |\leq n+1+[\Lambda ]$
, we have
$|\tau |\leq n+1+[\Lambda ]$
, we have  $$ \begin{align*}\partial^{\tau}\widehat{\Phi}=O(|\xi|^{r-|\tau|}) \quad \text{ as } |\xi| \to 0.\end{align*} $$
$$ \begin{align*}\partial^{\tau}\widehat{\Phi}=O(|\xi|^{r-|\tau|}) \quad \text{ as } |\xi| \to 0.\end{align*} $$
-
(C2) For every
 $\xi \in \mathbb {S}^{n-1}$
, there exist
$\xi \in \mathbb {S}^{n-1}$
, there exist
 $a_1,a_2\in \mathbb {R}$
(depending on
$a_1,a_2\in \mathbb {R}$
(depending on
 $\xi $
) with
$\xi $
) with
 $0<2a_1\leq a_2$
such that for every
$0<2a_1\leq a_2$
such that for every
 $a_1<t<a_2$
,
$a_1<t<a_2$
,
 $|\widehat {\Phi }(t\xi )|>0.$
$|\widehat {\Phi }(t\xi )|>0.$
-
(C3) Take
 $\widehat {\Phi }\in C^{n+1+[\Lambda ]}(\mathbb {R}^n\setminus \{0\})$
such that for every
$\widehat {\Phi }\in C^{n+1+[\Lambda ]}(\mathbb {R}^n\setminus \{0\})$
such that for every
 $|\tau |\leq n+1+[\Lambda ]$
, we have
$|\tau |\leq n+1+[\Lambda ]$
, we have  $$ \begin{align*}\partial^{\tau}\widehat{\Phi}=O(|\xi|^{-n-b})\quad \text{ as }|\xi|\to \infty.\end{align*} $$
$$ \begin{align*}\partial^{\tau}\widehat{\Phi}=O(|\xi|^{-n-b})\quad \text{ as }|\xi|\to \infty.\end{align*} $$
Lemma 3.8 [Reference Bui and Candy6, Theorem 1.1(i)]
Let
![]() $\nu \in \mathbb {R}$
,
$\nu \in \mathbb {R}$
,
![]() $0<p\leq \infty $
and
$0<p\leq \infty $
and
![]() $\zeta \geq 0$
with
$\zeta \geq 0$
with
![]() $\zeta>\nu /2-n/p$
. Assume that
$\zeta>\nu /2-n/p$
. Assume that
![]() $(1+|\cdot |)^\zeta \Phi \in L^1(\mathbb {R}^n)$
and
$(1+|\cdot |)^\zeta \Phi \in L^1(\mathbb {R}^n)$
and
![]() $\Phi $
satisfies (C1) and (C3) for
$\Phi $
satisfies (C1) and (C3) for
![]() $\Lambda =n/p$
,
$\Lambda =n/p$
,
![]() $r>\nu /2$
and
$r>\nu /2$
and
![]() $b>\Lambda -\nu /2$
. If
$b>\Lambda -\nu /2$
. If
![]() $f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^n)$
, there exists a polynomial g such that
$f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^n)$
, there exists a polynomial g such that
![]() $f-g$
is a distribution of growth
$f-g$
is a distribution of growth
![]() $\zeta $
and we have inequalities
$\zeta $
and we have inequalities
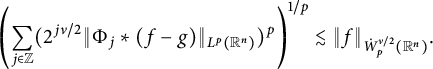 $$ \begin{align*}\left(\sum_{j\in \mathbb{Z}}(2^{j\nu/2}\|\Phi_j\ast(f-g)\|_{L^p(\mathbb{R}^n)})^p \right)^{1/p}\lesssim \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}.\end{align*} $$
$$ \begin{align*}\left(\sum_{j\in \mathbb{Z}}(2^{j\nu/2}\|\Phi_j\ast(f-g)\|_{L^p(\mathbb{R}^n)})^p \right)^{1/p}\lesssim \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}.\end{align*} $$
Lemma 3.9 [Reference Bui and Candy6, Theorem 5.3]
Let
![]() $0<p\leq \infty $
and
$0<p\leq \infty $
and
![]() $\nu \in \mathbb {R}$
. Let
$\nu \in \mathbb {R}$
. Let
![]() $\Lambda \geq 0$
and
$\Lambda \geq 0$
and
![]() $b_0> \Lambda -\nu /2$
. Assume
$b_0> \Lambda -\nu /2$
. Assume
![]() $(1+|\cdot |)^{-\zeta }f\in L^{\infty }$
with
$(1+|\cdot |)^{-\zeta }f\in L^{\infty }$
with
![]() $\zeta \geq 0$
. Suppose
$\zeta \geq 0$
. Suppose
![]() $\Phi \in L^{1}(\mathbb {R}^n)$
satisfies the (C2) with
$\Phi \in L^{1}(\mathbb {R}^n)$
satisfies the (C2) with
![]() $(1+|\cdot |)^{\zeta } \Phi (\cdot )\in L^1(\mathbb {R}^n)$
. Furthermore, assume that
$(1+|\cdot |)^{\zeta } \Phi (\cdot )\in L^1(\mathbb {R}^n)$
. Furthermore, assume that
![]() $\widehat {\Phi } \in C^{n+1+\max \{[\zeta ],[\Lambda ]\}}(\mathbb {R}^n\setminus \{0\})$
with
$\widehat {\Phi } \in C^{n+1+\max \{[\zeta ],[\Lambda ]\}}(\mathbb {R}^n\setminus \{0\})$
with
for
![]() $|\tau |\leq \max \{ [\Lambda ],[\zeta ]\}+1$
. If
$|\tau |\leq \max \{ [\Lambda ],[\zeta ]\}+1$
. If
![]() $\Lambda =n/p$
, then
$\Lambda =n/p$
, then
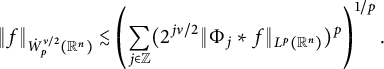 $$ \begin{align*}\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}\lesssim \left( \sum_{j\in \mathbb{Z}}(2^{j\nu/2}\|\Phi_j\ast f\|_{L^p(\mathbb{R}^n)})^p \right)^{1/p}.\end{align*} $$
$$ \begin{align*}\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}\lesssim \left( \sum_{j\in \mathbb{Z}}(2^{j\nu/2}\|\Phi_j\ast f\|_{L^p(\mathbb{R}^n)})^p \right)^{1/p}.\end{align*} $$
Theorem 3.10 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m+n/p$
,
$\alpha>n+m+n/p$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in \dot {W}_p^{\nu /2}(\mathbb {R}^n)$
with
$f\in \dot {W}_p^{\nu /2}(\mathbb {R}^n)$
with
![]() $p>1, \nu \in (0,2)$
and
$p>1, \nu \in (0,2)$
and
![]() $(1+|\cdot |)^{\zeta }f\in L^1(\mathbb {R}^n)$
with
$(1+|\cdot |)^{\zeta }f\in L^1(\mathbb {R}^n)$
with
![]() $\zeta>\max \{0,\nu /2-n/p\}$
. For
$\zeta>\max \{0,\nu /2-n/p\}$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f. Then
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f. Then
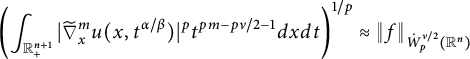 $$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)} \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)} \end{align} $$
and
 $$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} \approx\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} \approx\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
Proof Denote
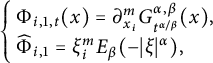 $$ \begin{align*} \begin{cases} &\hspace{-8pt}\Phi_{i,1,t}(x)= \partial^m_{x_{i}} G^{\alpha,\beta}_{t^{\alpha/\beta}}(x),\\ &\hspace{-8pt}\widehat{\Phi}_{i,1}=\xi_{i}^{m}E_\beta(-|\xi|^\alpha),\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}\Phi_{i,1,t}(x)= \partial^m_{x_{i}} G^{\alpha,\beta}_{t^{\alpha/\beta}}(x),\\ &\hspace{-8pt}\widehat{\Phi}_{i,1}=\xi_{i}^{m}E_\beta(-|\xi|^\alpha),\\ \end{cases} \end{align*} $$
where
![]() $\Phi _{1,t}(x)=t^{-n}\Phi _{1}(x/t)$
. Without loss of generality, for every
$\Phi _{1,t}(x)=t^{-n}\Phi _{1}(x/t)$
. Without loss of generality, for every
![]() $|\tau |\leq n+1+[\gamma ]$
and all
$|\tau |\leq n+1+[\gamma ]$
and all
![]() $\xi _j\in \{\xi _1,\xi _2,\ldots ,\xi _n\}$
, we just prove that
$\xi _j\in \{\xi _1,\xi _2,\ldots ,\xi _n\}$
, we just prove that
![]() $\xi _i^mE_{\beta }(-|\xi |^{\alpha })$
satisfies
$\xi _i^mE_{\beta }(-|\xi |^{\alpha })$
satisfies
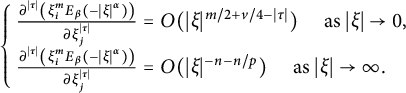 $$ \begin{align} \begin{cases} &\hspace{-8pt}\frac{\partial^{|\tau|}\left( \xi_i^mE_\beta(-|\xi|^\alpha) \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{m/2+v/4-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}\frac{\partial^{|\tau|}\left( \xi_i^mE_\beta(-|\xi|^\alpha) \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-n/p}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} &\hspace{-8pt}\frac{\partial^{|\tau|}\left( \xi_i^mE_\beta(-|\xi|^\alpha) \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{m/2+v/4-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}\frac{\partial^{|\tau|}\left( \xi_i^mE_\beta(-|\xi|^\alpha) \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-n/p}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align} $$
Case 1:
![]() $i\neq j$
.
$i\neq j$
.
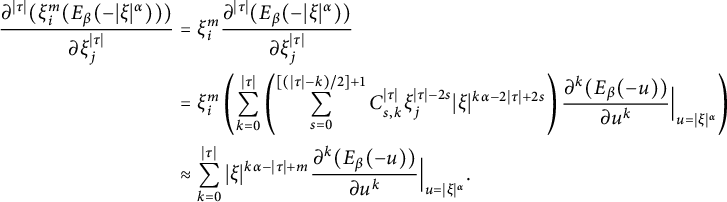 $$ \begin{align*} \frac{\partial^{|\tau|}(\xi_i^m (E_{\beta}(-|\xi|^\alpha)))}{\partial\xi_j^{|\tau|}}&=\xi_i^m\frac{\partial^{|\tau|}(E_{\beta}(-|\xi|^\alpha))}{\partial\xi_j^{|\tau|}} \\ &= \xi_i^m\left(\sum_{k=0}^{|\tau|}\left( \sum_{s=0}^{[(|\tau|-k)/2]+1}C^{|\tau|}_{s,k} \xi_j^{|\tau|-2s}|\xi|^{k\alpha-2|\tau|+2s}\right)\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &\approx \sum_{k=0}^{|\tau|}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
$$ \begin{align*} \frac{\partial^{|\tau|}(\xi_i^m (E_{\beta}(-|\xi|^\alpha)))}{\partial\xi_j^{|\tau|}}&=\xi_i^m\frac{\partial^{|\tau|}(E_{\beta}(-|\xi|^\alpha))}{\partial\xi_j^{|\tau|}} \\ &= \xi_i^m\left(\sum_{k=0}^{|\tau|}\left( \sum_{s=0}^{[(|\tau|-k)/2]+1}C^{|\tau|}_{s,k} \xi_j^{|\tau|-2s}|\xi|^{k\alpha-2|\tau|+2s}\right)\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &\approx \sum_{k=0}^{|\tau|}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
It follows from (2.6) that for
![]() $|\xi |$
in a neighborhood of
$|\xi |$
in a neighborhood of
![]() $0$
, we know
$0$
, we know
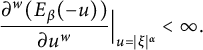 $$ \begin{align*}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}<\infty.\end{align*} $$
$$ \begin{align*}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}<\infty.\end{align*} $$
Since
![]() $\alpha>n+n/p+m$
, we get
$\alpha>n+n/p+m$
, we get
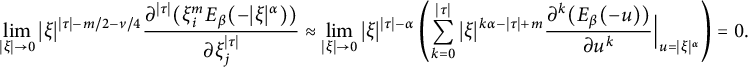 $$ \begin{align*}\lim\limits_{|\xi|\to 0} |\xi|^{|\tau|-m/2-v/4}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_j^{|\tau|}} \approx \lim\limits_{|\xi|\to 0}|\xi|^{|\tau|-\alpha}\left(\sum_{k=0}^{|\tau|}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}\right) =0.\end{align*} $$
$$ \begin{align*}\lim\limits_{|\xi|\to 0} |\xi|^{|\tau|-m/2-v/4}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_j^{|\tau|}} \approx \lim\limits_{|\xi|\to 0}|\xi|^{|\tau|-\alpha}\left(\sum_{k=0}^{|\tau|}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}\right) =0.\end{align*} $$
Then (2.5) and
![]() $\alpha>n+n/p+m$
imply
$\alpha>n+n/p+m$
imply
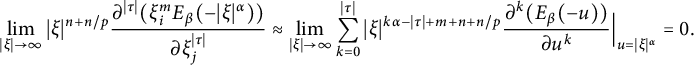 $$ \begin{align*} \lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_j^{|\tau|}}\approx\lim\limits_{|\xi|\to \infty} \sum_{k=0}^{|\tau|}|\xi|^{k\alpha-|\tau|+m+n+n/p}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}=0. \end{align*} $$
$$ \begin{align*} \lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_j^{|\tau|}}\approx\lim\limits_{|\xi|\to \infty} \sum_{k=0}^{|\tau|}|\xi|^{k\alpha-|\tau|+m+n+n/p}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}=0. \end{align*} $$
Case 2:
![]() $i=j$
. When
$i=j$
. When
![]() $m\geq | \tau |$
, we have
$m\geq | \tau |$
, we have
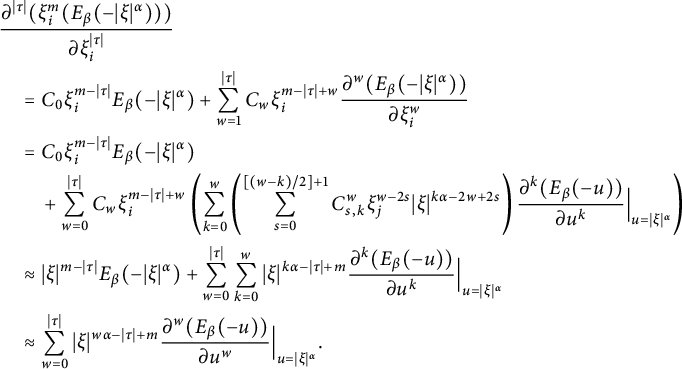 $$ \begin{align*} &\frac{\partial^{|\tau|}(\xi_i^m (E_{\beta}(-|\xi|^\alpha))) }{\partial\xi_i^{|\tau|}} \\ &\quad=C_0\xi_i^{m-|\tau|}E_\beta(-|\xi|^\alpha)+\sum_{w=1}^{|\tau|}C_w\xi_i^{m-|\tau|+w}\frac{\partial^w(E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^w}\\ &\quad= C_0 \xi_i^{m-|\tau|}E_\beta(-|\xi|^\alpha)\\&\qquad+\sum_{w=0}^{|\tau|}C_w\xi_i^{m-|\tau|+w}\left(\sum_{k=0}^{w}\left( \sum_{s=0}^{[(w-k)/2]+1}C^{w}_{s,k} \xi_j^{w-2s}|\xi|^{k\alpha-2w+2s}\right)\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &\quad\approx|\xi|^{m-|\tau|}E_\beta(-|\xi|^\alpha)+ \sum_{w=0}^{|\tau|}\sum_{k=0}^{w}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}\\ &\quad\approx \sum_{w=0}^{|\tau|}|\xi|^{w\alpha-|\tau|+m}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
$$ \begin{align*} &\frac{\partial^{|\tau|}(\xi_i^m (E_{\beta}(-|\xi|^\alpha))) }{\partial\xi_i^{|\tau|}} \\ &\quad=C_0\xi_i^{m-|\tau|}E_\beta(-|\xi|^\alpha)+\sum_{w=1}^{|\tau|}C_w\xi_i^{m-|\tau|+w}\frac{\partial^w(E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^w}\\ &\quad= C_0 \xi_i^{m-|\tau|}E_\beta(-|\xi|^\alpha)\\&\qquad+\sum_{w=0}^{|\tau|}C_w\xi_i^{m-|\tau|+w}\left(\sum_{k=0}^{w}\left( \sum_{s=0}^{[(w-k)/2]+1}C^{w}_{s,k} \xi_j^{w-2s}|\xi|^{k\alpha-2w+2s}\right)\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &\quad\approx|\xi|^{m-|\tau|}E_\beta(-|\xi|^\alpha)+ \sum_{w=0}^{|\tau|}\sum_{k=0}^{w}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}\\ &\quad\approx \sum_{w=0}^{|\tau|}|\xi|^{w\alpha-|\tau|+m}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
Then we have
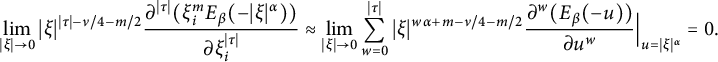 $$ \begin{align*}\lim\limits_{|\xi|\to 0} |\xi|^{|\tau|-\nu/4-m/2}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}} \approx \lim\limits_{|\xi|\to 0} \sum_{w=0}^{|\tau|}|\xi|^{w\alpha+m-\nu/4-m/2}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha} =0.\end{align*} $$
$$ \begin{align*}\lim\limits_{|\xi|\to 0} |\xi|^{|\tau|-\nu/4-m/2}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}} \approx \lim\limits_{|\xi|\to 0} \sum_{w=0}^{|\tau|}|\xi|^{w\alpha+m-\nu/4-m/2}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha} =0.\end{align*} $$
Since
![]() $\alpha>n+m+n/p$
and (2.5), we get
$\alpha>n+m+n/p$
and (2.5), we get
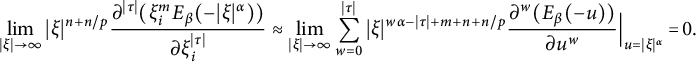 $$ \begin{align*} \lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}}\approx\lim\limits_{|\xi|\to \infty} \sum_{w=0}^{|\tau|}|\xi|^{w\alpha-|\tau|+m+n+n/p}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}\kern1.3pt{=}\kern1.3pt0.\end{align*} $$
$$ \begin{align*} \lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}}\approx\lim\limits_{|\xi|\to \infty} \sum_{w=0}^{|\tau|}|\xi|^{w\alpha-|\tau|+m+n+n/p}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}\kern1.3pt{=}\kern1.3pt0.\end{align*} $$
On the other hand, when
![]() $m<| \tau |$
, we can obtain
$m<| \tau |$
, we can obtain
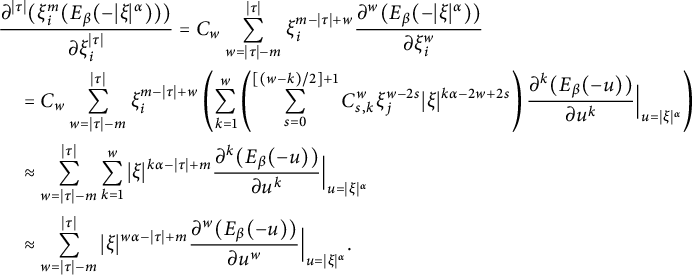 $$ \begin{align*} &\frac{\partial^{|\tau|}(\xi_i^m (E_{\beta}(-|\xi|^\alpha)))}{\partial\xi_i^{|\tau|}} = C_w\sum_{w=|\tau|-m}^{|\tau|}\xi_i^{m-|\tau|+w}\frac{\partial^{w}(E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{w}}\\ &\quad= C_w \sum_{w=|\tau|-m}^{|\tau|}\xi_i^{m-|\tau|+w}\left(\sum_{k=1}^{w}\left( \sum_{s=0}^{[(w-k)/2]+1}C^{w}_{s,k} \xi_j^{w-2s}|\xi|^{k\alpha-2w+2s}\right)\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\&\quad\approx \sum_{w=|\tau|-m}^{|\tau|}\sum_{k=1}^{w}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}\\&\quad\approx \sum_{w=|\tau|-m}^{|\tau|}|\xi|^{w\alpha-|\tau|+m}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
$$ \begin{align*} &\frac{\partial^{|\tau|}(\xi_i^m (E_{\beta}(-|\xi|^\alpha)))}{\partial\xi_i^{|\tau|}} = C_w\sum_{w=|\tau|-m}^{|\tau|}\xi_i^{m-|\tau|+w}\frac{\partial^{w}(E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{w}}\\ &\quad= C_w \sum_{w=|\tau|-m}^{|\tau|}\xi_i^{m-|\tau|+w}\left(\sum_{k=1}^{w}\left( \sum_{s=0}^{[(w-k)/2]+1}C^{w}_{s,k} \xi_j^{w-2s}|\xi|^{k\alpha-2w+2s}\right)\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\&\quad\approx \sum_{w=|\tau|-m}^{|\tau|}\sum_{k=1}^{w}|\xi|^{k\alpha-|\tau|+m}\frac{\partial^k(E_\beta(-u))}{\partial u^k}\Big|_{u=|\xi|^\alpha}\\&\quad\approx \sum_{w=|\tau|-m}^{|\tau|}|\xi|^{w\alpha-|\tau|+m}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
Moreover, we can get
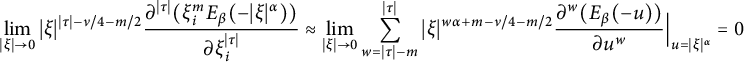 $$ \begin{align*}\lim\limits_{|\xi|\to 0} |\xi|^{|\tau|-\nu/4-m/2}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}} \approx \lim\limits_{|\xi|\to 0} \sum_{w=|\tau|-m}^{|\tau|}|\xi|^{w\alpha+m-\nu/4-m/2}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha} =0\end{align*} $$
$$ \begin{align*}\lim\limits_{|\xi|\to 0} |\xi|^{|\tau|-\nu/4-m/2}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}} \approx \lim\limits_{|\xi|\to 0} \sum_{w=|\tau|-m}^{|\tau|}|\xi|^{w\alpha+m-\nu/4-m/2}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha} =0\end{align*} $$
and
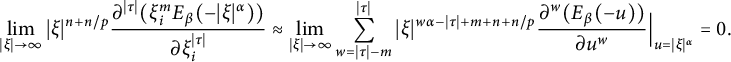 $$ \begin{align*}\lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}}\approx\lim\limits_{|\xi|\to \infty} \sum_{w=|\tau|-m}^{|\tau|}|\xi|^{w\alpha-|\tau|+m+n+n/p}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}=0.\end{align*} $$
$$ \begin{align*}\lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p}\frac{\partial^{|\tau|}(\xi_i^m E_{\beta}(-|\xi|^\alpha))}{\partial\xi_i^{|\tau|}}\approx\lim\limits_{|\xi|\to \infty} \sum_{w=|\tau|-m}^{|\tau|}|\xi|^{w\alpha-|\tau|+m+n+n/p}\frac{\partial^w(E_\beta(-u))}{\partial u^w}\Big|_{u=|\xi|^\alpha}=0.\end{align*} $$
By (3.12), when
![]() $r=m/2+\nu /4$
,
$r=m/2+\nu /4$
,
![]() $b=n/p$
and
$b=n/p$
and
![]() $b_{0}=n/p$
,
$b_{0}=n/p$
,
![]() $|\widehat {\Phi }_{1,i}|$
satisfies (C1), (C2), and (C3) in Lemmas 3.8 and 3.9. Thus, we know
$|\widehat {\Phi }_{1,i}|$
satisfies (C1), (C2), and (C3) in Lemmas 3.8 and 3.9. Thus, we know
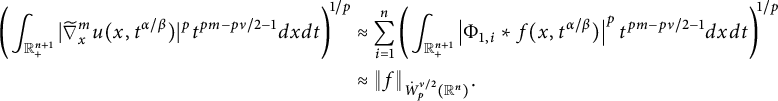 $$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{\kern-1.3pt1/p} &\approx \sum_{i=1}^{n}\left( \int_{\mathbb{R}_{+}^{n+1}} \left| \Phi_{1,i}\ast f(x,t^{\alpha/\beta})\right|^{p} t^{pm-p\nu/2-1}d{x}d{t} \right)^{\kern-1.3pt1/p}\notag\\ &\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}.\notag \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{\kern-1.3pt1/p} &\approx \sum_{i=1}^{n}\left( \int_{\mathbb{R}_{+}^{n+1}} \left| \Phi_{1,i}\ast f(x,t^{\alpha/\beta})\right|^{p} t^{pm-p\nu/2-1}d{x}d{t} \right)^{\kern-1.3pt1/p}\notag\\ &\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}.\notag \end{align*} $$
Below, we prove (3.11). For
![]() $\Phi _{2,t}(x)=t^{-n}\Phi _{2}(x/t)$
, we have
$\Phi _{2,t}(x)=t^{-n}\Phi _{2}(x/t)$
, we have
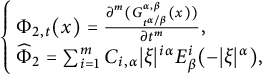 $$ \begin{align*} \begin{cases} &\hspace{-8pt}\Phi_{2,t}(x)= \frac{\partial^m(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x))}{\partial t^m} , \\&\hspace{-8pt}\widehat{\Phi}_2=\sum_{i=1}^{m}C_{i,\alpha}|\xi|^{i\alpha}E_\beta^i(-|\xi|^\alpha),\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}\Phi_{2,t}(x)= \frac{\partial^m(G^{\alpha,\beta}_{t^{\alpha/\beta}}(x))}{\partial t^m} , \\&\hspace{-8pt}\widehat{\Phi}_2=\sum_{i=1}^{m}C_{i,\alpha}|\xi|^{i\alpha}E_\beta^i(-|\xi|^\alpha),\\ \end{cases} \end{align*} $$
where
![]() $E_\beta ^i(-t)=\frac {d^i}{d t^i}(E_\beta (-t))$
. Similarly to
$E_\beta ^i(-t)=\frac {d^i}{d t^i}(E_\beta (-t))$
. Similarly to
![]() $\widehat {\Phi }_1$
, we just prove
$\widehat {\Phi }_1$
, we just prove
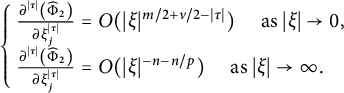 $$ \begin{align*} \begin{cases} &\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_2 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{m/2+\nu/2-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\&\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_2 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-n/p}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_2 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{m/2+\nu/2-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\&\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_2 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-n/p}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
By a direct calculation, we can obtain
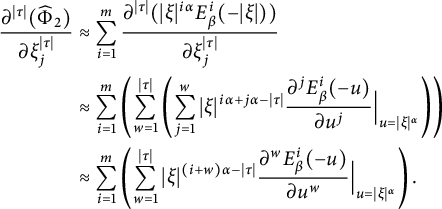 $$ \begin{align} \frac{\partial^{|\tau|}(\widehat{\Phi}_2)}{\partial \xi_j^{|\tau|}}&\approx \sum_{i=1}^{m} \frac{\partial^{|\tau|}(|\xi|^{i\alpha}E_\beta^i(-|\xi|))}{\partial \xi_j^{|\tau|}}\\ &\approx \sum_{i=1}^{m}\left(\sum_{w=1}^{|\tau|}\left( \sum_{j=1}^{w}|\xi|^{i\alpha+j\alpha-|\tau|} \frac{\partial^{j}E^i_\beta(-u)}{\partial u^{j}}\Big|_{u=|\xi|^\alpha}\right)\right)\notag\\ &\approx\sum_{i=1}^{m}\left(\sum_{w=1}^{|\tau|} |\xi|^{(i+w)\alpha-|\tau|} \frac{\partial^{w}E^i_\beta(-u)}{\partial u^{w}}\Big|_{u=|\xi|^\alpha}\right).\notag \end{align} $$
$$ \begin{align} \frac{\partial^{|\tau|}(\widehat{\Phi}_2)}{\partial \xi_j^{|\tau|}}&\approx \sum_{i=1}^{m} \frac{\partial^{|\tau|}(|\xi|^{i\alpha}E_\beta^i(-|\xi|))}{\partial \xi_j^{|\tau|}}\\ &\approx \sum_{i=1}^{m}\left(\sum_{w=1}^{|\tau|}\left( \sum_{j=1}^{w}|\xi|^{i\alpha+j\alpha-|\tau|} \frac{\partial^{j}E^i_\beta(-u)}{\partial u^{j}}\Big|_{u=|\xi|^\alpha}\right)\right)\notag\\ &\approx\sum_{i=1}^{m}\left(\sum_{w=1}^{|\tau|} |\xi|^{(i+w)\alpha-|\tau|} \frac{\partial^{w}E^i_\beta(-u)}{\partial u^{w}}\Big|_{u=|\xi|^\alpha}\right).\notag \end{align} $$
Then we can obtain
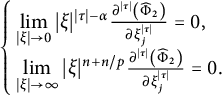 $$ \begin{align*} \begin{cases} &\hspace{-8pt}\lim\limits_{|\xi|\to 0}|\xi|^{|\tau|-\alpha} \frac{\partial^{|\tau|}\left( \widehat{\Phi}_2\right)}{\partial \xi_j^{|\tau|}} =0,\\ &\hspace{-8pt}\lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p} \frac{\partial^{|\tau|}\left(\widehat{\Phi}_2\right)}{\partial \xi_j^{|\tau|}} =0.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}\lim\limits_{|\xi|\to 0}|\xi|^{|\tau|-\alpha} \frac{\partial^{|\tau|}\left( \widehat{\Phi}_2\right)}{\partial \xi_j^{|\tau|}} =0,\\ &\hspace{-8pt}\lim\limits_{|\xi|\to \infty}|\xi|^{n+n/p} \frac{\partial^{|\tau|}\left(\widehat{\Phi}_2\right)}{\partial \xi_j^{|\tau|}} =0.\\ \end{cases} \end{align*} $$
Similarly, when
![]() $r=m/2+\nu /4$
,
$r=m/2+\nu /4$
,
![]() $b=n/p$
and
$b=n/p$
and
![]() $b_{0}=n/p$
,
$b_{0}=n/p$
,
![]() $|\widehat {\Phi }_{2}|$
satisfies (C1), (C2), and (C3) in Lemmas 3.8 and 3.9. Hence, we have
$|\widehat {\Phi }_{2}|$
satisfies (C1), (C2), and (C3) in Lemmas 3.8 and 3.9. Hence, we have
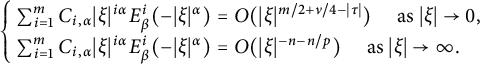 $$ \begin{align*} \begin{cases} &\hspace{-8pt}\sum_{i=1}^{m}C_{i,\alpha}|\xi|^{i\alpha}E_\beta^i(-|\xi|^\alpha) =O(|\xi|^{m/2+\nu/4-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}\sum_{i=1}^{m}C_{i,\alpha}|\xi|^{i\alpha}E_\beta^i(-|\xi|^\alpha) =O(|\xi|^{-n-n/p}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}\sum_{i=1}^{m}C_{i,\alpha}|\xi|^{i\alpha}E_\beta^i(-|\xi|^\alpha) =O(|\xi|^{m/2+\nu/4-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}\sum_{i=1}^{m}C_{i,\alpha}|\xi|^{i\alpha}E_\beta^i(-|\xi|^\alpha) =O(|\xi|^{-n-n/p}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
Similarly, by Lemmas 3.8 and 3.9, we know
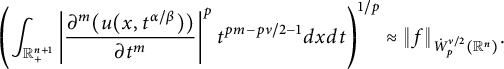 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^m(u(x,{t^{\alpha/\beta}}))}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} \approx\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}.\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^m(u(x,{t^{\alpha/\beta}}))}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} \approx\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}.\end{align*} $$
For a compact set
![]() $K\subset \mathbb {R}^{n}$
, the fractional-Sobolev capacity
$K\subset \mathbb {R}^{n}$
, the fractional-Sobolev capacity
![]() $C^{p}_\nu (K)$
is defined as
$C^{p}_\nu (K)$
is defined as
and for any set
![]() $E\subset \mathbb R^{n}$
, one defines
$E\subset \mathbb R^{n}$
, one defines
where
![]() $1_E$
denotes the characteristic function of E. Let
$1_E$
denotes the characteristic function of E. Let
![]() $1_{O}$
denote the characteristic function of the set O. In [Reference Li, Hu and Zhai28], Li, Hu, and Zhai obtained the following results.
$1_{O}$
denote the characteristic function of the set O. In [Reference Li, Hu and Zhai28], Li, Hu, and Zhai obtained the following results.
Lemma 3.11 [Reference Li, Hu and Zhai28, Theorem 3.2]
Let
![]() $\nu \in (0,2)$
,
$\nu \in (0,2)$
,
![]() $1\leq p<2n/\nu $
and
$1\leq p<2n/\nu $
and
![]() $f\in C^{\infty }_0(\mathbb {R}^n)$
. The following statements are equivalent.
$f\in C^{\infty }_0(\mathbb {R}^n)$
. The following statements are equivalent.
-
(i) The analytic inequality:
(3.14)where $$ \begin{align} \left(\int_{0}^{\infty}(V(O_t(f)))^{(2n-p\nu)/(2n)}dt^p \right)^{1/p}\lesssim ||f||_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}, \end{align} $$
$$ \begin{align} \left(\int_{0}^{\infty}(V(O_t(f)))^{(2n-p\nu)/(2n)}dt^p \right)^{1/p}\lesssim ||f||_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}, \end{align} $$
 $O_t(f):=\{x\in \mathbb {R}^n:|f(x)|>t\}$
and
$O_t(f):=\{x\in \mathbb {R}^n:|f(x)|>t\}$
and
 $V(O_t):= \int _{\mathbb {R}^n} 1_{O_t}dx$
.
$V(O_t):= \int _{\mathbb {R}^n} 1_{O_t}dx$
.
-
(ii) The fractional Sobolev inequality:
(3.15) $$ \begin{align} \left( \int_{\mathbb{R}^n}\frac{|f(x)|^p}{|x|^{p\nu/2}}dx\right)^{1/p} \lesssim ||f||_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}\frac{|f(x)|^p}{|x|^{p\nu/2}}dx\right)^{1/p} \lesssim ||f||_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
-
(iii) The fractional Hardy inequality:
(3.16) $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^{np/(n-p\nu/2)}d{x}\right)^{(n-p\nu/2)/np}\lesssim ||f||_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^{np/(n-p\nu/2)}d{x}\right)^{(n-p\nu/2)/np}\lesssim ||f||_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
-
(iv) For any bounded domain
 $O\subset \mathbb {R}^n$
with
$O\subset \mathbb {R}^n$
with
 $C^\infty $
boundary
$C^\infty $
boundary
 $\partial O$
, the iso-capacitary inequalities: (3.17)Moreover, (3.14), (3.15), (3.16), and (3.17) are all true.
$\partial O$
, the iso-capacitary inequalities: (3.17)Moreover, (3.14), (3.15), (3.16), and (3.17) are all true. $$ \begin{align} (V(O))^{1-p\nu/(2n)}\lesssim C^{p}_{\nu/2}(\overline{O}). \end{align} $$
$$ \begin{align} (V(O))^{1-p\nu/(2n)}\lesssim C^{p}_{\nu/2}(\overline{O}). \end{align} $$
Notice that the proof of (3.16) can be found in [Reference DiNezza, Palatucci and Valdinoci13, Reference Maz’ya and Shaposhnikova31]. For (3.15), readers can see [Reference Maz’ya and Shaposhnikova31] and the references therein.
Similarly to the inequalities involving fractional Laplacian in [Reference Hajaiej, Yu and Zhai21, Theorem 2.5 and Corollary 2.6], we will prove fractional logarithmic Gagliardo–Nirenberg inequalities which imply the
![]() $L^p$
-logarithmic Sobolev inequalities for
$L^p$
-logarithmic Sobolev inequalities for
![]() $\dot {W}^{\nu /2}_{p}(\mathbb R^{n}).$
$\dot {W}^{\nu /2}_{p}(\mathbb R^{n}).$
Theorem 3.12 Let
![]() $1<q<\infty $
,
$1<q<\infty $
,
![]() $0<\nu <2n$
,
$0<\nu <2n$
,
![]() $1<p<2n/\nu $
and
$1<p<2n/\nu $
and
![]() $f\in \dot {W}^{\nu /2}_{p}(\mathbb R^{n})\cap L^{q}(\mathbb {R}^n)$
with
$f\in \dot {W}^{\nu /2}_{p}(\mathbb R^{n})\cap L^{q}(\mathbb {R}^n)$
with
![]() $\|f\|_{L^{q}(\mathbb {R}^n)}>0.$
Then the following inequality holds.
$\|f\|_{L^{q}(\mathbb {R}^n)}>0.$
Then the following inequality holds.
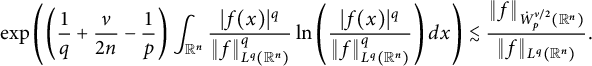 $$ \begin{align*}\exp\left(\left( \frac{1}{q}+\frac{\nu}{2n}-\frac{1}{p}\right)\int_{\mathbb{R}^n}\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}}\ln\left(\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}} \right)dx \right)\lesssim \frac{\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb R^{n})}}{\|f\|_{L^q(\mathbb{R}^n)}}.\end{align*} $$
$$ \begin{align*}\exp\left(\left( \frac{1}{q}+\frac{\nu}{2n}-\frac{1}{p}\right)\int_{\mathbb{R}^n}\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}}\ln\left(\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}} \right)dx \right)\lesssim \frac{\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb R^{n})}}{\|f\|_{L^q(\mathbb{R}^n)}}.\end{align*} $$
Proof Let
where
![]() $g(\cdot )$
is a convex function. For
$g(\cdot )$
is a convex function. For
![]() $h>h_1\geq 0$
, we can obtain
$h>h_1\geq 0$
, we can obtain
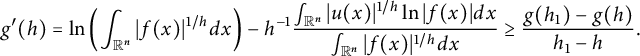 $$ \begin{align*}g'(h)= \ln\left(\int_{\mathbb{R}^n}|f(x)|^{1/h}dx \right)-h^{-1}\frac{\int_{\mathbb{R}^n}|u(x)|^{1/h}\ln|f(x)|dx}{\int_{\mathbb{R}^n}|f(x)|^{1/h}dx}\geq \frac{g(h_1)-g(h)}{h_1-h}.\end{align*} $$
$$ \begin{align*}g'(h)= \ln\left(\int_{\mathbb{R}^n}|f(x)|^{1/h}dx \right)-h^{-1}\frac{\int_{\mathbb{R}^n}|u(x)|^{1/h}\ln|f(x)|dx}{\int_{\mathbb{R}^n}|f(x)|^{1/h}dx}\geq \frac{g(h_1)-g(h)}{h_1-h}.\end{align*} $$
Taking
![]() $h=1/q$
,
$h=1/q$
,
![]() $h_1=1/p_{1}$
and
$h_1=1/p_{1}$
and
![]() $0<q<p_1\leq \infty $
, by [Reference Merker33, Lemma 1], we have
$0<q<p_1\leq \infty $
, by [Reference Merker33, Lemma 1], we have
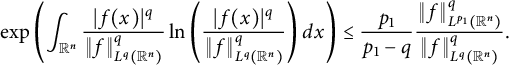 $$ \begin{align*} \exp\left( \int_{\mathbb{R}^n}\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}}\ln\left(\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}} \right)dx \right)\leq\frac{p_1}{p_1-q}\frac{\|f\|_{L^{p_1}(\mathbb{R}^n)}^q}{\|f\|_{L^q(\mathbb{R}^n)}^q}. \end{align*} $$
$$ \begin{align*} \exp\left( \int_{\mathbb{R}^n}\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}}\ln\left(\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}} \right)dx \right)\leq\frac{p_1}{p_1-q}\frac{\|f\|_{L^{p_1}(\mathbb{R}^n)}^q}{\|f\|_{L^q(\mathbb{R}^n)}^q}. \end{align*} $$
For
![]() $\gamma>0$
, Hölder’s inequality implies
$\gamma>0$
, Hölder’s inequality implies
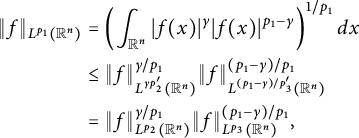 $$ \begin{align*} \|f\|_{L^{p_1}(\mathbb{R}^n)}&=\left( \int_{\mathbb{R}^n} |f(x)|^\gamma|f(x)|^{p_1-\gamma}\right)^{1/p_1}dx\\ &\leq \|f\|_{L^{\gamma p_2'}(\mathbb{R}^n)}^{\gamma/p_1}\|f\|_{L^{(p_1-\gamma)/p_3'}(\mathbb{R}^n)}^{(p_1-\gamma)/p_1}\\ &=\|f\|_{L^{ p_2}(\mathbb{R}^n)}^{\gamma/p_1}\|f\|_{L^{p_3}(\mathbb{R}^n)}^{(p_1-\gamma)/p_1}, \end{align*} $$
$$ \begin{align*} \|f\|_{L^{p_1}(\mathbb{R}^n)}&=\left( \int_{\mathbb{R}^n} |f(x)|^\gamma|f(x)|^{p_1-\gamma}\right)^{1/p_1}dx\\ &\leq \|f\|_{L^{\gamma p_2'}(\mathbb{R}^n)}^{\gamma/p_1}\|f\|_{L^{(p_1-\gamma)/p_3'}(\mathbb{R}^n)}^{(p_1-\gamma)/p_1}\\ &=\|f\|_{L^{ p_2}(\mathbb{R}^n)}^{\gamma/p_1}\|f\|_{L^{p_3}(\mathbb{R}^n)}^{(p_1-\gamma)/p_1}, \end{align*} $$
where
![]() $1/p_2'+1/p_3'=1$
,
$1/p_2'+1/p_3'=1$
,
![]() $p_2:=\gamma p_2'$
and
$p_2:=\gamma p_2'$
and
![]() $p_3:=(p_1-\gamma )/p_3'$
. By (3.16), for
$p_3:=(p_1-\gamma )/p_3'$
. By (3.16), for
![]() $1/p+(n-\nu /2)/n=1+1/p_2$
, we get
$1/p+(n-\nu /2)/n=1+1/p_2$
, we get
Then we can choose
![]() $p_1=nq/(n-q\nu /2) \in (q,\infty )$
for
$p_1=nq/(n-q\nu /2) \in (q,\infty )$
for
![]() $p_3=q$
,
$p_3=q$
,
![]() $\gamma $
and p satisfying
$\gamma $
and p satisfying
Hence,
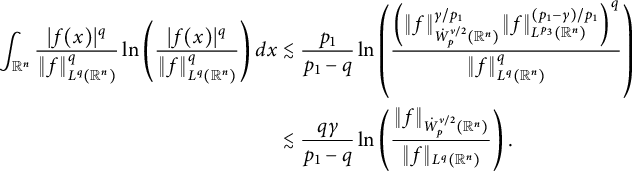 $$ \begin{align*} \int_{\mathbb{R}^n}\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}}\ln\left(\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}} \right)dx &\lesssim\frac{p_1}{p_1-q}\ln\left( \frac{\left(\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^{n})}^{\gamma/p_1}\|f\|_{L^{p_3}(\mathbb{R}^n)}^{(p_1-\gamma)/p_1} \right) ^q}{\|f\|_{L^q(\mathbb{R}^n)}^q}\right) \\ &\lesssim\frac{q\gamma}{p_1-q}\ln\left( \frac{\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^{n})}}{\|f\|_{L^q(\mathbb{R}^n)}}\right). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}}\ln\left(\frac{|f(x)|^q}{\|f\|^q_{L^q(\mathbb{R}^n)}} \right)dx &\lesssim\frac{p_1}{p_1-q}\ln\left( \frac{\left(\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^{n})}^{\gamma/p_1}\|f\|_{L^{p_3}(\mathbb{R}^n)}^{(p_1-\gamma)/p_1} \right) ^q}{\|f\|_{L^q(\mathbb{R}^n)}^q}\right) \\ &\lesssim\frac{q\gamma}{p_1-q}\ln\left( \frac{\|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^{n})}}{\|f\|_{L^q(\mathbb{R}^n)}}\right). \end{align*} $$
We can get
![]() $\frac {q\gamma }{p_1-q}=\frac {1}{{1}/{q}+{\nu }/{(2n)}-{1}/{p}}.$
$\frac {q\gamma }{p_1-q}=\frac {1}{{1}/{q}+{\nu }/{(2n)}-{1}/{p}}.$
When
![]() $p=q$
and
$p=q$
and
![]() $\|f\|_{L^q(\mathbb {R}^n)}=1$
, there holds the
$\|f\|_{L^q(\mathbb {R}^n)}=1$
, there holds the
![]() $L^p$
-logarithmic-type Sobolev inequality.
$L^p$
-logarithmic-type Sobolev inequality.
Corollary 3.13 Let
![]() $0<\nu <2n$
,
$0<\nu <2n$
,
![]() $1<p<2n/\nu $
,
$1<p<2n/\nu $
,
![]() $f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^{n})$
with
$f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^{n})$
with
![]() $\|f\|_{L^p(\mathbb {R}^n)}=1$
. Then
$\|f\|_{L^p(\mathbb {R}^n)}=1$
. Then
Let
![]() $f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^n)$
with
$f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^n)$
with
![]() $\nu \in (0,2)$
and
$\nu \in (0,2)$
and
![]() $(1+|\cdot |)^{\zeta }f\in L^1(\mathbb {R}^n)$
. Using (iii) of Lemma 3.11, we can obtain the following Sobolev-type trace inequality: for
$(1+|\cdot |)^{\zeta }f\in L^1(\mathbb {R}^n)$
. Using (iii) of Lemma 3.11, we can obtain the following Sobolev-type trace inequality: for
![]() $f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^n)$
with
$f\in \dot {W}^{\nu /2}_{p}(\mathbb {R}^n)$
with
![]() $p>1$
and
$p>1$
and
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f,
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f,
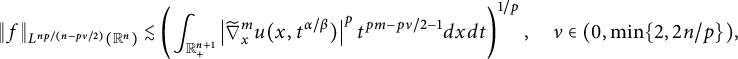 $$ \begin{align*} \|f\|_{L^{{np/(n-p\nu/2)}}(\mathbb{R}^n)}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})\right| ^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p},\quad\nu\in(0, \min\{ 2,2n/p \}), \end{align*} $$
$$ \begin{align*} \|f\|_{L^{{np/(n-p\nu/2)}}(\mathbb{R}^n)}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})\right| ^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p},\quad\nu\in(0, \min\{ 2,2n/p \}), \end{align*} $$
and
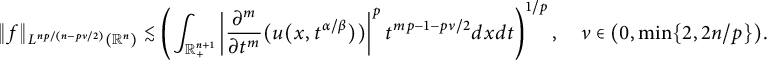 $$ \begin{align*} \|f\|_{L^{{np/(n-p\nu/2)}}(\mathbb{R}^n)}\lesssim \left(\int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^m}{\partial t^m}(u(x,{t^{\alpha/\beta}})) \right|^pt^{mp-1-p\nu/2} d{x}d{t}\right)^{1/p},\quad \nu\in(0, \min\{2, 2n/p\}). \end{align*} $$
$$ \begin{align*} \|f\|_{L^{{np/(n-p\nu/2)}}(\mathbb{R}^n)}\lesssim \left(\int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^m}{\partial t^m}(u(x,{t^{\alpha/\beta}})) \right|^pt^{mp-1-p\nu/2} d{x}d{t}\right)^{1/p},\quad \nu\in(0, \min\{2, 2n/p\}). \end{align*} $$
For
![]() $s=t^{\alpha /\beta }$
and (3.10), we can obtain
$s=t^{\alpha /\beta }$
and (3.10), we can obtain
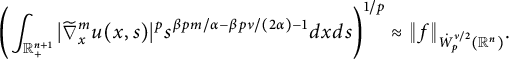 $$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-\beta p\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-\beta p\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
Notice that
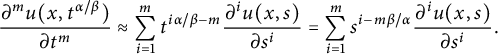 $$ \begin{align} \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \approx\sum_{i=1}^{m}t^{i\alpha/\beta-m}\frac{\partial^iu(x,s)}{\partial s^i}=\sum_{i=1}^{m}s^{i-m\beta/\alpha}\frac{\partial^iu(x,s)}{\partial s^i}. \end{align} $$
$$ \begin{align} \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \approx\sum_{i=1}^{m}t^{i\alpha/\beta-m}\frac{\partial^iu(x,s)}{\partial s^i}=\sum_{i=1}^{m}s^{i-m\beta/\alpha}\frac{\partial^iu(x,s)}{\partial s^i}. \end{align} $$
Then
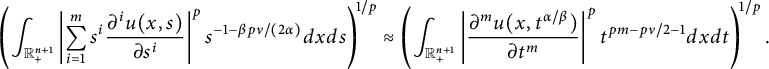 $$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m}s^{i}\frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{\kern-1.3pt{1}/{p}} &\approx \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^m u(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{\kern-1.3pt{1}/{p}}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m}s^{i}\frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{\kern-1.3pt{1}/{p}} &\approx \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^m u(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{\kern-1.3pt{1}/{p}}. \end{align*} $$
By (3.11), we can obtain
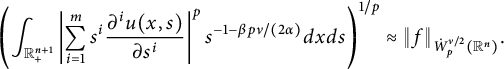 $$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m}s^{i}\frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{{1}/{p}} \approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m}s^{i}\frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{{1}/{p}} \approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb{R}^n)}. \end{align} $$
Moreover, based on Corollary 3.13 and (ii) of Lemma 3.11, applying (3.10) and (3.11), we can establish the logarithmic Sobolev trace inequalities for
![]() $\|f\|_{L^p(\mathbb {R}^n)}=1$
:
$\|f\|_{L^p(\mathbb {R}^n)}=1$
:
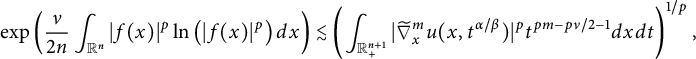 $$ \begin{align} \exp\left( \frac{\nu}{2n}\int_{\mathbb{R}^n}|f(x)|^{p}\ln\left(|f(x)|^{p} \right)dx \right)\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}, \end{align} $$
$$ \begin{align} \exp\left( \frac{\nu}{2n}\int_{\mathbb{R}^n}|f(x)|^{p}\ln\left(|f(x)|^{p} \right)dx \right)\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}, \end{align} $$
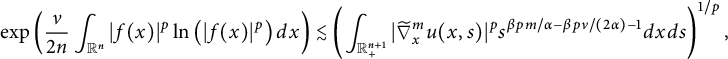 $$ \begin{align} \exp\left(\frac{\nu}{2n} \int_{\mathbb{R}^n}|f(x)|^{p}\ln\left(|f(x)|^{p} \right)dx \right)\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-\beta p\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}, \end{align} $$
$$ \begin{align} \exp\left(\frac{\nu}{2n} \int_{\mathbb{R}^n}|f(x)|^{p}\ln\left(|f(x)|^{p} \right)dx \right)\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-\beta p\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}, \end{align} $$
and the Hardy-type trace inequalities:
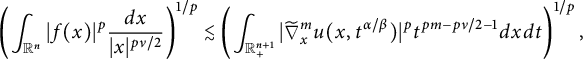 $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p} \lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}, \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p} \lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}, \end{align} $$
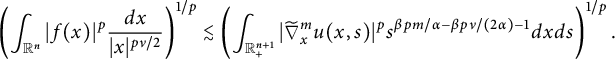 $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-\beta p\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-\beta p\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
Furthermore, the right-hand side of (3.21) and (3.23) can be replaced by
 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}}.\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}}.\end{align*} $$
The right-hand side of (3.22) and (3.24) can be replaced by
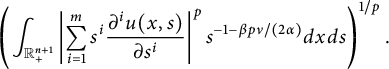 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m} s^i \frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{{1}/{p}}.\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m} s^i \frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{{1}/{p}}.\end{align*} $$
Therefore, Theorems 3.1 and 3.3 can be generalized to
![]() $p>1.$
$p>1.$
As a direct consequence of Lemma 3.11 and Corollary 3.13, we can use (3.10) and (3.11) to deduce the following results.
Corollary 3.14 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m+n/p$
,
$\alpha>n+m+n/p$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $\nu \in (0,2)$
,
$\nu \in (0,2)$
,
![]() $1< p<2n/\nu $
and
$1< p<2n/\nu $
and
![]() $f\in C^{\infty }_0(\mathbb {R}^n)$
. For
$f\in C^{\infty }_0(\mathbb {R}^n)$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f. The following statements are equivalent.
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f. The following statements are equivalent.
-
(i) The analytic inequality:
(3.25) $$ \begin{align} \left(\int_{0}^{\infty}(V(O_t(f)))^{(2n-p\nu)/(2n)}dt^p \right)^{1/p}\lesssim \left(\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left(\int_{0}^{\infty}(V(O_t(f)))^{(2n-p\nu)/(2n)}dt^p \right)^{1/p}\lesssim \left(\int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}. \end{align} $$
-
(ii) The fractional Sobolev trace inequality:
(3.26) $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^{np/(n-p\nu/2)}d{x}\right)^{(n-p\nu/2)/np}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^{np/(n-p\nu/2)}d{x}\right)^{(n-p\nu/2)/np}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}. \end{align} $$
-
(iii) The fractional Hardy inequality:
(3.27) $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p} \lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p} \lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p}. \end{align} $$
-
(iv) For any bounded domain
 $O\subset \mathbb {R}^n$
with
$O\subset \mathbb {R}^n$
with
 $C^\infty $
boundary
$C^\infty $
boundary
 $\partial O$
, the iso-capacitary inequalities: Moreover, (3.25), (3.26), and (3.27) are all true, and the right-hand side of (3.25), (3.26), and (3.27) can be replaced by
$\partial O$
, the iso-capacitary inequalities: Moreover, (3.25), (3.26), and (3.27) are all true, and the right-hand side of (3.25), (3.26), and (3.27) can be replaced by $$ \begin{align*}(V(O))^{1-p\nu/(2n)}\lesssim C^{p}_{\nu/2}(\overline{O}). \end{align*} $$
$$ \begin{align*}(V(O))^{1-p\nu/(2n)}\lesssim C^{p}_{\nu/2}(\overline{O}). \end{align*} $$
 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} .\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}} .\end{align*} $$
Proof If
![]() $f\in C^\infty _0(\mathbb R^{n})$
, we know
$f\in C^\infty _0(\mathbb R^{n})$
, we know
![]() $(1+|\cdot |)^\zeta f\in L^1(\mathbb {R}^n)$
. By (3.10) and (3.11), we have
$(1+|\cdot |)^\zeta f\in L^1(\mathbb {R}^n)$
. By (3.10) and (3.11), we have
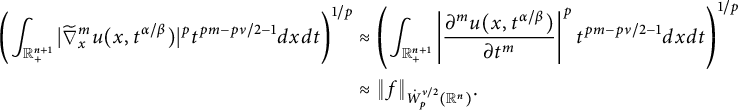 $$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p} &\approx \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}}\\ & \approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb R^{n})}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,t^{\alpha/\beta})|^pt^{pm-p\nu/2-1}d{x}d{t} \right)^{1/p} &\approx \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \frac{\partial^mu(x,{t^{\alpha/\beta}})}{\partial t^m} \right|^pt^{pm-p\nu/2-1} d{x}d{t}\right) ^{{1}/{p}}\\ & \approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb R^{n})}. \end{align*} $$
Then Corollary 3.14 follows from Lemma 3.11 and Corollary 3.13.
Corollary 3.15 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m+n/p$
,
$\alpha>n+m+n/p$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $\nu \in (0,2)$
,
$\nu \in (0,2)$
,
![]() $1< p<2n/\nu $
and
$1< p<2n/\nu $
and
![]() $f\in C^{\infty }_0(\mathbb {R}^n)$
. For
$f\in C^{\infty }_0(\mathbb {R}^n)$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f. The following statements are equivalent.
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the time-space fractional extension of f. The following statements are equivalent.
-
(i) The analytic inequality:
(3.28) $$ \begin{align} \left(\int_{0}^{\infty}(V(O_t(f)))^{(2n-p\nu)/(2n)}dt^p \right)^{1/p} \lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left(\int_{0}^{\infty}(V(O_t(f)))^{(2n-p\nu)/(2n)}dt^p \right)^{1/p} \lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
-
(ii) The fractional Sobolev inequality:
(3.29) $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^{np/(n-p\nu/2)}d{x}\right)^{(n-p\nu/2)/np} \lesssim\left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^{np/(n-p\nu/2)}d{x}\right)^{(n-p\nu/2)/np} \lesssim\left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
-
(iii) The fractional Hardy inequality:
(3.30) $$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}^n}|f(x)|^p\frac{d{x}}{|x|^{p\nu/2}}\right)^{1/p}\lesssim \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{1/p}. \end{align} $$
-
(iv) For any bounded domain
 $O\subset \mathbb {R}^n$
with
$O\subset \mathbb {R}^n$
with
 $C^\infty $
boundary
$C^\infty $
boundary
 $\partial O$
, the iso-capacitary inequalities: Moreover, (3.28), (3.29), and (3.30) are all true, and the right-hand side of (3.28), (3.29), and (3.30) can be replaced by
$\partial O$
, the iso-capacitary inequalities: Moreover, (3.28), (3.29), and (3.30) are all true, and the right-hand side of (3.28), (3.29), and (3.30) can be replaced by $$ \begin{align*}(V(O))^{1-p\nu/(2n)}\lesssim C^{p}_{\nu/2}(\overline{O}). \end{align*} $$
$$ \begin{align*}(V(O))^{1-p\nu/(2n)}\lesssim C^{p}_{\nu/2}(\overline{O}). \end{align*} $$
 $$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m} s^i \frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{{1}/{p}}.\end{align*} $$
$$ \begin{align*}\left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m} s^i \frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{{1}/{p}}.\end{align*} $$
Proof By (3.18) and (3.20), we have
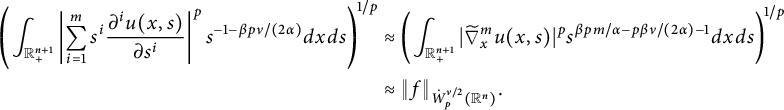 $$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m} s^i\frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{\kern-1.2pt{1}/{p}}&\approx \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{\kern-1.2pt1/p}\\ &\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb R^{n})}. \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}}\left| \sum_{i=1}^{m} s^i\frac{\partial^iu(x,s)}{\partial s^i} \right|^ps^{-1-\beta p\nu/(2\alpha)} d{x}d{s}\right) ^{\kern-1.2pt{1}/{p}}&\approx \left( \int_{\mathbb{R}_{+}^{n+1}}|\widetilde{\nabla}_x^m u(x,s)|^ps^{\beta pm/\alpha-p\beta\nu/(2\alpha)-1}d{x}d{s} \right)^{\kern-1.2pt1/p}\\ &\approx \|f\|_{\dot{W}^{\nu/2}_{p}(\mathbb R^{n})}. \end{align*} $$
4 Sobolev affine trace inequalities
Definition 4.1 Assume that
![]() $\sigma $
:
$\sigma $
:
![]() $\mathbb {R}^{n+1}_+\to \mathbb {R}_+$
is a positive measurable function. Denote by
$\mathbb {R}^{n+1}_+\to \mathbb {R}_+$
is a positive measurable function. Denote by
![]() $L^p(\mathbb {R}_+^{n+1},\sigma )$
the weighted Lebesgue space of all measurable functions
$L^p(\mathbb {R}_+^{n+1},\sigma )$
the weighted Lebesgue space of all measurable functions
![]() $f: \mathbb {R}_+^{n+1}\to \mathbb {R}$
with
$f: \mathbb {R}_+^{n+1}\to \mathbb {R}$
with
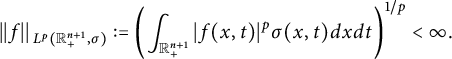 $$ \begin{align*}\left| \left| f\right| \right|{}_{L^p(\mathbb{R}^{n+1}_+,\sigma)}:=\left( \int_{\mathbb{R}_{+}^{n+1}}|f(x,t)|^p\sigma(x,t)dxdt\right)^{1/p} <\infty.\end{align*} $$
$$ \begin{align*}\left| \left| f\right| \right|{}_{L^p(\mathbb{R}^{n+1}_+,\sigma)}:=\left( \int_{\mathbb{R}_{+}^{n+1}}|f(x,t)|^p\sigma(x,t)dxdt\right)^{1/p} <\infty.\end{align*} $$
Define
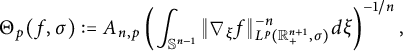 $$ \begin{align*}\Theta_p(f,\sigma):=A_{n,p}\left( \int_{\mathbb{S}^{n-1}}\|\nabla_{\xi}f\|^{-n}_{L^p(\mathbb{R}^{n+1}_+,\sigma)}d\xi\right)^{-1/n},\end{align*} $$
$$ \begin{align*}\Theta_p(f,\sigma):=A_{n,p}\left( \int_{\mathbb{S}^{n-1}}\|\nabla_{\xi}f\|^{-n}_{L^p(\mathbb{R}^{n+1}_+,\sigma)}d\xi\right)^{-1/n},\end{align*} $$
where
![]() $A_{n,p}$
is a constant depending on
$A_{n,p}$
is a constant depending on
![]() $n,p$
.
$n,p$
.
The following affine Sobolev-type inequality was obtained in Haddad, Jiménez, and Montenegro [Reference Haddad, Jiménez and Montenegro20].
Theorem 4.2 [Reference Haddad, Jiménez and Montenegro20, Theorem 1.1]
Define a function
![]() $\sigma $
on
$\sigma $
on
![]() $\mathbb {R}^{n+1}_+$
as
$\mathbb {R}^{n+1}_+$
as
![]() $\sigma (x,t):=t^\gamma \, \forall \,(x,t)\in \mathbb {R}_+^{n+1}$
. Let
$\sigma (x,t):=t^\gamma \, \forall \,(x,t)\in \mathbb {R}_+^{n+1}$
. Let
![]() $\gamma \geq 0$
,
$\gamma \geq 0$
,
![]() $1\leq p<n+\gamma +1$
and
$1\leq p<n+\gamma +1$
and
![]() $p^*_\gamma =p(n+\gamma +1)/(n+\gamma +1-p)$
. There exists a sharp constant
$p^*_\gamma =p(n+\gamma +1)/(n+\gamma +1-p)$
. There exists a sharp constant
![]() $J(n,p,\gamma )$
such that
$J(n,p,\gamma )$
such that
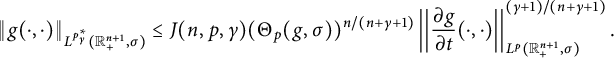 $$ \begin{align} \|g(\cdot,\cdot)\|_{L^{p^*_\gamma}(\mathbb{R}^{n+1}_+,\sigma)}\leq J(n,p,\gamma)(\Theta_p(g,\sigma))^{n/(n+\gamma+1)}\left| \left| \frac{\partial g}{\partial t}(\cdot,\cdot)\right| \right| ^{(\gamma+1)/(n+\gamma+1)}_{L^p(\mathbb{R}^{n+1}_+,\sigma)}. \end{align} $$
$$ \begin{align} \|g(\cdot,\cdot)\|_{L^{p^*_\gamma}(\mathbb{R}^{n+1}_+,\sigma)}\leq J(n,p,\gamma)(\Theta_p(g,\sigma))^{n/(n+\gamma+1)}\left| \left| \frac{\partial g}{\partial t}(\cdot,\cdot)\right| \right| ^{(\gamma+1)/(n+\gamma+1)}_{L^p(\mathbb{R}^{n+1}_+,\sigma)}. \end{align} $$
Moreover, in (4.1), the equality holds if
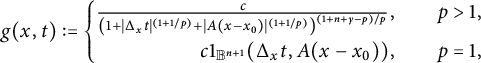 $$ \begin{align*} g(x,t):= \begin{cases} \frac{c}{\left( 1+|\Delta_x t|^{(1+1/p)}+|A(x-x_0)|^{(1+1/p)}\right) ^{(1+n+\gamma-p)/p}},&\quad p>1,\\ \qquad\qquad\quad c1_{\mathbb{B}^{n+1}}(\Delta_x t, A(x-x_0)),&\quad p=1, \end{cases} \end{align*} $$
$$ \begin{align*} g(x,t):= \begin{cases} \frac{c}{\left( 1+|\Delta_x t|^{(1+1/p)}+|A(x-x_0)|^{(1+1/p)}\right) ^{(1+n+\gamma-p)/p}},&\quad p>1,\\ \qquad\qquad\quad c1_{\mathbb{B}^{n+1}}(\Delta_x t, A(x-x_0)),&\quad p=1, \end{cases} \end{align*} $$
where
![]() $(c,|\Delta _x|,x_0,A)\in \mathbb {R}\times \mathbb {R}_+\times \mathbb {R}^n\times GL_n$
. and
$(c,|\Delta _x|,x_0,A)\in \mathbb {R}\times \mathbb {R}_+\times \mathbb {R}^n\times GL_n$
. and
![]() $1_{\mathbb {B}^{n+1}}$
is the characteristic function of the unit ball in
$1_{\mathbb {B}^{n+1}}$
is the characteristic function of the unit ball in
![]() $\mathbb {R}^{n+1}$
and
$\mathbb {R}^{n+1}$
and
![]() $GL_n$
denotes the set of all invertible real
$GL_n$
denotes the set of all invertible real
![]() $n\times n$
-matrices.
$n\times n$
-matrices.
Motivated by Lombardi and Xiao [Reference Lombardi and Xiao30], we establish the following affine trace inequality.
Theorem 4.3 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n$
,
$\alpha>n$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $f\in C^\infty _0(\mathbb {R}^n)$
and its time-space fractional extension
$f\in C^\infty _0(\mathbb {R}^n)$
and its time-space fractional extension
![]() $u(x,t ):=G_{t}^{\alpha ,\beta }*f(x)\ \forall \ (x,t)\in \mathbb R^{n+1}_{+}$
when
$u(x,t ):=G_{t}^{\alpha ,\beta }*f(x)\ \forall \ (x,t)\in \mathbb R^{n+1}_{+}$
when
![]() $\nu \geq 1$
. For
$\nu \geq 1$
. For
![]() $p=\frac {2(n+\nu +2m)}{n+\nu +2+2m}$
and
$p=\frac {2(n+\nu +2m)}{n+\nu +2+2m}$
and
![]() $\nu \geq 1-2m$
, there holds
$\nu \geq 1-2m$
, there holds
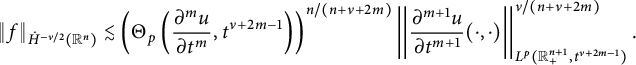 $$ \begin{align*}\|f\|_{\dot{H}^{-\nu/2}(\mathbb{R}^n)}\lesssim \left( \Theta_p\left( \frac{\partial^{m}u}{\partial t^{m}},t^{\nu+2m-1}\right) \right) ^{{n/(n+\nu+2m)}}\left| \left| \frac{\partial^{m+1} u}{\partial t^{m+1}}(\cdot,\cdot)\right| \right| ^{{\nu/(n+\nu+2m)}}_{L^p(\mathbb{R}^{n+1}_+,t^{\nu+2m-1})}\notag.\end{align*} $$
$$ \begin{align*}\|f\|_{\dot{H}^{-\nu/2}(\mathbb{R}^n)}\lesssim \left( \Theta_p\left( \frac{\partial^{m}u}{\partial t^{m}},t^{\nu+2m-1}\right) \right) ^{{n/(n+\nu+2m)}}\left| \left| \frac{\partial^{m+1} u}{\partial t^{m+1}}(\cdot,\cdot)\right| \right| ^{{\nu/(n+\nu+2m)}}_{L^p(\mathbb{R}^{n+1}_+,t^{\nu+2m-1})}\notag.\end{align*} $$
Proof From (ii) and (iii) of Lemma 2.5, we know
when
![]() $2m-1<\gamma <2m+2\alpha -1$
. Let
$2m-1<\gamma <2m+2\alpha -1$
. Let
![]() $\gamma =\nu +2m-1\in (2m-1,2m+2\alpha -1)$
. By Theorem 4.2, we can obtain
$\gamma =\nu +2m-1\in (2m-1,2m+2\alpha -1)$
. By Theorem 4.2, we can obtain
![]() $\sigma :=t^\gamma =t^{\nu +2m-1}$
and
$\sigma :=t^\gamma =t^{\nu +2m-1}$
and
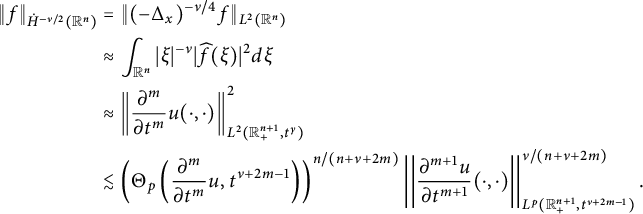 $$ \begin{align*} \|f\|_{\dot{H}^{-\nu/2}(\mathbb{R}^n)}&=\|(-\Delta_x)^{-\nu/4}f\|_{L^2(\mathbb{R}^n)}\notag\\ &\approx\int_{\mathbb{R}^n}|\xi|^{-\nu}|\widehat{f}(\xi)|^2d{\xi}\notag\\ &\approx\left\| \frac{\partial^m}{\partial t^m}u(\cdot{},\cdot{})\right\| ^2_{L^2(\mathbb{R}_+^{n+1},t^\gamma)}\notag\\ &\lesssim \left( \Theta_p\left( \frac{\partial^{m} }{\partial t^{m}}u,t^{\nu+2m-1}\right) \right) ^{{n/(n+\nu+2m)}}\left| \left| \frac{\partial^{m+1} u}{\partial t^{m+1}}(\cdot,\cdot)\right| \right| ^{{\nu/(n+\nu+2m)}}_{L^p(\mathbb{R}^{n+1}_+,t^{\nu+2m-1})}\notag. \end{align*} $$
$$ \begin{align*} \|f\|_{\dot{H}^{-\nu/2}(\mathbb{R}^n)}&=\|(-\Delta_x)^{-\nu/4}f\|_{L^2(\mathbb{R}^n)}\notag\\ &\approx\int_{\mathbb{R}^n}|\xi|^{-\nu}|\widehat{f}(\xi)|^2d{\xi}\notag\\ &\approx\left\| \frac{\partial^m}{\partial t^m}u(\cdot{},\cdot{})\right\| ^2_{L^2(\mathbb{R}_+^{n+1},t^\gamma)}\notag\\ &\lesssim \left( \Theta_p\left( \frac{\partial^{m} }{\partial t^{m}}u,t^{\nu+2m-1}\right) \right) ^{{n/(n+\nu+2m)}}\left| \left| \frac{\partial^{m+1} u}{\partial t^{m+1}}(\cdot,\cdot)\right| \right| ^{{\nu/(n+\nu+2m)}}_{L^p(\mathbb{R}^{n+1}_+,t^{\nu+2m-1})}\notag. \end{align*} $$
Theorem 4.3 suggests
which can be generalized as follows.
Theorem 4.4 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m+n/p,\ p>1,\ \beta \in (0,1],\ t>0,\ f\in \dot {W}_p^{-\nu /2}(\mathbb {R}^n)$
with
$\alpha>n+m+n/p,\ p>1,\ \beta \in (0,1],\ t>0,\ f\in \dot {W}_p^{-\nu /2}(\mathbb {R}^n)$
with
![]() $\nu \in (0,2)$
and
$\nu \in (0,2)$
and
![]() $(1+|\cdot |)^{\zeta }f\in L^1(\mathbb {R}^n)$
with
$(1+|\cdot |)^{\zeta }f\in L^1(\mathbb {R}^n)$
with
![]() $\zeta>\max \{0,\nu /2-n/p\}.$
For
$\zeta>\max \{0,\nu /2-n/p\}.$
For
![]() ${(x,t)\in \mathbb R^{n}\times (0,\infty )}$
, denote by
${(x,t)\in \mathbb R^{n}\times (0,\infty )}$
, denote by
![]() $u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the extension of f via the time-space fractional heat kernel. Then
$u(x,t)=G^{\alpha ,\beta }_{t}*f(x)$
the extension of f via the time-space fractional heat kernel. Then
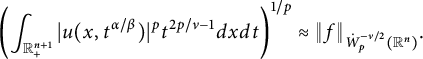 $$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}} |u(x,t^{{\alpha/\beta}})|^p t^{2p/\nu-1}d{x}d{t} \right) ^{1/p}\approx \|f\|_{\dot{W}^{-\nu/2}_{p}(\mathbb{R}^n)}.\end{align} $$
$$ \begin{align} \left( \int_{\mathbb{R}_{+}^{n+1}} |u(x,t^{{\alpha/\beta}})|^p t^{2p/\nu-1}d{x}d{t} \right) ^{1/p}\approx \|f\|_{\dot{W}^{-\nu/2}_{p}(\mathbb{R}^n)}.\end{align} $$
Proof Let
![]() $\Phi _{3,t}(x)=t^{-n}\Phi _{3}(x/t)$
. Similarly to the proof of Theorem 3.10, for every
$\Phi _{3,t}(x)=t^{-n}\Phi _{3}(x/t)$
. Similarly to the proof of Theorem 3.10, for every
![]() $\xi _j\in \{\xi _1,\xi _2,\ldots ,\xi _n\}$
, we just prove
$\xi _j\in \{\xi _1,\xi _2,\ldots ,\xi _n\}$
, we just prove
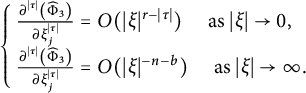 $$ \begin{align*} \begin{cases} &\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_3 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{r-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_3 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-b}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_3 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{r-|\tau|}) \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}\frac{\partial^{|\tau|}\left(\widehat{\Phi}_3 \right)}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-b}) \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
By (3.13), we can obtain
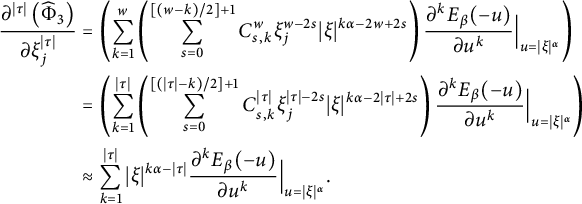 $$ \begin{align*} \frac{\partial^{|\tau|}\left(\widehat{\Phi}_3 \right)}{\partial \xi_j^{|\tau|}}&=\left(\sum_{k=1}^{w}\left( \sum_{s=0}^{[(w-k)/2]+1}C^{w}_{s,k} \xi_j^{w-2s}|\xi|^{k\alpha-2w+2s}\right)\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &= \left(\sum_{k=1}^{|\tau|}\left( \sum_{s=0}^{[(|\tau|-k)/2]+1}C^{|\tau|}_{s,k} \xi_j^{|\tau|-2s}|\xi|^{k\alpha-2|\tau|+2s}\right)\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &\approx \sum_{k=1}^{|\tau|}|\xi|^{k\alpha-|\tau|}\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
$$ \begin{align*} \frac{\partial^{|\tau|}\left(\widehat{\Phi}_3 \right)}{\partial \xi_j^{|\tau|}}&=\left(\sum_{k=1}^{w}\left( \sum_{s=0}^{[(w-k)/2]+1}C^{w}_{s,k} \xi_j^{w-2s}|\xi|^{k\alpha-2w+2s}\right)\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &= \left(\sum_{k=1}^{|\tau|}\left( \sum_{s=0}^{[(|\tau|-k)/2]+1}C^{|\tau|}_{s,k} \xi_j^{|\tau|-2s}|\xi|^{k\alpha-2|\tau|+2s}\right)\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha} \right)\\ &\approx \sum_{k=1}^{|\tau|}|\xi|^{k\alpha-|\tau|}\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha}. \end{align*} $$
Using (2.6), for
![]() $|\xi |$
in a neighborhood of
$|\xi |$
in a neighborhood of
![]() $0$
, we know
$0$
, we know
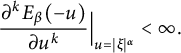 $$ \begin{align*}\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha}<\infty.\end{align*} $$
$$ \begin{align*}\frac{\partial^kE_\beta(-u)}{\partial u^k}\Big|_{u=|\xi|^\alpha}<\infty.\end{align*} $$
Take
![]() $r=\alpha $
. This indicates that
$r=\alpha $
. This indicates that
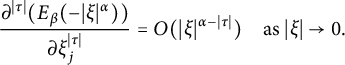 $$ \begin{align*}\frac{\partial^{|\tau|}(E_\beta(-|\xi|^\alpha))}{\partial \xi_j^{|\tau|}}=O(|\xi|^{\alpha-|\tau|})\quad \text{as }|\xi|\to0.\end{align*} $$
$$ \begin{align*}\frac{\partial^{|\tau|}(E_\beta(-|\xi|^\alpha))}{\partial \xi_j^{|\tau|}}=O(|\xi|^{\alpha-|\tau|})\quad \text{as }|\xi|\to0.\end{align*} $$
By (2.5), for
![]() $M>0$
, we know
$M>0$
, we know
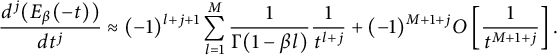 $$ \begin{align*} \frac{d^j(E_\beta(-t))}{d t^j}\approx (-1)^{l+j+1}\sum_{l=1}^{M}\frac{1}{\Gamma(1-\beta l)}\frac{1}{t^{l+j}}+(-1)^{M+1+j}O\left[ \frac{1}{t^{M+1+j}}\right]. \end{align*} $$
$$ \begin{align*} \frac{d^j(E_\beta(-t))}{d t^j}\approx (-1)^{l+j+1}\sum_{l=1}^{M}\frac{1}{\Gamma(1-\beta l)}\frac{1}{t^{l+j}}+(-1)^{M+1+j}O\left[ \frac{1}{t^{M+1+j}}\right]. \end{align*} $$
So, for
![]() $b_0=b=n/p$
,
$b_0=b=n/p$
,
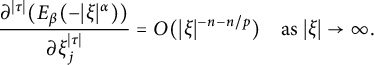 $$ \begin{align*}\frac{\partial^{|\tau|}(E_\beta(-|\xi|^\alpha))}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-n/p})\quad \text{as }|\xi|\to\infty.\end{align*} $$
$$ \begin{align*}\frac{\partial^{|\tau|}(E_\beta(-|\xi|^\alpha))}{\partial \xi_j^{|\tau|}}=O(|\xi|^{-n-n/p})\quad \text{as }|\xi|\to\infty.\end{align*} $$
If
![]() $|\tau |=0$
, for
$|\tau |=0$
, for
![]() $r=-\nu /4>-\nu /2$
and
$r=-\nu /4>-\nu /2$
and
![]() $b=b_0=n/p$
, we have
$b=b_0=n/p$
, we have
 $$ \begin{align*} \begin{cases} &\hspace{-8pt}E_\beta(-|\xi|^\alpha) =O(|\xi|^{r-|\tau|}), \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}E_\beta(-|\xi|^\alpha) =O(|\xi|^{-n-b}), \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\hspace{-8pt}E_\beta(-|\xi|^\alpha) =O(|\xi|^{r-|\tau|}), \quad \text{ as } |\xi| \to 0 ,\\ &\hspace{-8pt}E_\beta(-|\xi|^\alpha) =O(|\xi|^{-n-b}), \quad \text{ as } |\xi| \to \infty.\\ \end{cases} \end{align*} $$
Hence, by Lemmas 3.8 and 3.9, we can obtain
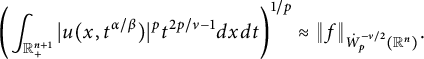 $$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}} |u(x,t^{{\alpha/\beta}})|^p t^{2p/\nu-1}d{x}d{t} \right) ^{1/p}\approx \|f\|_{\dot{W}^{-\nu/2}_{p}(\mathbb{R}^n)}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \left( \int_{\mathbb{R}_{+}^{n+1}} |u(x,t^{{\alpha/\beta}})|^p t^{2p/\nu-1}d{x}d{t} \right) ^{1/p}\approx \|f\|_{\dot{W}^{-\nu/2}_{p}(\mathbb{R}^n)}.\\[-42pt] \end{align*} $$
Then (4.2) and Theorem 4.2 imply that
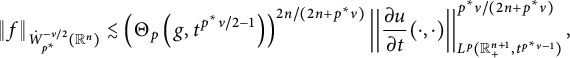 $$ \begin{align*}\|f\|_{\dot{W}^{-\nu/2}_{p^*}(\mathbb{R}^n)}\lesssim\left( \Theta_p\left( g,t^{p^*\nu/2-1}\right) \right) ^{2n/(2n+p^*\nu)}\left| \left| \frac{\partial u}{\partial t}(\cdot,\cdot)\right| \right| ^{p^*\nu/(2n+p^*\nu)}_{L^p(\mathbb{R}^{n+1}_+,t^{p^*\nu-1})},\end{align*} $$
$$ \begin{align*}\|f\|_{\dot{W}^{-\nu/2}_{p^*}(\mathbb{R}^n)}\lesssim\left( \Theta_p\left( g,t^{p^*\nu/2-1}\right) \right) ^{2n/(2n+p^*\nu)}\left| \left| \frac{\partial u}{\partial t}(\cdot,\cdot)\right| \right| ^{p^*\nu/(2n+p^*\nu)}_{L^p(\mathbb{R}^{n+1}_+,t^{p^*\nu-1})},\end{align*} $$
where
![]() $\nu \in (2/p^*,2n)$
,
$\nu \in (2/p^*,2n)$
,
![]() $1\leq p<n+p^*\nu /2$
with
$1\leq p<n+p^*\nu /2$
with
![]() $p^*$
satisfying
$p^*$
satisfying
![]() $p^*\geq \max \left \lbrace 2/\nu ,1 \right \rbrace $
and
$p^*\geq \max \left \lbrace 2/\nu ,1 \right \rbrace $
and
5 Local Sobolev-type trace inequalities
In this section, we prove (1.7) and (1.8) by the Carleson measure characterization of Q-type spaces
![]() $Q_{\kappa }(\mathbb R^{n})$
introduced in [Reference Dafni and Xiao11].
$Q_{\kappa }(\mathbb R^{n})$
introduced in [Reference Dafni and Xiao11].
Definition 5.1 For
![]() $0\leq \kappa <1$
,
$0\leq \kappa <1$
,
![]() $Q_{\kappa }(\mathbb {R}^n)$
is defined as the set of all locally integrable functions f such that
$Q_{\kappa }(\mathbb {R}^n)$
is defined as the set of all locally integrable functions f such that
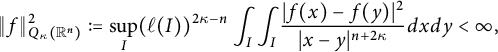 $$ \begin{align*} \|f\|_{Q_{\kappa}(\mathbb{R}^n)}^{2}:=\sup\limits_{I}(\ell(I))^{2\kappa-n}\int_{I}\int_{I} \frac{|f(x)-f(y)|^2}{|x-y|^{n+2\kappa}}dx dy<\infty, \end{align*} $$
$$ \begin{align*} \|f\|_{Q_{\kappa}(\mathbb{R}^n)}^{2}:=\sup\limits_{I}(\ell(I))^{2\kappa-n}\int_{I}\int_{I} \frac{|f(x)-f(y)|^2}{|x-y|^{n+2\kappa}}dx dy<\infty, \end{align*} $$
where the symbol
![]() $\sup _{I}$
denotes the supremum taken over all cubes I with the edge length
$\sup _{I}$
denotes the supremum taken over all cubes I with the edge length
![]() $\ell (I)$
and the edges parallel to the coordinate axes in
$\ell (I)$
and the edges parallel to the coordinate axes in
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
In the literature, Q-type spaces were introduced as a new class of function spaces between
![]() $W^{1,n}(\mathbb {R}^{n})$
and
$W^{1,n}(\mathbb {R}^{n})$
and
![]() $BMO(\mathbb {R}^{n})$
. In 1995, Aulaskari, Xiao, and Zhao [Reference Aulaskari, Xiao and Zhao3] first introduced a class of Möbius invariant analytic function space
$BMO(\mathbb {R}^{n})$
. In 1995, Aulaskari, Xiao, and Zhao [Reference Aulaskari, Xiao and Zhao3] first introduced a class of Möbius invariant analytic function space
![]() $Q_{p}(\mathbb {D})$
for
$Q_{p}(\mathbb {D})$
for
![]() $p\in (0,1)$
on the unit disk
$p\in (0,1)$
on the unit disk
![]() $\mathbb {D}$
of the complex plane. The class
$\mathbb {D}$
of the complex plane. The class
![]() $Q_{p}(\mathbb {D})$
,
$Q_{p}(\mathbb {D})$
,
![]() $p\in (0,1)$
can be seen as subspaces and subsets of
$p\in (0,1)$
can be seen as subspaces and subsets of
![]() $BMOA$
and
$BMOA$
and
![]() $UBC$
on
$UBC$
on
![]() $\mathbb {D}$
and were investigated extensively (see Aulaskari, Stegenga, and Xiao [Reference Aulaskari, Stegenga and Xiao2], Aulaskari, Xiao, and Zhao [Reference Aulaskari, Xiao and Zhao3], Xiao [Reference Xiao37, Reference Xiao40] and the references therein). As a class of analytic function spaces, the boundary of
$\mathbb {D}$
and were investigated extensively (see Aulaskari, Stegenga, and Xiao [Reference Aulaskari, Stegenga and Xiao2], Aulaskari, Xiao, and Zhao [Reference Aulaskari, Xiao and Zhao3], Xiao [Reference Xiao37, Reference Xiao40] and the references therein). As a class of analytic function spaces, the boundary of
![]() $Q_{p}(\mathbb {D})$
is
$Q_{p}(\mathbb {D})$
is
![]() $Q_{p}(\partial \mathbb {D})$
which was introduced by Nicolau and Xiao in [Reference Nicolau and Xiao35], where
$Q_{p}(\partial \mathbb {D})$
which was introduced by Nicolau and Xiao in [Reference Nicolau and Xiao35], where
![]() $\partial \mathbb D$
denotes the boundary of
$\partial \mathbb D$
denotes the boundary of
![]() $\mathbb D$
. Correspondingly, in the setting of Euclidean spaces, the real-variable Q-type spaces
$\mathbb D$
. Correspondingly, in the setting of Euclidean spaces, the real-variable Q-type spaces
![]() $Q_{\kappa }(\mathbb R^{n})$
were first introduced by Essén, Janson, Peng, and Xiao [Reference Essén, Janson, Peng and Xiao16]. Since then, various characterizations of Q-type spaces have been established (see Cui and Yang [Reference Cui and Yang10], Dafni and Xiao [Reference Dafni and Xiao11, Reference Dafni and Xiao12], Yang and Yuan [Reference Yang and Yuan44, Reference Yang and Yuan45] and the references therein).
$Q_{\kappa }(\mathbb R^{n})$
were first introduced by Essén, Janson, Peng, and Xiao [Reference Essén, Janson, Peng and Xiao16]. Since then, various characterizations of Q-type spaces have been established (see Cui and Yang [Reference Cui and Yang10], Dafni and Xiao [Reference Dafni and Xiao11, Reference Dafni and Xiao12], Yang and Yuan [Reference Yang and Yuan44, Reference Yang and Yuan45] and the references therein).
By the aid of Hausdorff capacities and tent spaces, Dafni and Xiao [Reference Dafni and Xiao11] proved the following equivalent characterization of
![]() $Q_{\kappa }(\mathbb R^{n})$
.
$Q_{\kappa }(\mathbb R^{n})$
.
Theorem 5.2 [Reference Dafni and Xiao11, Theorems 3.3 and 7.0]
Given a
![]() $C^{\infty }$
real-valued function
$C^{\infty }$
real-valued function
![]() $\psi $
on
$\psi $
on
![]() $\mathbb R^{n}$
with
$\mathbb R^{n}$
with
Let
![]() $\psi _{t}(x):=t^{-n}\psi (x/t)$
. Then
$\psi _{t}(x):=t^{-n}\psi (x/t)$
. Then
![]() $f\in Q_{v/2}(\mathbb R^{n})$
with
$f\in Q_{v/2}(\mathbb R^{n})$
with
![]() $\nu \in (0,\min \{ 2, n\})$
if and only if
$\nu \in (0,\min \{ 2, n\})$
if and only if
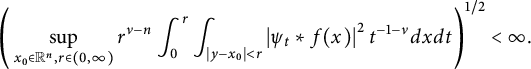 $$ \begin{align*}\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left|\psi_{t}\ast f(x)\right|^{2}t^{-1-\nu}d{x}d{t}\Bigg)^{1/2}<\infty.\end{align*} $$
$$ \begin{align*}\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left|\psi_{t}\ast f(x)\right|^{2}t^{-1-\nu}d{x}d{t}\Bigg)^{1/2}<\infty.\end{align*} $$
Remark 5.3 In [Reference Dafni and Xiao11],
![]() $\psi $
is defined as a function satisfying
$\psi $
is defined as a function satisfying
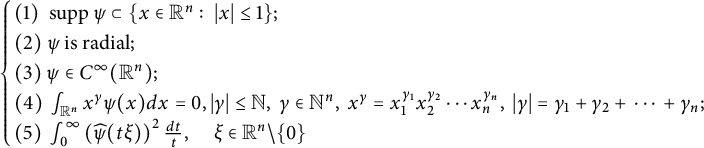 $$ \begin{align*} \begin{cases} &\!\!\!\!\!\!(1)\ \text{ supp }\psi\subset\{x\in\mathbb R^{n}:\ |x|\leq 1\};\\ &\!\!\!\!\!\!(2)\ \psi \text{ is radial};\\ &\!\!\!\!\!\!(3)\ \psi\in C^{\infty}(\mathbb R^{n});\\ &\!\!\!\!\!\!(4)\ \int_{\mathbb R^{n}}x^{\gamma}\psi(x)dx=0, |\gamma|\leq \mathbb N,\ \gamma\in\mathbb{N}^{n},\ x^{\gamma}=x_{1}^{\gamma_{1}}x_{2}^{\gamma_{2}}\cdots x_{n}^{\gamma_{n}},\ |\gamma|=\gamma_{1}+\gamma_{2}+\cdots+\gamma_{n};\\ &\!\!\!\!\!\!(5)\ \int^{\infty}_{0}\left(\widehat{\psi}(t\xi)\right)^{2}\frac{dt}{t},\quad \xi\in\mathbb R^{n}\backslash \{0\}\\ \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} &\!\!\!\!\!\!(1)\ \text{ supp }\psi\subset\{x\in\mathbb R^{n}:\ |x|\leq 1\};\\ &\!\!\!\!\!\!(2)\ \psi \text{ is radial};\\ &\!\!\!\!\!\!(3)\ \psi\in C^{\infty}(\mathbb R^{n});\\ &\!\!\!\!\!\!(4)\ \int_{\mathbb R^{n}}x^{\gamma}\psi(x)dx=0, |\gamma|\leq \mathbb N,\ \gamma\in\mathbb{N}^{n},\ x^{\gamma}=x_{1}^{\gamma_{1}}x_{2}^{\gamma_{2}}\cdots x_{n}^{\gamma_{n}},\ |\gamma|=\gamma_{1}+\gamma_{2}+\cdots+\gamma_{n};\\ &\!\!\!\!\!\!(5)\ \int^{\infty}_{0}\left(\widehat{\psi}(t\xi)\right)^{2}\frac{dt}{t},\quad \xi\in\mathbb R^{n}\backslash \{0\}\\ \end{cases} \end{align*} $$
(see [Reference Dafni and Xiao11, Lemma 3.1]). In fact, Theorem 5.2 also holds for the functions
![]() $\psi $
which satisfy (5.1) (see [Reference Xiao41, p. 228]).
$\psi $
which satisfy (5.1) (see [Reference Xiao41, p. 228]).
As an application of Theorem 5.2, we can obtain the following result.
Theorem 5.4 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $t>0$
,
$t>0$
,
![]() $f\in Q_{\nu /2}(\mathbb R^{n})$
and
$f\in Q_{\nu /2}(\mathbb R^{n})$
and
![]() $\nu \in (0,\min \{ 2, n\})$
. For
$\nu \in (0,\min \{ 2, n\})$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f. There hold the following local Sobolev-type trace inequalities
$u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f. There hold the following local Sobolev-type trace inequalities
 $$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\nonumber \end{align} $$
$$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\nonumber \end{align} $$
and
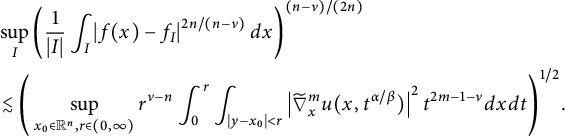 $$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\nonumber \end{align} $$
$$ \begin{align} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\nonumber \end{align} $$
Proof Let
 $$ \begin{align*} \psi_{1,t}(x)=t^{-n}\psi_1(x/t):=t^m\frac{\partial^mG_{t^{\alpha/\beta}}^{\alpha,\beta}(x)}{\partial t^m} \end{align*} $$
$$ \begin{align*} \psi_{1,t}(x)=t^{-n}\psi_1(x/t):=t^m\frac{\partial^mG_{t^{\alpha/\beta}}^{\alpha,\beta}(x)}{\partial t^m} \end{align*} $$
and
![]() $C^i_{\alpha ,\beta ,m}$
is a constant depend on
$C^i_{\alpha ,\beta ,m}$
is a constant depend on
![]() $i,\alpha ,m$
. It can be deduced from the Fourier transform that
$i,\alpha ,m$
. It can be deduced from the Fourier transform that
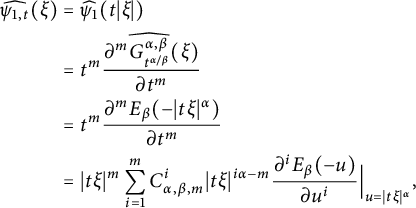 $$ \begin{align*} \widehat{\psi_{1,t}}(\xi)&=\widehat{\psi_{1}}(t|\xi|)\\ &=t^{m}\frac{\partial^{m}\widehat{G^{\alpha,\beta}_{t^{\alpha/\beta}}}(\xi)}{\partial t^{m}}\\ &=t^{m}\frac{\partial^{m}E_{\beta}(-|t\xi|^{\alpha})}{\partial t^{m}}\\ &=|t\xi|^{m}\sum^{m}_{i=1} C^i_{\alpha,\beta,m}|t\xi|^{i\alpha-m}\frac{\partial^{i}E_{\beta}(-u)}{\partial u^{i}}\Big|_{u=|t\xi|^{\alpha}}, \end{align*} $$
$$ \begin{align*} \widehat{\psi_{1,t}}(\xi)&=\widehat{\psi_{1}}(t|\xi|)\\ &=t^{m}\frac{\partial^{m}\widehat{G^{\alpha,\beta}_{t^{\alpha/\beta}}}(\xi)}{\partial t^{m}}\\ &=t^{m}\frac{\partial^{m}E_{\beta}(-|t\xi|^{\alpha})}{\partial t^{m}}\\ &=|t\xi|^{m}\sum^{m}_{i=1} C^i_{\alpha,\beta,m}|t\xi|^{i\alpha-m}\frac{\partial^{i}E_{\beta}(-u)}{\partial u^{i}}\Big|_{u=|t\xi|^{\alpha}}, \end{align*} $$
which implies that
where
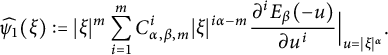 $$ \begin{align} \widehat{\psi_{1}}(\xi):=|\xi|^{m}\sum^{m}_{i=1}C^i_{\alpha,\beta,m}|\xi|^{i\alpha-m}\frac{\partial^{i}E_{\beta}(-u)}{\partial u^{i}}\Big|_{u=|\xi|^{\alpha}}. \end{align} $$
$$ \begin{align} \widehat{\psi_{1}}(\xi):=|\xi|^{m}\sum^{m}_{i=1}C^i_{\alpha,\beta,m}|\xi|^{i\alpha-m}\frac{\partial^{i}E_{\beta}(-u)}{\partial u^{i}}\Big|_{u=|\xi|^{\alpha}}. \end{align} $$
By (5.4), we can get
It follows from Proposition 2.10 that for
![]() $\alpha>n+m,$
$\alpha>n+m,$
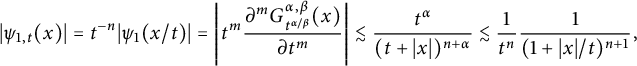 $$ \begin{align*}|\psi_{1,t}(x)|=t^{-n}|\psi_{1}(x/t)|= \left|t^{m}\frac{\partial^mG_{t^{\alpha/\beta}}^{\alpha,\beta}(x)}{\partial t^m}\right| \lesssim \frac{t^{\alpha}}{(t+|x|)^{n+\alpha}} \lesssim \frac{1}{t^{n}}\frac{1}{(1+|x|/t)^{n+1}},\end{align*} $$
$$ \begin{align*}|\psi_{1,t}(x)|=t^{-n}|\psi_{1}(x/t)|= \left|t^{m}\frac{\partial^mG_{t^{\alpha/\beta}}^{\alpha,\beta}(x)}{\partial t^m}\right| \lesssim \frac{t^{\alpha}}{(t+|x|)^{n+\alpha}} \lesssim \frac{1}{t^{n}}\frac{1}{(1+|x|/t)^{n+1}},\end{align*} $$
which gives
![]() $|\psi _{1}(x)|\lesssim (1+|x|)^{-n-1}$
and
$|\psi _{1}(x)|\lesssim (1+|x|)^{-n-1}$
and
![]() $\psi _{1}\in L^{1}(\mathbb R^{n})$
. Then Theorem 5.2 implies
$\psi _{1}\in L^{1}(\mathbb R^{n})$
. Then Theorem 5.2 implies
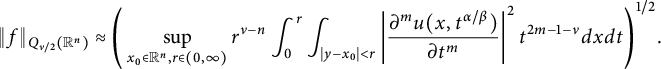 $$ \begin{align*}\|f\|_{Q_{\nu/2}(\mathbb{R}^{n})}\approx\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m}\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\end{align*} $$
$$ \begin{align*}\|f\|_{Q_{\nu/2}(\mathbb{R}^{n})}\approx\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m}\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\end{align*} $$
Since
![]() $Q_{\nu /2}(\mathbb R^{n})$
is a subspace of
$Q_{\nu /2}(\mathbb R^{n})$
is a subspace of
![]() $BMO(\mathbb R^{n})$
, we have
$BMO(\mathbb R^{n})$
, we have
![]() $\|f\|_{BMO(\mathbb {R}^{n})}\leq \|f\|_{Q_{\nu /2}(\mathbb {R}^{n})}$
. We can deduce from the equivalent norm:
$\|f\|_{BMO(\mathbb {R}^{n})}\leq \|f\|_{Q_{\nu /2}(\mathbb {R}^{n})}$
. We can deduce from the equivalent norm:
 $$ \begin{align} \|f\|_{BMO(\mathbb{R}^{n})}&:=&\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|d{x}\right)\simeq \sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)} \end{align} $$
$$ \begin{align} \|f\|_{BMO(\mathbb{R}^{n})}&:=&\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|d{x}\right)\simeq \sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)} \end{align} $$
that
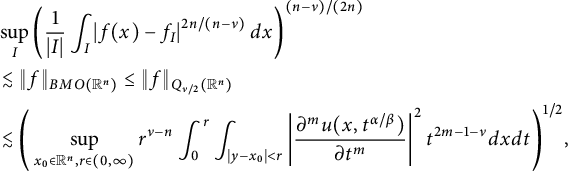 $$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim \|f\|_{BMO(\mathbb R^{n})}\leq\|f\|_{Q_{\nu/2}(\mathbb R^{n})}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}, \end{align*} $$
$$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim \|f\|_{BMO(\mathbb R^{n})}\leq\|f\|_{Q_{\nu/2}(\mathbb R^{n})}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}, \end{align*} $$
which proves (5.2).
Now, we prove (5.3). Denote
It can be deduced from the Fourier transform that
which implies that
where
By (5.6), it is easy to verify that
Also, it follows from Proposition 2.11 that for
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
which gives
![]() $|\psi _{2}(x)|\lesssim (1+|x|)^{-n-1}$
and
$|\psi _{2}(x)|\lesssim (1+|x|)^{-n-1}$
and
![]() $\psi _{2}\in L^{1}(\mathbb R^{n})$
. Theorem 5.2 implies
$\psi _{2}\in L^{1}(\mathbb R^{n})$
. Theorem 5.2 implies
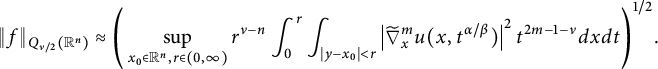 $$ \begin{align*}\|f\|_{Q_{\nu/2}(\mathbb{R}^{n})}\approx\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^mu(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\end{align*} $$
$$ \begin{align*}\|f\|_{Q_{\nu/2}(\mathbb{R}^{n})}\approx\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^mu(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}.\end{align*} $$
Similarly, using (5.5), we have
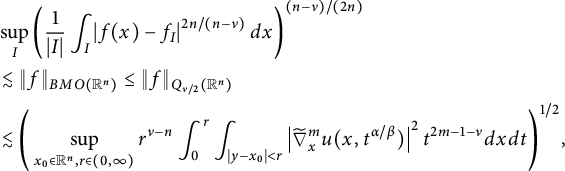 $$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim \|f\|_{BMO(\mathbb R^{n})}\leq\|f\|_{Q_{\nu/2}(\mathbb R^{n})}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}, \end{align*} $$
$$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim \|f\|_{BMO(\mathbb R^{n})}\leq\|f\|_{Q_{\nu/2}(\mathbb R^{n})}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}, \end{align*} $$
which proves (5.3).
Remark 5.5 Let
![]() $m\in \mathbb {Z}_+$
,
$m\in \mathbb {Z}_+$
,
![]() $\alpha>n+m$
,
$\alpha>n+m$
,
![]() $\beta \in (0,1] $
,
$\beta \in (0,1] $
,
![]() $s>0$
,
$s>0$
,
![]() $f\in Q_{\nu /2}(\mathbb R^{n})$
and
$f\in Q_{\nu /2}(\mathbb R^{n})$
and
![]() ${\nu \in (0,\min \{2, n\})}$
. For
${\nu \in (0,\min \{2, n\})}$
. For
![]() $(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
$(x,t)\in \mathbb R^{n}\times (0,\infty )$
, denote by
![]() $u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f. There hold the local Sobolev-type trace inequalities
$u(x,t)=G_{t}^{\alpha ,\beta }*f(x)$
the time-space fractional extension of f. There hold the local Sobolev-type trace inequalities
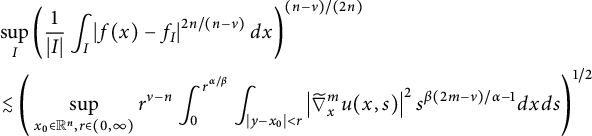 $$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,s)\right| ^2s^{\beta(2m-\nu)/\alpha-1}d{x}d{s}\Bigg)^{1/2}\nonumber \end{align*} $$
$$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,s)\right| ^2s^{\beta(2m-\nu)/\alpha-1}d{x}d{s}\Bigg)^{1/2}\nonumber \end{align*} $$
and
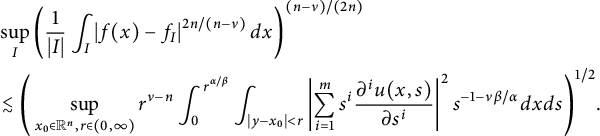 $$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \sum_{i=1}^{m}s^i\frac{\partial^iu(x,s)}{\partial s^i} \right| ^2s^{-1-\nu\beta/\alpha}d{x}d{s}\Bigg)^{1/2}.\nonumber \end{align*} $$
$$ \begin{align*} &\sup_{I}\left(\frac{1}{|I|} \int_{I}\left|f(x)-f_{I}\right|^{2n/(n-\nu)}d{x}\right)^{(n-\nu)/(2n)}\\ &\lesssim\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \sum_{i=1}^{m}s^i\frac{\partial^iu(x,s)}{\partial s^i} \right| ^2s^{-1-\nu\beta/\alpha}d{x}d{s}\Bigg)^{1/2}.\nonumber \end{align*} $$
In fact, by
![]() $s=t^{\alpha /\beta }$
and (3.19), we get
$s=t^{\alpha /\beta }$
and (3.19), we get
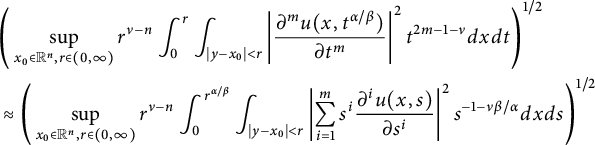 $$ \begin{align*} &\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\\ &\approx\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \sum_{i=1}^{m} s^i\frac{\partial^iu(x,s)}{\partial s^i} \right| ^2s^{-1-\nu\beta/\alpha}d{x}d{s}\Bigg)^{1/2}\nonumber \end{align*} $$
$$ \begin{align*} &\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \frac{\partial^mu(x,t^{\alpha/\beta})}{\partial t^m} \right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\\ &\approx\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \sum_{i=1}^{m} s^i\frac{\partial^iu(x,s)}{\partial s^i} \right| ^2s^{-1-\nu\beta/\alpha}d{x}d{s}\Bigg)^{1/2}\nonumber \end{align*} $$
and
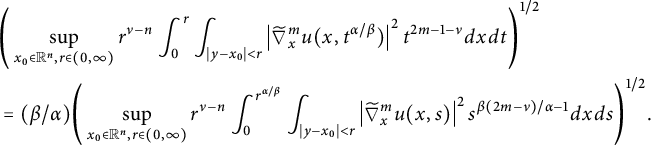 $$ \begin{align*} &\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\\ &=(\beta/\alpha)\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,s)\right| ^2s^{\beta(2m-\nu)/\alpha-1}d{x}d{s}\Bigg)^{1/2}.\nonumber \end{align*} $$
$$ \begin{align*} &\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,t^{\alpha/\beta})\right| ^2t^{2m-1-\nu}d{x}d{t}\Bigg)^{1/2}\\ &=(\beta/\alpha)\Bigg(\sup_{x_{0}\in\mathbb{R}^{n},r\in(0,\infty)}r^{\nu-n}\int^{r^{\alpha/\beta}}_{0}\int_{|y-x_{0}|<r}\left| \widetilde{\nabla}_{x}^m u(x,s)\right| ^2s^{\beta(2m-\nu)/\alpha-1}d{x}d{s}\Bigg)^{1/2}.\nonumber \end{align*} $$