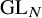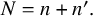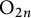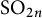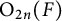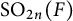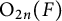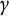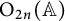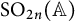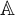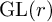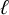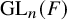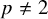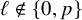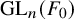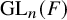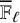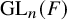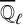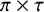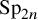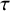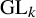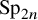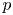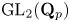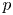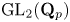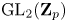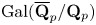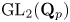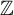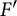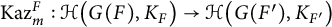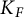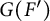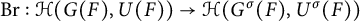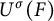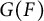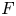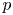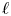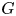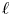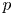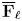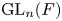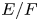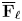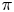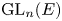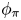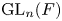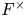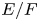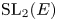Refine search
Actions for selected content:
160 results
The dual pair
 $\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
$\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 October 2025, e174
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DENOMINATORS IN LUSZTIG’S ASYMPTOTIC HECKE ALGEBRA VIA THE PLANCHEREL FORMULA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EISENSTEIN COHOMOLOGY FOR ORTHOGONAL GROUPS AND THE SPECIAL VALUES OF L-FUNCTIONS FOR
 $\mathrm {GL}_1 \times \mathrm {O}(2n)$
$\mathrm {GL}_1 \times \mathrm {O}(2n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 2463-2522
- Print publication:
- November 2025
-
- Article
- Export citation
Eisenstein Cohomology for
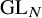 $\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
$\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The global Gan-Gross-Prasad conjecture for unitary groups. II. From Eisenstein series to Bessel periods
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-polynomial representations of double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 April 2025, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The local converse theorem for quasi-split
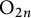 $\mathrm {O}_{2n}$ and
$\mathrm {O}_{2n}$ and 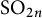 $\mathrm {SO}_{2n}$
$\mathrm {SO}_{2n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-38
-
- Article
- Export citation
SIMPLE TYPE THEORY FOR METAPLECTIC COVERS OF
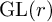 $\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
$\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1263-1335
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arthur packets for pure real forms of symplectic and special orthogonal groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1-22
-
- Article
- Export citation
Cuspidal
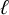 ${\ell }$-modular representations of
${\ell }$-modular representations of 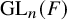 $\operatorname {GL}_n({ F})$ distinguished by a Galois involution
$\operatorname {GL}_n({ F})$ distinguished by a Galois involution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 February 2025, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An Iwahori theoretic mod
 $p$ local Langlands correspondence
$p$ local Langlands correspondence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 805-817
- Print publication:
- September 2025
-
- Article
- Export citation
Doubling constructions and tensor product L-functions: coverings of the symplectic group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local newforms for generic representations of unramified even unitary groups I: Even conductor case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Presentation of an Iwasawa algebra: The pro-p Iwahori of simple, simply connected, split groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 377-394
- Print publication:
- June 2025
-
- Article
- Export citation
Restriction of p-adic representations of GL2(Qp) to parahoric subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 74-119
- Print publication:
- January 2025
-
- Article
- Export citation
A nonabelian Fourier transform for tempered unipotent representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 13-73
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compatibility of Kazhdan and Brauer homomorphism
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 19-43
- Print publication:
- March 2025
-
- Article
- Export citation
On some mod p representations of quaternion algebra over ℚp
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2585-2655
- Print publication:
- November 2024
-
- Article
- Export citation
Modulo ℓ distinction problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 30 September 2024, pp. 2285-2321
- Print publication:
- October 2024
-
- Article
- Export citation
Hyperbolic actions of higher rank lattices come from rank-one factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 961-988
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation