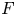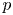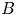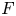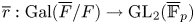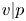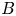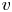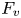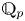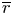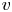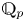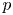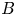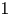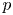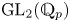1. Introduction
Let ![]() $p$ be a prime number. The mod
$p$ be a prime number. The mod ![]() $p$ (and
$p$ (and ![]() $p$-adic) Langlands program has been emerged starting from the fundamental work of Breuil [Reference BreuilBre03]. Up to present, the correspondence in the case of
$p$-adic) Langlands program has been emerged starting from the fundamental work of Breuil [Reference BreuilBre03]. Up to present, the correspondence in the case of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ has been well-understood in various aspects, by the work of [Reference BreuilBre03, Reference ColmezCol10, Reference EmertonEme11, Reference PaškūnasPaš13]. Recently, there have been significant progress towards a mod
$\mathrm {GL}_2(\mathbb {Q}_p)$ has been well-understood in various aspects, by the work of [Reference BreuilBre03, Reference ColmezCol10, Reference EmertonEme11, Reference PaškūnasPaš13]. Recently, there have been significant progress towards a mod ![]() $p$ Langlands correspondence for
$p$ Langlands correspondence for ![]() $\mathrm {GL}_2(L)$, when
$\mathrm {GL}_2(L)$, when ![]() $L$ is a finite unramified extension of
$L$ is a finite unramified extension of ![]() $\mathbb {Q}_p$ (see [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Reference Hu and WangHW22, Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS21]). However, a mod
$\mathbb {Q}_p$ (see [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Reference Hu and WangHW22, Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS21]). However, a mod ![]() $p$ Jacquet–Langlands correspondence is still largely unknown, even in the case of
$p$ Jacquet–Langlands correspondence is still largely unknown, even in the case of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$.
$\mathrm {GL}_2(\mathbb {Q}_p)$.
Inspired by the local–global compatibility results [Reference EmertonEme11, Reference Buzzard, Diamond and JarvisBDJ10], it is natural to search for the correspondence in the cohomology of Shimura curves. To explain this, let ![]() $F$ be a totally real extension of
$F$ be a totally real extension of ![]() $\mathbb {Q}$ in which
$\mathbb {Q}$ in which ![]() $p$ is unramified. Let
$p$ is unramified. Let ![]() $B$ be a quaternion algebra over
$B$ be a quaternion algebra over ![]() $F$, which we assume to be split at only one infinite place in this introduction (in the text, we will also treat the case where
$F$, which we assume to be split at only one infinite place in this introduction (in the text, we will also treat the case where ![]() $B$ is definite). If
$B$ is definite). If ![]() $U$ is a compact open subgroup of
$U$ is a compact open subgroup of ![]() $(B\otimes _F\mathbb {A}_{F,f})^{\times }$, let
$(B\otimes _F\mathbb {A}_{F,f})^{\times }$, let ![]() $X_U$ be the associated smooth projective Shimura curve over
$X_U$ be the associated smooth projective Shimura curve over ![]() $F$. Let
$F$. Let ![]() $\overline {r}:\operatorname {{\mathrm {Gal}}}(\overline {F}/F)\rightarrow \mathrm {GL}_2(\overline {\mathbb {F}}_p)$ be a continuous absolutely irreducible representation. Fix a place
$\overline {r}:\operatorname {{\mathrm {Gal}}}(\overline {F}/F)\rightarrow \mathrm {GL}_2(\overline {\mathbb {F}}_p)$ be a continuous absolutely irreducible representation. Fix a place ![]() $v$ above
$v$ above ![]() $p$ and a compact open subgroup
$p$ and a compact open subgroup ![]() $U^v\subset (B\otimes _{F}\mathbb {A}_{F,f}^{\{v\}})^{\times }$, where
$U^v\subset (B\otimes _{F}\mathbb {A}_{F,f}^{\{v\}})^{\times }$, where ![]() $\mathbb {A}_{F,f}^{\{v\}}$ denotes the ring of finite adèles of
$\mathbb {A}_{F,f}^{\{v\}}$ denotes the ring of finite adèles of ![]() $F$ outside
$F$ outside ![]() $v$. We define
$v$. We define
where ![]() $U_v$ runs over compact open subgroups of
$U_v$ runs over compact open subgroups of ![]() $B_v^{\times } :=(B\otimes _{F}F_v)^{\times }$. In this way, we obtain an admissible smooth representation of
$B_v^{\times } :=(B\otimes _{F}F_v)^{\times }$. In this way, we obtain an admissible smooth representation of ![]() $B_v^{\times }$. We assume that
$B_v^{\times }$. We assume that ![]() $B$ ramifies at
$B$ ramifies at ![]() $v$ from now on.
$v$ from now on.
Assume that ![]() $\pi _v^B(\overline {r})$ is nonzero, i.e.
$\pi _v^B(\overline {r})$ is nonzero, i.e. ![]() $\overline {r}$ is modular for
$\overline {r}$ is modular for ![]() $B$ and
$B$ and ![]() $U^v$; we also need to impose some extra assumptions on
$U^v$; we also need to impose some extra assumptions on ![]() $\overline {r}$, see § 5 for details. Then it is known that
$\overline {r}$, see § 5 for details. Then it is known that ![]() $\pi ^B_v(\overline {r})$ is infinite-dimensional (cf. [Reference Breuil and DiamondBD14, Corollary 3.5.4] and [Reference ScholzeScho18, Theorem 1.4]). On the other hand, since
$\pi ^B_v(\overline {r})$ is infinite-dimensional (cf. [Reference Breuil and DiamondBD14, Corollary 3.5.4] and [Reference ScholzeScho18, Theorem 1.4]). On the other hand, since ![]() $B_v^{\times }$ is compact modulo its centre, irreducible smooth mod
$B_v^{\times }$ is compact modulo its centre, irreducible smooth mod ![]() $p$ representations of
$p$ representations of ![]() $B_v^{\times }$ (with a fixed central character) are easy to classify. Actually, such a representation always has dimension
$B_v^{\times }$ (with a fixed central character) are easy to classify. Actually, such a representation always has dimension ![]() $\leq 2$ and there are only finitely many isomorphism classes. This implies that
$\leq 2$ and there are only finitely many isomorphism classes. This implies that ![]() $\pi _v^B(\overline {r})$ is necessarily of infinite length, and is built out by infinitely many pieces of a finite number of isomorphism classes of irreducible representations of
$\pi _v^B(\overline {r})$ is necessarily of infinite length, and is built out by infinitely many pieces of a finite number of isomorphism classes of irreducible representations of ![]() $B_v^{\times }$ in a highly non-semisimple way. A natural way to study such a representation is to look at its socle filtration. More conceptually, there is a standard invariant which measures the growth of the dimension of this socle filtration, called Gelfand–Kirillov dimension (cf. § 1.1).
$B_v^{\times }$ in a highly non-semisimple way. A natural way to study such a representation is to look at its socle filtration. More conceptually, there is a standard invariant which measures the growth of the dimension of this socle filtration, called Gelfand–Kirillov dimension (cf. § 1.1).
In this paper, we study the Gelfand–Kirillov dimension of ![]() $\pi _v^B(\overline {r})$ in the case
$\pi _v^B(\overline {r})$ in the case ![]() $F_v\cong \mathbb {Q}_p$. We make this assumption and assume
$F_v\cong \mathbb {Q}_p$. We make this assumption and assume ![]() $p\geq 5$ from now on; the reason for this restriction will be explained below after more notation is introduced.
$p\geq 5$ from now on; the reason for this restriction will be explained below after more notation is introduced.
Let ![]() $\overline {\rho }:=\overline {r}_v(1)$. We make the following assumption on
$\overline {\rho }:=\overline {r}_v(1)$. We make the following assumption on ![]() $\overline {\rho }$.
$\overline {\rho }$.
(H1) Assume that
 $\overline {\rho }$ has one of the following forms:
$\overline {\rho }$ has one of the following forms:•
 $\overline {\rho }$ is absolutely irreducible and up to twist
$\overline {\rho }$ is absolutely irreducible and up to twist  $\overline {\rho }|_{I(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)} \sim \big (\begin{smallmatrix} \omega _{2}^{r+1} & 0 \\ 0 & \omega _2^{p(r+1)} \end{smallmatrix}\big )$, with
$\overline {\rho }|_{I(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)} \sim \big (\begin{smallmatrix} \omega _{2}^{r+1} & 0 \\ 0 & \omega _2^{p(r+1)} \end{smallmatrix}\big )$, with  $2\leq r\leq p-3$, where
$2\leq r\leq p-3$, where  $\omega _2$ is Serre's fundamental character of niveau 2;
$\omega _2$ is Serre's fundamental character of niveau 2;•
 $\overline {\rho }$ is reducible nonsplit and up to twist
$\overline {\rho }$ is reducible nonsplit and up to twist  $\overline {\rho }|_{I(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)} \sim \big (\begin{smallmatrix} \omega ^{r+1} & * \\ 0 & 1 \end{smallmatrix}\big )$, with
$\overline {\rho }|_{I(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)} \sim \big (\begin{smallmatrix} \omega ^{r+1} & * \\ 0 & 1 \end{smallmatrix}\big )$, with  $0\leq r \leq p-3$, where
$0\leq r \leq p-3$, where  $\omega$ is the mod
$\omega$ is the mod  $p$ cyclotomic character of
$p$ cyclotomic character of  $\operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)$.
$\operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)$.
The following is our main result.
Theorem 1.1 Keep the above assumptions on ![]() $F$,
$F$, ![]() $B$ and
$B$ and ![]() $\overline {r}$. Then
$\overline {r}$. Then ![]() $\pi _v^B(\overline {r})$ has Gelfand–Kirillov dimension
$\pi _v^B(\overline {r})$ has Gelfand–Kirillov dimension ![]() $1$.
$1$.
An analogue of Theorem 1.1 was previously proved by Paškūnas [Reference PaškūnasPaš22] when ![]() $\overline {\rho }$ is reducible, using Scholze's functor (introduced in [Reference ScholzeScho18]) and a result of Ludwig [Reference LudwigLud17]. Combining with some argument of [Reference PaškūnasPaš22], Theorem 1.1 implies some vanishing result on Scholze's functor, see Theorem 1.2 below.
$\overline {\rho }$ is reducible, using Scholze's functor (introduced in [Reference ScholzeScho18]) and a result of Ludwig [Reference LudwigLud17]. Combining with some argument of [Reference PaškūnasPaš22], Theorem 1.1 implies some vanishing result on Scholze's functor, see Theorem 1.2 below.
The proof of Theorem 1.1 follows the innovative method of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23] (which treats the case of ![]() $\mathrm {GL}_2$ over an unramified extension of
$\mathrm {GL}_2$ over an unramified extension of ![]() $\mathbb {Q}_{p}$), but has several differences in technique. To explain this, recall that one key step in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23] is to compare some potentially crystalline deformation rings of
$\mathbb {Q}_{p}$), but has several differences in technique. To explain this, recall that one key step in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23] is to compare some potentially crystalline deformation rings of ![]() $\overline {\rho }$ of different (tame) types, and use it to gain information about the first three steps of the socle filtration of certain
$\overline {\rho }$ of different (tame) types, and use it to gain information about the first three steps of the socle filtration of certain ![]() $\overline {\mathbb {F}}_p$-representations of
$\overline {\mathbb {F}}_p$-representations of ![]() $\mathrm {GL}_2$ with respect to the Iwahori subgroup. In [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23], the relevant deformation rings are explicitly worked out by complicated computations, but unfortunately in doing this a stronger genericity condition on
$\mathrm {GL}_2$ with respect to the Iwahori subgroup. In [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23], the relevant deformation rings are explicitly worked out by complicated computations, but unfortunately in doing this a stronger genericity condition on ![]() $\overline {\rho }$ is imposed, for example
$\overline {\rho }$ is imposed, for example ![]() $12\leq r\leq p-15$ when
$12\leq r\leq p-15$ when ![]() $\overline {\rho }$ is reducible. One may wonder, assuming this stronger genericity condition, if (the analogue of) Theorem 1.1 remains true when
$\overline {\rho }$ is reducible. One may wonder, assuming this stronger genericity condition, if (the analogue of) Theorem 1.1 remains true when ![]() $F_v$ is an unramified extension of
$F_v$ is an unramified extension of ![]() $\mathbb {Q}_p$, namely if
$\mathbb {Q}_p$, namely if ![]() $\pi _v^B(\overline {r})$ has Gelfand–Kirillov dimension equal to
$\pi _v^B(\overline {r})$ has Gelfand–Kirillov dimension equal to ![]() $[F_v:\mathbb {Q}_p]$. We believe this should be true and provable using the method of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23]. In fact, we do give a criterion for controlling the Gelfand–Kirillov dimension in this generality, see Corollary 2.12 (which is an analogue of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Corollary 5.3.5]). However, we caution that using only the deformation rings computed in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23] may not be enough to prove this statement, because by the classical Jacquet–Langlands correspondence only those involving discrete series inertial types are useful to obtain information about
$[F_v:\mathbb {Q}_p]$. We believe this should be true and provable using the method of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23]. In fact, we do give a criterion for controlling the Gelfand–Kirillov dimension in this generality, see Corollary 2.12 (which is an analogue of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Corollary 5.3.5]). However, we caution that using only the deformation rings computed in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23] may not be enough to prove this statement, because by the classical Jacquet–Langlands correspondence only those involving discrete series inertial types are useful to obtain information about ![]() $\pi _v^B(\overline {r})$. Namely, to check the condition of Corollary 2.12, one possibly needs to compute extra deformation rings (of discrete series inertial type), even when
$\pi _v^B(\overline {r})$. Namely, to check the condition of Corollary 2.12, one possibly needs to compute extra deformation rings (of discrete series inertial type), even when ![]() $F_v=\mathbb {Q}_p$.
$F_v=\mathbb {Q}_p$.
For the above reason and also with the wish to weaken as much as possible the genericity condition in Theorem 1.1, we have chosen to restrict to the case ![]() $F_v \cong \mathbb {Q}_p$. The point is that in this case there is an alternative construction of Kisin's potentially semistable deformation rings, due to Paškūnas [Reference PaškūnasPaš15]. This construction works only for two-dimensional representations of
$F_v \cong \mathbb {Q}_p$. The point is that in this case there is an alternative construction of Kisin's potentially semistable deformation rings, due to Paškūnas [Reference PaškūnasPaš15]. This construction works only for two-dimensional representations of ![]() $\operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)$ and, in general, does not allow us to determine the explicit form of these rings, but it fits perfectly with our aim for the following two reasons.
$\operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)$ and, in general, does not allow us to determine the explicit form of these rings, but it fits perfectly with our aim for the following two reasons.
– First, to carry out the strategy in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23], we do not really need the explicit form of these deformation rings, but only certain congruence relations between them (cf. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Proposition 4.3.3]). In Paškūnas’ construction, these congruence relations can be proved by congruence relations between suitably chosen integral lattices inside the corresponding types.
– Second, this construction closely relates the structure of the deformation rings to the structure of
 $\pi (\overline {\rho })$, the admissible smooth representation of
$\pi (\overline {\rho })$, the admissible smooth representation of  $\mathrm {GL}_2(\mathbb {Q}_p)$ associated to
$\mathrm {GL}_2(\mathbb {Q}_p)$ associated to  $\overline {\rho }$ by the mod
$\overline {\rho }$ by the mod  $p$ local Langlands correspondence (see § 4.2 for the precise definition). Thus, we may make use of the results of [Reference Barthel and LivnéBL94, Reference BreuilBre03, Reference MorraMor11, Reference MorraMor17] on
$p$ local Langlands correspondence (see § 4.2 for the precise definition). Thus, we may make use of the results of [Reference Barthel and LivnéBL94, Reference BreuilBre03, Reference MorraMor11, Reference MorraMor17] on  $\pi (\overline {\rho })$ to study these deformation rings; see Theorem 4.15 for such an example.
$\pi (\overline {\rho })$ to study these deformation rings; see Theorem 4.15 for such an example.
In addition, in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23] they use potentially crystalline deformation rings of Hodge–Tate weights ![]() $(-1,2)$ (and of
$(-1,2)$ (and of ![]() $(0,1)$), while we use deformation rings of Hodge–Tate weights
$(0,1)$), while we use deformation rings of Hodge–Tate weights ![]() $(0,2)$. This also allows a further (minor) improvement on the genericity condition.
$(0,2)$. This also allows a further (minor) improvement on the genericity condition.
Theorem 1.1 can be applied to study Scholze's functors. Let ![]() $L$ be a finite extension of
$L$ be a finite extension of ![]() $\mathbb {Q}_p$ (not necessarily unramified). Let
$\mathbb {Q}_p$ (not necessarily unramified). Let ![]() $D$ be the central division algebra over
$D$ be the central division algebra over ![]() $L$ of dimension
$L$ of dimension ![]() $n^2$ and invariant
$n^2$ and invariant ![]() $1/n$, Scholze [Reference ScholzeScho18] has constructed a cohomological covariant
$1/n$, Scholze [Reference ScholzeScho18] has constructed a cohomological covariant ![]() $\delta$-functor
$\delta$-functor ![]() $\{\mathcal {S}^i, i\geq 0\}$ from the category of admissible smooth representations of
$\{\mathcal {S}^i, i\geq 0\}$ from the category of admissible smooth representations of ![]() $\mathrm {GL}_n(L)$ over
$\mathrm {GL}_n(L)$ over ![]() $\overline {\mathbb {F}}_p$ to admissible smooth representations of
$\overline {\mathbb {F}}_p$ to admissible smooth representations of ![]() $D^{\times }$ which carry a continuous and commuting action of
$D^{\times }$ which carry a continuous and commuting action of ![]() $\operatorname {{\mathrm {Gal}}}(\overline {L}/L)$. If
$\operatorname {{\mathrm {Gal}}}(\overline {L}/L)$. If ![]() $\pi$ is an admissible smooth representation of
$\pi$ is an admissible smooth representation of ![]() $\mathrm {GL}_n(L)$ over
$\mathrm {GL}_n(L)$ over ![]() $\overline {\mathbb {F}}_p$, then
$\overline {\mathbb {F}}_p$, then ![]() $\mathcal {S}^i(\pi )$ is defined as the cohomology group
$\mathcal {S}^i(\pi )$ is defined as the cohomology group ![]() $H^i_{\mathrm {\acute {e}t}}(\mathbb {P}_{\mathbb {C}_p}^{n-1},\mathcal {F}_{\pi })$, where
$H^i_{\mathrm {\acute {e}t}}(\mathbb {P}_{\mathbb {C}_p}^{n-1},\mathcal {F}_{\pi })$, where ![]() $\mathcal {F}_{\pi }$ is a certain Weil-equivariant sheaf on the adic space
$\mathcal {F}_{\pi }$ is a certain Weil-equivariant sheaf on the adic space ![]() $\mathbb {P}_{\mathbb {C}_p}^{n-1}$. His construction is expected to realize both
$\mathbb {P}_{\mathbb {C}_p}^{n-1}$. His construction is expected to realize both ![]() $p$-adic local Langlands and Jacquet–Langlands correspondences. In general, these cohomology groups seem very difficult to compute, but Scholze has computed
$p$-adic local Langlands and Jacquet–Langlands correspondences. In general, these cohomology groups seem very difficult to compute, but Scholze has computed ![]() $\mathcal {S}^0(\pi )$ and showed that
$\mathcal {S}^0(\pi )$ and showed that ![]() $\mathcal {S}^i(\pi )$ vanishes whenever
$\mathcal {S}^i(\pi )$ vanishes whenever ![]() $i>2(n-1)$. Specializing to
$i>2(n-1)$. Specializing to ![]() $n=2$, the case we are interested in, we have
$n=2$, the case we are interested in, we have ![]() $\mathcal {S}^i(-)=0$ for
$\mathcal {S}^i(-)=0$ for ![]() $i>2$. Later on, Ludwig proved that
$i>2$. Later on, Ludwig proved that ![]() $\mathcal {S}^2(\pi )=0$ if either
$\mathcal {S}^2(\pi )=0$ if either ![]() $\pi$ is principal series or special series of
$\pi$ is principal series or special series of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$, using the geometry of perfectoid modular curves [Reference LudwigLud17]. Since it is easy to compute
$\mathrm {GL}_2(\mathbb {Q}_p)$, using the geometry of perfectoid modular curves [Reference LudwigLud17]. Since it is easy to compute ![]() $\mathcal {S}^2(\pi )$ if
$\mathcal {S}^2(\pi )$ if ![]() $\pi$ is one-dimensional, this leaves only the case of supersingular representations for
$\pi$ is one-dimensional, this leaves only the case of supersingular representations for ![]() $\mathcal {S}^2$.
$\mathcal {S}^2$.
By Breuil's classification [Reference BreuilBre03], any supersingular representation of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ with a central character is up to twist isomorphic to
$\mathrm {GL}_2(\mathbb {Q}_p)$ with a central character is up to twist isomorphic to
where ![]() $0\leq r\leq p-1$ and
$0\leq r\leq p-1$ and ![]() $T$ is a certain Hecke operator [Reference Barthel and LivnéBL94]. As an application of Theorem 1.1, we have the following result.
$T$ is a certain Hecke operator [Reference Barthel and LivnéBL94]. As an application of Theorem 1.1, we have the following result.
Theorem 1.2 Let ![]() $\pi$ be a supersingular representation of
$\pi$ be a supersingular representation of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ as above and assume
$\mathrm {GL}_2(\mathbb {Q}_p)$ as above and assume ![]() $2\leq r\leq p-3$. Then
$2\leq r\leq p-3$. Then ![]() $\mathcal {S}^2(\pi )=0$.
$\mathcal {S}^2(\pi )=0$.
Our proof of Theorem 1.2 is inspired by Paškūnas’ work [Reference PaškūnasPaš22], where he has used Ludwig's vanishing result of ![]() $\mathcal {S}^2$ to prove Theorem 1.1 in the case
$\mathcal {S}^2$ to prove Theorem 1.1 in the case ![]() $\overline {\rho }$ is reducible. We observe that his argument can actually go in reverse direction, namely the vanishing of
$\overline {\rho }$ is reducible. We observe that his argument can actually go in reverse direction, namely the vanishing of ![]() $\mathcal {S}^2$ on supersingular
$\mathcal {S}^2$ on supersingular ![]() $\pi$ can be deduced from the Gelfand–Kirillov dimension of
$\pi$ can be deduced from the Gelfand–Kirillov dimension of ![]() $\mathcal {S}^1(\pi )$ (see Proposition 7.4). Thus, Theorem 1.2 follows from Theorem 1.1 and a local–global compatibility result à la Emerton [Reference EmertonEme11, Reference Dospinescu and Le BrasDLB17].
$\mathcal {S}^1(\pi )$ (see Proposition 7.4). Thus, Theorem 1.2 follows from Theorem 1.1 and a local–global compatibility result à la Emerton [Reference EmertonEme11, Reference Dospinescu and Le BrasDLB17].
Another reason for focusing on the case of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ is that we can prove some finer results on the structure of
$\mathrm {GL}_2(\mathbb {Q}_p)$ is that we can prove some finer results on the structure of ![]() $\mathcal {S}^1(\pi (\overline {\rho }))$. We put
$\mathcal {S}^1(\pi (\overline {\rho }))$. We put
 \[
\mathrm{JL}(\overline{\rho})=\left\{\begin{array}{@{}lll}
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\chi\omega^{-1},\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{if}\ \overline{\rho}\sim \bigg(\begin{matrix}
{\chi} & {*}\\ {0} & {\chi\omega}\end{matrix}\bigg), \\
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\overline{\rho}\otimes\omega^{-1},\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{otherwise}. \end{array}\right. \]
\[
\mathrm{JL}(\overline{\rho})=\left\{\begin{array}{@{}lll}
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\chi\omega^{-1},\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{if}\ \overline{\rho}\sim \bigg(\begin{matrix}
{\chi} & {*}\\ {0} & {\chi\omega}\end{matrix}\bigg), \\
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\overline{\rho}\otimes\omega^{-1},\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{otherwise}. \end{array}\right. \]
Theorem 1.3 Let ![]() $\overline {\rho }$ be as in (H1).
$\overline {\rho }$ be as in (H1).
(i) Assume
 $\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$ for any character
$\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$ for any character  $\chi$. Then
$\chi$. Then  $\mathcal {S}^1(\pi (\overline {\rho }))\cong (\overline {\rho }\otimes \omega ^{-1})\otimes \mathrm {JL}(\overline {\rho })$ as representations of
$\mathcal {S}^1(\pi (\overline {\rho }))\cong (\overline {\rho }\otimes \omega ^{-1})\otimes \mathrm {JL}(\overline {\rho })$ as representations of  $\operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)\times B_v^{\times }$.
$\operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p/\mathbb {Q}_p)\times B_v^{\times }$.(ii) Assume
 $\overline {\rho }$ is reducible. Denote by
$\overline {\rho }$ is reducible. Denote by  $\overline {\rho }^{\rm ss}$ the semisimplification of
$\overline {\rho }^{\rm ss}$ the semisimplification of  $\overline {\rho }$.
$\overline {\rho }$.
(a) Assume
 $\overline {\rho }^{\rm ss}\nsim \chi \oplus \chi \omega$ for any
$\overline {\rho }^{\rm ss}\nsim \chi \oplus \chi \omega$ for any  $\chi$. Then
$\chi$. Then  $\mathrm {JL}(\overline {\rho })$ depends only on
$\mathrm {JL}(\overline {\rho })$ depends only on  $\overline {\rho }^{\rm ss}$.
$\overline {\rho }^{\rm ss}$.(b) Let
 $\overline {\rho }_1\sim \big (\begin{smallmatrix} {\omega } & {*}\\ {0} & {1}\end{smallmatrix}\big )$ and
$\overline {\rho }_1\sim \big (\begin{smallmatrix} {\omega } & {*}\\ {0} & {1}\end{smallmatrix}\big )$ and  $\overline {\rho }_2\sim \big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$ be nonsplit extensions. Then there exists an admissible
$\overline {\rho }_2\sim \big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$ be nonsplit extensions. Then there exists an admissible  $\overline {\mathbb {F}}_p$-representation
$\overline {\mathbb {F}}_p$-representation  $V$ of
$V$ of  $B_v^{\times }$ such that
$B_v^{\times }$ such that
 \begin{gather*} 0\rightarrow
\mathbf{1}_{D^{\times}}\rightarrow
\mathrm{JL}(\overline{\rho}_1)\rightarrow V\rightarrow0,\\
0\rightarrow V\rightarrow
\mathrm{JL}(\overline{\rho}_2)\rightarrow
(\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow 0.
\end{gather*}
\begin{gather*} 0\rightarrow
\mathbf{1}_{D^{\times}}\rightarrow
\mathrm{JL}(\overline{\rho}_1)\rightarrow V\rightarrow0,\\
0\rightarrow V\rightarrow
\mathrm{JL}(\overline{\rho}_2)\rightarrow
(\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow 0.
\end{gather*}
It may look surprising that the representation ![]() $\mathrm {JL}(\overline {\rho })$ does not determine
$\mathrm {JL}(\overline {\rho })$ does not determine ![]() $\overline {\rho }$, but only
$\overline {\rho }$, but only ![]() $\overline {\rho }^{\rm ss}$, in case (a) of Theorem 1.3(ii); see Remark 8.13 for an explanation. It would be interesting to describe the precise structure of
$\overline {\rho }^{\rm ss}$, in case (a) of Theorem 1.3(ii); see Remark 8.13 for an explanation. It would be interesting to describe the precise structure of ![]() $\mathrm {JL}(\overline {\rho })$. We plan to come back to this question in future work.
$\mathrm {JL}(\overline {\rho })$. We plan to come back to this question in future work.
We now give a brief overview of the contents of each section. In § 2, we study the structure of the ![]() $p$-adic group
$p$-adic group ![]() $B_v^{\times }$ and prove a criterion for controlling the Gelfand–Kirillov dimension of its representations (analogous to [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 5]). In § 3 we study the structure of integral lattices in various locally algebraic types of
$B_v^{\times }$ and prove a criterion for controlling the Gelfand–Kirillov dimension of its representations (analogous to [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 5]). In § 3 we study the structure of integral lattices in various locally algebraic types of ![]() $\mathrm {GL}_2(\mathbb {Z}_p)$. In § 4, we use Paškūnas’ technique to study potentially crystalline deformation rings of tame type and Hodge–Tate weights
$\mathrm {GL}_2(\mathbb {Z}_p)$. In § 4, we use Paškūnas’ technique to study potentially crystalline deformation rings of tame type and Hodge–Tate weights ![]() $(0,2)$. In §§ 5 and 6, we carry out the gluing process for
$(0,2)$. In §§ 5 and 6, we carry out the gluing process for ![]() $B_v^{\times }$-representations and prove our main result, Theorem 1.1. Finally, we study Scholze's functors, and prove Theorem 1.2 in § 7 and Theorem 1.3 in § 8.
$B_v^{\times }$-representations and prove our main result, Theorem 1.1. Finally, we study Scholze's functors, and prove Theorem 1.2 in § 7 and Theorem 1.3 in § 8.
1.1 Notation
We fix a prime number ![]() $p\geq 5$. Let
$p\geq 5$. Let ![]() $E\subset \overline {\mathbb {Q}}_p$ be a finite unramified extension of
$E\subset \overline {\mathbb {Q}}_p$ be a finite unramified extension of ![]() $\mathbb {Q}_p$, with ring of integers
$\mathbb {Q}_p$, with ring of integers ![]() $\mathcal {O}$ and residue field
$\mathcal {O}$ and residue field ![]() $\mathbb {F}$. We will assume without further comment that
$\mathbb {F}$. We will assume without further comment that ![]() $\mathbb {F}$ is sufficiently large.
$\mathbb {F}$ is sufficiently large.
If ![]() $F$ is a field, let
$F$ is a field, let ![]() $G_F := \operatorname {{\mathrm {Gal}}}({\overline {F}}/F)$ denote its absolute Galois group. Let
$G_F := \operatorname {{\mathrm {Gal}}}({\overline {F}}/F)$ denote its absolute Galois group. Let ![]() $\varepsilon$ denote the
$\varepsilon$ denote the ![]() $p$-adic cyclotomic character of
$p$-adic cyclotomic character of ![]() $G_F$, and
$G_F$, and ![]() $\omega$ the mod
$\omega$ the mod ![]() $p$ cyclotomic character.
$p$ cyclotomic character.
If ![]() $F$ is a
$F$ is a ![]() $p$-adic field,
$p$-adic field, ![]() $V$ is a de Rham
$V$ is a de Rham ![]() $p$-adic representation of
$p$-adic representation of ![]() $G_F$ over
$G_F$ over ![]() $E$, and
$E$, and ![]() $\kappa : F\hookrightarrow E$, then we will write
$\kappa : F\hookrightarrow E$, then we will write ![]() ${\rm HT}_{\kappa } (V)$ for the multiset of Hodge–Tate weights of
${\rm HT}_{\kappa } (V)$ for the multiset of Hodge–Tate weights of ![]() $V$ with respect to
$V$ with respect to ![]() $\kappa$. By definition,
$\kappa$. By definition, ![]() ${\rm HT}_{\kappa } (V)$ consists of
${\rm HT}_{\kappa } (V)$ consists of ![]() $- i$ with multiplicity
$- i$ with multiplicity ![]() $\dim _E(V \otimes _{\kappa, F} \widehat {{\overline {F}}}(i))^{G_F}$, e.g.
$\dim _E(V \otimes _{\kappa, F} \widehat {{\overline {F}}}(i))^{G_F}$, e.g. ![]() ${\rm HT}_{\kappa } (\varepsilon ) = \{1\}$ at all embedding
${\rm HT}_{\kappa } (\varepsilon ) = \{1\}$ at all embedding ![]() $\kappa$.
$\kappa$.
If ![]() $G$ is a
$G$ is a ![]() $p$-adic analytic group, we denote by
$p$-adic analytic group, we denote by ![]() $\operatorname {\mathrm {Mod}}_G^{\rm sm}(\mathcal {O})$ the category of smooth representations of
$\operatorname {\mathrm {Mod}}_G^{\rm sm}(\mathcal {O})$ the category of smooth representations of ![]() $G$ on
$G$ on ![]() $\mathcal {O}$-torsion modules. Let
$\mathcal {O}$-torsion modules. Let ![]() $\operatorname {\mathrm {Mod}}_G^{\rm l.adm}(\mathcal {O})$ (respectively,
$\operatorname {\mathrm {Mod}}_G^{\rm l.adm}(\mathcal {O})$ (respectively, ![]() $\operatorname {\mathrm {Mod}}_G^{\rm adm}(\mathcal {O})$) denote the full subcategory of locally admissible (respectively, admissible) representations. If
$\operatorname {\mathrm {Mod}}_G^{\rm adm}(\mathcal {O})$) denote the full subcategory of locally admissible (respectively, admissible) representations. If ![]() $\zeta : Z_G \to \mathcal {O}^{\times }$ is a continuous character of the centre of
$\zeta : Z_G \to \mathcal {O}^{\times }$ is a continuous character of the centre of ![]() $G$, then we denote by
$G$, then we denote by ![]() $\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm sm}(\mathcal {O})$ (respectively,
$\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm sm}(\mathcal {O})$ (respectively, ![]() $\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm l.adm}(\mathcal {O})$, respectively,
$\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm l.adm}(\mathcal {O})$, respectively, ![]() $\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm adm}(\mathcal {O})$) the full subcategory of
$\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm adm}(\mathcal {O})$) the full subcategory of ![]() $\operatorname {\mathrm {Mod}}_G^{\rm sm}(\mathcal {O})$ consisting of smooth (respectively, locally admissible, respectively, admissible) representations on which
$\operatorname {\mathrm {Mod}}_G^{\rm sm}(\mathcal {O})$ consisting of smooth (respectively, locally admissible, respectively, admissible) representations on which ![]() $Z_G$ acts by the character
$Z_G$ acts by the character ![]() $\zeta$.
$\zeta$.
The Pontryagin duality ![]() $M \mapsto M^{\vee }: = \operatorname {{\mathrm {Hom}}}_{\mathcal {O}}^{\rm cont}(M , E/\mathcal {O})$ induces an anti-equivalence between the category of discrete
$M \mapsto M^{\vee }: = \operatorname {{\mathrm {Hom}}}_{\mathcal {O}}^{\rm cont}(M , E/\mathcal {O})$ induces an anti-equivalence between the category of discrete ![]() $\mathcal {O}$-modules and the category of pseudo-compact
$\mathcal {O}$-modules and the category of pseudo-compact ![]() $\mathcal {O}$-modules. Under this duality the category
$\mathcal {O}$-modules. Under this duality the category ![]() $\operatorname {\mathrm {Mod}}_G^{\rm sm}(\mathcal {O})$ is anti-equivalent to the category of profinite augmented
$\operatorname {\mathrm {Mod}}_G^{\rm sm}(\mathcal {O})$ is anti-equivalent to the category of profinite augmented ![]() $G$-representations over
$G$-representations over ![]() $\mathcal {O}$ which is denoted by
$\mathcal {O}$ which is denoted by ![]() $\operatorname {\mathrm {Mod}}_G^{\rm pro}(\mathcal {O})$. Let
$\operatorname {\mathrm {Mod}}_G^{\rm pro}(\mathcal {O})$. Let ![]() $\frak {C}_{G}(\mathcal {O})$ (respectively,
$\frak {C}_{G}(\mathcal {O})$ (respectively, ![]() $\frak {C}_{G,\zeta }(\mathcal {O})$) denote the full subcategory of
$\frak {C}_{G,\zeta }(\mathcal {O})$) denote the full subcategory of ![]() $\operatorname {\mathrm {Mod}}_G^{\rm pro}(\mathcal {O})$ which is anti-equivalent to
$\operatorname {\mathrm {Mod}}_G^{\rm pro}(\mathcal {O})$ which is anti-equivalent to ![]() $\operatorname {\mathrm {Mod}}_{G}^{\rm l.adm}(\mathcal {O})$ (respectively,
$\operatorname {\mathrm {Mod}}_{G}^{\rm l.adm}(\mathcal {O})$ (respectively, ![]() $\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm l.adm}(\mathcal {O})$) under the Pontryagin duality. Note that on an object in
$\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm l.adm}(\mathcal {O})$) under the Pontryagin duality. Note that on an object in ![]() $\frak {C}_{G,\zeta }(\mathcal {O})$ the centre is acting by
$\frak {C}_{G,\zeta }(\mathcal {O})$ the centre is acting by ![]() $\zeta ^{-1}$.
$\zeta ^{-1}$.
Let ![]() $(R,\mathfrak {m})$ be a complete noetherian local commutative
$(R,\mathfrak {m})$ be a complete noetherian local commutative ![]() $\mathcal {O}$-algebra with residue field
$\mathcal {O}$-algebra with residue field ![]() $\mathbb {F}$. We define the category
$\mathbb {F}$. We define the category ![]() $\operatorname {\mathrm {Mod}}_{G}^{\rm sm}(R)$ of smooth
$\operatorname {\mathrm {Mod}}_{G}^{\rm sm}(R)$ of smooth ![]() $R[G]$-modules, and the category
$R[G]$-modules, and the category ![]() $\operatorname {\mathrm {Mod}}_{G}^{\rm l.adm}(R)$ of locally admissible smooth
$\operatorname {\mathrm {Mod}}_{G}^{\rm l.adm}(R)$ of locally admissible smooth ![]() $R[G]$-modules as in [Reference PaškūnasPaš13, § 2]. Let
$R[G]$-modules as in [Reference PaškūnasPaš13, § 2]. Let ![]() $\frak {C}_{G}(R)$ be the dual category of
$\frak {C}_{G}(R)$ be the dual category of ![]() $\operatorname {\mathrm {Mod}}_{G}^{\rm l.adm}(R)$ under the Pontryagin duality. If
$\operatorname {\mathrm {Mod}}_{G}^{\rm l.adm}(R)$ under the Pontryagin duality. If ![]() $\zeta : Z_G \to \mathcal {O}^{\times }$ is a continuous character of the centre of
$\zeta : Z_G \to \mathcal {O}^{\times }$ is a continuous character of the centre of ![]() $G$, we can similarly define
$G$, we can similarly define ![]() $\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm l.adm}(R)$ and its dual category
$\operatorname {\mathrm {Mod}}_{G,\zeta }^{\rm l.adm}(R)$ and its dual category ![]() $\frak {C}_{G,\zeta }(R)$.
$\frak {C}_{G,\zeta }(R)$.
If ![]() $M$ is a torsion-free linear-topological
$M$ is a torsion-free linear-topological ![]() $\mathcal {O}$-module,
$\mathcal {O}$-module, ![]() $M^{d}$ denotes its Schikhof dual
$M^{d}$ denotes its Schikhof dual ![]() $\operatorname {{\mathrm {Hom}}}^{\rm cont}_{\mathcal {O}} (M, \mathcal {O})$. The functor
$\operatorname {{\mathrm {Hom}}}^{\rm cont}_{\mathcal {O}} (M, \mathcal {O})$. The functor ![]() $M \mapsto M^d$ induces an anti-equivalence of categories between the category of pseudo-compact torsion-free linear-topological
$M \mapsto M^d$ induces an anti-equivalence of categories between the category of pseudo-compact torsion-free linear-topological ![]() $\mathcal {O}$-modules and the category of
$\mathcal {O}$-modules and the category of ![]() $\varpi$-adically complete and separated torsion-free
$\varpi$-adically complete and separated torsion-free ![]() $\mathcal {O}$-modules.
$\mathcal {O}$-modules.
If ![]() $R$ is a ring and
$R$ is a ring and ![]() $M$ is a left
$M$ is a left ![]() $R$-module, we denote by
$R$-module, we denote by ![]() $\operatorname {{\mathrm {soc}}}_R(M)$ (respectively,
$\operatorname {{\mathrm {soc}}}_R(M)$ (respectively, ![]() $\mathrm {cosoc}_R(M)$) the socle (respectively, cosocle) of
$\mathrm {cosoc}_R(M)$) the socle (respectively, cosocle) of ![]() $M$. Inductively, we define the socle (respectively, cosocle) filtration of
$M$. Inductively, we define the socle (respectively, cosocle) filtration of ![]() $M$. If
$M$. If ![]() $M$ has finite length, we denote by
$M$ has finite length, we denote by ![]() $\operatorname {{\mathrm {JH}}}(M)$ the set of Jordan–Hölder factors of
$\operatorname {{\mathrm {JH}}}(M)$ the set of Jordan–Hölder factors of ![]() $M$.
$M$.
The grade ![]() $j_{R}(M)$ of
$j_{R}(M)$ of ![]() $M$ over
$M$ over ![]() $R$ is defined by
$R$ is defined by
Assume ![]() $R$ is noetherian. The ring
$R$ is noetherian. The ring ![]() $R$ is called Auslander–Gorenstein if it has finite left and right injective dimension and the following Auslander condition holds: for any
$R$ is called Auslander–Gorenstein if it has finite left and right injective dimension and the following Auslander condition holds: for any ![]() $R$-module
$R$-module ![]() $M$, any integer
$M$, any integer ![]() $m\geq 0$ and any
$m\geq 0$ and any ![]() $R$-submodule
$R$-submodule ![]() $N$ of
$N$ of ![]() $\operatorname {{\mathrm {Ext}}}^m_R(M,R)$, we have
$\operatorname {{\mathrm {Ext}}}^m_R(M,R)$, we have ![]() $j_{R}(N)\geq m$. An Auslander–Gorenstein ring is called Auslander regular if it has finite global dimension. If
$j_{R}(N)\geq m$. An Auslander–Gorenstein ring is called Auslander regular if it has finite global dimension. If ![]() $R$ is an Auslander regular ring and
$R$ is an Auslander regular ring and ![]() $M$ is a finitely generated
$M$ is a finitely generated ![]() $R$-module, define the dimension
$R$-module, define the dimension
where ![]() ${\rm gld}(R)$ is the global dimension of
${\rm gld}(R)$ is the global dimension of ![]() $R$.
$R$.
Let ![]() $G_0$ be a compact
$G_0$ be a compact ![]() $p$-adic analytic group. The ring-theoretic properties of
$p$-adic analytic group. The ring-theoretic properties of ![]() $\mathcal {O} [\![G_0]\!]$ are established by the fundamental works of Lazard [Reference LazardLaz65] and Venjakob [Reference VenjakobVen02]. In particular, if
$\mathcal {O} [\![G_0]\!]$ are established by the fundamental works of Lazard [Reference LazardLaz65] and Venjakob [Reference VenjakobVen02]. In particular, if ![]() $G_0$ has no element of order
$G_0$ has no element of order ![]() $p$, then
$p$, then ![]() $\mathcal {O} [\![G_0]\!]$ is an Auslander regular ring of dimension
$\mathcal {O} [\![G_0]\!]$ is an Auslander regular ring of dimension ![]() $1+\dim _{\mathbb {Q}_p} G_0$, where
$1+\dim _{\mathbb {Q}_p} G_0$, where ![]() $\dim _{\mathbb {Q}_p} G_0$ is the dimension of
$\dim _{\mathbb {Q}_p} G_0$ is the dimension of ![]() $G_0$ as a
$G_0$ as a ![]() $p$-adic analytic group. If
$p$-adic analytic group. If ![]() $M$ is nonzero, we have
$M$ is nonzero, we have
and ![]() $\delta _{ \mathcal {O} [\![G_0]\!]}( M) = 1+\dim _{\mathbb {Q}_p} G_0 - j_{ \mathcal {O} [\![G_0]\!]}(M)$. If
$\delta _{ \mathcal {O} [\![G_0]\!]}( M) = 1+\dim _{\mathbb {Q}_p} G_0 - j_{ \mathcal {O} [\![G_0]\!]}(M)$. If ![]() $G$ is a
$G$ is a ![]() $p$-adic analytic group with a fixed open compact subgroup
$p$-adic analytic group with a fixed open compact subgroup ![]() $G_0 \subseteq G$ and
$G_0 \subseteq G$ and ![]() $M$ is a finitely generated
$M$ is a finitely generated ![]() $\mathcal {O} [\![G_0]\!]$-module equipped with a compatible
$\mathcal {O} [\![G_0]\!]$-module equipped with a compatible ![]() $G$-action, we define
$G$-action, we define ![]() $j_{G}(M)$ (respectively,
$j_{G}(M)$ (respectively, ![]() $\delta _G(M)$) as
$\delta _G(M)$) as ![]() $j_{\mathcal {O}[\![G_0]\!]}(M)$ (respectively,
$j_{\mathcal {O}[\![G_0]\!]}(M)$ (respectively, ![]() $\delta _{\mathcal {O}[\![G_0]\!]}(M)$); this does not depend on the choice of
$\delta _{\mathcal {O}[\![G_0]\!]}(M)$); this does not depend on the choice of ![]() $G_0$.
$G_0$.
If ![]() $\pi$ is an admissible smooth representation of
$\pi$ is an admissible smooth representation of ![]() $G$ over
$G$ over ![]() $\mathbb {F}$, then
$\mathbb {F}$, then ![]() $\pi ^{\vee }$ is finitely generated over
$\pi ^{\vee }$ is finitely generated over ![]() $\mathcal {O} [\![G_0]\!]$. The Gelfand–Kirillov dimension of
$\mathcal {O} [\![G_0]\!]$. The Gelfand–Kirillov dimension of ![]() $\pi$ is defined by (see [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Remark 5.1.1])
$\pi$ is defined by (see [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Remark 5.1.1])
2. The  $p$-adic Lie group
$p$-adic Lie group  $D^{\times }$
$D^{\times }$
2.1 Results of Kohlhaase
We recall and extend some results of [Reference KohlhaaseKoh13].
Let ![]() $L = \mathbb {Q}_{p^f}$ be the unramified extension of degree
$L = \mathbb {Q}_{p^f}$ be the unramified extension of degree ![]() $f$ over
$f$ over ![]() $\mathbb {Q}_p$. Let
$\mathbb {Q}_p$. Let ![]() $D$ be the unique central division algebra of dimension
$D$ be the unique central division algebra of dimension ![]() $4$ over
$4$ over ![]() $L$. For
$L$. For ![]() $a\in D$, define
$a\in D$, define ![]() $v_D(a) := v_p ({\rm Nrd}_D(a))$, where
$v_D(a) := v_p ({\rm Nrd}_D(a))$, where ![]() $v_p$ is the
$v_p$ is the ![]() $p$-adic valuation on
$p$-adic valuation on ![]() $L$ normalized so that
$L$ normalized so that ![]() $v_p(p) = 1$, and
$v_p(p) = 1$, and ![]() ${\rm Nrd}_D : D \to L$ is the reduced norm map; this gives a non-archimedean valuation on
${\rm Nrd}_D : D \to L$ is the reduced norm map; this gives a non-archimedean valuation on ![]() $D$. Let
$D$. Let ![]() ${\mathcal {O}}_D : =\{a\in D\,|\, v_D(a) \geq 0\}$ be the ring of integers and
${\mathcal {O}}_D : =\{a\in D\,|\, v_D(a) \geq 0\}$ be the ring of integers and ![]() $\frak {p}_D: = \{a\in D\,|\, v_D(a) \geq 1\}$ the maximal ideal, which can be generated by a uniformizer
$\frak {p}_D: = \{a\in D\,|\, v_D(a) \geq 1\}$ the maximal ideal, which can be generated by a uniformizer ![]() $\varpi _D$. The residue field
$\varpi _D$. The residue field ![]() $k_D : = {\mathcal {O}}_D/\frak {p}_D$ is isomorphic to
$k_D : = {\mathcal {O}}_D/\frak {p}_D$ is isomorphic to ![]() $\mathbb {F}_{q^2}$, where
$\mathbb {F}_{q^2}$, where ![]() $q:= p^f$. Let
$q:= p^f$. Let ![]() $L'$ be the unramified quadratic extension of
$L'$ be the unramified quadratic extension of ![]() $L$ in
$L$ in ![]() $\overline {\mathbb {Q}}_p$. We denote by
$\overline {\mathbb {Q}}_p$. We denote by ![]() $\sigma : L' \to L'$ a lift of the Frobenius map
$\sigma : L' \to L'$ a lift of the Frobenius map ![]() $x \mapsto x^q$ on
$x \mapsto x^q$ on ![]() $\mathbb {F}_{q^2}$. Let
$\mathbb {F}_{q^2}$. Let ![]() $L'\langle X \rangle$ denote the non-commutative polynomial ring in one variable over
$L'\langle X \rangle$ denote the non-commutative polynomial ring in one variable over ![]() $L'$ satisfying the relation
$L'$ satisfying the relation ![]() $X a = \sigma (a) X,~ \forall a \in L'$. Then the homomorphism
$X a = \sigma (a) X,~ \forall a \in L'$. Then the homomorphism ![]() $L'\langle X \rangle \to D$,
$L'\langle X \rangle \to D$, ![]() $X\mapsto \varpi _D$ induces an isomorphism of
$X\mapsto \varpi _D$ induces an isomorphism of ![]() $L$-algebras
$L$-algebras
Let ![]() $D^{\times }$ (respectively,
$D^{\times }$ (respectively, ![]() $\mathcal {O}_D^{\times }$) denote the group of invertible elements of
$\mathcal {O}_D^{\times }$) denote the group of invertible elements of ![]() $D$ (respectively,
$D$ (respectively, ![]() $\mathcal {O}_D$) and
$\mathcal {O}_D$) and
which are compact open normal (pro-![]() $p$) subgroups of
$p$) subgroups of ![]() $D^{\times }$. We have
$D^{\times }$. We have
Let ![]() $Z_D$ denote the centre of
$Z_D$ denote the centre of ![]() $D^{\times }$ which is isomorphic to
$D^{\times }$ which is isomorphic to ![]() $L^{\times }$. Then
$L^{\times }$. Then ![]() $Z_D{\mathcal {O}}_D^{\times }$ is of index
$Z_D{\mathcal {O}}_D^{\times }$ is of index ![]() $2$ in
$2$ in ![]() $D^{\times }$. Let
$D^{\times }$. Let ![]() $Z^1_D = Z_D \cap U^1_D$.
$Z^1_D = Z_D \cap U^1_D$.
Assume ![]() $p \geq 5$. Let
$p \geq 5$. Let ![]() $\omega : U^1_D \backslash \{1\} \to (0, \infty )$ be the map defined by
$\omega : U^1_D \backslash \{1\} \to (0, \infty )$ be the map defined by ![]() $\omega (g) : = \frac {1}{2} v_D (g - 1)$, and set
$\omega (g) : = \frac {1}{2} v_D (g - 1)$, and set ![]() $\omega (1):=\infty$. As in [Reference SchneiderSchn11, Example 23.2], one shows that
$\omega (1):=\infty$. As in [Reference SchneiderSchn11, Example 23.2], one shows that ![]() $\omega$ is a
$\omega$ is a ![]() $p$-valuation on
$p$-valuation on ![]() $U^1_D$ in the sense of Lazard [Reference LazardLaz65, III.2.1.2]. For any real number
$U^1_D$ in the sense of Lazard [Reference LazardLaz65, III.2.1.2]. For any real number ![]() $\nu > 0$, let
$\nu > 0$, let
We set
It is easy to see that ![]() $U_D^i=(U^1_D)_{{i}/{2}}$ and
$U_D^i=(U^1_D)_{{i}/{2}}$ and ![]() $U^{i+1}_D = (U^1_D)_{ ({i}/{2}) +},$ so we have
$U^{i+1}_D = (U^1_D)_{ ({i}/{2}) +},$ so we have
We say a nonzero homogeneous element ![]() $t\in \operatorname {{\mathrm {gr}}} U^1_D$ is of degree
$t\in \operatorname {{\mathrm {gr}}} U^1_D$ is of degree ![]() $i$ if
$i$ if ![]() $t \in U^i_D/ U^{i+1}_D$.
$t \in U^i_D/ U^{i+1}_D$.
As explained in [Reference SchneiderSchn11, § 25], ![]() $\operatorname {{\mathrm {gr}}} U^1_D$ is a graded Lie algebra over the polynomial ring
$\operatorname {{\mathrm {gr}}} U^1_D$ is a graded Lie algebra over the polynomial ring ![]() $\mathbb {F}_p[\varepsilon ]$ by setting
$\mathbb {F}_p[\varepsilon ]$ by setting
and
Note that ![]() $U^i_D/ U^{i+1}_D \cong (\mathbb {F}_{q^2}, + )$ is an
$U^i_D/ U^{i+1}_D \cong (\mathbb {F}_{q^2}, + )$ is an ![]() $\mathbb {F}_q$-vector space by setting
$\mathbb {F}_q$-vector space by setting
where ![]() $[\lambda ] \in \mathcal {O}_L$ is the Teichmüller lift of
$[\lambda ] \in \mathcal {O}_L$ is the Teichmüller lift of ![]() $\lambda \in \mathbb {F}_q$. One checks that the Lie bracket on
$\lambda \in \mathbb {F}_q$. One checks that the Lie bracket on ![]() $\operatorname {{\mathrm {gr}}} U^1_D$ is
$\operatorname {{\mathrm {gr}}} U^1_D$ is ![]() $\mathbb {F}_q$-bilinear, hence
$\mathbb {F}_q$-bilinear, hence ![]() $\operatorname {{\mathrm {gr}}} U^1_D$ becomes a graded Lie algebra over the polynomial ring
$\operatorname {{\mathrm {gr}}} U^1_D$ becomes a graded Lie algebra over the polynomial ring ![]() $\mathbb {F}_q[\varepsilon ]$.
$\mathbb {F}_q[\varepsilon ]$.
Proposition 2.1 The natural map ![]() $\mathbb {F}_q[\varepsilon ] \otimes _{\mathbb {F}_q} (U^1_D/U^2_D \oplus U^2_D / U^3_D) \to \operatorname {{\mathrm {gr}}} U^1_D$ is an isomorphism of
$\mathbb {F}_q[\varepsilon ] \otimes _{\mathbb {F}_q} (U^1_D/U^2_D \oplus U^2_D / U^3_D) \to \operatorname {{\mathrm {gr}}} U^1_D$ is an isomorphism of ![]() $\mathbb {F}_q[\varepsilon ]$-modules.
$\mathbb {F}_q[\varepsilon ]$-modules.
Proof. The proof of [Reference KohlhaaseKoh13, Lemma 3.12] (when ![]() $L=\mathbb {Q}_p$) extends to the general case.
$L=\mathbb {Q}_p$) extends to the general case.
Let ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D} : = \operatorname {{\mathrm {gr}}} U^1_D \otimes _{\mathbb {F}_q[\varepsilon ]} \mathbb {F}_q$ where the map
$\overline {\operatorname {{\mathrm {gr}}} U^1_D} : = \operatorname {{\mathrm {gr}}} U^1_D \otimes _{\mathbb {F}_q[\varepsilon ]} \mathbb {F}_q$ where the map ![]() $\mathbb {F}_q[\varepsilon ] \to \mathbb {F}_q$ sends
$\mathbb {F}_q[\varepsilon ] \to \mathbb {F}_q$ sends ![]() $\varepsilon$ to
$\varepsilon$ to ![]() $0$. We first determine the Lie algebra structure of
$0$. We first determine the Lie algebra structure of ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D}$. Fix
$\overline {\operatorname {{\mathrm {gr}}} U^1_D}$. Fix ![]() $\xi \in \mathbb {F}_{q^2} \setminus \mathbb {F}_q$ and set
$\xi \in \mathbb {F}_{q^2} \setminus \mathbb {F}_q$ and set
where ![]() $[\xi ] \in \mathcal {O}_{L'}$ is the Teichmüller lift of
$[\xi ] \in \mathcal {O}_{L'}$ is the Teichmüller lift of ![]() $\xi$. We have
$\xi$. We have ![]() $\omega (\gamma _{1}) = \omega (\gamma _{2}) = 1/2$ and
$\omega (\gamma _{1}) = \omega (\gamma _{2}) = 1/2$ and ![]() $\omega (\gamma _{3} ) = \omega (\gamma _{4}) = 1$.Footnote 1 Let
$\omega (\gamma _{3} ) = \omega (\gamma _{4}) = 1$.Footnote 1 Let ![]() $\overline {\gamma }_{1},\overline {\gamma }_{2}\in U^1_D/ U^2_D$ be the images of
$\overline {\gamma }_{1},\overline {\gamma }_{2}\in U^1_D/ U^2_D$ be the images of ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$ and let
$\gamma _2$ and let ![]() $\overline {\gamma }_{3},\overline {\gamma }_{4}\in U^2_D/ U^3_D$ be the images of
$\overline {\gamma }_{3},\overline {\gamma }_{4}\in U^2_D/ U^3_D$ be the images of ![]() $\gamma _3$ and
$\gamma _3$ and ![]() $\gamma _4$. Then
$\gamma _4$. Then ![]() $\overline {\gamma }_{1}$,
$\overline {\gamma }_{1}$, ![]() $\overline {\gamma }_{2}$,
$\overline {\gamma }_{2}$, ![]() $\overline {\gamma }_{3}$,
$\overline {\gamma }_{3}$, ![]() $\overline {\gamma }_{4}$ form an
$\overline {\gamma }_{4}$ form an ![]() $\mathbb {F}_q$-basis of
$\mathbb {F}_q$-basis of ![]() $U_D^1/U_D^2\oplus U_D^2/U_D^3$, hence also an
$U_D^1/U_D^2\oplus U_D^2/U_D^3$, hence also an ![]() $\mathbb {F}_q$-basis of
$\mathbb {F}_q$-basis of ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D}$. They satisfy (in
$\overline {\operatorname {{\mathrm {gr}}} U^1_D}$. They satisfy (in ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D}$, i.e. after modulo
$\overline {\operatorname {{\mathrm {gr}}} U^1_D}$, i.e. after modulo ![]() $\varepsilon$)
$\varepsilon$)
see the discussion after [Reference KohlhaaseKoh13, Remark 3.15].
Passing to the quotient group ![]() $U^1_D /Z^1_D$, we can consider
$U^1_D /Z^1_D$, we can consider ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z^1_D} : = \operatorname {{\mathrm {gr}}} U^1_D/Z^1_D \otimes _{\mathbb {F}_q[\varepsilon ]} \mathbb {F}_q$, with the induced filtration on
$\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z^1_D} : = \operatorname {{\mathrm {gr}}} U^1_D/Z^1_D \otimes _{\mathbb {F}_q[\varepsilon ]} \mathbb {F}_q$, with the induced filtration on ![]() $U^1_D/Z^1_D$. Then
$U^1_D/Z^1_D$. Then ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z^1_D}$ is isomorphic to
$\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z^1_D}$ is isomorphic to ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D}/ (\overline {\gamma }_{4} )$ as graded Lie algebras over
$\overline {\operatorname {{\mathrm {gr}}} U^1_D}/ (\overline {\gamma }_{4} )$ as graded Lie algebras over ![]() $\mathbb {F}_q$, where
$\mathbb {F}_q$, where ![]() $(\overline {\gamma }_{4}) : = \mathbb {F}_q \overline {\gamma }_4$ is the sub-Lie algebra of
$(\overline {\gamma }_{4}) : = \mathbb {F}_q \overline {\gamma }_4$ is the sub-Lie algebra of ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D}$ generated by
$\overline {\operatorname {{\mathrm {gr}}} U^1_D}$ generated by ![]() $\overline {\gamma }_{4}$.
$\overline {\gamma }_{4}$.
Let ![]() $\frak {g}_{\mathbb {F}_p} = \mathbb {F}_p e \oplus \mathbb {F}_p f \oplus \mathbb {F}_p h$ be the graded Lie algebra of dimension
$\frak {g}_{\mathbb {F}_p} = \mathbb {F}_p e \oplus \mathbb {F}_p f \oplus \mathbb {F}_p h$ be the graded Lie algebra of dimension ![]() $3$ over
$3$ over ![]() $\mathbb {F}_p$, with
$\mathbb {F}_p$, with ![]() $e$ and
$e$ and ![]() $f$ in degree
$f$ in degree ![]() $1$,
$1$, ![]() $h$ in degree
$h$ in degree ![]() $2$ and satisfying the relations
$2$ and satisfying the relations
From (2.3) we easily deduce the following result.
Corollary 2.2 The graded Lie algebra ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z_D^1}$ is isomorphic to
$\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z_D^1}$ is isomorphic to ![]() $\frak {g}_{\mathbb {F}_q} : =\mathbb {F}_q \otimes _{\mathbb {F}_p} \frak {g}_{\mathbb {F}_p}$.
$\frak {g}_{\mathbb {F}_q} : =\mathbb {F}_q \otimes _{\mathbb {F}_p} \frak {g}_{\mathbb {F}_p}$.
Remark 2.3 One can also deduce the structure of the Lie algebra ![]() $\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z^1_D} \cong \overline {\operatorname {{\mathrm {gr}}} U^1_D}/ (\overline {\gamma }_{4} )$ from the results of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 5.3] by comparing with the pro-
$\overline {\operatorname {{\mathrm {gr}}} U^1_D/Z^1_D} \cong \overline {\operatorname {{\mathrm {gr}}} U^1_D}/ (\overline {\gamma }_{4} )$ from the results of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 5.3] by comparing with the pro-![]() $p$-Iwahori subgroup of
$p$-Iwahori subgroup of ![]() $\mathrm {GL}_2$ over
$\mathrm {GL}_2$ over ![]() $\mathcal {O}_{L'}$.
$\mathcal {O}_{L'}$.
2.2 The graded group algebra
Let ![]() $\mathbb {Z}_p[\![ U^1_D ]\!]=\varprojlim _{i\geq 1}\mathbb {Z}_p[U_D^1/U_D^i]$ be the Iwasawa algebra of
$\mathbb {Z}_p[\![ U^1_D ]\!]=\varprojlim _{i\geq 1}\mathbb {Z}_p[U_D^1/U_D^i]$ be the Iwasawa algebra of ![]() $U^1_D$ over
$U^1_D$ over ![]() $\mathbb {Z}_p$. It is a pseudo-compact local
$\mathbb {Z}_p$. It is a pseudo-compact local ![]() $\mathbb {Z}_p$-algebra. For
$\mathbb {Z}_p$-algebra. For ![]() $\nu \geq 0$, let
$\nu \geq 0$, let ![]() $J_{\nu }$ denote the smallest closed
$J_{\nu }$ denote the smallest closed ![]() $\mathbb {Z}_p$-submodule of
$\mathbb {Z}_p$-submodule of ![]() $\mathbb {Z}_p[\![ U^1_D]\!]$ which contains all elements of the form
$\mathbb {Z}_p[\![ U^1_D]\!]$ which contains all elements of the form ![]() $p^{\ell } (h_1 - 1)\cdots (h_s - 1)$ with
$p^{\ell } (h_1 - 1)\cdots (h_s - 1)$ with ![]() $\ell, s \geq 0$,
$\ell, s \geq 0$, ![]() $h_1,\ldots, h_s \in U^1_D$ and
$h_1,\ldots, h_s \in U^1_D$ and
Let ![]() $J_{\nu +} : = \bigcup _{\nu ' > \nu } J_{\nu '}$. Let
$J_{\nu +} : = \bigcup _{\nu ' > \nu } J_{\nu '}$. Let
which is an associative graded algebra over ![]() $\operatorname {{\mathrm {gr}}} \mathbb {Z}_p := \bigoplus _{i\geq 0} p^i \mathbb {Z}_p/p^{i+1} \mathbb {Z}_p$. It naturally has a graded Lie algebra structure.
$\operatorname {{\mathrm {gr}}} \mathbb {Z}_p := \bigoplus _{i\geq 0} p^i \mathbb {Z}_p/p^{i+1} \mathbb {Z}_p$. It naturally has a graded Lie algebra structure.
The homomorphism of abelian groups ![]() $\mathcal {L}_{\nu } : \operatorname {{\mathrm {gr}}}_{\nu } U^1_D \to J_{\nu } / J_{\nu +}$,
$\mathcal {L}_{\nu } : \operatorname {{\mathrm {gr}}}_{\nu } U^1_D \to J_{\nu } / J_{\nu +}$, ![]() $g (U^1_D)_{\nu + } \mapsto (g-1) + J_{\nu +}$ extends to a homomorphism of graded
$g (U^1_D)_{\nu + } \mapsto (g-1) + J_{\nu +}$ extends to a homomorphism of graded ![]() $\mathbb {F}_p[\varepsilon ]$-Lie algebras
$\mathbb {F}_p[\varepsilon ]$-Lie algebras ![]() $\mathcal {L} : \operatorname {{\mathrm {gr}}} U^1_D \to \operatorname {{\mathrm {gr}}} \mathbb {Z}_p[\![ U^1_D ]\! ]$, where the
$\mathcal {L} : \operatorname {{\mathrm {gr}}} U^1_D \to \operatorname {{\mathrm {gr}}} \mathbb {Z}_p[\![ U^1_D ]\! ]$, where the ![]() $\mathbb {F}_p[\varepsilon ]$-algebra structure on
$\mathbb {F}_p[\varepsilon ]$-algebra structure on ![]() $\operatorname {{\mathrm {gr}}}\mathbb {Z}_p[\![U_D^1]\!]$ is given through the isomorphism
$\operatorname {{\mathrm {gr}}}\mathbb {Z}_p[\![U_D^1]\!]$ is given through the isomorphism ![]() $\mathbb {F}_p[\varepsilon ] \xrightarrow {\sim } \operatorname {{\mathrm {gr}}} \mathbb {Z}_p$,
$\mathbb {F}_p[\varepsilon ] \xrightarrow {\sim } \operatorname {{\mathrm {gr}}} \mathbb {Z}_p$, ![]() $\varepsilon \mapsto p+ p^2 \mathbb {Z}_p \in \operatorname {{\mathrm {gr}}}^1 \mathbb {Z}_p$. Let
$\varepsilon \mapsto p+ p^2 \mathbb {Z}_p \in \operatorname {{\mathrm {gr}}}^1 \mathbb {Z}_p$. Let ![]() $U_{\mathbb {F}_p[\varepsilon ]}(\operatorname {{\mathrm {gr}}} U^1_D)$ be the universal enveloping algebra of
$U_{\mathbb {F}_p[\varepsilon ]}(\operatorname {{\mathrm {gr}}} U^1_D)$ be the universal enveloping algebra of ![]() $\operatorname {{\mathrm {gr}}} U^1_D$ over
$\operatorname {{\mathrm {gr}}} U^1_D$ over ![]() $\mathbb {F}_p[\varepsilon ]$. By the universal property of
$\mathbb {F}_p[\varepsilon ]$. By the universal property of ![]() $U_{\mathbb {F}_p[\varepsilon ]}(\operatorname {{\mathrm {gr}}} U_D^1)$, we have a homomorphism of associative
$U_{\mathbb {F}_p[\varepsilon ]}(\operatorname {{\mathrm {gr}}} U_D^1)$, we have a homomorphism of associative ![]() $\operatorname {{\mathrm {gr}}} \mathbb {Z}_p$-algebras
$\operatorname {{\mathrm {gr}}} \mathbb {Z}_p$-algebras
By [Reference SchneiderSchn11, Theorem 28.3], ![]() $\widetilde {\mathcal {L}}$ is an isomorphism.
$\widetilde {\mathcal {L}}$ is an isomorphism.
In practice, we will consider the Iwasawa algebra associated to the quotient group ![]() $U_D^1/Z_D^1$. Let
$U_D^1/Z_D^1$. Let ![]() $\mathbb {Z}_p[\![U_D^1/Z_D^1]\!]$ (respectively,
$\mathbb {Z}_p[\![U_D^1/Z_D^1]\!]$ (respectively, ![]() $\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$) be the Iwasawa algebra of
$\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$) be the Iwasawa algebra of ![]() $U_D^1/Z_D^1$ over
$U_D^1/Z_D^1$ over ![]() $\mathbb {Z}_p$ (over
$\mathbb {Z}_p$ (over ![]() $\mathbb {F}_p$). We have
$\mathbb {F}_p$). We have ![]() $\mathbb {F}_p[\![U_D^1/Z_D^1]\!]=\mathbb {Z}_p[\![U_D^1/Z_D^1]\!]\otimes _{\mathbb {Z}_p}\mathbb {F}_p$. The filtration
$\mathbb {F}_p[\![U_D^1/Z_D^1]\!]=\mathbb {Z}_p[\![U_D^1/Z_D^1]\!]\otimes _{\mathbb {Z}_p}\mathbb {F}_p$. The filtration ![]() $\{J_{\nu }, \nu \geq 0\}$ induces a filtration on
$\{J_{\nu }, \nu \geq 0\}$ induces a filtration on ![]() $\mathbb {Z}_p[\![U_D^1/Z_D^1]\!]$ and on
$\mathbb {Z}_p[\![U_D^1/Z_D^1]\!]$ and on ![]() $\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$. On the other hand, letting
$\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$. On the other hand, letting ![]() $\frak {m}_{D}$ denote the maximal ideal of
$\frak {m}_{D}$ denote the maximal ideal of ![]() $\mathbb {F}_p[\![ U^1_D/Z^1_D ]\!]$, we may consider the
$\mathbb {F}_p[\![ U^1_D/Z^1_D ]\!]$, we may consider the ![]() $\mathfrak {m}_{D}$-adic filtration on
$\mathfrak {m}_{D}$-adic filtration on ![]() $\mathbb {F}_p[\![ U^1_D/Z^1_D ]\!]$. The following result shows that these two filtrations coincide up to rescaling indices.
$\mathbb {F}_p[\![ U^1_D/Z^1_D ]\!]$. The following result shows that these two filtrations coincide up to rescaling indices.
Lemma 2.4 Denote by ![]() $\overline {J}_{\nu }$ the image of
$\overline {J}_{\nu }$ the image of ![]() $J_{\nu }$ in
$J_{\nu }$ in ![]() $\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$. Then
$\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$. Then ![]() $\overline {J}_{i/2}=\mathfrak {m}_{D}^i$ for any
$\overline {J}_{i/2}=\mathfrak {m}_{D}^i$ for any ![]() $i\geq 0$.
$i\geq 0$.
Proof. The proof of [Reference KohlhaaseKoh13, Lemma 3.13] (when ![]() $L=\mathbb {Q}_p$) extends to the general case.
$L=\mathbb {Q}_p$) extends to the general case.
One checks that ![]() $J_{\nu }\neq J_{\nu +}$ exactly when
$J_{\nu }\neq J_{\nu +}$ exactly when ![]() $\nu = {i}/{2}$ for some
$\nu = {i}/{2}$ for some ![]() $i\geq 0$. Thus, by Lemma 2.4 the graded algebra
$i\geq 0$. Thus, by Lemma 2.4 the graded algebra
is identical to ![]() $\bigoplus _{\nu \geq 0}\overline {J}_{\nu }/\overline {J}_{\nu +}$.
$\bigoplus _{\nu \geq 0}\overline {J}_{\nu }/\overline {J}_{\nu +}$.
Proposition 2.5 There is an isomorphism of graded ![]() $\mathbb {F}_p$-algebras
$\mathbb {F}_p$-algebras
Let ![]() $\mathbb {F}$ be a finite extension of
$\mathbb {F}$ be a finite extension of ![]() $\mathbb {F}_p$ such that
$\mathbb {F}_p$ such that ![]() $\mathbb {F}_q$ embeds into
$\mathbb {F}_q$ embeds into ![]() $\mathbb {F}$. Let
$\mathbb {F}$. Let ![]() $\mathcal {J}$ denote the set of embeddings
$\mathcal {J}$ denote the set of embeddings ![]() $\mathbb {F}_{q} \hookrightarrow \mathbb {F}$ and fix
$\mathbb {F}_{q} \hookrightarrow \mathbb {F}$ and fix ![]() $\sigma _0\in \mathcal {J}$. We label the embeddings
$\sigma _0\in \mathcal {J}$. We label the embeddings ![]() $\sigma _j = \sigma _0 \circ \varphi ^j$, so that
$\sigma _j = \sigma _0 \circ \varphi ^j$, so that ![]() $\mathcal {J}$ is identified with
$\mathcal {J}$ is identified with ![]() $\{0,\ldots, f-1\}$. Let
$\{0,\ldots, f-1\}$. Let ![]() $\frak {g}_j: = \mathbb {F} \otimes _{\mathbb {F}_{q}, \sigma _j} \frak {g}_{\mathbb {F}_{q}}$. We then have
$\frak {g}_j: = \mathbb {F} \otimes _{\mathbb {F}_{q}, \sigma _j} \frak {g}_{\mathbb {F}_{q}}$. We then have ![]() $\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_{q}} = \bigoplus _{j=0}^{f-1} \frak {g}_j$. Let
$\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_{q}} = \bigoplus _{j=0}^{f-1} \frak {g}_j$. Let ![]() $e_j,f_j,h_j \in \frak {g}_j$ denote
$e_j,f_j,h_j \in \frak {g}_j$ denote ![]() $1\otimes e$,
$1\otimes e$, ![]() $1\otimes f$,
$1\otimes f$, ![]() $1\otimes h \in \mathbb {F} \otimes _{\mathbb {F}_{q}, \sigma _j} \frak {g}_{\mathbb {F}_{q}}$.
$1\otimes h \in \mathbb {F} \otimes _{\mathbb {F}_{q}, \sigma _j} \frak {g}_{\mathbb {F}_{q}}$.
We again denote by ![]() $\frak {m}_{D}$ the maximal ideal of
$\frak {m}_{D}$ the maximal ideal of ![]() $\mathbb {F}[\![ U^1_D/Z^1_D ]\!]=\mathbb {F}\otimes _{\mathbb {F}_p}\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$. Then Proposition 2.5 implies that
$\mathbb {F}[\![ U^1_D/Z^1_D ]\!]=\mathbb {F}\otimes _{\mathbb {F}_p}\mathbb {F}_p[\![U_D^1/Z_D^1]\!]$. Then Proposition 2.5 implies that
 \begin{equation} \operatorname{{\mathrm{gr}}}_{\mathfrak{m}_D} \mathbb{F}[\![ U^1_D /Z^1_D ]\!] =\mathbb{F}\otimes_{\mathbb{F}_p} (\operatorname{{\mathrm{gr}}}_{\mathfrak{m}_D} \mathbb{F}_p[\![ U^1_D /Z^1_D ]\! ] ) \cong U_{\mathbb{F}}(\mathbb{F}\otimes_{\mathbb{F}_p} \frak{g}_{\mathbb{F}_q})\cong \bigotimes_{j=0}^{f-1} U_{\mathbb{F}} (\frak{g}_j). \end{equation}
\begin{equation} \operatorname{{\mathrm{gr}}}_{\mathfrak{m}_D} \mathbb{F}[\![ U^1_D /Z^1_D ]\!] =\mathbb{F}\otimes_{\mathbb{F}_p} (\operatorname{{\mathrm{gr}}}_{\mathfrak{m}_D} \mathbb{F}_p[\![ U^1_D /Z^1_D ]\! ] ) \cong U_{\mathbb{F}}(\mathbb{F}\otimes_{\mathbb{F}_p} \frak{g}_{\mathbb{F}_q})\cong \bigotimes_{j=0}^{f-1} U_{\mathbb{F}} (\frak{g}_j). \end{equation}
In particular, we have ![]() $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}^1 \mathbb {F}[\![ U^1_D /Z^1_D ]\!]=\bigoplus _{j=0}^{f-1}(\mathbb {F} e_j\oplus \mathbb {F} f_j)$.
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}^1 \mathbb {F}[\![ U^1_D /Z^1_D ]\!]=\bigoplus _{j=0}^{f-1}(\mathbb {F} e_j\oplus \mathbb {F} f_j)$.
(i) The graded ring
 $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$ is Auslander regular.
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$ is Auslander regular.(ii) The sequence
 $(h_0,\ldots, h_{f-1})$ is a regular sequence of central elements of
$(h_0,\ldots, h_{f-1})$ is a regular sequence of central elements of  $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$. The quotient
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$. The quotient  $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]/(h_0,\ldots, h_{f-1})$ is commutative and is isomorphic to the polynomial ring
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]/(h_0,\ldots, h_{f-1})$ is commutative and is isomorphic to the polynomial ring  $\mathbb {F} [e_j,f_j;\ 0\leq j \leq f-1]$.
$\mathbb {F} [e_j,f_j;\ 0\leq j \leq f-1]$.
Proof. The proof is the same as that of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Theorem 5.3.4].
Theorem 2.6 is not enough for the application to Gelfand–Kirillov dimension, namely Corollary 2.12 below. We shall find eigenbases of ![]() $\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_q}$ for the
$\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_q}$ for the ![]() $\mathbb {F}_{q^2}^{\times }$-action in the next subsection.
$\mathbb {F}_{q^2}^{\times }$-action in the next subsection.
2.3 Gelfand–Kirillov dimension
We regard ![]() $\mathbb {F}_{q^2}^{\times }$ as a subgroup of
$\mathbb {F}_{q^2}^{\times }$ as a subgroup of ![]() $\mathcal {O}_{L'}^{\times }$ via the Teichmüller lifting map, and then as a subgroup of
$\mathcal {O}_{L'}^{\times }$ via the Teichmüller lifting map, and then as a subgroup of ![]() $\mathcal {O}_D^{\times }$ via the fixed embedding
$\mathcal {O}_D^{\times }$ via the fixed embedding ![]() $L'\hookrightarrow D$. It normalizes
$L'\hookrightarrow D$. It normalizes ![]() $U_D^1$, thus acts on
$U_D^1$, thus acts on ![]() $\overline {\operatorname {{\mathrm {gr}}} U_D^1}$ and on
$\overline {\operatorname {{\mathrm {gr}}} U_D^1}$ and on ![]() $\frak {g}_{\mathbb {F}_{q}}$. In practice, we need a basis of
$\frak {g}_{\mathbb {F}_{q}}$. In practice, we need a basis of ![]() $\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_q}$ consisting of eigenvectors for the action of
$\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_q}$ consisting of eigenvectors for the action of ![]() $\mathbb {F}_{q^2}^{\times }$. Note that
$\mathbb {F}_{q^2}^{\times }$. Note that ![]() $e_j$ and
$e_j$ and ![]() $f_j$ are only eigenvectors for the action of
$f_j$ are only eigenvectors for the action of ![]() $\mathbb {F}_q^{\times }$, but not for
$\mathbb {F}_q^{\times }$, but not for ![]() $\mathbb {F}_{q^2}^{\times }$.
$\mathbb {F}_{q^2}^{\times }$.
Choose an embedding ![]() $\mathbb {F}_{q^2}\hookrightarrow \mathbb {F}$ which extends the fixed embedding
$\mathbb {F}_{q^2}\hookrightarrow \mathbb {F}$ which extends the fixed embedding ![]() $\sigma _0:\mathbb {F}_q\hookrightarrow \mathbb {F}$; we again denote it by
$\sigma _0:\mathbb {F}_q\hookrightarrow \mathbb {F}$; we again denote it by ![]() $\sigma _0$ and let
$\sigma _0$ and let ![]() $\sigma _j=\sigma _0\circ \varphi ^j$ for
$\sigma _j=\sigma _0\circ \varphi ^j$ for ![]() $0\leq j\leq 2f-1$.
$0\leq j\leq 2f-1$.
For ![]() $0\leq j\leq 2f-1$, define the following elements in
$0\leq j\leq 2f-1$, define the following elements in ![]() $\mathbb {F}[\![U_D^1/Z_D^1]\!]$:
$\mathbb {F}[\![U_D^1/Z_D^1]\!]$:
 \[ Y_j:=\sum_{\lambda\in\mathbb{F}_{q^2}^{\times}}\sigma_j(\lambda)^{-1}(1+\varpi_D[\lambda]), \]
\[ Y_j:=\sum_{\lambda\in\mathbb{F}_{q^2}^{\times}}\sigma_j(\lambda)^{-1}(1+\varpi_D[\lambda]), \]
where the term ![]() $1+\varpi _D[\lambda ]$ is considered as an element in the group
$1+\varpi _D[\lambda ]$ is considered as an element in the group ![]() $U_D^1/Z_D^1$. Since
$U_D^1/Z_D^1$. Since ![]() $\sum _{\lambda \in \mathbb {F}_{q^2}^{\times }}\sigma _{j}(\lambda )^{-1}=0$, we have
$\sum _{\lambda \in \mathbb {F}_{q^2}^{\times }}\sigma _{j}(\lambda )^{-1}=0$, we have ![]() $Y_j\in \mathfrak {m}_{D}$. If
$Y_j\in \mathfrak {m}_{D}$. If ![]() $\mu \in \mathbb {F}_{q^2}^{\times }$, then one checks that
$\mu \in \mathbb {F}_{q^2}^{\times }$, then one checks that
where ![]() $\alpha _j:\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ denotes the character defined by
$\alpha _j:\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ denotes the character defined by
Note that ![]() $\alpha _{j+f}=\alpha _j^q=\alpha _j^{-1}$.
$\alpha _{j+f}=\alpha _j^q=\alpha _j^{-1}$.
For ![]() $0\leq j\leq 2f-1$, let
$0\leq j\leq 2f-1$, let ![]() $y_j:= Y_j+ \frak {m}_D^2 \in \operatorname {{\mathrm {gr}}}^1_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$.
$y_j:= Y_j+ \frak {m}_D^2 \in \operatorname {{\mathrm {gr}}}^1_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$.
(i) The elements
 $\{Y_j, 0\leq j\leq 2f-1\}$ generate the ideal
$\{Y_j, 0\leq j\leq 2f-1\}$ generate the ideal  $\mathfrak {m}_{D}$.
$\mathfrak {m}_{D}$.(ii) The elements
 $\{y_j, 0\leq j\leq 2f-1\}$ form a basis of
$\{y_j, 0\leq j\leq 2f-1\}$ form a basis of  $\operatorname {{\mathrm {gr}}}^1_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$.
$\operatorname {{\mathrm {gr}}}^1_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$.
Proof. (i) This is equivalent to checking that the images of ![]() $Y_j$ in
$Y_j$ in ![]() $\mathfrak {m}_{D}/\mathfrak {m}_{D}^2$ are linearly independent (over
$\mathfrak {m}_{D}/\mathfrak {m}_{D}^2$ are linearly independent (over ![]() $\mathbb {F}$). This is proved by a standard technique; see the proof of [Reference SchraenSchr15, Proposition 2.13] for a similar argument.
$\mathbb {F}$). This is proved by a standard technique; see the proof of [Reference SchraenSchr15, Proposition 2.13] for a similar argument.
(ii) This is clear, because ![]() $\operatorname {{\mathrm {gr}}}^1_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ has dimension
$\operatorname {{\mathrm {gr}}}^1_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ has dimension ![]() $2f$ (with a basis
$2f$ (with a basis ![]() $\{e_j,f_j, 0\leq j\leq f-1\}$).
$\{e_j,f_j, 0\leq j\leq f-1\}$).
Lemma 2.8 For ![]() $g\in U_D^i/(U_D^i\cap Z_D^1)$ and
$g\in U_D^i/(U_D^i\cap Z_D^1)$ and ![]() $h\in U_D^j/(U_D^j\cap Z_D^1)$, we have
$h\in U_D^j/(U_D^j\cap Z_D^1)$, we have
Proof. Using Lemma 2.4, this is a consequence of the equality ![]() $(g-1)(h-1)=(gh-1)- (g-1)-(h-1)$.
$(g-1)(h-1)=(gh-1)- (g-1)-(h-1)$.
For ![]() $t\in \mathbb {F}_{q^2}^{\times }$, write
$t\in \mathbb {F}_{q^2}^{\times }$, write
Note that ![]() $\omega (g_t)=1$, so
$\omega (g_t)=1$, so ![]() $g_t-1\in \mathfrak {m}_D^2$ by Lemma 2.4. Let
$g_t-1\in \mathfrak {m}_D^2$ by Lemma 2.4. Let ![]() $u_t$ denote the image of
$u_t$ denote the image of ![]() $g_t-1$ in
$g_t-1$ in ![]() $\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$.
$\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$.
(i) We have
 $[y_i,y_j]=0$ for any pair
$[y_i,y_j]=0$ for any pair  $(i,j)$ with
$(i,j)$ with  $i-j\neq f$ (in
$i-j\neq f$ (in  $\mathbb {Z}/2f\mathbb {Z}$).
$\mathbb {Z}/2f\mathbb {Z}$).(ii) Set
 $h_j':=[y_j,y_{f+j}]$ for
$h_j':=[y_j,y_{f+j}]$ for  $0\leq j\le f-1$. Then
$0\leq j\le f-1$. Then  $\{h_j',\ 0\leq j\leq f-1\}$ are linearly independent in
$\{h_j',\ 0\leq j\leq f-1\}$ are linearly independent in  $\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ and they span the same subspace as
$\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ and they span the same subspace as  $\{h_j, 0\leq j\leq f-1\}$.
$\{h_j, 0\leq j\leq f-1\}$.
Proof. A direct computation shows
 \[ Y_iY_{j}=\sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}}\sigma_i(\lambda)^{-1} \sigma_{j}(\mu)^{-1} (1+\varpi_D[\lambda]+\varpi_D[\mu]+p[\lambda^{q}\mu]). \]
\[ Y_iY_{j}=\sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}}\sigma_i(\lambda)^{-1} \sigma_{j}(\mu)^{-1} (1+\varpi_D[\lambda]+\varpi_D[\mu]+p[\lambda^{q}\mu]). \]
We may write (in ![]() $U_D^1$)
$U_D^1$)
with ![]() $x\in \varpi _D^3\mathcal {O}_D$ and note that
$x\in \varpi _D^3\mathcal {O}_D$ and note that ![]() $(1+p[\lambda ^q\mu ]+x)-1$ has the same image as
$(1+p[\lambda ^q\mu ]+x)-1$ has the same image as ![]() $(1+p[\lambda ^q\mu ])-1$ in
$(1+p[\lambda ^q\mu ])-1$ in ![]() $\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ by Lemma 2.8. Using Lemma 2.8 again, we have
$\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ by Lemma 2.8. Using Lemma 2.8 again, we have
where ![]() $h_{\lambda,\mu }:=1+\varpi _D[\lambda ]+\varpi _D[\mu ]$ and
$h_{\lambda,\mu }:=1+\varpi _D[\lambda ]+\varpi _D[\mu ]$ and ![]() $g_{\lambda ^q\mu }$ is defined by (2.9). Similarly, we have
$g_{\lambda ^q\mu }$ is defined by (2.9). Similarly, we have
 \begin{align*} Y_jY_i\equiv\sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}}\sigma_i(\lambda)^{-1}\sigma_{j}(\mu)^{-1} ((h_{\lambda,\mu}-1)+(g_{\lambda\mu^q}-1))\mod \mathfrak{m}_D^3 \end{align*}
\begin{align*} Y_jY_i\equiv\sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}}\sigma_i(\lambda)^{-1}\sigma_{j}(\mu)^{-1} ((h_{\lambda,\mu}-1)+(g_{\lambda\mu^q}-1))\mod \mathfrak{m}_D^3 \end{align*}
and so
 \[ [Y_i,Y_j]\equiv \sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}} \sigma_i(\lambda)^{-1}\sigma_j(\mu)^{-1}((g_{\lambda^q\mu}-1)-(g_{\lambda\mu^q}-1))\mod \mathfrak{m}_D^3. \]
\[ [Y_i,Y_j]\equiv \sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}} \sigma_i(\lambda)^{-1}\sigma_j(\mu)^{-1}((g_{\lambda^q\mu}-1)-(g_{\lambda\mu^q}-1))\mod \mathfrak{m}_D^3. \]
Taking the image in ![]() $\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ and noting that
$\operatorname {{\mathrm {gr}}}^2_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$ and noting that ![]() $\sigma _i(\lambda )=\sigma _{i-f}(\lambda ^q)$, we obtain
$\sigma _i(\lambda )=\sigma _{i-f}(\lambda ^q)$, we obtain
 \[ [y_i,y_{j}]=\sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}} \frac{\sigma_j(\lambda^q)}{\sigma_{i-f}(\lambda^q)} \sigma_{j}(\lambda^q\mu)^{-1}(u_{\lambda^q\mu}-u_{\lambda\mu^q}). \]
\[ [y_i,y_{j}]=\sum_{\lambda,\mu\in\mathbb{F}_{q^2}^{\times}} \frac{\sigma_j(\lambda^q)}{\sigma_{i-f}(\lambda^q)} \sigma_{j}(\lambda^q\mu)^{-1}(u_{\lambda^q\mu}-u_{\lambda\mu^q}). \]
The map
is surjective and each fibre is bijective to ![]() $\mathbb {F}_{q^2}^{\times }$ (by projecting to the second component), thus
$\mathbb {F}_{q^2}^{\times }$ (by projecting to the second component), thus
 \[ [y_i,y_{j}]=\sum_{t\in\mathbb{F}_{q^2}^{\times}} \bigg(\sum_{\lambda\in\mathbb{F}_{q^2}^{\times}} \frac{\sigma_j(\lambda^q)}{\sigma_{i-f}(\lambda^q)}\bigg)\cdot \sigma_j(t)^{-1}(u_{t}-u_{t^q}). \]
\[ [y_i,y_{j}]=\sum_{t\in\mathbb{F}_{q^2}^{\times}} \bigg(\sum_{\lambda\in\mathbb{F}_{q^2}^{\times}} \frac{\sigma_j(\lambda^q)}{\sigma_{i-f}(\lambda^q)}\bigg)\cdot \sigma_j(t)^{-1}(u_{t}-u_{t^q}). \]
If ![]() $i-j\neq f$, then
$i-j\neq f$, then ![]() $\sum _{\lambda \in \mathbb {F}_{q^2}^{\times }} ({\sigma _j(\lambda ^q)}/{\sigma _{i-f}(\lambda ^q)})=0$ and so
$\sum _{\lambda \in \mathbb {F}_{q^2}^{\times }} ({\sigma _j(\lambda ^q)}/{\sigma _{i-f}(\lambda ^q)})=0$ and so ![]() $[y_i,y_{j}]=0$, proving part (i). If
$[y_i,y_{j}]=0$, proving part (i). If ![]() $i-j=f$, then the last sum equals to
$i-j=f$, then the last sum equals to ![]() $-1$, and so
$-1$, and so
 \[ [y_{j+f},y_j]=-\sum_{t\in\mathbb{F}_{q^2}^{\times}}\sigma_j(t)^{-1}(u_t-u_{t^q}). \]
\[ [y_{j+f},y_j]=-\sum_{t\in\mathbb{F}_{q^2}^{\times}}\sigma_j(t)^{-1}(u_t-u_{t^q}). \]
To prove part (ii), one could argue as in Lemma 2.7, but this needs to make explicit the ![]() $h_j$. Nonetheless, we can conclude by the following observation: since
$h_j$. Nonetheless, we can conclude by the following observation: since ![]() $y_i$ lies in
$y_i$ lies in ![]() $\bigoplus _{0\leq j\leq f-1}(\mathbb {F} e_j\oplus \mathbb {F} f_j)$,
$\bigoplus _{0\leq j\leq f-1}(\mathbb {F} e_j\oplus \mathbb {F} f_j)$, ![]() $[y_i,y_j]$ lies in the subspace spanned by
$[y_i,y_j]$ lies in the subspace spanned by ![]() $h_j=[e_j,f_j]$ (recall
$h_j=[e_j,f_j]$ (recall ![]() $[e_i,e_j]=[e_i,f_j] = [f_i,f_j]=0$ whenever
$[e_i,e_j]=[e_i,f_j] = [f_i,f_j]=0$ whenever ![]() $i\neq j$), and vice versa by part (i) and Lemma 2.7(ii).
$i\neq j$), and vice versa by part (i) and Lemma 2.7(ii).
To make the notation more transparent, we write ![]() $z_i:=y_{i+f}$ for
$z_i:=y_{i+f}$ for ![]() $0\leq i\leq f-1$. Lemma 2.7 and Proposition 2.9 imply that the Lie algebra
$0\leq i\leq f-1$. Lemma 2.7 and Proposition 2.9 imply that the Lie algebra ![]() $\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_q}$ has another basis over
$\mathbb {F}\otimes _{\mathbb {F}_p}\frak {g}_{\mathbb {F}_q}$ has another basis over ![]() $\mathbb {F}$ given by
$\mathbb {F}$ given by ![]() $\{y_j,z_j,h_j'; 0\leq j\leq f-1\}$, with
$\{y_j,z_j,h_j'; 0\leq j\leq f-1\}$, with ![]() $y_j$ and
$y_j$ and ![]() $z_j$ in degree
$z_j$ in degree ![]() $1$,
$1$, ![]() $h_j'$ in degree
$h_j'$ in degree ![]() $2$ and satisfying the relations
$2$ and satisfying the relations
Let ![]() $I_D$ be the left ideal of
$I_D$ be the left ideal of ![]() $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$ generated by the degree-two elements
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$ generated by the degree-two elements ![]() $y_jz_j$ and
$y_jz_j$ and ![]() $h'_j$ for all
$h'_j$ for all ![]() $0\leq j\leq f-1$. The ideal
$0\leq j\leq f-1$. The ideal ![]() $I_D$ is, in fact, a two-sided ideal of
$I_D$ is, in fact, a two-sided ideal of ![]() $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$; it is also the left ideal generated by
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!]$; it is also the left ideal generated by ![]() $(y_j z_j, h_j;\ 0\leq j \leq f-1)$ by Proposition 2.9(ii).
$(y_j z_j, h_j;\ 0\leq j \leq f-1)$ by Proposition 2.9(ii).
(i) The sequence
 $(h_0',\ldots,h_{f-1}')$ is a regular sequence of central elements of
$(h_0',\ldots,h_{f-1}')$ is a regular sequence of central elements of  $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$. The quotient
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$. The quotient  $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]/(h_0',\ldots,h_{f-1}')$ is commutative and is isomorphic to the polynomial ring
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]/(h_0',\ldots,h_{f-1}')$ is commutative and is isomorphic to the polynomial ring  $\mathbb {F}[y_j,z_j;0\leq j\leq f-1]$.
$\mathbb {F}[y_j,z_j;0\leq j\leq f-1]$.(ii) The quotient
 $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!] / I_D$ is isomorphic to
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D} \mathbb {F}[\![ U^1_D /Z^1_D ]\!] / I_D$ is isomorphic to  $\mathbb {F} [y_j,z_j; 0\leq j\leq f-1]/(y_jz_j; 0\leq j \leq f-1)$.
$\mathbb {F} [y_j,z_j; 0\leq j\leq f-1]/(y_jz_j; 0\leq j \leq f-1)$.
Proof. The proof of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Theorem 5.3.4] goes through by the above discussion.
Let ![]() $\chi : \mathcal {O}_D^{\times } \to \mathbb {F}^{\times }$ be a smooth character. Let
$\chi : \mathcal {O}_D^{\times } \to \mathbb {F}^{\times }$ be a smooth character. Let ![]() $\operatorname {{\mathrm {Proj}}}_{\mathbb {F}[\![\mathcal {O}_{D}^{\times } / Z^1_D ]\!]} \chi$ denote the projective envelope of
$\operatorname {{\mathrm {Proj}}}_{\mathbb {F}[\![\mathcal {O}_{D}^{\times } / Z^1_D ]\!]} \chi$ denote the projective envelope of ![]() $\chi$ in the category of
$\chi$ in the category of ![]() $\mathbb {F}[\![\mathcal {O}_{D}^{\times } / Z^1_D]\!]$-modules. For
$\mathbb {F}[\![\mathcal {O}_{D}^{\times } / Z^1_D]\!]$-modules. For ![]() $n\geq 1$, let
$n\geq 1$, let
It is clear that ![]() $W_{\chi,n}\cong \chi \otimes W_{\mathbf {1},n}$, where
$W_{\chi,n}\cong \chi \otimes W_{\mathbf {1},n}$, where ![]() $\mathbf {1}$ denotes the trivial character. The module
$\mathbf {1}$ denotes the trivial character. The module ![]() $W_{\chi,3}$ is of particular importance to us.
$W_{\chi,3}$ is of particular importance to us.
Corollary 2.11 The module ![]() $W_{\mathbf {1},3}$ has the following graded structure:
$W_{\mathbf {1},3}$ has the following graded structure:
 \begin{gather*} \operatorname{{\mathrm{gr}}}^0 W_{\mathbf{1},3} = \mathbb{F},\quad \operatorname{{\mathrm{gr}}}^1W_{\mathbf{1},3} = \bigoplus_{i=0}^{f-1}\mathbb{F}\alpha_i \oplus \mathbb{F}\alpha_i^{-1},\\ \operatorname{{\mathrm{gr}}}^2 W_{\mathbf{1},3} = \mathbb{F}^{2f}\oplus \bigoplus_{0\leq i\leq j\leq f-1}\mathbb{F}\alpha_i\alpha_j\oplus \bigoplus_{0\leq i\leq j\leq f-1}\mathbb{F}\alpha_{i}^{-1}\alpha_{j}^{-1}\oplus \bigoplus_{0\leq i\neq j\leq f-1} \mathbb{F}\alpha_i\alpha_j^{-1}, \end{gather*}
\begin{gather*} \operatorname{{\mathrm{gr}}}^0 W_{\mathbf{1},3} = \mathbb{F},\quad \operatorname{{\mathrm{gr}}}^1W_{\mathbf{1},3} = \bigoplus_{i=0}^{f-1}\mathbb{F}\alpha_i \oplus \mathbb{F}\alpha_i^{-1},\\ \operatorname{{\mathrm{gr}}}^2 W_{\mathbf{1},3} = \mathbb{F}^{2f}\oplus \bigoplus_{0\leq i\leq j\leq f-1}\mathbb{F}\alpha_i\alpha_j\oplus \bigoplus_{0\leq i\leq j\leq f-1}\mathbb{F}\alpha_{i}^{-1}\alpha_{j}^{-1}\oplus \bigoplus_{0\leq i\neq j\leq f-1} \mathbb{F}\alpha_i\alpha_j^{-1}, \end{gather*}
where ![]() $\alpha _j:\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ is the character defined in (2.8).
$\alpha _j:\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ is the character defined in (2.8).
Proof. It follows from Corollary 2.10 using (2.7); cf. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, (44)].
We have the following criterion which allows us to control the Gelfand–Kirillov dimension of an admissible smooth ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $\mathcal {O}_D^{\times }/Z_D^1$. It is an analogue of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Corollary 5.3.5]. Let
$\mathcal {O}_D^{\times }/Z_D^1$. It is an analogue of [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Corollary 5.3.5]. Let ![]() $\overline {W}_{\chi,3}$ denote the quotient of
$\overline {W}_{\chi,3}$ denote the quotient of ![]() $W_{\chi,3}$ by the sum of characters which occur in
$W_{\chi,3}$ by the sum of characters which occur in ![]() $\operatorname {{\mathrm {gr}}}^2W_{\chi,3}$ and non-isomorphic to
$\operatorname {{\mathrm {gr}}}^2W_{\chi,3}$ and non-isomorphic to ![]() $\chi$. For example, if
$\chi$. For example, if ![]() $L=\mathbb {Q}_p$, then
$L=\mathbb {Q}_p$, then ![]() $\dim _{\mathbb {F}}\overline {W}_{\chi,3}=5$ and has a socle filtration as follows (with
$\dim _{\mathbb {F}}\overline {W}_{\chi,3}=5$ and has a socle filtration as follows (with ![]() $\alpha =\alpha _0$):
$\alpha =\alpha _0$):
Corollary 2.12 Let ![]() $\pi$ be an admissible smooth representation of
$\pi$ be an admissible smooth representation of ![]() $\mathcal {O}_D^{\times } / Z_D^1$ over
$\mathcal {O}_D^{\times } / Z_D^1$ over ![]() $\mathbb {F}$. Assume for each character
$\mathbb {F}$. Assume for each character ![]() $\chi$ such that
$\chi$ such that ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi, \pi ) \neq 0$, the natural injection
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi, \pi ) \neq 0$, the natural injection
is an isomorphism. Then ![]() $\dim _{\mathcal {O}_{D}^{\times }} (\pi ) \leq f$, where
$\dim _{\mathcal {O}_{D}^{\times }} (\pi ) \leq f$, where ![]() $\dim _{\mathcal {O}_{D}^{\times }}(\pi )$ is the Gelfand–Kirillov dimension of
$\dim _{\mathcal {O}_{D}^{\times }}(\pi )$ is the Gelfand–Kirillov dimension of ![]() $\pi$ over
$\pi$ over ![]() $\mathcal {O}_{D}^{\times }$.
$\mathcal {O}_{D}^{\times }$.
Proof. The Pontryagin dual ![]() $\pi ^{\vee }$ is naturally a finitely generated module over
$\pi ^{\vee }$ is naturally a finitely generated module over ![]() $\mathbb {F}[\![U_D^1/Z_D^1]\!]$ as
$\mathbb {F}[\![U_D^1/Z_D^1]\!]$ as ![]() $\pi$ is admissible, so the graded module
$\pi$ is admissible, so the graded module ![]() $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}(\pi ^{\vee })$ is finitely generated over
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}(\pi ^{\vee })$ is finitely generated over ![]() $\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$. The condition (2.11) implies that
$\operatorname {{\mathrm {gr}}}_{\mathfrak {m}_D}\mathbb {F}[\![U_D^1/Z_D^1]\!]$. The condition (2.11) implies that ![]() $\operatorname {{\mathrm {gr}}}^0_{\frak {m}_D} (\pi ^{\vee })$ is killed by
$\operatorname {{\mathrm {gr}}}^0_{\frak {m}_D} (\pi ^{\vee })$ is killed by ![]() $y_jz_j$ and
$y_jz_j$ and ![]() $h_j'$ (for
$h_j'$ (for ![]() $1\leq j\leq f-1$), hence also by
$1\leq j\leq f-1$), hence also by ![]() $I_D$. The result then follows from Corollary 2.10; see [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Corollary 5.3.5] for details.
$I_D$. The result then follows from Corollary 2.10; see [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Corollary 5.3.5] for details.
2.4  $\operatorname {{\mathrm {Ext}}}^i$ groups when
$\operatorname {{\mathrm {Ext}}}^i$ groups when  $L=\mathbb {Q}_p$
$L=\mathbb {Q}_p$
We assume ![]() $L=\mathbb {Q}_p$ with
$L=\mathbb {Q}_p$ with ![]() $p\geq 5$. We write
$p\geq 5$. We write ![]() $\alpha =\alpha _0$.
$\alpha =\alpha _0$.
Proposition 2.13 Let ![]() $\psi,\chi :\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ be two smooth characters. Then
$\psi,\chi :\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ be two smooth characters. Then ![]() $\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}^{\times }_D/Z_D^1}(\psi,\chi )$ is nonzero if and only if
$\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}^{\times }_D/Z_D^1}(\psi,\chi )$ is nonzero if and only if ![]() $\psi =\chi \alpha$ or
$\psi =\chi \alpha$ or ![]() $\psi =\chi \alpha ^{-1}$. Moreover,
$\psi =\chi \alpha ^{-1}$. Moreover,
Proof. This is a consequence of Corollary 2.11.
Proposition 2.14 Let ![]() $\tau _1,\tau _2$ be finite-dimensional smooth representations of
$\tau _1,\tau _2$ be finite-dimensional smooth representations of ![]() $\mathcal {O}_D^{\times }/Z_D^1$. Then there is an isomorphism
$\mathcal {O}_D^{\times }/Z_D^1$. Then there is an isomorphism ![]() $\operatorname {{\mathrm {Ext}}}^i_{\mathcal {O}_D^{\times }/Z_D^1}(\tau _1,\tau _2)\cong \operatorname {{\mathrm {Ext}}}^{3-i}_{\mathcal {O}_D^{\times }/Z_D^1}(\tau _2,\tau _1)^{\vee }$ for
$\operatorname {{\mathrm {Ext}}}^i_{\mathcal {O}_D^{\times }/Z_D^1}(\tau _1,\tau _2)\cong \operatorname {{\mathrm {Ext}}}^{3-i}_{\mathcal {O}_D^{\times }/Z_D^1}(\tau _2,\tau _1)^{\vee }$ for ![]() $0\leq i\leq 3$.
$0\leq i\leq 3$.
Proof. First, we have isomorphisms
Second, since ![]() $U_D^1/Z_D^1$ is a Poincaré group of dimension three (cf. [Reference SerreSer02, § 4.5]), Poincaré duality induces an isomorphism
$U_D^1/Z_D^1$ is a Poincaré group of dimension three (cf. [Reference SerreSer02, § 4.5]), Poincaré duality induces an isomorphism
for ![]() $0\leq i\leq 3$ and any finite-dimensional representation
$0\leq i\leq 3$ and any finite-dimensional representation ![]() $\tau$. The result easily follows.
$\tau$. The result easily follows.
3. Lattices in some locally algebraic representations of  $\mathrm {GL}_2(\mathbb {Z}_p)$
$\mathrm {GL}_2(\mathbb {Z}_p)$
Let ![]() $K: = \mathrm {GL}_2(\mathbb {Z}_p)$,
$K: = \mathrm {GL}_2(\mathbb {Z}_p)$, ![]() $\Gamma : = \mathrm {GL}_2(\mathbb {F}_p)$, and
$\Gamma : = \mathrm {GL}_2(\mathbb {F}_p)$, and ![]() $K_1: = \operatorname {{\mathrm {Ker}}}(K \twoheadrightarrow \Gamma )$. Let
$K_1: = \operatorname {{\mathrm {Ker}}}(K \twoheadrightarrow \Gamma )$. Let ![]() $I$ (respectively,
$I$ (respectively, ![]() $I_1$) denote the upper Iwahori (respectively, pro-
$I_1$) denote the upper Iwahori (respectively, pro-![]() $p$ Iwahori) subgroup of
$p$ Iwahori) subgroup of ![]() $K$. Let
$K$. Let ![]() $Z$ denote the centre of
$Z$ denote the centre of ![]() $G$,
$G$, ![]() $Z_1 : = Z\cap K_1$. Let
$Z_1 : = Z\cap K_1$. Let
Let ![]() $\alpha : H \to \mathbb {F}^{\times }$ be the character of
$\alpha : H \to \mathbb {F}^{\times }$ be the character of ![]() $H$ sending
$H$ sending ![]() $\big (\begin{smallmatrix} [a] & 0 \\ 0 & [d] \end{smallmatrix}\big )$ to
$\big (\begin{smallmatrix} [a] & 0 \\ 0 & [d] \end{smallmatrix}\big )$ to ![]() $a d^{-1}$. By abuse of notation we also denote the image of
$a d^{-1}$. By abuse of notation we also denote the image of ![]() $H$ in
$H$ in ![]() $\Gamma$ by the same letter. If
$\Gamma$ by the same letter. If ![]() $\chi$ is a character of
$\chi$ is a character of ![]() $H$, we denote by
$H$, we denote by ![]() $\chi ^s$ the character sending
$\chi ^s$ the character sending ![]() $h$ to
$h$ to ![]() $\chi (shs)$, where
$\chi (shs)$, where ![]() $s:=\big (\begin{smallmatrix} {0} & {1}\\ {1} & {0}\end{smallmatrix}\big )$. We regard a character of
$s:=\big (\begin{smallmatrix} {0} & {1}\\ {1} & {0}\end{smallmatrix}\big )$. We regard a character of ![]() $H$ as a character of
$H$ as a character of ![]() $I$ via the quotient map
$I$ via the quotient map ![]() $I\twoheadrightarrow H$; note that any smooth
$I\twoheadrightarrow H$; note that any smooth ![]() $\mathbb {F}$-valued character of
$\mathbb {F}$-valued character of ![]() $I$ arises in this way.
$I$ arises in this way.
For ![]() $m,n\in \mathbb {N}$, we denote
$m,n\in \mathbb {N}$, we denote
which are naturally representations of ![]() $\Gamma$ over
$\Gamma$ over ![]() $\mathbb {F}$. We also regard them as representations of
$\mathbb {F}$. We also regard them as representations of ![]() $K$ via the natural projection
$K$ via the natural projection ![]() $K\twoheadrightarrow \Gamma$. Up to isomorphism the set
$K\twoheadrightarrow \Gamma$. Up to isomorphism the set ![]() $\{\sigma _{m,n},\ 0\leq m \leq p-1,\ 0\leq n \leq p-2\}$ forms a complete list of irreducible representations of
$\{\sigma _{m,n},\ 0\leq m \leq p-1,\ 0\leq n \leq p-2\}$ forms a complete list of irreducible representations of ![]() $\Gamma$ (and of
$\Gamma$ (and of ![]() $K$) over
$K$) over ![]() $\mathbb {F}$.
$\mathbb {F}$.
We choose the standard basis of ![]() $\sigma _{m,n}$ to be
$\sigma _{m,n}$ to be ![]() $\{X^iY^{m-i};\ 0\leq i\leq m\}$, with the action of
$\{X^iY^{m-i};\ 0\leq i\leq m\}$, with the action of ![]() $\Gamma$ given by
$\Gamma$ given by
It is well-known that ![]() $\sigma _{m,n}^{I_1}$ is one-dimensional (spanned by
$\sigma _{m,n}^{I_1}$ is one-dimensional (spanned by ![]() $X^m$), on which
$X^m$), on which ![]() $H$ acts via the character sending
$H$ acts via the character sending ![]() $\big (\begin{smallmatrix} {[a]} & 0 \\ 0 & {[d]} \end{smallmatrix}\big )$ to
$\big (\begin{smallmatrix} {[a]} & 0 \\ 0 & {[d]} \end{smallmatrix}\big )$ to ![]() $a^{m+n} d^n$, which we denote by
$a^{m+n} d^n$, which we denote by ![]() $\chi _{m,n}$. Similarly, the space of coinvariants
$\chi _{m,n}$. Similarly, the space of coinvariants ![]() $(\sigma _{m,n})_{I_1}$ is one-dimensional on which
$(\sigma _{m,n})_{I_1}$ is one-dimensional on which ![]() $H$ acts via
$H$ acts via ![]() $\chi _{m,n}^s$.
$\chi _{m,n}^s$.
Recall ![]() $E := W(\mathbb {F})[1/p]$, where
$E := W(\mathbb {F})[1/p]$, where ![]() $\mathcal {O}:=W(\mathbb {F})$ is the ring of Witt vectors in
$\mathcal {O}:=W(\mathbb {F})$ is the ring of Witt vectors in ![]() $\mathbb {F}$. If
$\mathbb {F}$. If ![]() $V$ is a finite-dimensional representation of
$V$ is a finite-dimensional representation of ![]() $K$ over
$K$ over ![]() $E$, then
$E$, then ![]() $V^{\circ }$ will denote a
$V^{\circ }$ will denote a ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $V$ and
$V$ and ![]() $\overline {V^{\circ }}$ its reduction modulo
$\overline {V^{\circ }}$ its reduction modulo ![]() $p$. We will write
$p$. We will write ![]() $\overline {V}^{\rm ss}$ for the semisimplification of
$\overline {V}^{\rm ss}$ for the semisimplification of ![]() $\overline {V^{\circ }}$. Following [Reference Emerton, Gee and SavittEGS15], we say
$\overline {V^{\circ }}$. Following [Reference Emerton, Gee and SavittEGS15], we say ![]() $V$ is residually multiplicity free if any of the Jordan–Hölder factors of
$V$ is residually multiplicity free if any of the Jordan–Hölder factors of ![]() $\overline {V}^{\rm ss}$ occurs with multiplicity one. In this section, a lattice always means a
$\overline {V}^{\rm ss}$ occurs with multiplicity one. In this section, a lattice always means a ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice.
$\mathcal {O}$-lattice.
3.1 Preliminaries
Denote by ![]() $U(\mathbb {Z}_p)$ (respectively,
$U(\mathbb {Z}_p)$ (respectively, ![]() $B(\mathbb {Z}_p)$) the (upper) unipotent (respectively, Borel) subgroup of
$B(\mathbb {Z}_p)$) the (upper) unipotent (respectively, Borel) subgroup of ![]() $K$. Note that
$K$. Note that ![]() $H$ normalizes
$H$ normalizes ![]() $U(\mathbb {Z}_p)$.
$U(\mathbb {Z}_p)$.
Proposition 3.1 Let ![]() $W$ be a finite-dimensional
$W$ be a finite-dimensional ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $B(\mathbb {Z}_p)$, of dimension
$B(\mathbb {Z}_p)$, of dimension ![]() $\geq 2$.
$\geq 2$.
(i) Assume that
 $W^{U(\mathbb {Z}_p)}$ is one-dimensional and isomorphic to
$W^{U(\mathbb {Z}_p)}$ is one-dimensional and isomorphic to  $\chi$ as an
$\chi$ as an  $H$-representation. Then
$H$-representation. Then
 \[ (\mathrm{Sym}^{1}\mathbb{F}^2\otimes W)^{U(\mathbb{Z}_p)}\cong \chi\chi_{1,0}\oplus \chi\chi_{1,0}^s. \]
\[ (\mathrm{Sym}^{1}\mathbb{F}^2\otimes W)^{U(\mathbb{Z}_p)}\cong \chi\chi_{1,0}\oplus \chi\chi_{1,0}^s. \]
(ii) Assume that
 $W_{U(\mathbb {Z}_p)}$ is one-dimensional and isomorphic to
$W_{U(\mathbb {Z}_p)}$ is one-dimensional and isomorphic to  $\chi$ as an
$\chi$ as an  $H$-representation. Then
$H$-representation. Then
 \[ (\mathrm{Sym}^1\mathbb{F}^2\otimes W)_{U(\mathbb{Z}_p)}\cong\chi\chi_{1,0}\oplus \chi\chi_{1,0}^s. \]
\[ (\mathrm{Sym}^1\mathbb{F}^2\otimes W)_{U(\mathbb{Z}_p)}\cong\chi\chi_{1,0}\oplus \chi\chi_{1,0}^s. \]
Proof. (i) Let ![]() $W_0:=W^{U(\mathbb {Z}_p)}\cong \chi$. We first prove that
$W_0:=W^{U(\mathbb {Z}_p)}\cong \chi$. We first prove that ![]() $(W/W_0)^{U(\mathbb {Z}_p)}$ is one-dimensional and isomorphic to
$(W/W_0)^{U(\mathbb {Z}_p)}$ is one-dimensional and isomorphic to ![]() $\chi \alpha ^{-1}$ as an
$\chi \alpha ^{-1}$ as an ![]() $H$-representation. Since
$H$-representation. Since ![]() $\dim _{\mathbb {F}}W\geq 2$ by assumption,
$\dim _{\mathbb {F}}W\geq 2$ by assumption, ![]() $W/W_0$ is nonzero, hence
$W/W_0$ is nonzero, hence ![]() $(W/W_0)^{U(\mathbb {Z}_p)}$ is also nonzero because
$(W/W_0)^{U(\mathbb {Z}_p)}$ is also nonzero because ![]() $U(\mathbb {Z}_p)$ is a pro-
$U(\mathbb {Z}_p)$ is a pro-![]() $p$-group. On the other hand, we have an
$p$-group. On the other hand, we have an ![]() $H$-equivariant injection
$H$-equivariant injection
which is actually an isomorphism because ![]() $H^1(U(\mathbb {Z}_p),\chi )\cong \chi \alpha ^{-1}$ is one-dimensional (see, e.g., [Reference PaškūnasPaš10, Lemma 5.5]). This proves the claim.
$H^1(U(\mathbb {Z}_p),\chi )\cong \chi \alpha ^{-1}$ is one-dimensional (see, e.g., [Reference PaškūnasPaš10, Lemma 5.5]). This proves the claim.
Any element ![]() $w\in \mathrm {Sym}^1\mathbb {F}^2\otimes W$ can be written as
$w\in \mathrm {Sym}^1\mathbb {F}^2\otimes W$ can be written as ![]() $Y\otimes w_0+X\otimes w_1$ for (unique)
$Y\otimes w_0+X\otimes w_1$ for (unique) ![]() $w_0,w_1\in W$. Let
$w_0,w_1\in W$. Let ![]() $g=\big (\begin{smallmatrix} {1} & {t}\\ {0} & {1}\end{smallmatrix}\big ) \in U(\mathbb {Z}_p)$. Then
$g=\big (\begin{smallmatrix} {1} & {t}\\ {0} & {1}\end{smallmatrix}\big ) \in U(\mathbb {Z}_p)$. Then
Hence, ![]() $w$ is fixed by
$w$ is fixed by ![]() $U(\mathbb {Z}_p)$ if and only if
$U(\mathbb {Z}_p)$ if and only if
We have two cases.
(a) If
 $w_0=0$, then the above condition becomes
$w_0=0$, then the above condition becomes  $gw_1=w_1$, i.e.
$gw_1=w_1$, i.e.  $w_1\in W_0$.
$w_1\in W_0$.(b) If
 $w_0\neq 0$, then
$w_0\neq 0$, then  $w_0\in W_0$ and
$w_0\in W_0$ and  $w_1\in (W/W_0)^{U(\mathbb {Z}_p)}$. Moreover,
$w_1\in (W/W_0)^{U(\mathbb {Z}_p)}$. Moreover,  $(W/W_0)^{U(\mathbb {Z}_p)}$ is one-dimensional as seen above and the condition
$(W/W_0)^{U(\mathbb {Z}_p)}$ is one-dimensional as seen above and the condition  $gw_1=w_1-\bar {t}w_0$ determines uniquely
$gw_1=w_1-\bar {t}w_0$ determines uniquely  $w_1$ (whenever
$w_1$ (whenever  $w_0\neq 0$ is fixed).
$w_0\neq 0$ is fixed).
The result easily follows.
(ii) This follows from part (i) via the fact that ![]() $(W_{U(\mathbb {Z}_p)})^{\vee }\cong (W^{\vee })^{U(\mathbb {Z}_p)}$, and similarly for
$(W_{U(\mathbb {Z}_p)})^{\vee }\cong (W^{\vee })^{U(\mathbb {Z}_p)}$, and similarly for
Corollary 3.2 Let ![]() $V=\operatorname {{\mathrm {Ind}}}_{I}^{K}\chi$ for some smooth character
$V=\operatorname {{\mathrm {Ind}}}_{I}^{K}\chi$ for some smooth character ![]() $\chi :I\rightarrow \mathbb {F}^{\times }$. Then
$\chi :I\rightarrow \mathbb {F}^{\times }$. Then
 \begin{gather*} (\mathrm{Sym}^1\mathbb{F}^2\otimes V)^{U(\mathbb{Z}_p)}\cong \chi^s\chi_{1,0}\oplus\chi^s\chi_{1,0}^s\oplus \chi\chi_{1,0},\\ (\mathrm{Sym}^1\mathbb{F}^2\otimes V)_{U(\mathbb{Z}_p)}\cong \chi^s\chi_{1,0}\oplus\chi^s\chi_{1,0}^s\oplus \chi\chi_{1,0}^s. \end{gather*}
\begin{gather*} (\mathrm{Sym}^1\mathbb{F}^2\otimes V)^{U(\mathbb{Z}_p)}\cong \chi^s\chi_{1,0}\oplus\chi^s\chi_{1,0}^s\oplus \chi\chi_{1,0},\\ (\mathrm{Sym}^1\mathbb{F}^2\otimes V)_{U(\mathbb{Z}_p)}\cong \chi^s\chi_{1,0}\oplus\chi^s\chi_{1,0}^s\oplus \chi\chi_{1,0}^s. \end{gather*}
Proof. Mackey's decomposition theorem gives an isomorphism ![]() $V|_{I}\cong \chi \oplus V'$, where
$V|_{I}\cong \chi \oplus V'$, where ![]() $V':= \operatorname {{\mathrm {Ind}}}_{HK_1}^{I}\chi ^s$. It is easy to see that
$V':= \operatorname {{\mathrm {Ind}}}_{HK_1}^{I}\chi ^s$. It is easy to see that ![]() $V'$ has dimension
$V'$ has dimension ![]() $p$, and
$p$, and ![]() $V'^{U(\mathbb {Z}_p)}\cong V'_{U(\mathbb {Z}_p)}\cong \chi ^s$. Thus, Proposition 3.1 applies to
$V'^{U(\mathbb {Z}_p)}\cong V'_{U(\mathbb {Z}_p)}\cong \chi ^s$. Thus, Proposition 3.1 applies to ![]() $\mathrm {Sym}^{1}\mathbb {F}^2\otimes V'$. The results then follow by noting that
$\mathrm {Sym}^{1}\mathbb {F}^2\otimes V'$. The results then follow by noting that ![]() $(\mathrm {Sym}^1\mathbb {F}^2\otimes \chi )^{U(\mathbb {Z}_p)}\cong \mathbb {F} X\otimes \chi$ and
$(\mathrm {Sym}^1\mathbb {F}^2\otimes \chi )^{U(\mathbb {Z}_p)}\cong \mathbb {F} X\otimes \chi$ and ![]() $(\mathrm {Sym}^1\mathbb {F}^2\otimes \chi )_{U(\mathbb {Z}_p)}\cong \mathbb {F} Y\otimes \chi$.
$(\mathrm {Sym}^1\mathbb {F}^2\otimes \chi )_{U(\mathbb {Z}_p)}\cong \mathbb {F} Y\otimes \chi$.
Consider the following situation: ![]() $V_1, V_2$ are two irreducible locally algebraic representations of
$V_1, V_2$ are two irreducible locally algebraic representations of ![]() $K$, and
$K$, and ![]() $L_i\subset V_i$ is a lattice for
$L_i\subset V_i$ is a lattice for ![]() $i=1,2$. Assume that we are given an
$i=1,2$. Assume that we are given an ![]() $\mathbb {F}[K]$-module
$\mathbb {F}[K]$-module ![]() $W$, together with
$W$, together with ![]() $K$-equivariant morphisms
$K$-equivariant morphisms ![]() $r_i:L_i\rightarrow W$. Let
$r_i:L_i\rightarrow W$. Let ![]() $L$ be the fibered product of
$L$ be the fibered product of ![]() $r_1$ and
$r_1$ and ![]() $r_2$, namely
$r_2$, namely
Then ![]() $L$ is a lattice in
$L$ is a lattice in ![]() $V_1\oplus V_2$. We also call
$V_1\oplus V_2$. We also call ![]() $L$ the gluing lattice of
$L$ the gluing lattice of ![]() $L_1$ and
$L_1$ and ![]() $L_2$ along
$L_2$ along ![]() $W$. We remark that, if either
$W$. We remark that, if either ![]() $r_1$ or
$r_1$ or ![]() $r_2$ is surjective, then so is
$r_2$ is surjective, then so is ![]() $r_1-r_2$.
$r_1-r_2$.
Lemma 3.3 Assume that ![]() $r_1$ is surjective.
$r_1$ is surjective.
(i) There exists a short exact sequence
 \[ 0\rightarrow \operatorname{{\mathrm{Ker}}}(r_1)/p\operatorname{{\mathrm{Ker}}}(r_1)\rightarrow L/pL\rightarrow L_2/pL_2\rightarrow0. \]
\[ 0\rightarrow \operatorname{{\mathrm{Ker}}}(r_1)/p\operatorname{{\mathrm{Ker}}}(r_1)\rightarrow L/pL\rightarrow L_2/pL_2\rightarrow0. \]
(ii) Let
 $r_L$ denote the composite morphism
$r_L$ denote the composite morphism  $L\rightarrow L/pL\rightarrow L_2/pL_2$, where the second map is as in part (i). Then
$L\rightarrow L/pL\rightarrow L_2/pL_2$, where the second map is as in part (i). Then  $\operatorname {{\mathrm {Ker}}}(r_L)=\operatorname {{\mathrm {Ker}}}(r_1)+pL$ and
$\operatorname {{\mathrm {Ker}}}(r_L)=\operatorname {{\mathrm {Ker}}}(r_1)+pL$ and
 \[ \operatorname{{\mathrm{Ker}}}(r_L)/p\operatorname{{\mathrm{Ker}}}(r_L)\cong \operatorname{{\mathrm{Ker}}}(r_1)/p\operatorname{{\mathrm{Ker}}}(r_1)\oplus pL_2/p^2L_2. \]
\[ \operatorname{{\mathrm{Ker}}}(r_L)/p\operatorname{{\mathrm{Ker}}}(r_L)\cong \operatorname{{\mathrm{Ker}}}(r_1)/p\operatorname{{\mathrm{Ker}}}(r_1)\oplus pL_2/p^2L_2. \]
Proof. (i) We have the following commutative diagram.

By the snake lemma, it induces a short exact sequence ![]() $0\rightarrow \operatorname {{\mathrm {Ker}}}(r_1)\rightarrow L\rightarrow L_2\rightarrow 0$. We obtain the result by taking mod
$0\rightarrow \operatorname {{\mathrm {Ker}}}(r_1)\rightarrow L\rightarrow L_2\rightarrow 0$. We obtain the result by taking mod ![]() $p$ reduction (as
$p$ reduction (as ![]() $L_2$ is
$L_2$ is ![]() $\mathcal {O}$-flat).
$\mathcal {O}$-flat).
(ii) It is clear from part (i) that ![]() $\operatorname {{\mathrm {Ker}}}(r_L)=\operatorname {{\mathrm {Ker}}}(r_1)+pL$, so we have a short exact sequence
$\operatorname {{\mathrm {Ker}}}(r_L)=\operatorname {{\mathrm {Ker}}}(r_1)+pL$, so we have a short exact sequence
Taking mod ![]() $p$ reduction and noting that
$p$ reduction and noting that ![]() $\operatorname {{\mathrm {Ker}}}(r_1)\cap pL=p\operatorname {{\mathrm {Ker}}}(r_1)$ by part (i), we obtain an exact sequence
$\operatorname {{\mathrm {Ker}}}(r_1)\cap pL=p\operatorname {{\mathrm {Ker}}}(r_1)$ by part (i), we obtain an exact sequence
But the map ![]() $p\operatorname {{\mathrm {Ker}}}(r_1)/p^2\operatorname {{\mathrm {Ker}}}(r_1)\rightarrow \operatorname {{\mathrm {Ker}}}(r_1)/p\operatorname {{\mathrm {Ker}}}(r_1)$ is identically zero, so the result follows from part (i).
$p\operatorname {{\mathrm {Ker}}}(r_1)/p^2\operatorname {{\mathrm {Ker}}}(r_1)\rightarrow \operatorname {{\mathrm {Ker}}}(r_1)/p\operatorname {{\mathrm {Ker}}}(r_1)$ is identically zero, so the result follows from part (i).
Lemma 3.4 Assume that both ![]() $r_1$ and
$r_1$ and ![]() $r_2$ are surjective. Assume moreover that:
$r_2$ are surjective. Assume moreover that:
(a)
 $\mathrm {cosoc}(L_1)=\mathrm {cosoc}(W)$;
$\mathrm {cosoc}(L_1)=\mathrm {cosoc}(W)$;(b)
 $\mathrm {cosoc}(\operatorname {{\mathrm {Ker}}}(r_1))$ and
$\mathrm {cosoc}(\operatorname {{\mathrm {Ker}}}(r_1))$ and  $\mathrm {cosoc}(\operatorname {{\mathrm {Ker}}}(r_2))$ do not admit common Jordan–Hölder factors.
$\mathrm {cosoc}(\operatorname {{\mathrm {Ker}}}(r_2))$ do not admit common Jordan–Hölder factors.
Then ![]() $\mathrm {cosoc}(L)\cong \mathrm {cosoc}(L_2)$.
$\mathrm {cosoc}(L)\cong \mathrm {cosoc}(L_2)$.
Proof. We need to show that the natural map
is an isomorphism for any Serre weight ![]() $\sigma$. By applying
$\sigma$. By applying ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}[K]}(-,\sigma )$ to (3.1) we obtain a long exact sequence
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}[K]}(-,\sigma )$ to (3.1) we obtain a long exact sequence
 \begin{align*} 0\rightarrow \operatorname{{\mathrm{Hom}}}(W,\sigma)\rightarrow\operatorname{{\mathrm{Hom}}}(L_1,\sigma)\oplus \operatorname{{\mathrm{Hom}}}(L_2,\sigma) &\rightarrow \operatorname{{\mathrm{Hom}}}(L,\sigma)\\ &\rightarrow \operatorname{{\mathrm{Ext}}}^1(W,\sigma)\rightarrow \operatorname{{\mathrm{Ext}}}^1(L_1,\sigma)\oplus \operatorname{{\mathrm{Ext}}}^1(L_2,\sigma). \end{align*}
\begin{align*} 0\rightarrow \operatorname{{\mathrm{Hom}}}(W,\sigma)\rightarrow\operatorname{{\mathrm{Hom}}}(L_1,\sigma)\oplus \operatorname{{\mathrm{Hom}}}(L_2,\sigma) &\rightarrow \operatorname{{\mathrm{Hom}}}(L,\sigma)\\ &\rightarrow \operatorname{{\mathrm{Ext}}}^1(W,\sigma)\rightarrow \operatorname{{\mathrm{Ext}}}^1(L_1,\sigma)\oplus \operatorname{{\mathrm{Ext}}}^1(L_2,\sigma). \end{align*}
By assumption (a), the surjection ![]() $r_1:L_1\twoheadrightarrow W$ induces an isomorphism
$r_1:L_1\twoheadrightarrow W$ induces an isomorphism ![]() $\operatorname {{\mathrm {Hom}}}(W,\sigma )\xrightarrow {\sim } \operatorname {{\mathrm {Hom}}}(L_1,\sigma )$. To conclude we need to show that the morphism
$\operatorname {{\mathrm {Hom}}}(W,\sigma )\xrightarrow {\sim } \operatorname {{\mathrm {Hom}}}(L_1,\sigma )$. To conclude we need to show that the morphism
is injective. For this, it is enough to prove that either ![]() $\operatorname {{\mathrm {Hom}}}(\operatorname {{\mathrm {Ker}}}(r_1),\sigma )$ or
$\operatorname {{\mathrm {Hom}}}(\operatorname {{\mathrm {Ker}}}(r_1),\sigma )$ or ![]() $\operatorname {{\mathrm {Hom}}}(\operatorname {{\mathrm {Ker}}}(r_2),\sigma )$ vanishes, which is a consequence of assumption (b).
$\operatorname {{\mathrm {Hom}}}(\operatorname {{\mathrm {Ker}}}(r_2),\sigma )$ vanishes, which is a consequence of assumption (b).
Finally, we record a result which will be used later on.
Proposition 3.5 Let ![]() $V$ be an irreducible smooth representation of
$V$ be an irreducible smooth representation of ![]() $K$ over
$K$ over ![]() $E$. Then the
$E$. Then the ![]() $K$-representation
$K$-representation ![]() $\mathrm {Sym}^1 E^2 \otimes V$ is again irreducible.
$\mathrm {Sym}^1 E^2 \otimes V$ is again irreducible.
Proof. This is [Reference Schneider, Teitelbaum and PrasadSTP01, Proposition 3.4].
3.2 Lattices in tame types
We consider the following representations of ![]() $\Gamma$ over
$\Gamma$ over ![]() $E$, and view them as smooth representations of
$E$, and view them as smooth representations of ![]() $K$ via the projection
$K$ via the projection ![]() $K \twoheadrightarrow \Gamma$.
$K \twoheadrightarrow \Gamma$.
• Let
 $\chi _1,\chi _2: \mathbb {F}_{p}^{\times } \to E^{\times }$ be two characters. Let
$\chi _1,\chi _2: \mathbb {F}_{p}^{\times } \to E^{\times }$ be two characters. Let  $I(\chi _1,\chi _2)$ denote the principal series representation
$I(\chi _1,\chi _2)$ denote the principal series representation  $\operatorname {{\mathrm {Ind}}}_{B(\mathbb {F}_p)}^{\Gamma }\chi _1\otimes \chi _2$, where
$\operatorname {{\mathrm {Ind}}}_{B(\mathbb {F}_p)}^{\Gamma }\chi _1\otimes \chi _2$, where  $B(\mathbb {F}_p)$ is the (upper) Borel subgroup of
$B(\mathbb {F}_p)$ is the (upper) Borel subgroup of  $\Gamma$. It is well-known that
$\Gamma$. It is well-known that  $I(\chi _1,\chi _2)$ is irreducible if
$I(\chi _1,\chi _2)$ is irreducible if  $\chi _1 \neq \chi _2$. If
$\chi _1 \neq \chi _2$. If  $\chi _1 =\chi _2 =\chi$, then
where
$\chi _1 =\chi _2 =\chi$, then
where \[ I(\chi, \chi) \cong (\chi \circ\det) \oplus\ ({\rm sp} \otimes\chi\circ\det), \]
\[ I(\chi, \chi) \cong (\chi \circ\det) \oplus\ ({\rm sp} \otimes\chi\circ\det), \]
 ${\rm sp}$ denotes the Steinberg representation.
${\rm sp}$ denotes the Steinberg representation.• Let
 $\psi :\mathbb {F}_{p^2}^{\times } \to E^{\times }$ be a character which does not factor through the norm map
$\psi :\mathbb {F}_{p^2}^{\times } \to E^{\times }$ be a character which does not factor through the norm map  $\mathbb {F}_{p^2}^{\times } \to \mathbb {F}_{p}^{\times }$. This is equivalent to requiring
$\mathbb {F}_{p^2}^{\times } \to \mathbb {F}_{p}^{\times }$. This is equivalent to requiring  $\psi \neq \psi ^p$. There is an irreducible
$\psi \neq \psi ^p$. There is an irreducible  $(p-1)$-dimensional representation
$(p-1)$-dimensional representation  $\Theta (\psi )$ characterized by the isomorphism
$\Theta (\psi )$ characterized by the isomorphism  $\Theta (\psi )\otimes {\rm sp} \cong \operatorname {{\mathrm {Ind}}}_{\mathbb {F}_{p^2}^{\times }}^{\mathrm {GL}_2(\mathbb {F}_p)} \psi$, where
$\Theta (\psi )\otimes {\rm sp} \cong \operatorname {{\mathrm {Ind}}}_{\mathbb {F}_{p^2}^{\times }}^{\mathrm {GL}_2(\mathbb {F}_p)} \psi$, where  $\mathbb {F}_{p^2}^{\times } \hookrightarrow \mathrm {GL}_2(\mathbb {F}_p)$ is a fixed group embedding. For two such characters
$\mathbb {F}_{p^2}^{\times } \hookrightarrow \mathrm {GL}_2(\mathbb {F}_p)$ is a fixed group embedding. For two such characters  $\psi,\psi '$,
$\psi,\psi '$,  $\Theta (\psi ) \cong \Theta (\psi ')$ if and only if
$\Theta (\psi ) \cong \Theta (\psi ')$ if and only if  $\psi '\in \{\psi, \psi ^p\}$.
$\psi '\in \{\psi, \psi ^p\}$.
The Jordan–Hölder factors of the reduction mod ![]() $p$ of any lattice in the above representations are determined in [Reference DiamondDia07]. We recall the results in the next proposition.
$p$ of any lattice in the above representations are determined in [Reference DiamondDia07]. We recall the results in the next proposition.
Let ![]() $x: \mathbb {F}_p \hookrightarrow \mathbb {F}$ denote the natural embedding and
$x: \mathbb {F}_p \hookrightarrow \mathbb {F}$ denote the natural embedding and ![]() $[x]: \mathbb {F}_p \to \mathcal {O}$ be the Teichmüller lift of
$[x]: \mathbb {F}_p \to \mathcal {O}$ be the Teichmüller lift of ![]() $x$ which will be viewed as a multiplicative character of
$x$ which will be viewed as a multiplicative character of ![]() $\mathbb {F}_p^{\times }$. Let
$\mathbb {F}_p^{\times }$. Let ![]() $\xi : \mathbb {F}_{p^2} \hookrightarrow \mathbb {F}$ be an embedding extending
$\xi : \mathbb {F}_{p^2} \hookrightarrow \mathbb {F}$ be an embedding extending ![]() $x$. Let
$x$. Let ![]() $\xi ':= \xi ^p$ and
$\xi ':= \xi ^p$ and ![]() $\zeta : = \xi \xi '$. Let
$\zeta : = \xi \xi '$. Let ![]() $[\xi ] : \mathbb {F}_{p^2} \to \mathcal {O}$ be the Teichmüller lift of
$[\xi ] : \mathbb {F}_{p^2} \to \mathcal {O}$ be the Teichmüller lift of ![]() $\xi$ which will be viewed as a multiplicative character of
$\xi$ which will be viewed as a multiplicative character of ![]() $\mathbb {F}_{p^2}^{\times }$. We have
$\mathbb {F}_{p^2}^{\times }$. We have ![]() $[x]^{p-1} = \mathbf {1}$ and
$[x]^{p-1} = \mathbf {1}$ and ![]() $[\xi ]^{p+1} = [x]$.
$[\xi ]^{p+1} = [x]$.
(i) Let
 $0\leq a \leq p-1$ and
$0\leq a \leq p-1$ and  $0\leq b\leq p-2$. Then
$0\leq b\leq p-2$. Then
 \[ \overline{I([x]^b , [x]^{b+a})}^{\rm ss} \cong \sigma_{a,b} \oplus \sigma_{p-1-a, a+b}. \]
\[ \overline{I([x]^b , [x]^{b+a})}^{\rm ss} \cong \sigma_{a,b} \oplus \sigma_{p-1-a, a+b}. \]
(ii) Let
 $\psi :\mathbb {F}_{p^2}^{\times } \to E^{\times }$ with
$\psi :\mathbb {F}_{p^2}^{\times } \to E^{\times }$ with  $\psi \neq \psi ^p$. Write
$\psi \neq \psi ^p$. Write  $\psi = [\xi ]^{a+1 + (p+1)b}$ with
$\psi = [\xi ]^{a+1 + (p+1)b}$ with  $0\leq a \leq p-1$ and
$0\leq a \leq p-1$ and  $0\leq b\leq p-2$. Then
with the convention that
$0\leq b\leq p-2$. Then
with the convention that \[ \overline{\Theta(\psi)}^{\rm ss} \cong \sigma_{a-1, b+1} \oplus \sigma_{p-2-a, a+b+1}, \]
\[ \overline{\Theta(\psi)}^{\rm ss} \cong \sigma_{a-1, b+1} \oplus \sigma_{p-2-a, a+b+1}, \]
 $\sigma _{-1, b} = 0$.
$\sigma _{-1, b} = 0$.(iii) The representations
 $I([x]^b , [x]^{b+a})$ and
$I([x]^b , [x]^{b+a})$ and  $\Theta (\psi )$ are residually multiplicity free.
$\Theta (\psi )$ are residually multiplicity free.
Proof. Part (i) follows from [Reference DiamondDia07, Proposition 1.1]; part (ii) follows from [Reference DiamondDia07, Proposition 1.3]. Part (iii) follows directly from parts (i) and (ii).
We recall Lemma 4.1.1 of [Reference Emerton, Gee and SavittEGS15] on the lattices of finite-dimensional irreducible residually multiplicity-free ![]() $E$-representations of
$E$-representations of ![]() $K$.
$K$.
Proposition 3.7 [Reference Emerton, Gee and SavittEGS15]
Let ![]() $V$ be a finite-dimensional irreducible representation of
$V$ be a finite-dimensional irreducible representation of ![]() $K$ over
$K$ over ![]() $E$ which is residually multiplicity free. Let
$E$ which is residually multiplicity free. Let ![]() $\sigma$ be a Jordan–Hölder factor of
$\sigma$ be a Jordan–Hölder factor of ![]() $\overline {V}^{\rm ss}$. Then there is up to homothety a unique lattice
$\overline {V}^{\rm ss}$. Then there is up to homothety a unique lattice ![]() $V^{\circ }_{\sigma }$ in
$V^{\circ }_{\sigma }$ in ![]() $V$ such that the socle of
$V$ such that the socle of ![]() $\overline {V^{\circ }_{\sigma }}$ is
$\overline {V^{\circ }_{\sigma }}$ is ![]() $\sigma$. Similarly, there is up to homothety a unique lattice
$\sigma$. Similarly, there is up to homothety a unique lattice ![]() $V^{\circ,\sigma }$ in
$V^{\circ,\sigma }$ in ![]() $V$ such that the cosocle of
$V$ such that the cosocle of ![]() $\overline {V^{\circ,\sigma }}$ is
$\overline {V^{\circ,\sigma }}$ is ![]() $\sigma$.
$\sigma$.
3.3 Lattices in  $ \underline {\mathrm {Sym}}^1E^2 \otimes \Theta (\psi )$
$ \underline {\mathrm {Sym}}^1E^2 \otimes \Theta (\psi )$
Let ![]() $\mathrm {pr}:\mathbb {Q}_p^{\times }\rightarrow 1+p\mathbb {Z}_p$ denote the projection sending
$\mathrm {pr}:\mathbb {Q}_p^{\times }\rightarrow 1+p\mathbb {Z}_p$ denote the projection sending ![]() $p$ to
$p$ to ![]() $1$. As
$1$. As ![]() $p>2$, we can define the square root on
$p>2$, we can define the square root on ![]() $1+p\mathbb {Z}_p$ by the usual binomial formula. Define
$1+p\mathbb {Z}_p$ by the usual binomial formula. Define
The reason to introduce the twist is to make the central character of ![]() $\underline {\mathrm {Sym}}^1E^2$ to be trivial on
$\underline {\mathrm {Sym}}^1E^2$ to be trivial on ![]() $Z_1$. Note that the mod
$Z_1$. Note that the mod ![]() $p$ reduction of
$p$ reduction of ![]() $\underline {\mathrm {Sym}}^1\mathcal {O}^2:=\mathrm {Sym}^{1}\mathcal {O}^2\otimes (\mathrm {pr}\circ \det )^{-1/2}$ still gives
$\underline {\mathrm {Sym}}^1\mathcal {O}^2:=\mathrm {Sym}^{1}\mathcal {O}^2\otimes (\mathrm {pr}\circ \det )^{-1/2}$ still gives ![]() $\mathrm {Sym}^1\mathbb {F}^2$.
$\mathrm {Sym}^1\mathbb {F}^2$.
Let ![]() $\psi : \mathbb {F}_{p^2}^{\times } \to E^{\times }$ be a character with
$\psi : \mathbb {F}_{p^2}^{\times } \to E^{\times }$ be a character with ![]() $\psi \neq \psi ^p$. Write
$\psi \neq \psi ^p$. Write ![]() $\psi = [\xi ]^{a+1 + (p+1)b}$ with
$\psi = [\xi ]^{a+1 + (p+1)b}$ with ![]() $0\leq a \leq p-1$ and
$0\leq a \leq p-1$ and ![]() $0\leq b\leq p-2$. By Proposition 3.6,
$0\leq b\leq p-2$. By Proposition 3.6, ![]() $\overline {\Theta (\psi )}^{\rm ss}$ is multiplicity free and has two (respectively, one) Jordan–Hölder factors if
$\overline {\Theta (\psi )}^{\rm ss}$ is multiplicity free and has two (respectively, one) Jordan–Hölder factors if ![]() $1 \leq a \leq p-2$ (respectively, if
$1 \leq a \leq p-2$ (respectively, if ![]() $a\in \{0,p-1\}$).
$a\in \{0,p-1\}$).
Assume first ![]() $1\leq a\leq p-2$. By Propositions 3.6 and 3.7, there are two lattices
$1\leq a\leq p-2$. By Propositions 3.6 and 3.7, there are two lattices ![]() $T,T'$ in
$T,T'$ in ![]() $\Theta (\psi )$ such that
$\Theta (\psi )$ such that
where both extensions are nonsplit. Note that ![]() $T/pT$ and
$T/pT$ and ![]() $T'/pT'$ are
$T'/pT'$ are ![]() $\Gamma$-representations as
$\Gamma$-representations as ![]() $\Theta (\psi )$ itself is. Moreover, if we fix
$\Theta (\psi )$ itself is. Moreover, if we fix ![]() $T$ and normalize
$T$ and normalize ![]() $T'$ (by a scalar) so that
$T'$ (by a scalar) so that ![]() $T'\subset T$ and
$T'\subset T$ and ![]() $T'\nsubseteq pT$, then by [Reference Emerton, Gee and SavittEGS15, Proposition 5.2.3(1)] we have
$T'\nsubseteq pT$, then by [Reference Emerton, Gee and SavittEGS15, Proposition 5.2.3(1)] we have
(i) We have
 $(T/pT)^{I_1}\cong \chi _{p-2-a,a+b+1}$ and
$(T/pT)^{I_1}\cong \chi _{p-2-a,a+b+1}$ and  $(T'/pT')^{I_1}\cong \chi _{a-1,b+1}$.
$(T'/pT')^{I_1}\cong \chi _{a-1,b+1}$.(ii) We have
 $(T / pT)_{I_1} = \chi ^s_{ a -1, b +1}$ and
$(T / pT)_{I_1} = \chi ^s_{ a -1, b +1}$ and  $(T'/pT')_{I_1}\cong \chi _{p-2-a,a+b+1}^{s}$.
$(T'/pT')_{I_1}\cong \chi _{p-2-a,a+b+1}^{s}$.
Proof. (i) We only give the proof in the case of ![]() $T/pT$. Using (3.3) we obtain an exact sequence
$T/pT$. Using (3.3) we obtain an exact sequence
Assume for a contradiction that ![]() $(T / pT)^{I_1}$ is two-dimensional. Then we would obtain
$(T / pT)^{I_1}$ is two-dimensional. Then we would obtain
and consequently an ![]() $I$-equivariant injection
$I$-equivariant injection ![]() $\chi _{a-1,b+1}\hookrightarrow T/pT$. By Frobenius reciprocity, we would get a nonzero
$\chi _{a-1,b+1}\hookrightarrow T/pT$. By Frobenius reciprocity, we would get a nonzero ![]() $K$-equivariant map
$K$-equivariant map
By comparing the Jordan–Hölder factors, this map cannot be injective and must have image isomorphic to ![]() $\sigma _{a-1,b+1}$ (see [Reference Breuil and PaškūnasBP12, Lemma 2.3]). This gives a contradiction because the sequence (3.3) is nonsplit.
$\sigma _{a-1,b+1}$ (see [Reference Breuil and PaškūnasBP12, Lemma 2.3]). This gives a contradiction because the sequence (3.3) is nonsplit.
(ii) This is proved in a similar way as part (i). Alternatively, it can be deduced from part (i) by taking dual.
Recall that ![]() $E$ is unramified over
$E$ is unramified over ![]() $\mathbb {Q}_p$. Consider
$\mathbb {Q}_p$. Consider ![]() $\underline {\mathrm {Sym}}^1\mathcal {O}^2:=\mathcal {O} Y\oplus \mathcal {O} X$, the standard lattice in
$\underline {\mathrm {Sym}}^1\mathcal {O}^2:=\mathcal {O} Y\oplus \mathcal {O} X$, the standard lattice in ![]() $\underline {\mathrm {Sym}}^1E^2$ and set
$\underline {\mathrm {Sym}}^1E^2$ and set
Then we haveFootnote 2
 \begin{align*} L / p L &\cong \mathrm{Sym}^1\mathbb{F}^2\otimes T/pT,\\ L' / p L' &\cong \mathrm{Sym}^1\mathbb{F}^2\otimes T'/p T', \end{align*}
\begin{align*} L / p L &\cong \mathrm{Sym}^1\mathbb{F}^2\otimes T/pT,\\ L' / p L' &\cong \mathrm{Sym}^1\mathbb{F}^2\otimes T'/p T', \end{align*}
and (3.5) implies ![]() $p L \subset L' \subset L$.
$p L \subset L' \subset L$.
Lemma 3.9 The group ![]() $K_1$ acts trivially on
$K_1$ acts trivially on ![]() $L/pL$ and
$L/pL$ and ![]() $L'/pL'$.
$L'/pL'$.
Proof. This is because ![]() $K_1$ acts trivially on both
$K_1$ acts trivially on both ![]() $\mathrm {Sym}^1\mathbb {F}^2$ and
$\mathrm {Sym}^1\mathbb {F}^2$ and ![]() $\Theta (\psi )$.
$\Theta (\psi )$.
(i) We have
 $(L/pL)^{I_1}\cong \chi _{p-1-a,a+b+1}\oplus \chi _{p-3-a,a+b+2}$ and
$(L/pL)^{I_1}\cong \chi _{p-1-a,a+b+1}\oplus \chi _{p-3-a,a+b+2}$ and  $(L'/pL')^{I_1}\cong \chi _{a,b+1}\oplus \chi _{a-2,b+2}$.
$(L'/pL')^{I_1}\cong \chi _{a,b+1}\oplus \chi _{a-2,b+2}$.(ii) We have
 $(L / p L)_{I_1} \cong \chi ^s_{ a, b +1} \oplus \chi ^s_{ a - 2, b +2}$ and
$(L / p L)_{I_1} \cong \chi ^s_{ a, b +1} \oplus \chi ^s_{ a - 2, b +2}$ and  $(L'/pL')_{I_1}\cong \chi _{p-1-a,a+b+1}^s\oplus \chi _{p-3-a.a+b+2}^s$.
$(L'/pL')_{I_1}\cong \chi _{p-1-a,a+b+1}^s\oplus \chi _{p-3-a.a+b+2}^s$.
Proof. By Lemma 3.9, we have ![]() $(L/pL)^{I_1}=(L/pL)^{U(\mathbb {Z}_p)}$ and
$(L/pL)^{I_1}=(L/pL)^{U(\mathbb {Z}_p)}$ and ![]() $(L/pL)_{I_1}=(L/pL)_{U(\mathbb {Z}_p)}$, so the results follow from Proposition 3.1 and Lemma 3.8.
$(L/pL)_{I_1}=(L/pL)_{U(\mathbb {Z}_p)}$, so the results follow from Proposition 3.1 and Lemma 3.8.
Proposition 3.11 Assume ![]() $1\leq a \leq p-2$.
$1\leq a \leq p-2$.
(i) We have that
 $L/pL$ is multiplicity free and has a two-step socle (and cosocle) filtration
(3.8)(with the convention
$L/pL$ is multiplicity free and has a two-step socle (and cosocle) filtration
(3.8)(with the convention \begin{equation} (\sigma_{p-3-a, a+b+2} \oplus\sigma_{p-1-a, a+b+1}) \ \textbf{---}\ (\sigma_{a, b+1} \oplus \sigma_{a-2, b+2}) \end{equation}
\begin{equation} (\sigma_{p-3-a, a+b+2} \oplus\sigma_{p-1-a, a+b+1}) \ \textbf{---}\ (\sigma_{a, b+1} \oplus \sigma_{a-2, b+2}) \end{equation} $\sigma _{-1,b+1} = \sigma _{-1,b+2} =0$). Moreover, the following nonsplit extensions
occur in
$\sigma _{-1,b+1} = \sigma _{-1,b+2} =0$). Moreover, the following nonsplit extensions
occur in \begin{align*} E_1 &= (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}),\\ E_2 &= (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a-2, b+2}),\\ E_3 &= (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a, b+1}) \end{align*}
\begin{align*} E_1 &= (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}),\\ E_2 &= (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a-2, b+2}),\\ E_3 &= (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a, b+1}) \end{align*}
 $L/pL$ as subquotients, with the exception that
$L/pL$ as subquotients, with the exception that  $E_1$ (respectively,
$E_1$ (respectively,  $E_2$) does not exist if
$E_2$) does not exist if  $a=p-2$ (respectively,
$a=p-2$ (respectively,  $a=1$).
$a=1$).(ii) We have that
 $L'/pL'$ is multiplicity free and has a two-step socle (and cosocle) filtration
(with the convention
$L'/pL'$ is multiplicity free and has a two-step socle (and cosocle) filtration
(with the convention \[ (\sigma_{a, b+1} \oplus \sigma_{a-2, b+2}) \ \textbf{---}\ (\sigma_{p-3-a, a+b+2} \oplus\sigma_{p-1-a, a+b+1}). \]
\[ (\sigma_{a, b+1} \oplus \sigma_{a-2, b+2}) \ \textbf{---}\ (\sigma_{p-3-a, a+b+2} \oplus\sigma_{p-1-a, a+b+1}). \]
 $\sigma _{-1,b+1} = \sigma _{-1,b+2} =0$). Moreover, the following nonsplit extensions
occur in
$\sigma _{-1,b+1} = \sigma _{-1,b+2} =0$). Moreover, the following nonsplit extensions
occur in \begin{align*} E'_1 &= (\sigma_{a, b+1} \ \textbf{---}\ \sigma_{p-3-a, a+b +2}),\\ E'_2 & = ( \sigma_{a-2, b+2} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}),\\ E'_3 & = (\sigma_{a, b+1} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}) \end{align*}
\begin{align*} E'_1 &= (\sigma_{a, b+1} \ \textbf{---}\ \sigma_{p-3-a, a+b +2}),\\ E'_2 & = ( \sigma_{a-2, b+2} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}),\\ E'_3 & = (\sigma_{a, b+1} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}) \end{align*}
 $L'/pL'$ as subquotients, with the exception that
$L'/pL'$ as subquotients, with the exception that  $E'_1$ (respectively,
$E'_1$ (respectively,  $E'_2$) does not exist if
$E'_2$) does not exist if  $a=p-2$ (respectively,
$a=p-2$ (respectively,  $a=1$).
$a=1$).
Proof. It suffices to prove part (i). Recall the following facts (see [Reference Breuil and PaškūnasBP12, Lemma 3.8])
 \begin{align*} \mathrm{Sym}^1\mathbb{F}^2\otimes \sigma_{a-1, b+1} &\cong \sigma_{a, b+1} \oplus \sigma_{a-2, b+2}, \\ \mathrm{Sym}^1\mathbb{F}^2\otimes\sigma_{p-2-a,a+b+1} &\cong \sigma_{p-1-a,a+b+1}\oplus\sigma_{p-3-a,a+b+2}, \end{align*}
\begin{align*} \mathrm{Sym}^1\mathbb{F}^2\otimes \sigma_{a-1, b+1} &\cong \sigma_{a, b+1} \oplus \sigma_{a-2, b+2}, \\ \mathrm{Sym}^1\mathbb{F}^2\otimes\sigma_{p-2-a,a+b+1} &\cong \sigma_{p-1-a,a+b+1}\oplus\sigma_{p-3-a,a+b+2}, \end{align*}
with the convention ![]() $\sigma _{-1,b+1} = \sigma _{-1,b+2}= 0$. Using (3.3) this implies that
$\sigma _{-1,b+1} = \sigma _{-1,b+2}= 0$. Using (3.3) this implies that ![]() $L/pL\cong \mathrm {Sym}^1\mathbb {F}^2\otimes T/pT$ has a two-step filtration as claimed in (3.8), and is multiplicity free. By Lemma 3.10, the filtration gives exactly the socle (and cosocle) filtration. This also completes the proof if
$L/pL\cong \mathrm {Sym}^1\mathbb {F}^2\otimes T/pT$ has a two-step filtration as claimed in (3.8), and is multiplicity free. By Lemma 3.10, the filtration gives exactly the socle (and cosocle) filtration. This also completes the proof if ![]() $a\in \{1,p-2\}$.
$a\in \{1,p-2\}$.
Assume ![]() $2\leq a \leq p-3$ in the rest of the proof. For a Serre weight
$2\leq a \leq p-3$ in the rest of the proof. For a Serre weight ![]() $\sigma$, denote by
$\sigma$, denote by ![]() ${\rm Inj}_{\Gamma }(\sigma )$ the injective envelope of
${\rm Inj}_{\Gamma }(\sigma )$ the injective envelope of ![]() $\sigma$ in the category of
$\sigma$ in the category of ![]() $\mathbb {F}[\Gamma ]$-modules; we remark that
$\mathbb {F}[\Gamma ]$-modules; we remark that ![]() $\mathrm {Inj}_{\Gamma }(\sigma )$ is also projective. Let
$\mathrm {Inj}_{\Gamma }(\sigma )$ is also projective. Let ![]() $W_1$ denote the image of the unique (up to scalar) nonzero map
$W_1$ denote the image of the unique (up to scalar) nonzero map ![]() ${\rm Inj}_{\Gamma }(\sigma _{a-2,b+2}) \to L/ p L$. Since
${\rm Inj}_{\Gamma }(\sigma _{a-2,b+2}) \to L/ p L$. Since ![]() $\sigma _{p-3-a, a+b+2}$ is not a Jordan–Hölder factor of
$\sigma _{p-3-a, a+b+2}$ is not a Jordan–Hölder factor of ![]() ${\rm Inj}_{\Gamma }(\sigma _{a-2,b+2})$ (see [Reference Breuil and PaškūnasBP12, Lemma 3.2]),
${\rm Inj}_{\Gamma }(\sigma _{a-2,b+2})$ (see [Reference Breuil and PaškūnasBP12, Lemma 3.2]), ![]() $W_1$ does not admit
$W_1$ does not admit ![]() $\sigma _{p-3-a,a+b+2}$ as a subquotient. Since
$\sigma _{p-3-a,a+b+2}$ as a subquotient. Since ![]() $\mathrm {cosoc}(W_1)\cong \sigma _{a-2,b+2}$ by construction, we deduce from (3.8) that
$\mathrm {cosoc}(W_1)\cong \sigma _{a-2,b+2}$ by construction, we deduce from (3.8) that
i.e. the nonsplit extension ![]() $E_2$ occurs in
$E_2$ occurs in ![]() $L/pL$. Consequently, the cokernel of the inclusion
$L/pL$. Consequently, the cokernel of the inclusion ![]() $W_1\hookrightarrow L/ p L$, denoted by
$W_1\hookrightarrow L/ p L$, denoted by ![]() $W_2$, has
$W_2$, has ![]() $\{\sigma _{a,b+1},\sigma _{p-3-a,a+b+2}\}$ as the set of Jordan–Hölder factors, hence is isomorphic to the nonsplit extension
$\{\sigma _{a,b+1},\sigma _{p-3-a,a+b+2}\}$ as the set of Jordan–Hölder factors, hence is isomorphic to the nonsplit extension ![]() $E_1=(\sigma _{p- 3-a, a+b+2} \ \textbf {---}\ \sigma _{a , b+1})$ because
$E_1=(\sigma _{p- 3-a, a+b+2} \ \textbf {---}\ \sigma _{a , b+1})$ because ![]() $\sigma _{p-3-a,a+b+2}$ does not occur in the cosocle of
$\sigma _{p-3-a,a+b+2}$ does not occur in the cosocle of ![]() $W_2$ by (3.8).
$W_2$ by (3.8).
We are left to show that ![]() $L / pL$ is a nonsplit extension of
$L / pL$ is a nonsplit extension of ![]() $W_2$ by
$W_2$ by ![]() $W_1$ (this implies that
$W_1$ (this implies that ![]() $E_3$ occurs in
$E_3$ occurs in ![]() $L/pL$). Assume for a contradiction that
$L/pL$). Assume for a contradiction that ![]() $L / pL \cong W_1 \oplus W_2$. Let
$L / pL \cong W_1 \oplus W_2$. Let ![]() $V$ denote the principal series
$V$ denote the principal series ![]() $\operatorname {{\mathrm {Ind}}}_{I}^{K}\chi _{a+1,b}^s$ which is isomorphic to the (unique) nonsplit extension
$\operatorname {{\mathrm {Ind}}}_{I}^{K}\chi _{a+1,b}^s$ which is isomorphic to the (unique) nonsplit extension ![]() $(\sigma _{a+1,b}\ \textbf {---}\ \sigma _{p-2-a,a+b+1})$. By [Reference Breuil and PaškūnasBP12, § 3], there exists a short exact sequence
$(\sigma _{a+1,b}\ \textbf {---}\ \sigma _{p-2-a,a+b+1})$. By [Reference Breuil and PaškūnasBP12, § 3], there exists a short exact sequence
which induces a short exact sequence
By Lemma 3.12 below, if ![]() $2 \leq a \leq p-4$, then
$2 \leq a \leq p-4$, then
Comparing the socles, it is clear that ![]() $W_2\cap {\rm Inj}_{\Gamma } (\sigma _{p -1-a, a+b+1})\,{=}\,0$, thus
$W_2\cap {\rm Inj}_{\Gamma } (\sigma _{p -1-a, a+b+1})\,{=}\,0$, thus ![]() $W_2\!\hookrightarrow\! {\rm Inj}_{\Gamma } (\sigma _{p-3-a,a+b+2})$. Moreover, we have
$W_2\!\hookrightarrow\! {\rm Inj}_{\Gamma } (\sigma _{p-3-a,a+b+2})$. Moreover, we have
which induces a (nonzero) morphism
However, by [Reference Breuil and PaškūnasBP12, § 3] we have
so by Frobenius reciprocity we obtain a nonzero ![]() $I$-equivariant morphism
$I$-equivariant morphism
But this contradicts Corollary 3.2, by which ![]() $(\mathrm {Sym}^{1}\mathbb {F}^2\otimes V)^{I_1}\cong \chi _{a+2,b}\oplus \chi _{a,b+1}\oplus \chi _{p-1-a,a+b+1}$.
$(\mathrm {Sym}^{1}\mathbb {F}^2\otimes V)^{I_1}\cong \chi _{a+2,b}\oplus \chi _{a,b+1}\oplus \chi _{p-1-a,a+b+1}$.
The case ![]() $a = p-3$ is a little subtle. By Lemma 3.12 below we have
$a = p-3$ is a little subtle. By Lemma 3.12 below we have
Comparing the socles, one checks that ![]() $W_2$ embeds into
$W_2$ embeds into ![]() ${\rm Inj}_{\Gamma } (\sigma _{0,b})$ and actually
${\rm Inj}_{\Gamma } (\sigma _{0,b})$ and actually
Hence, we obtain a nonzero morphism from ![]() ${\rm Inj}_{\Gamma } (\sigma _{0,b})/ W_2 \cong \sigma _{0,b}$ to
${\rm Inj}_{\Gamma } (\sigma _{0,b})/ W_2 \cong \sigma _{0,b}$ to ![]() $\mathrm {Sym}^1\mathbb {F}^2 \otimes V$. On the other hand,
$\mathrm {Sym}^1\mathbb {F}^2 \otimes V$. On the other hand, ![]() $\sigma _{p-1,b}$ also occurs in
$\sigma _{p-1,b}$ also occurs in ![]() $\mathrm {Sym}^1\mathbb {F}^2\otimes V$ and, in fact, is a direct summand because
$\mathrm {Sym}^1\mathbb {F}^2\otimes V$ and, in fact, is a direct summand because ![]() $\sigma _{p-1,b}$ is an injective
$\sigma _{p-1,b}$ is an injective ![]() $\mathbb {F}[\Gamma ]$-module. Thus, there exists an embedding
$\mathbb {F}[\Gamma ]$-module. Thus, there exists an embedding
However, by Corollary 3.2 we have ![]() $(\mathrm {Sym}^{1}\mathbb {F}^2\otimes V)^{I_1}\cong \chi _{p-1,b}\oplus \chi _{p-3,b+1}\oplus \chi _{2,b-1}$, in which the character
$(\mathrm {Sym}^{1}\mathbb {F}^2\otimes V)^{I_1}\cong \chi _{p-1,b}\oplus \chi _{p-3,b+1}\oplus \chi _{2,b-1}$, in which the character ![]() $\chi _{p-1,b}$ (
$\chi _{p-1,b}$ (![]() $=\chi _{0,b}$) occurs only once. This gives a contradiction and finishes the proof.
$=\chi _{0,b}$) occurs only once. This gives a contradiction and finishes the proof.
Recall the following facts (see [Reference Breuil and PaškūnasBP12, § 3]): ![]() ${\rm Inj}_{\Gamma } (\sigma _{a , b})$ is of dimension
${\rm Inj}_{\Gamma } (\sigma _{a , b})$ is of dimension ![]() $2p$ if
$2p$ if ![]() $1\leq a \leq p-2$;
$1\leq a \leq p-2$; ![]() ${\rm Inj}_{\Gamma }(\sigma _{p-1,b}) \cong \sigma _{p-1 , b}$ is of dimension
${\rm Inj}_{\Gamma }(\sigma _{p-1,b}) \cong \sigma _{p-1 , b}$ is of dimension ![]() $p$;
$p$; ![]() ${\rm Inj}_{\Gamma } (\sigma _{0,b}) \cong (\sigma _{0,b} \ \textbf {---}\ \sigma _{p-3, b+1} \ \textbf {---}\ \sigma _{0,b})$ is of dimension
${\rm Inj}_{\Gamma } (\sigma _{0,b}) \cong (\sigma _{0,b} \ \textbf {---}\ \sigma _{p-3, b+1} \ \textbf {---}\ \sigma _{0,b})$ is of dimension ![]() $p$.
$p$.
(i) If
 $a = 1$, then
$a = 1$, then  $\mathrm {Sym}^1 \mathbb {F}^2 \otimes {\rm Inj}_{\Gamma } (\sigma _{1, b}) \cong {\rm Inj}_{\Gamma } (\sigma _{2, b})\oplus {\rm Inj}_{\Gamma }(\sigma _{0, b+1}) \oplus \sigma _{p-1, b+1}$.
$\mathrm {Sym}^1 \mathbb {F}^2 \otimes {\rm Inj}_{\Gamma } (\sigma _{1, b}) \cong {\rm Inj}_{\Gamma } (\sigma _{2, b})\oplus {\rm Inj}_{\Gamma }(\sigma _{0, b+1}) \oplus \sigma _{p-1, b+1}$.(ii) If
 $a = p-2$, then
$a = p-2$, then  $\mathrm {Sym}^1 \mathbb {F}^2 \otimes {\rm Inj}_{\Gamma } (\sigma _{p-2, b}) \cong \sigma _{p-1, b}\oplus \sigma _{p-1, b} \oplus {\rm Inj}_{\Gamma }(\sigma _{p-3, b+1})$.
$\mathrm {Sym}^1 \mathbb {F}^2 \otimes {\rm Inj}_{\Gamma } (\sigma _{p-2, b}) \cong \sigma _{p-1, b}\oplus \sigma _{p-1, b} \oplus {\rm Inj}_{\Gamma }(\sigma _{p-3, b+1})$.(iii) If
 $0 \leq a \leq p - 1$ and
$0 \leq a \leq p - 1$ and  $a\notin \{1,p-2\}$, then
$a\notin \{1,p-2\}$, then  $\mathrm {Sym}^1 \mathbb {F}^2 \otimes {\rm Inj}_{\Gamma } (\sigma _{a, b}) \!=\! {\rm Inj}_{\Gamma } (\sigma _{a+1, b})\oplus {\rm Inj}_{\Gamma }(\sigma _{a - 1, b+1})$ with the convention
$\mathrm {Sym}^1 \mathbb {F}^2 \otimes {\rm Inj}_{\Gamma } (\sigma _{a, b}) \!=\! {\rm Inj}_{\Gamma } (\sigma _{a+1, b})\oplus {\rm Inj}_{\Gamma }(\sigma _{a - 1, b+1})$ with the convention  ${\rm Inj}_{\Gamma }(\sigma _{- 1, b+1}) = {\rm Inj}_{\Gamma }(\sigma _{p, b}) =0$.
${\rm Inj}_{\Gamma }(\sigma _{- 1, b+1}) = {\rm Inj}_{\Gamma }(\sigma _{p, b}) =0$.
Proof. Using the fact that ![]() $\mathrm {Sym}^{1}\mathbb {F}^2\otimes {\rm Inj}_{\Gamma }\sigma$ is an injective object in the category of
$\mathrm {Sym}^{1}\mathbb {F}^2\otimes {\rm Inj}_{\Gamma }\sigma$ is an injective object in the category of ![]() $\mathbb {F}[\Gamma ]$-modules, the results can be easily deduced from [Reference Breuil and PaškūnasBP12, Lemma 3.8].
$\mathbb {F}[\Gamma ]$-modules, the results can be easily deduced from [Reference Breuil and PaškūnasBP12, Lemma 3.8].
Finally, we treat the case ![]() $a\in \{0,p-1\}$.
$a\in \{0,p-1\}$.
Proposition 3.13 Assume ![]() $a\in \{0,p-1\}$. There are two lattices (unique up to homothety)
$a\in \{0,p-1\}$. There are two lattices (unique up to homothety) ![]() $L, L'$ of
$L, L'$ of ![]() $\underline {\mathrm {Sym}}^1 E^2\otimes \Theta (\psi )$ such that
$\underline {\mathrm {Sym}}^1 E^2\otimes \Theta (\psi )$ such that ![]() $pL \subset L' \subset L$ and
$pL \subset L' \subset L$ and
The lattice ![]() $pL$ is then identified with the kernel of the natural projection
$pL$ is then identified with the kernel of the natural projection ![]() $L' \twoheadrightarrow \sigma _{p-3,b+2}$. Moreover,
$L' \twoheadrightarrow \sigma _{p-3,b+2}$. Moreover, ![]() $(L'/pL')_{K_1} \cong \sigma _{p-3, b+2}$.
$(L'/pL')_{K_1} \cong \sigma _{p-3, b+2}$.
Proof. Let ![]() $T$ be any lattice in
$T$ be any lattice in ![]() $\Theta (\psi )$ and
$\Theta (\psi )$ and ![]() $L: = \underline {\mathrm {Sym}}^1 \mathcal {O}^2 \otimes T$. Then
$L: = \underline {\mathrm {Sym}}^1 \mathcal {O}^2 \otimes T$. Then ![]() $T/pT \cong \sigma _{p-2, b+1}$ by Proposition 3.6, and consequently
$T/pT \cong \sigma _{p-2, b+1}$ by Proposition 3.6, and consequently ![]() $L/pL \cong \sigma _{p-1, b+1} \oplus \sigma _{p-3,b+2}$ by [Reference Breuil and PaškūnasBP12, Lemma 3.8]. Let
$L/pL \cong \sigma _{p-1, b+1} \oplus \sigma _{p-3,b+2}$ by [Reference Breuil and PaškūnasBP12, Lemma 3.8]. Let ![]() $L'$ be the kernel of the composition
$L'$ be the kernel of the composition ![]() $L \to L/pL \overset {p_1}{\twoheadrightarrow } \sigma _{p-1,b+1}$. Then
$L \to L/pL \overset {p_1}{\twoheadrightarrow } \sigma _{p-1,b+1}$. Then ![]() $pL \subsetneq L'\subsetneq L$. Moreover, we have a short exact sequence
$pL \subsetneq L'\subsetneq L$. Moreover, we have a short exact sequence
We claim that (3.9) induces an isomorphism ![]() $(L'/pL')_{K_1} \xrightarrow {\sim } \sigma _{p-3,b+2};$ this will imply that
$(L'/pL')_{K_1} \xrightarrow {\sim } \sigma _{p-3,b+2};$ this will imply that ![]() $L'/pL'$ is a nonsplit extension of
$L'/pL'$ is a nonsplit extension of ![]() $\sigma _{p-3,b+2}$ by
$\sigma _{p-3,b+2}$ by ![]() $\sigma _{p-1,b+1}$.
$\sigma _{p-1,b+1}$.
The proof of Proposition 3.1 shows that there exist ![]() $\overline {w}_0,\overline {w}_1\in T/pT$ such that
$\overline {w}_0,\overline {w}_1\in T/pT$ such that ![]() $X\otimes \overline {w}_0$ and
$X\otimes \overline {w}_0$ and ![]() $Y\otimes \overline {w}_0+X\otimes \overline {w}_1$ span
$Y\otimes \overline {w}_0+X\otimes \overline {w}_1$ span ![]() $(L/pL)^{I_1}$. Comparing the
$(L/pL)^{I_1}$. Comparing the ![]() $H$-action, we must have
$H$-action, we must have
Let ![]() $w_0,w_1 \in T$ be a lift of
$w_0,w_1 \in T$ be a lift of ![]() $\overline {w}_0,\overline {w}_1$, respectively. From the definition of
$\overline {w}_0,\overline {w}_1$, respectively. From the definition of ![]() $L'$ we see that
$L'$ we see that ![]() $Y\otimes w_0+X\otimes w_1\in L'$. As
$Y\otimes w_0+X\otimes w_1\in L'$. As ![]() $K_1$ acts trivially on
$K_1$ acts trivially on ![]() $T$, we have
$T$, we have
Since ![]() $(pX )\otimes \overline {w}_0$ generates
$(pX )\otimes \overline {w}_0$ generates ![]() $pL/pL'$, the claim follows.
$pL/pL'$, the claim follows.
The uniqueness of ![]() $L'$ (up to homothety) follows from Proposition 3.7. Since
$L'$ (up to homothety) follows from Proposition 3.7. Since ![]() $pL$ is identified with the kernel of the natural projection
$pL$ is identified with the kernel of the natural projection ![]() $L' \twoheadrightarrow \sigma _{p-3,b+2}$, the uniqueness of
$L' \twoheadrightarrow \sigma _{p-3,b+2}$, the uniqueness of ![]() $L$ follows.
$L$ follows.
3.3.1 Sublattices in  $L$
$L$
In this subsection we specify some sublattices in ![]() $L$ in the case
$L$ in the case ![]() $1 \leq a \leq p-2$. Recall that
$1 \leq a \leq p-2$. Recall that ![]() $\sigma _{-1, b+1} = \sigma _{-1, b+2} = 0$ by our convention.
$\sigma _{-1, b+1} = \sigma _{-1, b+2} = 0$ by our convention.
Let ![]() $L_1 : = \operatorname {{\mathrm {Ker}}}( L \twoheadrightarrow L/p L \twoheadrightarrow \sigma _{a-2, b+2} )$. It is clear that
$L_1 : = \operatorname {{\mathrm {Ker}}}( L \twoheadrightarrow L/p L \twoheadrightarrow \sigma _{a-2, b+2} )$. It is clear that ![]() $pL\subset L_1\subset L$.
$pL\subset L_1\subset L$.
Proposition 3.14 The following nonsplit extensions
 \begin{align*} & (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}),\\ & (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a, b+1}),\\ & (\sigma_{a-2, b+2} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}) \end{align*}
\begin{align*} & (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}),\\ & (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a, b+1}),\\ & (\sigma_{a-2, b+2} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}) \end{align*}
occur in ![]() $L_1/ p L_1$ as subquotients. Consequently,
$L_1/ p L_1$ as subquotients. Consequently, ![]() $L_1/pL_1$ has a cosocle filtration
$L_1/pL_1$ has a cosocle filtration
and ![]() $L_1$ is the unique (up to homothety) lattice in
$L_1$ is the unique (up to homothety) lattice in ![]() $\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi )$ whose reduction has cosocle
$\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi )$ whose reduction has cosocle ![]() $\sigma _{a, b+1}$. Moreover, we have
$\sigma _{a, b+1}$. Moreover, we have
Proof. By construction, we have ![]() $pL\subset L_1$ and
$pL\subset L_1$ and ![]() $L_1 / pL = \operatorname {{\mathrm {Ker}}} (L/pL \to \sigma _{a-2, b+2})$. By Proposition 3.11(i), the cosocle filtration of
$L_1 / pL = \operatorname {{\mathrm {Ker}}} (L/pL \to \sigma _{a-2, b+2})$. By Proposition 3.11(i), the cosocle filtration of ![]() $L_1/pL$ is
$L_1/pL$ is
thus the nonsplit extensions ![]() $(\sigma _{p-3-a, a+b +2} \ \textbf {---}\ \sigma _{a, b+1})$ and
$(\sigma _{p-3-a, a+b +2} \ \textbf {---}\ \sigma _{a, b+1})$ and ![]() $(\sigma _{p-1-a, a+b+1} \ \textbf {---}\ \sigma _{a, b+1})$ occur in
$(\sigma _{p-1-a, a+b+1} \ \textbf {---}\ \sigma _{a, b+1})$ occur in ![]() $L_1/pL$, hence also in
$L_1/pL$, hence also in ![]() $L_1/pL_1$.
$L_1/pL_1$.
We need to show that the nonsplit extension ![]() $(\sigma _{a-2, b+2} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ also occurs in
$(\sigma _{a-2, b+2} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ also occurs in ![]() $L_1/pL_1$. For this we note that
$L_1/pL_1$. For this we note that ![]() $pL_1 \subset L' \subset L_1$, where
$pL_1 \subset L' \subset L_1$, where ![]() $L'$ is defined in (3.7). Consequently,
$L'$ is defined in (3.7). Consequently, ![]() $L' / pL_1$ is a subrepresentation of
$L' / pL_1$ is a subrepresentation of ![]() $L_1 / pL_1$, and it is easy to see that
$L_1 / pL_1$, and it is easy to see that
As a quotient of ![]() $L' / pL'$,
$L' / pL'$, ![]() $L' / pL_1$ admits the nonsplit extension
$L' / pL_1$ admits the nonsplit extension ![]() $(\sigma _{a-2, b+2} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ as a subquotient, see Proposition 3.11(ii). The structure of
$(\sigma _{a-2, b+2} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ as a subquotient, see Proposition 3.11(ii). The structure of ![]() $(L_1 / pL_1)_{K_1}$ and other statements easily follow.
$(L_1 / pL_1)_{K_1}$ and other statements easily follow.
Let ![]() $L_1':=\operatorname {{\mathrm {Ker}}}(L'\twoheadrightarrow L'/pL'\twoheadrightarrow \sigma _{p-3-a,a+b+2})$, where
$L_1':=\operatorname {{\mathrm {Ker}}}(L'\twoheadrightarrow L'/pL'\twoheadrightarrow \sigma _{p-3-a,a+b+2})$, where ![]() $L'$ is defined in (3.7). Then
$L'$ is defined in (3.7). Then ![]() $pL'\subset L_1'\subset L'$. Alternatively,
$pL'\subset L_1'\subset L'$. Alternatively, ![]() $L_1'$ is characterized by the following exact sequence:
$L_1'$ is characterized by the following exact sequence:
In a similar way to Proposition 3.14, we have the following result.
Proposition 3.15 The nonsplit extensions
 \begin{align*} & (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}), \\ & (\sigma_{a, b+1} \ \textbf{---}\ \sigma_{p-1-a, a+b+1} ), \\ & (\sigma_{a-2, b+2} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}) \end{align*}
\begin{align*} & (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}), \\ & (\sigma_{a, b+1} \ \textbf{---}\ \sigma_{p-1-a, a+b+1} ), \\ & (\sigma_{a-2, b+2} \ \textbf{---}\ \sigma_{p-1-a, a+b+1}) \end{align*}
occur in ![]() $L'_1/ p L'_1$. Consequently,
$L'_1/ p L'_1$. Consequently, ![]() $L'_1/pL'_1$ has a cosocle filtration
$L'_1/pL'_1$ has a cosocle filtration
and ![]() $L_1'$ is the unique (up to homothety) lattice in
$L_1'$ is the unique (up to homothety) lattice in ![]() $\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi )$ whose reduction has cosocle
$\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi )$ whose reduction has cosocle ![]() $\sigma _{p-1-a, a+b+1}$. Moreover, we have
$\sigma _{p-1-a, a+b+1}$. Moreover, we have
Let ![]() $L_2 : = \operatorname {{\mathrm {Ker}}}( L \twoheadrightarrow L/p L \twoheadrightarrow (\sigma _{p-3-a, a+b+2} \ \textbf {---}\ \sigma _{a, b+1}) )$. Then
$L_2 : = \operatorname {{\mathrm {Ker}}}( L \twoheadrightarrow L/p L \twoheadrightarrow (\sigma _{p-3-a, a+b+2} \ \textbf {---}\ \sigma _{a, b+1}) )$. Then ![]() $pL\subset L_2\subset L$ and there is a short exact sequence
$pL\subset L_2\subset L$ and there is a short exact sequence
Proposition 3.16 Assume ![]() $2\leq a \leq p-2$. Then the nonsplit extensions
$2\leq a \leq p-2$. Then the nonsplit extensions
 \begin{align*} & (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}),\\ & (\sigma_{a,b+1} \ \textbf{---}\ \sigma_{p-1-a, a+b+1} ),\\ & (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a-2, b+2}) \end{align*}
\begin{align*} & (\sigma_{p-3-a, a+b +2} \ \textbf{---}\ \sigma_{a, b+1}),\\ & (\sigma_{a,b+1} \ \textbf{---}\ \sigma_{p-1-a, a+b+1} ),\\ & (\sigma_{p-1-a, a+b+1} \ \textbf{---}\ \sigma_{a-2, b+2}) \end{align*}
occur in ![]() $L_2/ p L_2$. Consequently,
$L_2/ p L_2$. Consequently, ![]() $L_2/pL_2$ has a cosocle filtration
$L_2/pL_2$ has a cosocle filtration
and ![]() $L_2$ is the unique (up to homothety) lattice in
$L_2$ is the unique (up to homothety) lattice in ![]() $\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi )$ whose reduction has cosocle
$\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi )$ whose reduction has cosocle ![]() $\sigma _{a-2, b+2}$. Moreover, we have
$\sigma _{a-2, b+2}$. Moreover, we have
Proof. Since ![]() $L_2 / pL_2$ is an extension of
$L_2 / pL_2$ is an extension of ![]() $L_2 / pL$ by
$L_2 / pL$ by ![]() $pL / pL_2$, it suffices to show that the nonsplit extension
$pL / pL_2$, it suffices to show that the nonsplit extension ![]() $(\sigma _{a, b+1} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ occurs in
$(\sigma _{a, b+1} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ occurs in ![]() $L_2 / pL_2$.
$L_2 / pL_2$.
It follows from (3.10) and (3.11) that ![]() $pL\subset L'_1\subset L_2$ and there is a short exact sequence
$pL\subset L'_1\subset L_2$ and there is a short exact sequence
This implies that
and the nonsplit extension ![]() $(\sigma _{a, b+1} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ occurs in
$(\sigma _{a, b+1} \ \textbf {---}\ \sigma _{p-1-a, a+b+1})$ occurs in ![]() $L'_1 / pL_2$ by Proposition 3.15. Since
$L'_1 / pL_2$ by Proposition 3.15. Since ![]() $L_1'/pL_2$ embeds in
$L_1'/pL_2$ embeds in ![]() $L_2/pL_2$, this nonsplit extension also occurs in
$L_2/pL_2$, this nonsplit extension also occurs in ![]() $L_2/pL_2$.
$L_2/pL_2$.
The sublattices ![]() $L_1$ and
$L_1$ and ![]() $L_2$ of
$L_2$ of ![]() $L$ satisfy the following property.
$L$ satisfy the following property.
Proposition 3.17 Assume ![]() $3\leq a\leq p-2$. Fix
$3\leq a\leq p-2$. Fix ![]() $i\in \{1,2\}$. Then for every
$i\in \{1,2\}$. Then for every ![]() $x\in p L$, there exist
$x\in p L$, there exist ![]() $r\in \mathbb {N}$,
$r\in \mathbb {N}$, ![]() $k_1,\ldots, k_r \in K_1$,
$k_1,\ldots, k_r \in K_1$, ![]() $y_1,\ldots, y_r \in L_i$, such that
$y_1,\ldots, y_r \in L_i$, such that
The proof of Proposition 3.17 requires a technique introduced in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 7], so we first recall some notation. Let ![]() $\frak {sl}_{2,\mathbb {F}_p}$ be the Lie algebra consisting of trace-zero
$\frak {sl}_{2,\mathbb {F}_p}$ be the Lie algebra consisting of trace-zero ![]() $2\times 2$ matrices with coefficients in
$2\times 2$ matrices with coefficients in ![]() $\mathbb {F}_p$. It is a three-dimensional vector space over
$\mathbb {F}_p$. It is a three-dimensional vector space over ![]() $\mathbb {F}_p$ with a basis
$\mathbb {F}_p$ with a basis
subject to the Lie bracket relations
Let ![]() $(V,\rho )$ be a continuous finite-dimensional representation of
$(V,\rho )$ be a continuous finite-dimensional representation of ![]() $K/Z_1$ over
$K/Z_1$ over ![]() $E$. Assume that
$E$. Assume that ![]() $V^{\circ }$ is a
$V^{\circ }$ is a ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $V$ such that
$V$ such that ![]() $K_1$ acts trivially on
$K_1$ acts trivially on ![]() $V^{\circ } / p V^{\circ }$. Breuil et al. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 7.1] defined a Lie algebra action of
$V^{\circ } / p V^{\circ }$. Breuil et al. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 7.1] defined a Lie algebra action of ![]() $\frak {sl}_{2,\mathbb {F}_p}$ on
$\frak {sl}_{2,\mathbb {F}_p}$ on ![]() $V^{\circ }/pV^{\circ }$, which induces an
$V^{\circ }/pV^{\circ }$, which induces an ![]() $\mathbb {F}$-linear map
$\mathbb {F}$-linear map
sending ![]() $x \otimes v$ to
$x \otimes v$ to ![]() $p^{-1} (\rho (\exp (p \widetilde {x})) \widetilde {v} - \widetilde {v}) \pmod {p V^{\circ }}$, where
$p^{-1} (\rho (\exp (p \widetilde {x})) \widetilde {v} - \widetilde {v}) \pmod {p V^{\circ }}$, where ![]() $\widetilde {x} \in \frak {sl}_{2,\mathbb {Z}_p}$ is a trace-zero
$\widetilde {x} \in \frak {sl}_{2,\mathbb {Z}_p}$ is a trace-zero ![]() $2\times 2$ matrix with coefficients in
$2\times 2$ matrix with coefficients in ![]() $\mathbb {Z}_p$ lifting
$\mathbb {Z}_p$ lifting ![]() $x\in \frak {sl}_{2,\mathbb {F}_p}$, and
$x\in \frak {sl}_{2,\mathbb {F}_p}$, and ![]() $\widetilde {v} \in V^{\circ }$ is a lift of
$\widetilde {v} \in V^{\circ }$ is a lift of ![]() $v \in V^{\circ }/pV^{\circ }$. The definition does not depend on the choice of the lifts. Moreover, letting
$v \in V^{\circ }/pV^{\circ }$. The definition does not depend on the choice of the lifts. Moreover, letting ![]() $K$ act on
$K$ act on ![]() $\frak {sl}_{2,\mathbb {F}_p}$ by conjugation
$\frak {sl}_{2,\mathbb {F}_p}$ by conjugation ![]() $k\cdot x:=\overline {k}x\overline {k}^{-1}$ (for
$k\cdot x:=\overline {k}x\overline {k}^{-1}$ (for ![]() $k\in K$ and
$k\in K$ and ![]() $k\mapsto \overline {k}\in \mathrm {GL}_2(\mathbb {F}_p)$),
$k\mapsto \overline {k}\in \mathrm {GL}_2(\mathbb {F}_p)$), ![]() $\beta _{V^{\circ }}$ is
$\beta _{V^{\circ }}$ is ![]() $K$-equivariant. Indeed,
$K$-equivariant. Indeed,
 \begin{align*} \beta_{V^{\circ}}(k(x\otimes v))=\beta_{V^{\circ}} (\overline{k}x\overline{k}^{-1}\otimes kv) &= p^{-1} (\rho(\exp(pk\widetilde{x}k^{-1}))k\widetilde{v}-k\widetilde{v}) \pmod{p V^{\circ}}\\ &=p^{-1}(\rho(k\exp(p\widetilde{x}))\widetilde{v}-k\widetilde{v})\pmod{p V^{\circ}}\\ &=k\beta_{V^{\circ}}(x\otimes v). \end{align*}
\begin{align*} \beta_{V^{\circ}}(k(x\otimes v))=\beta_{V^{\circ}} (\overline{k}x\overline{k}^{-1}\otimes kv) &= p^{-1} (\rho(\exp(pk\widetilde{x}k^{-1}))k\widetilde{v}-k\widetilde{v}) \pmod{p V^{\circ}}\\ &=p^{-1}(\rho(k\exp(p\widetilde{x}))\widetilde{v}-k\widetilde{v})\pmod{p V^{\circ}}\\ &=k\beta_{V^{\circ}}(x\otimes v). \end{align*}
In the special case ![]() $V=\underline {\mathrm {Sym}}^1E^2$ and
$V=\underline {\mathrm {Sym}}^1E^2$ and ![]() $V^{\circ }=\underline {\mathrm {Sym}}^1\mathcal {O}^2$, we easily check that the map
$V^{\circ }=\underline {\mathrm {Sym}}^1\mathcal {O}^2$, we easily check that the map ![]() $\beta _{\underline {\mathrm {Sym}}^1\mathcal {O}^2}:\frak {sl}_{2,\mathbb {F}_p}\otimes \mathrm {Sym}^1\mathbb {F}^2\rightarrow \mathrm {Sym}^2\mathbb {F}^2$ is given by
$\beta _{\underline {\mathrm {Sym}}^1\mathcal {O}^2}:\frak {sl}_{2,\mathbb {F}_p}\otimes \mathrm {Sym}^1\mathbb {F}^2\rightarrow \mathrm {Sym}^2\mathbb {F}^2$ is given by
for ![]() $\alpha = \big (\begin{smallmatrix} a_{11} & a_{12} \\ a_{21} & -a_{11} \end{smallmatrix}\big ) \in \frak {sl}_{2,\mathbb {F}_p}$ and
$\alpha = \big (\begin{smallmatrix} a_{11} & a_{12} \\ a_{21} & -a_{11} \end{smallmatrix}\big ) \in \frak {sl}_{2,\mathbb {F}_p}$ and ![]() $\ell (X,Y) \in \mathrm {Sym}^1 \mathbb {F}^2$.
$\ell (X,Y) \in \mathrm {Sym}^1 \mathbb {F}^2$.
Proof of Proposition 3.17 We only give the proof for ![]() $L_2$ (which will be used in the proof of Proposition 3.19). Take
$L_2$ (which will be used in the proof of Proposition 3.19). Take ![]() $V=\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi )$ and
$V=\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi )$ and ![]() $V^{\circ }=L=\underline {\mathrm {Sym}}^1\mathcal {O}^2\otimes T$ in the above discussion. Since
$V^{\circ }=L=\underline {\mathrm {Sym}}^1\mathcal {O}^2\otimes T$ in the above discussion. Since ![]() $K_1$ acts trivially on
$K_1$ acts trivially on ![]() $T$, the map
$T$, the map ![]() $\beta _{L}:\frak {sl}_{2,\mathbb {F}_p}\otimes \mathrm {Sym}^1\mathbb {F}^2\otimes T/pT\rightarrow \mathrm {Sym}^1\mathbb {F}^2\otimes T/pT$ is given by (cf. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Remark 7.1.3])
$\beta _{L}:\frak {sl}_{2,\mathbb {F}_p}\otimes \mathrm {Sym}^1\mathbb {F}^2\otimes T/pT\rightarrow \mathrm {Sym}^1\mathbb {F}^2\otimes T/pT$ is given by (cf. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Remark 7.1.3])
Let ![]() $W_1=(\sigma _{p - 1-a, a+b+1} \ \textbf {---}\ \sigma _{a-2, b+2})$ be the subrepresentation of
$W_1=(\sigma _{p - 1-a, a+b+1} \ \textbf {---}\ \sigma _{a-2, b+2})$ be the subrepresentation of ![]() $L/ pL$ defined in the proof of Proposition 3.11. Then
$L/ pL$ defined in the proof of Proposition 3.11. Then ![]() $L_2$ is exactly the preimage of
$L_2$ is exactly the preimage of ![]() $W_1$ in
$W_1$ in ![]() $L$ under the surjection
$L$ under the surjection ![]() $L \twoheadrightarrow L/pL$. Taking
$L \twoheadrightarrow L/pL$. Taking ![]() $W= W_1$ (and
$W= W_1$ (and ![]() $V^\circ = L$) in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Lemma 7.1.4], we obtain the following commutative diagram in which both rows are exact.
$V^\circ = L$) in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Lemma 7.1.4], we obtain the following commutative diagram in which both rows are exact.

To prove the proposition, it suffices to check that the dotted map ![]() $\varphi$, which is the composite
$\varphi$, which is the composite
is surjective, since this implies that the images of ![]() $pL$ and
$pL$ and ![]() $p^2L$ in
$p^2L$ in ![]() $(L_2)_{K_1}$ coincide. Recall that
$(L_2)_{K_1}$ coincide. Recall that ![]() $T/pT$ fits into a short exact sequence
$T/pT$ fits into a short exact sequence
and ![]() $W_1\cap (\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{p-2-a,a+b+1})=\sigma _{p-1-a,a+b+1}$ (see the proof of Proposition 3.11). Using (3.13), we see that
$W_1\cap (\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{p-2-a,a+b+1})=\sigma _{p-1-a,a+b+1}$ (see the proof of Proposition 3.11). Using (3.13), we see that ![]() $\varphi$ sends
$\varphi$ sends ![]() $\frak {sl}_{2,\mathbb {F}_p}\otimes \sigma _{p-1-a,a+b+1}$ to
$\frak {sl}_{2,\mathbb {F}_p}\otimes \sigma _{p-1-a,a+b+1}$ to ![]() $\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{p-2-a,a+b+1}$, so that
$\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{p-2-a,a+b+1}$, so that ![]() $\varphi$ induces a
$\varphi$ induces a ![]() $K$-equivariant map
$K$-equivariant map
where the second map is given by ![]() $\beta _{\underline {\mathrm {Sym}}^1\mathcal {O}^2}\otimes \mathrm {Id}_{\sigma _{a-1,b+1}}$. By Proposition 3.11(i),
$\beta _{\underline {\mathrm {Sym}}^1\mathcal {O}^2}\otimes \mathrm {Id}_{\sigma _{a-1,b+1}}$. By Proposition 3.11(i), ![]() $\mathrm {cosoc}(L/pL)=\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}$. Hence, to prove
$\mathrm {cosoc}(L/pL)=\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}$. Hence, to prove ![]() $\varphi$ is surjective it suffices to prove
$\varphi$ is surjective it suffices to prove ![]() $\overline {\varphi }$ is surjective.
$\overline {\varphi }$ is surjective.
We prove that ![]() $\overline {\varphi }$ is surjective by a direct computation (analogous to [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Lemma 7.2.1]). Fix a nonzero element
$\overline {\varphi }$ is surjective by a direct computation (analogous to [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Lemma 7.2.1]). Fix a nonzero element ![]() $v\in (\sigma _{a-1,b+1})^{U(\mathbb {Z}_p)}$. Then
$v\in (\sigma _{a-1,b+1})^{U(\mathbb {Z}_p)}$. Then ![]() $(\sigma _{a-1,b+1})^{U(\mathbb {Z}_p)} = \mathbb {F} v$ and the group
$(\sigma _{a-1,b+1})^{U(\mathbb {Z}_p)} = \mathbb {F} v$ and the group ![]() $H = \{\big (\begin{smallmatrix} {[a]} & {0}\\ {0} & {[d]}\end{smallmatrix}\big ),\ a,d\in \mathbb {F}_p^{\times }\}$ acts on
$H = \{\big (\begin{smallmatrix} {[a]} & {0}\\ {0} & {[d]}\end{smallmatrix}\big ),\ a,d\in \mathbb {F}_p^{\times }\}$ acts on ![]() $v$ by
$v$ by ![]() $\chi _{a-1,b+1}$. Recall that there is a natural action of
$\chi _{a-1,b+1}$. Recall that there is a natural action of ![]() $\frak {sl}_{2,\mathbb {F}_p}$ on
$\frak {sl}_{2,\mathbb {F}_p}$ on ![]() $\sigma _{a-1,b+1}$ and the set
$\sigma _{a-1,b+1}$ and the set ![]() $\{v,f(v),\ldots, f^{a-1}(v)\}$ forms an
$\{v,f(v),\ldots, f^{a-1}(v)\}$ forms an ![]() $\mathbb {F}$-basis of
$\mathbb {F}$-basis of ![]() $\sigma _{a-1,b+1}$, see [Reference PaškūnasPaš04, § 4.2.1]. By construction, we have
$\sigma _{a-1,b+1}$, see [Reference PaškūnasPaš04, § 4.2.1]. By construction, we have ![]() $e(v)=0$ and
$e(v)=0$ and ![]() $h(v)=(a-1)v$. Consider the following nonzero elements of
$h(v)=(a-1)v$. Consider the following nonzero elements of ![]() $\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}$:
$\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}$:
It is easy to see that ![]() $H$ acts on
$H$ acts on ![]() $l_1$ (respectively,
$l_1$ (respectively, ![]() $l_2$) by
$l_2$) by ![]() $\chi _{ a, b +1}$ (respectively,
$\chi _{ a, b +1}$ (respectively, ![]() $\chi _{ a - 2, b +2}$). Moreover, using the fact
$\chi _{ a - 2, b +2}$). Moreover, using the fact ![]() $ef(v)=fe(v)+h(v)=(a-1)v$, one checks that
$ef(v)=fe(v)+h(v)=(a-1)v$, one checks that ![]() $e(l_1)=e(l_2)=0$, so that
$e(l_1)=e(l_2)=0$, so that ![]() $l_1$ and
$l_1$ and ![]() $l_2$ are fixed by
$l_2$ are fixed by ![]() $U(\mathbb {Z}_p)$. Since
$U(\mathbb {Z}_p)$. Since ![]() $\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}\cong \sigma _{a,b+1}\oplus \sigma _{a-2,b+2}$, we deduce that
$\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}\cong \sigma _{a,b+1}\oplus \sigma _{a-2,b+2}$, we deduce that ![]() $l_1\in (\sigma _{a,b+1})^{U(\mathbb {Z}_p)}$ and
$l_1\in (\sigma _{a,b+1})^{U(\mathbb {Z}_p)}$ and ![]() $l_2\in (\sigma _{a-2,b+2})^{U(\mathbb {Z}_p)}$ under this decomposition. In particular,
$l_2\in (\sigma _{a-2,b+2})^{U(\mathbb {Z}_p)}$ under this decomposition. In particular, ![]() $\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}$ is generated by
$\mathrm {Sym}^1\mathbb {F}^2\otimes \sigma _{a-1,b+1}$ is generated by ![]() $l_1$ and
$l_1$ and ![]() $l_2$ as a
$l_2$ as a ![]() $K$-representation.
$K$-representation.
Since ![]() $\overline {\varphi }$ is
$\overline {\varphi }$ is ![]() $K$-equivariant, to finish the proof it suffices to prove that both
$K$-equivariant, to finish the proof it suffices to prove that both ![]() $l_1$ and
$l_1$ and ![]() $l_2$ lie in the image of
$l_2$ lie in the image of ![]() $\overline {\varphi }$. We let (recall
$\overline {\varphi }$. We let (recall ![]() $a\geq 3$)
$a\geq 3$)
be elements of ![]() $\frak {sl}_{2,\mathbb {F}_p} \otimes \sigma _{a-2,b+2}$ and claim that
$\frak {sl}_{2,\mathbb {F}_p} \otimes \sigma _{a-2,b+2}$ and claim that ![]() $\overline {\varphi }(w_i) = l_i$,
$\overline {\varphi }(w_i) = l_i$, ![]() $i=1,2$. Indeed, as
$i=1,2$. Indeed, as ![]() $\beta _{\underline {\mathrm {Sym}}^1 \mathcal {O}^2}(e\otimes X)=0$ and
$\beta _{\underline {\mathrm {Sym}}^1 \mathcal {O}^2}(e\otimes X)=0$ and ![]() $\beta _{\underline {\mathrm {Sym}}^1 \mathcal {O}^2}(e\otimes Y)=X$ by (3.12),
$\beta _{\underline {\mathrm {Sym}}^1 \mathcal {O}^2}(e\otimes Y)=X$ by (3.12),
 \begin{align*} \overline{\varphi} (w_1) &= \beta_L(e \otimes l_2) = \beta_L\bigg(e\otimes \bigg(Y\otimes v - \frac{1}{a-1} X \otimes f(v)\bigg)\bigg) \\ &= \beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2} (e\otimes Y) \otimes v - \frac{1}{a-1} \beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2} (e\otimes X) \otimes f(v) = X\otimes v = l_1. \end{align*}
\begin{align*} \overline{\varphi} (w_1) &= \beta_L(e \otimes l_2) = \beta_L\bigg(e\otimes \bigg(Y\otimes v - \frac{1}{a-1} X \otimes f(v)\bigg)\bigg) \\ &= \beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2} (e\otimes Y) \otimes v - \frac{1}{a-1} \beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2} (e\otimes X) \otimes f(v) = X\otimes v = l_1. \end{align*}
Similarly, ![]() $\overline {\varphi }(w_2) = \beta _L(-h\otimes l_2 - ({2}/({a-2})) e\otimes f(l_2))$. We have
$\overline {\varphi }(w_2) = \beta _L(-h\otimes l_2 - ({2}/({a-2})) e\otimes f(l_2))$. We have
 \begin{align*} f (l_2) &= f \bigg(Y\otimes v - \frac{1}{a-1} X \otimes f(v)\bigg)\\ &= Y \otimes f(v) - \frac{1}{a-1} (f(X) \otimes f(v) + X \otimes f^2(v))\\ &= \frac{a-2}{a-1}Y\otimes f(v) - \frac{1}{a-1}X \otimes f^2 (v), \end{align*}
\begin{align*} f (l_2) &= f \bigg(Y\otimes v - \frac{1}{a-1} X \otimes f(v)\bigg)\\ &= Y \otimes f(v) - \frac{1}{a-1} (f(X) \otimes f(v) + X \otimes f^2(v))\\ &= \frac{a-2}{a-1}Y\otimes f(v) - \frac{1}{a-1}X \otimes f^2 (v), \end{align*}
hence
 \begin{align*} \beta_L( e\otimes f (l_2)) &= \frac{a-2}{a-1}\beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2} (e\otimes Y) \otimes f(v) - \frac{1}{a-1} \beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2}(e\otimes X) \otimes f^2 (v) \\ &= \frac{a-2}{a-1} X\otimes f(v). \end{align*}
\begin{align*} \beta_L( e\otimes f (l_2)) &= \frac{a-2}{a-1}\beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2} (e\otimes Y) \otimes f(v) - \frac{1}{a-1} \beta_{\underline{\mathrm{Sym}}^1 \mathcal{O}^2}(e\otimes X) \otimes f^2 (v) \\ &= \frac{a-2}{a-1} X\otimes f(v). \end{align*}
As ![]() $h(X)=X$ and
$h(X)=X$ and ![]() $h(Y)=-Y$ by (3.12), we obtain
$h(Y)=-Y$ by (3.12), we obtain
 \begin{align*} \overline{\varphi} (w_2) &=- \beta_{L} \bigg(h \otimes \bigg(Y\otimes v - \frac{1}{a-1}X \otimes f(v)\bigg)\bigg) - \frac{2}{a-2}\cdot \frac{a-2}{a-1} X\otimes f(v) \\ &= Y \otimes v + \frac{1}{a-1}X \otimes f(v) - \frac{2}{a-1} X\otimes f(v) = l_2. \end{align*}
\begin{align*} \overline{\varphi} (w_2) &=- \beta_{L} \bigg(h \otimes \bigg(Y\otimes v - \frac{1}{a-1}X \otimes f(v)\bigg)\bigg) - \frac{2}{a-2}\cdot \frac{a-2}{a-1} X\otimes f(v) \\ &= Y \otimes v + \frac{1}{a-1}X \otimes f(v) - \frac{2}{a-1} X\otimes f(v) = l_2. \end{align*}
This proves the claim and finishes the proof of the proposition.
3.4 Gluing lattices
Assume ![]() $1 \leq a \leq p-3$. Consider the following three characters of
$1 \leq a \leq p-3$. Consider the following three characters of ![]() $\mathbb {F}_{p^2}^{\times }$:
$\mathbb {F}_{p^2}^{\times }$:
In this subsection, we construct a lattice ![]() $\widetilde {R}$ in
$\widetilde {R}$ in
such that ![]() $\widetilde {R} / p\widetilde {R}$ is killed by
$\widetilde {R} / p\widetilde {R}$ is killed by ![]() $\frak {m}_{K_1}^2$ and
$\frak {m}_{K_1}^2$ and ![]() $\mathrm {cosoc} (\widetilde {R} / p\widetilde {R}) = \sigma _{a,b+1}$. We divide the construction into two cases:
$\mathrm {cosoc} (\widetilde {R} / p\widetilde {R}) = \sigma _{a,b+1}$. We divide the construction into two cases: ![]() $1\leq a\leq p-4$ and
$1\leq a\leq p-4$ and ![]() $a=p-3$.
$a=p-3$.
3.4.1 The case  $1\,{\leq}\, a \,{\leq}\, p-4$
$1\,{\leq}\, a \,{\leq}\, p-4$
Denote by ![]() $W$ the nonsplit
$W$ the nonsplit ![]() $\Gamma$-extension
$\Gamma$-extension ![]() $( \sigma _{p- 3 - a, a + b + 2} \ \textbf {---}\ \sigma _{a, b+1})$.
$( \sigma _{p- 3 - a, a + b + 2} \ \textbf {---}\ \sigma _{a, b+1})$.
(1) Let
 $R_1$ be the unique (up to homothety) lattice in
$R_1$ be the unique (up to homothety) lattice in  $\Theta (\psi _1)$ such that
$\Theta (\psi _1)$ such that  $\mathrm {cosoc}(R_1/ p R_1) = \sigma _{a,b+1}$. Then
$\mathrm {cosoc}(R_1/ p R_1) = \sigma _{a,b+1}$. Then  $R_1/ p R_1\cong W$. Let
$R_1/ p R_1\cong W$. Let  $r_1$ denote the composite
$r_1$ denote the composite
 \[ r_1: R_1 \twoheadrightarrow R_1 / pR_1 \cong W. \]
\[ r_1: R_1 \twoheadrightarrow R_1 / pR_1 \cong W. \]
(2) By Proposition 3.6 and [Reference Breuil and PaškūnasBP12, Lem. 3.8], we have
with the convention \[ \operatorname{{\mathrm{JH}}}(\overline{\underline{\mathrm{Sym}}^1E^2\otimes\Theta(\psi_2)}^{\rm ss})= \{\sigma_{a,b+1},\sigma_{p-3-a,a+b+2},\sigma_{a+2,b},\sigma_{p-5-a,a+b+3}\} \]
\[ \operatorname{{\mathrm{JH}}}(\overline{\underline{\mathrm{Sym}}^1E^2\otimes\Theta(\psi_2)}^{\rm ss})= \{\sigma_{a,b+1},\sigma_{p-3-a,a+b+2},\sigma_{a+2,b},\sigma_{p-5-a,a+b+3}\} \]
 $\sigma _{-1,b}=0$. Let
$\sigma _{-1,b}=0$. Let  $R_2\subset \underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _2)$ be the unique (up to homothety) lattice such that
$R_2\subset \underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _2)$ be the unique (up to homothety) lattice such that  $\mathrm {cosoc}(R_2/ p R_2) = \sigma _{a,b+1}$. The structure of
$\mathrm {cosoc}(R_2/ p R_2) = \sigma _{a,b+1}$. The structure of  $R_2 / p R_2$ is given by Proposition 3.16, i.e.
(3.16)
$R_2 / p R_2$ is given by Proposition 3.16, i.e.
(3.16) \begin{equation} R_2/pR_2\cong(\sigma_{p-5-a,a+b+3}\ \textbf{---}\ \sigma_{a+2,b}\ \textbf{---}\ \sigma_{p-3-a,a+b+2}\ \textbf{---}\ \sigma_{a,b+1}). \end{equation}
\begin{equation} R_2/pR_2\cong(\sigma_{p-5-a,a+b+3}\ \textbf{---}\ \sigma_{a+2,b}\ \textbf{---}\ \sigma_{p-3-a,a+b+2}\ \textbf{---}\ \sigma_{a,b+1}). \end{equation}(3) By Proposition 3.6 and [Reference Breuil and PaškūnasBP12, Lemma 3.8], we have
with the convention \[ \operatorname{{\mathrm{JH}}}(\overline{\underline{\mathrm{Sym}}^1E^2\otimes\Theta(\psi_3)}^{\rm ss})= \{\sigma_{a,b+1},\sigma_{p-3-a,a+b+1},\sigma_{a-2,b+2},\sigma_{p-1-a,a+b+1}\} \]
\[ \operatorname{{\mathrm{JH}}}(\overline{\underline{\mathrm{Sym}}^1E^2\otimes\Theta(\psi_3)}^{\rm ss})= \{\sigma_{a,b+1},\sigma_{p-3-a,a+b+1},\sigma_{a-2,b+2},\sigma_{p-1-a,a+b+1}\} \]
 $\sigma _{-1,b+2}=0$. Let
$\sigma _{-1,b+2}=0$. Let  $R_3\subset \underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _3)$ be the unique (up to homothety) lattice such that
$R_3\subset \underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _3)$ be the unique (up to homothety) lattice such that  $\mathrm {cosoc}(R_3)\cong \sigma _{a,b+1}$. By Proposition 3.14,
$\mathrm {cosoc}(R_3)\cong \sigma _{a,b+1}$. By Proposition 3.14,  $R_3/pR_3$ has a cosocle filtration
(3.17)
$R_3/pR_3$ has a cosocle filtration
(3.17) \begin{equation} \sigma_{a-2, b+2} \ \textbf{---}\ ( \sigma_{p-1-a, a+b+1} \oplus \sigma_{p-3-a, a+b+2} ) \ \textbf{---}\ \sigma_{a, b+1}. \end{equation}
\begin{equation} \sigma_{a-2, b+2} \ \textbf{---}\ ( \sigma_{p-1-a, a+b+1} \oplus \sigma_{p-3-a, a+b+2} ) \ \textbf{---}\ \sigma_{a, b+1}. \end{equation}
Note that there exists a surjection ![]() $R_2\twoheadrightarrow W$ which we denote by
$R_2\twoheadrightarrow W$ which we denote by ![]() $r_2$; let
$r_2$; let ![]() $R_2':=\operatorname {{\mathrm {Ker}}}(r_2)$. The structure of
$R_2':=\operatorname {{\mathrm {Ker}}}(r_2)$. The structure of ![]() $R_2'/pR_2'$ is determined in Proposition 3.11(i). Precisely, it has a two-step socle and cosocle filtration
$R_2'/pR_2'$ is determined in Proposition 3.11(i). Precisely, it has a two-step socle and cosocle filtration
and all possible extensions do occur.
Similarly, there exists a surjection ![]() $R_3\twoheadrightarrow W$ which we denote by
$R_3\twoheadrightarrow W$ which we denote by ![]() $r_3$; let
$r_3$; let ![]() $R_3':=\operatorname {{\mathrm {Ker}}}(r_3)$. The structure of
$R_3':=\operatorname {{\mathrm {Ker}}}(r_3)$. The structure of ![]() $R_3'/pR_3'$ is also determined in Proposition 3.11(i). Precisely, it has a cosocle filtration
$R_3'/pR_3'$ is also determined in Proposition 3.11(i). Precisely, it has a cosocle filtration
and all possible extensions do occur.
3.4.2 Glue  $R_1$ and
$R_1$ and  $R_2$
$R_2$  $(1\leq a\leq p-4)$
$(1\leq a\leq p-4)$
Let ![]() $R$ be the lattice in
$R$ be the lattice in ![]() $\Theta (\psi _1) \oplus (\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi _2))$ obtained by gluing
$\Theta (\psi _1) \oplus (\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi _2))$ obtained by gluing ![]() $R_1$ and
$R_1$ and ![]() $R_2$ along
$R_2$ along ![]() $W$, i.e.
$W$, i.e. ![]() $R$ is given by the short exact sequence
$R$ is given by the short exact sequence
Let ![]() $r_{R}$ denote the composition
$r_{R}$ denote the composition ![]() $R \twoheadrightarrow R/pR \twoheadrightarrow R_1/pR_1 \cong W$.
$R \twoheadrightarrow R/pR \twoheadrightarrow R_1/pR_1 \cong W$.
Lemma 3.18 We have that:
(i)
 $r_R$ induces a short exact sequence
(3.21)in particular,
$r_R$ induces a short exact sequence
(3.21)in particular, \begin{equation} 0 \to R_2' / p R_2' \rightarrow R /p R \to W \to 0 ; \end{equation}
\begin{equation} 0 \to R_2' / p R_2' \rightarrow R /p R \to W \to 0 ; \end{equation} $R/ pR$ is killed by
$R/ pR$ is killed by  $\frak {m}_{K_1}^2$;
$\frak {m}_{K_1}^2$;(ii)
 $\operatorname {{\mathrm {Ker}}}(r_R)=R_2'+pR$ and
$\operatorname {{\mathrm {Ker}}}(r_R)=R_2'+pR$ and
 \[ \operatorname{{\mathrm{Ker}}}(r_R)/p\operatorname{{\mathrm{Ker}}}(r_R)\cong R_2'/pR_2'\oplus W. \]
\[ \operatorname{{\mathrm{Ker}}}(r_R)/p\operatorname{{\mathrm{Ker}}}(r_R)\cong R_2'/pR_2'\oplus W. \]
Proof. This is a special case of Lemma 3.3 applied to ![]() $L_1=R_2$ and
$L_1=R_2$ and ![]() $L_2=R_1$.
$L_2=R_1$.
Proposition 3.19 The short exact sequence (3.21) induces an isomorphism ![]() $(R/pR)_{K_1} \cong W$. In particular,
$(R/pR)_{K_1} \cong W$. In particular, ![]() $\mathrm {cosoc} (R/ p R) = \sigma _{a,b+1}$.
$\mathrm {cosoc} (R/ p R) = \sigma _{a,b+1}$.
Proof. By Lemma 3.18(i), it suffices to show that for any ![]() $x \in R_2'$, there exist
$x \in R_2'$, there exist ![]() $r\in \mathbb {N}$,
$r\in \mathbb {N}$, ![]() $k_1,\ldots, k_r \in K_1$,
$k_1,\ldots, k_r \in K_1$, ![]() $v_1,\ldots, v_r \in R$ such that
$v_1,\ldots, v_r \in R$ such that ![]() $x= (k_1 -1) v_1 + \cdots + (k_r - 1) v_r$. By Proposition 3.17 (applied to
$x= (k_1 -1) v_1 + \cdots + (k_r - 1) v_r$. By Proposition 3.17 (applied to ![]() $L=p^{-1}R_2'$ and
$L=p^{-1}R_2'$ and ![]() $L_2=R_2$), there exist
$L_2=R_2$), there exist ![]() $r\in \mathbb {N}$,
$r\in \mathbb {N}$, ![]() $k_1,\ldots, k_r \in K_1$,
$k_1,\ldots, k_r \in K_1$, ![]() $y_1,\ldots, y_r \in R_2$ such that
$y_1,\ldots, y_r \in R_2$ such that
For ![]() $1\leq i \leq r$, choose
$1\leq i \leq r$, choose ![]() $z_i \in R_1$ such that
$z_i \in R_1$ such that ![]() $r_1(z_i) = r_2 (y_i)$ and let
$r_1(z_i) = r_2 (y_i)$ and let ![]() $v_i = (z_i,y_i)\in R$. Since
$v_i = (z_i,y_i)\in R$. Since ![]() $K_1$ acts trivially on
$K_1$ acts trivially on ![]() $R_1$, we have
$R_1$, we have
 \[ (0, x) = \bigg(\sum_{i=1}^r (k_i -1) z_i, \sum_{i=1}^r (k_i -1) y_i\bigg) = \sum_{i=1}^r (k_i - 1) v_i, \]
\[ (0, x) = \bigg(\sum_{i=1}^r (k_i -1) z_i, \sum_{i=1}^r (k_i -1) y_i\bigg) = \sum_{i=1}^r (k_i - 1) v_i, \]
giving the result.
3.4.3 Glue  $R$ and
$R$ and  $R'_3$
$R'_3$  $(1\leq a\leq p-4)$
$(1\leq a\leq p-4)$
We define ![]() $\widetilde {R}$ to be the lattice in
$\widetilde {R}$ to be the lattice in ![]() $\Theta (\psi _1)\oplus (\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _2))\oplus (\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _3))$ obtained by gluing
$\Theta (\psi _1)\oplus (\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _2))\oplus (\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _3))$ obtained by gluing ![]() $R$ and
$R$ and ![]() $R_3$ along
$R_3$ along ![]() $W$, i.e.
$W$, i.e.
(i) There exists a short exact sequence
 \[ 0 \to \operatorname{{\mathrm{Ker}}}(r_R) / p \operatorname{{\mathrm{Ker}}}(r_R) \rightarrow \widetilde{R} /p \widetilde{R} \to R_3/pR_3 \to 0. \]
\[ 0 \to \operatorname{{\mathrm{Ker}}}(r_R) / p \operatorname{{\mathrm{Ker}}}(r_R) \rightarrow \widetilde{R} /p \widetilde{R} \to R_3/pR_3 \to 0. \]
(ii) We have
 $\mathrm {cosoc} (\widetilde {R}/ p \widetilde {R}) = \sigma _{a,b+1}$.
$\mathrm {cosoc} (\widetilde {R}/ p \widetilde {R}) = \sigma _{a,b+1}$.
Proof. (i) This is a special case of Lemma 3.3.
(ii) This is a special case of Lemma 3.4, with ![]() $L_1=R$ and
$L_1=R$ and ![]() $L_2=R_3$. First, condition (a) in Lemma 3.4 holds by Proposition 3.19. Second, we have
$L_2=R_3$. First, condition (a) in Lemma 3.4 holds by Proposition 3.19. Second, we have
by (3.18) and Lemma 3.18(ii), and
Proposition 3.21 Let ![]() $V$ denote the quotient of
$V$ denote the quotient of ![]() $R_3/pR_3$ by
$R_3/pR_3$ by ![]() $\sigma _{a-2,b+2}$ via (3.17). Then there exists a short exact sequence
$\sigma _{a-2,b+2}$ via (3.17). Then there exists a short exact sequence
In particular, ![]() $\widetilde {R} / p\widetilde {R}$ is killed by
$\widetilde {R} / p\widetilde {R}$ is killed by ![]() $\frak {m}_{K_1}^2$.
$\frak {m}_{K_1}^2$.
Proof. By definition, we have
Note that ![]() $\sigma _{a-2, b+2}$ has no nontrivial extensions with any Jordan–Hölder factor of
$\sigma _{a-2, b+2}$ has no nontrivial extensions with any Jordan–Hölder factor of ![]() $W$ and of
$W$ and of ![]() $R_2 / pR_2$, using [Reference Breuil and PaškūnasBP12, Corollary 5.6] and Lemma 3.22 below. The result easily follows by Proposition 3.20.
$R_2 / pR_2$, using [Reference Breuil and PaškūnasBP12, Corollary 5.6] and Lemma 3.22 below. The result easily follows by Proposition 3.20.
Lemma 3.22 Assume ![]() $2\leq a\leq p-2$. Then
$2\leq a\leq p-2$. Then ![]() $\operatorname {{\mathrm {Ext}}}^1_{K}(\sigma _{a-2,b+2}, \sigma _{a,b+1})=0$.
$\operatorname {{\mathrm {Ext}}}^1_{K}(\sigma _{a-2,b+2}, \sigma _{a,b+1})=0$.
Proof. We have a short exact sequence ![]() $0\rightarrow \sigma _{p+1-a,a+b}\rightarrow \operatorname {{\mathrm {Ind}}}_I^{K}\chi _{a-2,b+2}\rightarrow \sigma _{a-2,b+2}\rightarrow 0$. Since
$0\rightarrow \sigma _{p+1-a,a+b}\rightarrow \operatorname {{\mathrm {Ind}}}_I^{K}\chi _{a-2,b+2}\rightarrow \sigma _{a-2,b+2}\rightarrow 0$. Since ![]() $\operatorname {{\mathrm {Ext}}}^1_{K}(\sigma _{p+1-a,a+b},\sigma _{a,b+1})=0$ by [Reference Breuil and PaškūnasBP12, Corollary 5.6], we are reduced to proving
$\operatorname {{\mathrm {Ext}}}^1_{K}(\sigma _{p+1-a,a+b},\sigma _{a,b+1})=0$ by [Reference Breuil and PaškūnasBP12, Corollary 5.6], we are reduced to proving
equivalently ![]() $\operatorname {{\mathrm {Ext}}}^1_{I}(\chi _{a-2,b+2},\sigma _{a,b+1})=0$ by Frobenius reciprocity.
$\operatorname {{\mathrm {Ext}}}^1_{I}(\chi _{a-2,b+2},\sigma _{a,b+1})=0$ by Frobenius reciprocity.
Consider an ![]() $I$-extension
$I$-extension ![]() $0\rightarrow \sigma _{a,b+1}|_I\rightarrow \mathcal {E}\rightarrow \chi _{a-2,b+2}\rightarrow 0$. We first prove that it splits as
$0\rightarrow \sigma _{a,b+1}|_I\rightarrow \mathcal {E}\rightarrow \chi _{a-2,b+2}\rightarrow 0$. We first prove that it splits as ![]() $U(\mathbb {Z}_p)$-representation. Since
$U(\mathbb {Z}_p)$-representation. Since ![]() $\sigma _{a,b+1}$ is a cyclic
$\sigma _{a,b+1}$ is a cyclic ![]() $\mathbb {F}[\![U(\mathbb {Z}_p)]\!]$-module, we have
$\mathbb {F}[\![U(\mathbb {Z}_p)]\!]$-module, we have ![]() $H^1(U(\mathbb {Z}_p),\sigma _{a,b+1})\cong H^1(U(\mathbb {Z}_p),\chi _{a,b+1}^s)$, where
$H^1(U(\mathbb {Z}_p),\sigma _{a,b+1})\cong H^1(U(\mathbb {Z}_p),\chi _{a,b+1}^s)$, where ![]() $\chi _{a,b+1}^s$ is identified with the
$\chi _{a,b+1}^s$ is identified with the ![]() $U(\mathbb {Z}_p)$-cosocle of
$U(\mathbb {Z}_p)$-cosocle of ![]() $\sigma _{a,b+1}$. As seen in the proof of Proposition 3.1, we get
$\sigma _{a,b+1}$. As seen in the proof of Proposition 3.1, we get
As ![]() $2\leq a\leq p-2$, this implies
$2\leq a\leq p-2$, this implies ![]() $\chi _{a-2,b+2}\neq \chi _{a,b+1}^s\alpha ^{-1}$, and so
$\chi _{a-2,b+2}\neq \chi _{a,b+1}^s\alpha ^{-1}$, and so ![]() $\operatorname {{\mathrm {Ext}}}^1_{U(\mathbb {Z}_p)}(\chi _{a-2,b+2},\sigma _{a,b+1})=0$.
$\operatorname {{\mathrm {Ext}}}^1_{U(\mathbb {Z}_p)}(\chi _{a-2,b+2},\sigma _{a,b+1})=0$.
As a consequence, we may choose ![]() $v\in \mathcal {E}$ which is fixed by
$v\in \mathcal {E}$ which is fixed by ![]() $U(\mathbb {Z}_p)$ and on which
$U(\mathbb {Z}_p)$ and on which ![]() $H$ acts via
$H$ acts via ![]() $\chi _{a-2,b+2}$. Next, as in the proof of [Reference PaškūnasPaš10, Proposition 7.2], we show that
$\chi _{a-2,b+2}$. Next, as in the proof of [Reference PaškūnasPaš10, Proposition 7.2], we show that ![]() $v$ is actually fixed by
$v$ is actually fixed by ![]() $I_1$, showing that
$I_1$, showing that ![]() $\mathcal {E}$ splits as
$\mathcal {E}$ splits as ![]() $I$-representation. This finishes the proof.
$I$-representation. This finishes the proof.
We obtain the following corollary.
Corollary 3.23 We have that ![]() $\widetilde {R} / p \widetilde {R}$ has cosocle
$\widetilde {R} / p \widetilde {R}$ has cosocle ![]() $\sigma _{a,b+1}$ and is a quotient of
$\sigma _{a,b+1}$ and is a quotient of ![]() $(\operatorname {{\mathrm {Proj}}}_{\mathcal {O}[\![K/Z_1]\!]}\sigma _{a,b+1}) / \frak {m}_{K_1}^2$.
$(\operatorname {{\mathrm {Proj}}}_{\mathcal {O}[\![K/Z_1]\!]}\sigma _{a,b+1}) / \frak {m}_{K_1}^2$.
3.4.4 The case  $a = p-3$
$a = p-3$
In this case, we need to slightly modify the above construction. We only sketch the construction and leave the detail to the reader.
(1) Let
 $R_1$ be the unique (up to homothety) lattice in
$R_1$ be the unique (up to homothety) lattice in  $\Theta (\psi _1)$ such that
$\Theta (\psi _1)$ such that  $\mathrm {cosoc}(R_1/ p R_1) = \sigma _{p-3,b+1}$. Then
Let
$\mathrm {cosoc}(R_1/ p R_1) = \sigma _{p-3,b+1}$. Then
Let \[ R_1/ p R_1\cong (\sigma_{0,b} \ \textbf{---}\ \sigma_{p-3,b+1}) = : W. \]
\[ R_1/ p R_1\cong (\sigma_{0,b} \ \textbf{---}\ \sigma_{p-3,b+1}) = : W. \]
 $r_1$ denote the projection
$r_1$ denote the projection  $R_1 \twoheadrightarrow \sigma _{p-3,b+1}$.
$R_1 \twoheadrightarrow \sigma _{p-3,b+1}$.(2) By Proposition 3.6 and [Reference Breuil and PaškūnasBP12, Lemma 3.8], we have
Let \[ \operatorname{{\mathrm{JH}}}(\overline{\underline{\mathrm{Sym}}^1 \mathcal{O}^2 \otimes \Theta(\psi_2)}^{\rm ss})=\{\sigma_{p-1,b},\sigma_{p-3,b+1}\}. \]
\[ \operatorname{{\mathrm{JH}}}(\overline{\underline{\mathrm{Sym}}^1 \mathcal{O}^2 \otimes \Theta(\psi_2)}^{\rm ss})=\{\sigma_{p-1,b},\sigma_{p-3,b+1}\}. \]
 $R_2$ be the unique lattice in
$R_2$ be the unique lattice in  $\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi _2)$ such that
$\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi _2)$ such that  $\mathrm {cosoc} (R_2/pR_2) = \sigma _{p-3, b+1}$. Then
Let
$\mathrm {cosoc} (R_2/pR_2) = \sigma _{p-3, b+1}$. Then
Let \[ R_2/pR_2\cong(\sigma_{p-1,b}\ \textbf{---}\ \sigma_{p-3,b+1}). \]
\[ R_2/pR_2\cong(\sigma_{p-1,b}\ \textbf{---}\ \sigma_{p-3,b+1}). \]
 $r_2$ denote the projection
$r_2$ denote the projection  $R_2\twoheadrightarrow \sigma _{p-3,b+1}$ and
$R_2\twoheadrightarrow \sigma _{p-3,b+1}$ and  $R_2':=\operatorname {{\mathrm {Ker}}}(r_2)$. Proposition 3.13 implies that
$R_2':=\operatorname {{\mathrm {Ker}}}(r_2)$. Proposition 3.13 implies that
 \[ R_2'/pR_2'\cong \sigma_{p-3,b+1}\oplus\sigma_{p-1,b}. \]
\[ R_2'/pR_2'\cong \sigma_{p-3,b+1}\oplus\sigma_{p-1,b}. \]
(3) Let
 $R_3$ and
$R_3$ and  $R'_3$ be the lattices in
$R'_3$ be the lattices in  $\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi _3)$ constructed as in the case
$\underline {\mathrm {Sym}}^1 E^2 \otimes \Theta (\psi _3)$ constructed as in the case  $1\leq a\leq p-4$. Namely,
$1\leq a\leq p-4$. Namely,  $R_3$ has cosocle
$R_3$ has cosocle  $\sigma _{p-3,b+1}$, and
$\sigma _{p-3,b+1}$, and  $R_3':=\operatorname {{\mathrm {Ker}}}(r_3)$ where
$R_3':=\operatorname {{\mathrm {Ker}}}(r_3)$ where  $r_3$ denotes the projection
$r_3$ denotes the projection  $R_3\twoheadrightarrow W$.
$R_3\twoheadrightarrow W$.
We first glue ![]() $R_1$ and
$R_1$ and ![]() $R_2$ along
$R_2$ along ![]() $\sigma _{p-3,b+1}$, namely
$\sigma _{p-3,b+1}$, namely
Then by Lemma 3.3(i) there is a short exact sequence
Moreover, as in the proof of Proposition 3.19 one can show that ![]() $r_R$ induces an isomorphism
$r_R$ induces an isomorphism ![]() $(R/pR)_{K_1} \cong W$. In particular,
$(R/pR)_{K_1} \cong W$. In particular, ![]() $\mathrm {cosoc}(R/pR)\cong \sigma _{p-3,b+1}$.
$\mathrm {cosoc}(R/pR)\cong \sigma _{p-3,b+1}$.
The gluing of ![]() $R$ and
$R$ and ![]() $R_3$ is exactly as in the case
$R_3$ is exactly as in the case ![]() $1\leq a \leq p-4$. Let
$1\leq a \leq p-4$. Let ![]() $\widetilde {R}$ be defined by
$\widetilde {R}$ be defined by
One can follow the proof of Proposition 3.21 and Corollary 3.23, to show the following result.
(i) We have that
 $\widetilde {R} / p \widetilde {R}$ has cosocle
$\widetilde {R} / p \widetilde {R}$ has cosocle  $\sigma _{p-3,b+1}$.
$\sigma _{p-3,b+1}$.(ii) Let
 $V$ denote the quotient of
$V$ denote the quotient of  $R_3/pR_3$ by
$R_3/pR_3$ by  $\sigma _{p-5,b+2}$. Then there is a short exact sequence
(3.24)As a consequence,
$\sigma _{p-5,b+2}$. Then there is a short exact sequence
(3.24)As a consequence, \begin{equation} 0 \to W \oplus R'_2/ p R'_2 \oplus \sigma_{p-5, b+2} \to \widetilde{R} / p\widetilde{R} \to V \to 0. \end{equation}
\begin{equation} 0 \to W \oplus R'_2/ p R'_2 \oplus \sigma_{p-5, b+2} \to \widetilde{R} / p\widetilde{R} \to V \to 0. \end{equation} $\widetilde {R} / p \widetilde {R}$ is a quotient of
$\widetilde {R} / p \widetilde {R}$ is a quotient of  $(\operatorname {{\mathrm {Proj}}}_{ \mathcal {O}[\![K/Z_1]\!]}\sigma _{p-3,b+1}) / \frak {m}_{K_1}^2$.
$(\operatorname {{\mathrm {Proj}}}_{ \mathcal {O}[\![K/Z_1]\!]}\sigma _{p-3,b+1}) / \frak {m}_{K_1}^2$.
4. Galois deformation rings
Assume ![]() $p\geq 5$. Let
$p\geq 5$. Let ![]() $\overline {\rho }: G_{\mathbb {Q}_p}\to \mathrm {GL}_2(\mathbb {F})$ be a two-dimensional continuous representation of
$\overline {\rho }: G_{\mathbb {Q}_p}\to \mathrm {GL}_2(\mathbb {F})$ be a two-dimensional continuous representation of ![]() $G_{\mathbb {Q}_p} = \operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p / \mathbb {Q}_p)$. In this section, we study the congruence relation of Galois deformation rings of different (tame) types. Our method does not allow us to determine the precise structure of the Galois deformation rings, but is enough for application in § 6.3.
$G_{\mathbb {Q}_p} = \operatorname {{\mathrm {Gal}}}(\overline {\mathbb {Q}}_p / \mathbb {Q}_p)$. In this section, we study the congruence relation of Galois deformation rings of different (tame) types. Our method does not allow us to determine the precise structure of the Galois deformation rings, but is enough for application in § 6.3.
4.1 Preliminaries
We collect some results on the set of Serre weights associated to ![]() $\overline {\rho }$ and some results of Paškūnas and of Morra. We prove in § 4.2.2 a criterion for some Galois deformation rings to be regular.
$\overline {\rho }$ and some results of Paškūnas and of Morra. We prove in § 4.2.2 a criterion for some Galois deformation rings to be regular.
4.1.1 Serre weights
Let ![]() $\omega$ (respectively,
$\omega$ (respectively, ![]() $\omega _2$) be the mod
$\omega _2$) be the mod ![]() $p$ cyclotomic character (respectively, Serre's fundamental character of niveau 2) of
$p$ cyclotomic character (respectively, Serre's fundamental character of niveau 2) of ![]() $G_{\mathbb {Q}_p}$. Up to isomorphism,
$G_{\mathbb {Q}_p}$. Up to isomorphism, ![]() $\overline {\rho }$ has one of the following forms:
$\overline {\rho }$ has one of the following forms:
Case 1.
 $\overline {\rho }$ is absolutely irreducible and
$\overline {\rho }$ is absolutely irreducible and  $\overline {\rho }|_{I_p} \sim \big (\begin{smallmatrix} \omega _{2}^{r+1} & 0 \\ 0 & \omega _2^{p(r+1)} \end{smallmatrix} \big ) \otimes \omega ^{s+1}$,
$\overline {\rho }|_{I_p} \sim \big (\begin{smallmatrix} \omega _{2}^{r+1} & 0 \\ 0 & \omega _2^{p(r+1)} \end{smallmatrix} \big ) \otimes \omega ^{s+1}$,  $0\leq r\leq p-1$,
$0\leq r\leq p-1$,  $0\leq s \leq p-2$;
$0\leq s \leq p-2$;Case 2.
 $\overline {\rho } \sim \big (\begin{smallmatrix} {\rm unr}_1 \omega ^{r+1} & * \\ 0 & {\rm unr}_2 \end{smallmatrix} \big ) \otimes \omega ^{s+1}$ is reducible nonsplit, where
$\overline {\rho } \sim \big (\begin{smallmatrix} {\rm unr}_1 \omega ^{r+1} & * \\ 0 & {\rm unr}_2 \end{smallmatrix} \big ) \otimes \omega ^{s+1}$ is reducible nonsplit, where  ${\rm unr}_1$,
${\rm unr}_1$,  ${\rm unr}_2$ are unramified characters, and
${\rm unr}_2$ are unramified characters, and  $0\leq r \leq p-2$,
$0\leq r \leq p-2$,  $0\leq s \leq p-2$;
$0\leq s \leq p-2$;Case 3.
 $\overline {\rho } \sim \big (\begin{smallmatrix} {\rm unr}_1 \omega ^{r+1} & 0 \\ 0 & {\rm unr}_2 \end{smallmatrix} \big ) \otimes \omega ^{s+1}$ is reducible split, where
$\overline {\rho } \sim \big (\begin{smallmatrix} {\rm unr}_1 \omega ^{r+1} & 0 \\ 0 & {\rm unr}_2 \end{smallmatrix} \big ) \otimes \omega ^{s+1}$ is reducible split, where  ${\rm unr}_1$,
${\rm unr}_1$,  ${\rm unr}_2$ are unramified characters, and
${\rm unr}_2$ are unramified characters, and  $0 \leq r\leq p-2$,
$0 \leq r\leq p-2$,  $0\leq s \leq p-2$.
$0\leq s \leq p-2$.
Let ![]() $W(\overline {\rho })$ be the set of Serre weights associated to
$W(\overline {\rho })$ be the set of Serre weights associated to ![]() $\overline {\rho }$ in [Reference Buzzard, Diamond and JarvisBDJ10]. We have the following explicit description of
$\overline {\rho }$ in [Reference Buzzard, Diamond and JarvisBDJ10]. We have the following explicit description of ![]() $W(\overline {\rho })$.
$W(\overline {\rho })$.
Theorem 4.1 [Reference Buzzard, Diamond and JarvisBDJ10, Theorem 3.17]
(i) Assume
 $\overline {\rho }$ is in case 1. Then
$\overline {\rho }$ is in case 1. Then  $W(\overline {\rho })= \{\sigma _{r,s+1},\ \sigma _{p-1-r, r+s+1}\}$.
$W(\overline {\rho })= \{\sigma _{r,s+1},\ \sigma _{p-1-r, r+s+1}\}$.(ii) Assume
 $\overline {\rho }$ is in case 2.
$\overline {\rho }$ is in case 2.(a) If
 $r \neq 0$, then
$r \neq 0$, then  $W(\overline {\rho })= \{\sigma _{r, s+1}\}$.
$W(\overline {\rho })= \{\sigma _{r, s+1}\}$.(b) If
 $r=0$,
$r=0$,  ${\rm unr}_1 = {\rm unr}_2$ and
${\rm unr}_1 = {\rm unr}_2$ and  $\overline {\rho }$ is très ramifié, then
$\overline {\rho }$ is très ramifié, then  $W(\overline {\rho }) =\{ \sigma _{p-1,s+1}\}$.
$W(\overline {\rho }) =\{ \sigma _{p-1,s+1}\}$.(c) For other
 $\overline {\rho }$,
$\overline {\rho }$,  $W(\overline {\rho })= \{ \sigma _{0,s+1},\ \sigma _{p-1,s+1}\}$.
$W(\overline {\rho })= \{ \sigma _{0,s+1},\ \sigma _{p-1,s+1}\}$.
(iii) Assume
 $\overline {\rho }$ is in case 3.
$\overline {\rho }$ is in case 3.
(a) If
 $1\leq r\leq p-4$, then
$1\leq r\leq p-4$, then  $W(\overline {\rho })=\{ \sigma _{r,s+1},\ \sigma _{p-3-r, r+s+2}\}$.
$W(\overline {\rho })=\{ \sigma _{r,s+1},\ \sigma _{p-3-r, r+s+2}\}$.(b) If
 $r = 0$, then
$r = 0$, then  $W(\overline {\rho }) =\{ \sigma _{0,s+1},\ \sigma _{p-3, s+2},\ \sigma _{p-1, s+1} \}$.
$W(\overline {\rho }) =\{ \sigma _{0,s+1},\ \sigma _{p-3, s+2},\ \sigma _{p-1, s+1} \}$.(c) If
 $r = p-3$, then
$r = p-3$, then  $W(\overline {\rho })=\{ \sigma _{0, s},\ \sigma _{p-3,s+1},\ \sigma _{p-1, s} \}$.
$W(\overline {\rho })=\{ \sigma _{0, s},\ \sigma _{p-3,s+1},\ \sigma _{p-1, s} \}$.(d) If
 $r = p-2$, then
$r = p-2$, then  $W(\overline {\rho })=\{ \sigma _{p-2, s+1}\}$.
$W(\overline {\rho })=\{ \sigma _{p-2, s+1}\}$.
4.2 Mod  $p$ representations of
$p$ representations of  $\mathrm {GL}_2(\mathbb {Q}_p)$
$\mathrm {GL}_2(\mathbb {Q}_p)$
Assume that ![]() $\overline {\rho }$ satisfies
$\overline {\rho }$ satisfies ![]() $\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })\cong \mathbb {F}$. We associate to
$\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })\cong \mathbb {F}$. We associate to ![]() $\overline {\rho }$ an admissible smooth
$\overline {\rho }$ an admissible smooth ![]() $\mathbb {F}$-representation
$\mathbb {F}$-representation ![]() $\pi (\overline {\rho })$ of
$\pi (\overline {\rho })$ of ![]() $G:=\mathrm {GL}_2(\mathbb {Q}_p)$ as follows.
$G:=\mathrm {GL}_2(\mathbb {Q}_p)$ as follows.
Case 1. If
 $\overline {\rho }$ is absolutely irreducible, then
$\overline {\rho }$ is absolutely irreducible, then  $\pi (\overline {\rho })$ is the irreducible supersingular representation of
$\pi (\overline {\rho })$ is the irreducible supersingular representation of  $G$ associated to
$G$ associated to  $\overline {\rho }$ by the mod
$\overline {\rho }$ by the mod  $p$ local Langlands correspondence defined in [Reference BreuilBre03].
$p$ local Langlands correspondence defined in [Reference BreuilBre03].Case 2. If
 $\overline {\rho } \sim \big (\begin{smallmatrix} \chi _1 & * \\ 0 & \chi _2 \end{smallmatrix}\big )$ with
$\overline {\rho } \sim \big (\begin{smallmatrix} \chi _1 & * \\ 0 & \chi _2 \end{smallmatrix}\big )$ with  $\chi _1 \chi _2^{-1} \neq \omega ^{\pm 1}, \mathbf {1}$, then there is an exact nonsplit sequence
If
$\chi _1 \chi _2^{-1} \neq \omega ^{\pm 1}, \mathbf {1}$, then there is an exact nonsplit sequence
If \[ 0 \to \operatorname{{\mathrm{Ind}}}_{B(\mathbb{Q}_p)}^{G} \chi_2\otimes \chi_1 \omega^{-1} \to \pi(\overline{\rho}) \to \operatorname{{\mathrm{Ind}}}_{B(\mathbb{Q}_p)}^{G} \chi_1\otimes \chi_2 \omega^{-1} \to 0. \]
\[ 0 \to \operatorname{{\mathrm{Ind}}}_{B(\mathbb{Q}_p)}^{G} \chi_2\otimes \chi_1 \omega^{-1} \to \pi(\overline{\rho}) \to \operatorname{{\mathrm{Ind}}}_{B(\mathbb{Q}_p)}^{G} \chi_1\otimes \chi_2 \omega^{-1} \to 0. \]
 $\overline {\rho } \sim \big (\begin{smallmatrix} \chi & * \\ 0 & \chi \omega \end{smallmatrix}\big )$, then there is an exact nonsplit sequence
where
$\overline {\rho } \sim \big (\begin{smallmatrix} \chi & * \\ 0 & \chi \omega \end{smallmatrix}\big )$, then there is an exact nonsplit sequence
where \[ 0\to \operatorname{{\mathrm{Ind}}}_{B(\mathbb{Q}_p)}^{G} \chi\omega \otimes \chi\omega^{-1} \to \pi(\overline{\rho}) \to \tau_1 \otimes \chi\circ \det \to 0, \]
\[ 0\to \operatorname{{\mathrm{Ind}}}_{B(\mathbb{Q}_p)}^{G} \chi\omega \otimes \chi\omega^{-1} \to \pi(\overline{\rho}) \to \tau_1 \otimes \chi\circ \det \to 0, \]
 ${\rm Sp}$ is the Steinberg representation of
${\rm Sp}$ is the Steinberg representation of  $G$ and
$G$ and  $\tau _1$ is a nonsplit extension
$\tau _1$ is a nonsplit extension  $0 \to {\rm Sp} \to \tau _1 \to \mathbf {1}_G^{\oplus 2} \to 0$ with
$0 \to {\rm Sp} \to \tau _1 \to \mathbf {1}_G^{\oplus 2} \to 0$ with  $\operatorname {{\mathrm {soc}}}_G(\tau _1)=\operatorname {{\mathrm {Sp}}}$.
$\operatorname {{\mathrm {soc}}}_G(\tau _1)=\operatorname {{\mathrm {Sp}}}$.
If
 $\overline {\rho }\sim \big (\begin{smallmatrix} {\chi \omega } & {*}\\ {0} & {\chi }\end{smallmatrix}\big )$, then
$\overline {\rho }\sim \big (\begin{smallmatrix} {\chi \omega } & {*}\\ {0} & {\chi }\end{smallmatrix}\big )$, then  $\pi (\overline {\rho })$ is the representation defined in [Reference PaškūnasPaš15, Lemma 6.7] (denoted by
$\pi (\overline {\rho })$ is the representation defined in [Reference PaškūnasPaš15, Lemma 6.7] (denoted by  $\beta$ there). Its precise structure will be recalled in § 8.3.
$\beta$ there). Its precise structure will be recalled in § 8.3.
We remark that the representation ![]() $\pi (\overline {\rho })$ is just the representation corresponding to
$\pi (\overline {\rho })$ is just the representation corresponding to ![]() $\overline {\rho }$ in the mod
$\overline {\rho }$ in the mod ![]() $p$ local Langlands correspondence for
$p$ local Langlands correspondence for ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$, except in the case
$\mathrm {GL}_2(\mathbb {Q}_p)$, except in the case ![]() $\overline {\rho }\sim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$,
$\overline {\rho }\sim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$, ![]() $\pi (\overline {\rho })$ has one extra copy of
$\pi (\overline {\rho })$ has one extra copy of ![]() $\chi \circ \det$ than the usual form.
$\chi \circ \det$ than the usual form.
The following theorem is a consequence of results of Morra [Reference MorraMor11, Reference MorraMor17].
Theorem 4.2 Assume ![]() $\overline {\rho }$ is either in case 1 of § 4.1.1 with
$\overline {\rho }$ is either in case 1 of § 4.1.1 with ![]() $r\notin \{1,p-2\}$ or
$r\notin \{1,p-2\}$ or ![]() $\overline {\rho }$ is in case 2 of § 4.1.1 with
$\overline {\rho }$ is in case 2 of § 4.1.1 with ![]() $1 \leq r\leq p-3$.Footnote 3 Then for any
$1 \leq r\leq p-3$.Footnote 3 Then for any ![]() $\sigma \in W(\overline {\rho })$,
$\sigma \in W(\overline {\rho })$, ![]() $\sigma$ occurs in
$\sigma$ occurs in ![]() $\pi (\overline {\rho }) [\frak {m}_{K_1}^2]$ with multiplicity one.
$\pi (\overline {\rho }) [\frak {m}_{K_1}^2]$ with multiplicity one.
Proof. If ![]() $\overline {\rho }$ is absolutely irreducible, then
$\overline {\rho }$ is absolutely irreducible, then ![]() $\pi (\overline {\rho })$ is the representation
$\pi (\overline {\rho })$ is the representation ![]() $\pi (\overline {\rho })$ in [Reference MorraMor11] whose
$\pi (\overline {\rho })$ in [Reference MorraMor11] whose ![]() $K$-socle filtration is given by [Reference MorraMor11, Theorem 1.1]. If
$K$-socle filtration is given by [Reference MorraMor11, Theorem 1.1]. If ![]() $\overline {\rho }$ is reducible nonsplit and
$\overline {\rho }$ is reducible nonsplit and ![]() $\overline {\rho } \nsim \big (\begin{smallmatrix} \mathbf {1} & * \\ 0 & \omega \end{smallmatrix}\big ) \otimes \chi$, then
$\overline {\rho } \nsim \big (\begin{smallmatrix} \mathbf {1} & * \\ 0 & \omega \end{smallmatrix}\big ) \otimes \chi$, then ![]() $\pi (\overline {\rho })$ is equal to the representation
$\pi (\overline {\rho })$ is equal to the representation ![]() $A_{r,\lambda }$ (in [Reference MorraMor17, Theorem 1.1]) for some
$A_{r,\lambda }$ (in [Reference MorraMor17, Theorem 1.1]) for some ![]() $\lambda \in \mathbb {F}^{\times }$. If
$\lambda \in \mathbb {F}^{\times }$. If ![]() $\overline {\rho } \sim \big (\begin{smallmatrix} \mathbf {1} & * \\ 0 & \omega \end{smallmatrix}\big ) \otimes \chi$, then
$\overline {\rho } \sim \big (\begin{smallmatrix} \mathbf {1} & * \\ 0 & \omega \end{smallmatrix}\big ) \otimes \chi$, then ![]() $\pi (\overline {\rho })$ has an extra copy of
$\pi (\overline {\rho })$ has an extra copy of ![]() $\chi \circ \det$ than the representation
$\chi \circ \det$ than the representation ![]() $A_{r,\lambda }$. However, in this case
$A_{r,\lambda }$. However, in this case ![]() $(\chi \circ \det )|_K$ is not a Serre weight of
$(\chi \circ \det )|_K$ is not a Serre weight of ![]() $\overline {\rho }$. Thus, for any
$\overline {\rho }$. Thus, for any ![]() $\sigma \in W(\overline {\rho })$ the multiplicity of
$\sigma \in W(\overline {\rho })$ the multiplicity of ![]() $\sigma$ in
$\sigma$ in ![]() $\pi (\overline {\rho }) [\frak {m}_{K_1}^2]$ is equal to the multiplicity of
$\pi (\overline {\rho }) [\frak {m}_{K_1}^2]$ is equal to the multiplicity of ![]() $\sigma$ in
$\sigma$ in ![]() $A_{r,\lambda } [\frak {m}_{K_1}^2]$. The
$A_{r,\lambda } [\frak {m}_{K_1}^2]$. The ![]() $K$-socle filtration of
$K$-socle filtration of ![]() $A_{r,\lambda }$ is given by [Reference MorraMor17, Theorem 1.1] and [Reference MorraMor11, Theorem 1.2], from which the result follows.
$A_{r,\lambda }$ is given by [Reference MorraMor17, Theorem 1.1] and [Reference MorraMor11, Theorem 1.2], from which the result follows.
4.2.1 Results of Paškūnas
Recall that ![]() $\overline {\rho }$ is called generic in the sense of [Reference PaškūnasPaš15] if either
$\overline {\rho }$ is called generic in the sense of [Reference PaškūnasPaš15] if either ![]() $\overline {\rho }$ is absolutely irreducible or
$\overline {\rho }$ is absolutely irreducible or ![]() $\overline {\rho } \sim \big (\begin{smallmatrix} \chi _1 & * \\ 0 & \chi _2 \end{smallmatrix}\big )$ is reducible nonsplit with
$\overline {\rho } \sim \big (\begin{smallmatrix} \chi _1 & * \\ 0 & \chi _2 \end{smallmatrix}\big )$ is reducible nonsplit with ![]() $\chi _1 \chi _2^{-1} \neq \omega, \mathbf {1}$. We assume
$\chi _1 \chi _2^{-1} \neq \omega, \mathbf {1}$. We assume ![]() $\overline {\rho }$ is generic, so in particular
$\overline {\rho }$ is generic, so in particular ![]() $\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}} (\overline {\rho }) = \mathbb {F}$. Let
$\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}} (\overline {\rho }) = \mathbb {F}$. Let ![]() $\eta : G_{\mathbb {Q}_p} \to \mathcal {O}^{\times }$ be a character such that
$\eta : G_{\mathbb {Q}_p} \to \mathcal {O}^{\times }$ be a character such that ![]() $\eta \pmod {\varpi } = \det \overline {\rho }$. Let
$\eta \pmod {\varpi } = \det \overline {\rho }$. Let ![]() $R_{\overline {\rho }}^{\eta }$ denote the universal deformation ring of
$R_{\overline {\rho }}^{\eta }$ denote the universal deformation ring of ![]() $\overline {\rho }$ with determinant
$\overline {\rho }$ with determinant ![]() $\eta$ and let
$\eta$ and let ![]() $\rho ^{\rm univ}$ denote the universal object over
$\rho ^{\rm univ}$ denote the universal object over ![]() $R_{\overline {\rho }}^{\eta }$.
$R_{\overline {\rho }}^{\eta }$.
Let ![]() $\psi = \eta \varepsilon ^{-1}$. According to [Reference PaškūnasPaš15, § 6.1], there exists
$\psi = \eta \varepsilon ^{-1}$. According to [Reference PaškūnasPaš15, § 6.1], there exists ![]() $N \in \frak {C}_{G,\psi }(\mathcal {O})$ with a faithful continuous action of
$N \in \frak {C}_{G,\psi }(\mathcal {O})$ with a faithful continuous action of ![]() $R^{\eta }_{\overline {\rho }}$ which commutes with the action of
$R^{\eta }_{\overline {\rho }}$ which commutes with the action of ![]() $G$ such that:
$G$ such that:
(N0)
 $\mathbb {F}\widehat {\otimes }_{R_{\overline {\rho }}^{\eta }} N$ is of finite length in
$\mathbb {F}\widehat {\otimes }_{R_{\overline {\rho }}^{\eta }} N$ is of finite length in  $\frak {C}_{G,\psi }(\mathcal {O})$ and is finitely generated over
$\frak {C}_{G,\psi }(\mathcal {O})$ and is finitely generated over  $\mathcal {O}[\![ K ]\!];$
$\mathcal {O}[\![ K ]\!];$(N1)
 $\operatorname {{\mathrm {Hom}}}_{\mathrm {SL}_2(\mathbb {Q}_p)}(\mathbf {1}_G,N^{\vee })=0$;
$\operatorname {{\mathrm {Hom}}}_{\mathrm {SL}_2(\mathbb {Q}_p)}(\mathbf {1}_G,N^{\vee })=0$;(N2)
 $\operatorname {{\mathrm {End}}}_{\frak {C}_{G,\psi }(\mathcal {O})} (N) \cong R_{\overline {\rho }}^{\eta }$ and
$\operatorname {{\mathrm {End}}}_{\frak {C}_{G,\psi }(\mathcal {O})} (N) \cong R_{\overline {\rho }}^{\eta }$ and  $\check {\mathbf {V}}(N)$ is isomorphic to
$\check {\mathbf {V}}(N)$ is isomorphic to  $\rho ^{\rm univ}$ as
$\rho ^{\rm univ}$ as  $R_{\overline {\rho }}^{\eta }[\![ G_{\mathbb {Q}_p} ]\!]$-modules, where
$R_{\overline {\rho }}^{\eta }[\![ G_{\mathbb {Q}_p} ]\!]$-modules, where  $\check {\mathbf {V}}$ is the modified Colmez functor in [Reference PaškūnasPaš15, § 3];
$\check {\mathbf {V}}$ is the modified Colmez functor in [Reference PaškūnasPaš15, § 3];(N3)
 $N$ is projective in
$N$ is projective in  $\frak {C}_{G,\psi }(\mathcal {O})$, and there exists
$\frak {C}_{G,\psi }(\mathcal {O})$, and there exists  $x\in R^{\eta }_{\overline {\rho }}$ such that
$x\in R^{\eta }_{\overline {\rho }}$ such that  $N/xN$ is isomorphic to a projective envelope of
$N/xN$ is isomorphic to a projective envelope of  $\oplus _{\sigma \in W(\overline {\rho })}\sigma ^{\vee }$ in
$\oplus _{\sigma \in W(\overline {\rho })}\sigma ^{\vee }$ in  $\operatorname {\mathrm {Mod}}^{\rm pro}_{K ,\psi }(\mathcal {O})$.
$\operatorname {\mathrm {Mod}}^{\rm pro}_{K ,\psi }(\mathcal {O})$.
Remark 4.3 Under our assumption on ![]() $\overline {\rho }$,
$\overline {\rho }$, ![]() $N$ is just a projective envelope of
$N$ is just a projective envelope of ![]() $\mathbb {F}\widehat {\otimes }_{R_{\overline {\rho }}^{\eta }} N$ in
$\mathbb {F}\widehat {\otimes }_{R_{\overline {\rho }}^{\eta }} N$ in ![]() $\frak {C}_{G,\psi }(\mathcal {O})$. Hence, (N3) follows from [Reference PaškūnasPaš15, Theorem 5.2].
$\frak {C}_{G,\psi }(\mathcal {O})$. Hence, (N3) follows from [Reference PaškūnasPaš15, Theorem 5.2].
Proposition 4.4 Assume ![]() $\overline {\rho }$ is generic. Then there is an isomorphism
$\overline {\rho }$ is generic. Then there is an isomorphism ![]() $\mathbb {F}\widehat {\otimes }_{R_{\overline {\rho }}^{\eta }}N\cong \pi (\overline {\rho })^{\vee }$.
$\mathbb {F}\widehat {\otimes }_{R_{\overline {\rho }}^{\eta }}N\cong \pi (\overline {\rho })^{\vee }$.
Proof. See the proof of [Reference PaškūnasPaš15, Proposition 6.1].Footnote 4
If ![]() $\Theta$ (respectively,
$\Theta$ (respectively, ![]() $\sigma$) is a finite free
$\sigma$) is a finite free ![]() $\mathcal {O}$-module (respectively,
$\mathcal {O}$-module (respectively, ![]() $\mathbb {F}$-module) equipped with a continuous action of
$\mathbb {F}$-module) equipped with a continuous action of ![]() $K$, we define
$K$, we define
Then ![]() $M(\Theta )$ (respectively,
$M(\Theta )$ (respectively, ![]() $M(\sigma )$) is a finitely generated
$M(\sigma )$) is a finitely generated ![]() $R_{\overline {\rho }}^{\eta }$-module by (N0).
$R_{\overline {\rho }}^{\eta }$-module by (N0).
Let ![]() $\mathbf {w} = (a, b)$ be a pair of integers with
$\mathbf {w} = (a, b)$ be a pair of integers with ![]() $a< b$ and
$a< b$ and ![]() $\tau : I_{\mathbb {Q}_p} \to \mathrm {GL}_2(E)$ be an inertial type, where
$\tau : I_{\mathbb {Q}_p} \to \mathrm {GL}_2(E)$ be an inertial type, where ![]() $I_{\mathbb {Q}_p}$ is the inertia subgroup of
$I_{\mathbb {Q}_p}$ is the inertia subgroup of ![]() $G_{\mathbb {Q}_p}$. Let
$G_{\mathbb {Q}_p}$. Let
 \begin{gather*} \sigma(\mathbf{w},\tau):= \mathrm{Sym}^{b-a-1} E^2 \otimes {\det}^a\otimes \sigma(\tau),\\ \sigma^{\rm cr}(\mathbf{w},\tau):=\mathrm{Sym}^{b-a-1} E^2 \otimes {\det}^a\otimes \sigma^{\rm cr}(\tau), \end{gather*}
\begin{gather*} \sigma(\mathbf{w},\tau):= \mathrm{Sym}^{b-a-1} E^2 \otimes {\det}^a\otimes \sigma(\tau),\\ \sigma^{\rm cr}(\mathbf{w},\tau):=\mathrm{Sym}^{b-a-1} E^2 \otimes {\det}^a\otimes \sigma^{\rm cr}(\tau), \end{gather*}
where ![]() $\sigma (\tau )$ and
$\sigma (\tau )$ and ![]() $\sigma ^{\rm cr}(\tau )$ are finite-dimensional representations of
$\sigma ^{\rm cr}(\tau )$ are finite-dimensional representations of ![]() $K$ over
$K$ over ![]() $E$ associated to
$E$ associated to ![]() $\tau$ by the inertial local Langlands correspondence [Reference HenniartHen02] (see § 5.1 for details). Let
$\tau$ by the inertial local Langlands correspondence [Reference HenniartHen02] (see § 5.1 for details). Let ![]() $R^{\eta }_{\overline {\rho }}( \mathbf {w},\tau )$ (respectively,
$R^{\eta }_{\overline {\rho }}( \mathbf {w},\tau )$ (respectively, ![]() $R^{\eta,{\rm cr}}_{\overline {\rho }}(\mathbf {w}, \tau )$) denote the reduced
$R^{\eta,{\rm cr}}_{\overline {\rho }}(\mathbf {w}, \tau )$) denote the reduced ![]() $p$-torsion-free quotient of
$p$-torsion-free quotient of ![]() $R_{\overline {\rho }}^{\eta }$ which parametrizes potentially semistable (respectively, potentially crystalline) deformations of
$R_{\overline {\rho }}^{\eta }$ which parametrizes potentially semistable (respectively, potentially crystalline) deformations of ![]() $\overline {\rho }$ of Hodge–Tate weights
$\overline {\rho }$ of Hodge–Tate weights ![]() $\mathbf {w}$ and type
$\mathbf {w}$ and type ![]() $\tau$. It is well-known that these rings are nonzero only if
$\tau$. It is well-known that these rings are nonzero only if ![]() $\eta \varepsilon ^{-(a+b)}|_{I_{\mathbb {Q}_p}}\sim \det \tau$, in which case they have Krull dimension
$\eta \varepsilon ^{-(a+b)}|_{I_{\mathbb {Q}_p}}\sim \det \tau$, in which case they have Krull dimension ![]() $2$. This requires, in particular, that
$2$. This requires, in particular, that ![]() $\eta$ is locally algebraic.
$\eta$ is locally algebraic.
Recall the following theorem of Paškūnas.
Theorem 4.5 Let ![]() $\mathbf {w}, \tau$ be as above. Let
$\mathbf {w}, \tau$ be as above. Let ![]() $\Theta$ be any
$\Theta$ be any ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $\sigma (\mathbf {w},\tau )$ (respectively,
$\sigma (\mathbf {w},\tau )$ (respectively, ![]() $\sigma ^{\rm cr}(\mathbf {w},\tau )$). Then
$\sigma ^{\rm cr}(\mathbf {w},\tau )$). Then ![]() $R_{\overline {\rho }}^{\eta } /\operatorname {{\mathrm {Ann}}}_{R^{\eta }_{\overline {\rho }}}( M (\Theta ))$ is equal to
$R_{\overline {\rho }}^{\eta } /\operatorname {{\mathrm {Ann}}}_{R^{\eta }_{\overline {\rho }}}( M (\Theta ))$ is equal to ![]() $R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$ (respectively,
$R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$ (respectively, ![]() $R_{\overline {\rho }}^{\eta,{\rm cr}}(\mathbf {w}, \tau )$).
$R_{\overline {\rho }}^{\eta,{\rm cr}}(\mathbf {w}, \tau )$).
Proof. See [Reference PaškūnasPaš15, Corollary 6.5].
Let ![]() $\delta :G_{\mathbb {Q}_p}\rightarrow \mathcal {O}^{\times }$ be a continuous character that is trivial modulo
$\delta :G_{\mathbb {Q}_p}\rightarrow \mathcal {O}^{\times }$ be a continuous character that is trivial modulo ![]() $p$, not necessarily locally algebraic. Twisting by
$p$, not necessarily locally algebraic. Twisting by ![]() $\delta$ induces a natural isomorphism of
$\delta$ induces a natural isomorphism of ![]() $\mathcal {O}$-algebras
$\mathcal {O}$-algebras
By a similar discussion as in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, § 6.1], we have the following variant of Theorem 4.5.
Corollary 4.6 Assume ![]() $\eta \delta ^2\varepsilon ^{-(a+b)}|_{I_{\mathbb {Q}_p}}\sim \det \tau$. Let
$\eta \delta ^2\varepsilon ^{-(a+b)}|_{I_{\mathbb {Q}_p}}\sim \det \tau$. Let ![]() $\Theta$ be any
$\Theta$ be any ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $\sigma (\mathbf {w},\tau )\otimes \delta ^{-1}\circ \det$ (respectively,
$\sigma (\mathbf {w},\tau )\otimes \delta ^{-1}\circ \det$ (respectively, ![]() $\sigma ^{\rm cr}(\mathbf {w},\tau )\otimes \delta ^{-1}\circ \det$). Then
$\sigma ^{\rm cr}(\mathbf {w},\tau )\otimes \delta ^{-1}\circ \det$). Then ![]() $R_{\overline {\rho }}^{\eta }/\mathrm {Ann}_{R_{\overline {\rho }}^{\eta }}(M(\Theta ))$ is equal to
$R_{\overline {\rho }}^{\eta }/\mathrm {Ann}_{R_{\overline {\rho }}^{\eta }}(M(\Theta ))$ is equal to ![]() $\mathrm {tw}_{\delta }(R_{\overline {\rho }}^{\eta \delta ^2}(\mathbf {w},\tau ))$ (respectively,
$\mathrm {tw}_{\delta }(R_{\overline {\rho }}^{\eta \delta ^2}(\mathbf {w},\tau ))$ (respectively, ![]() $\mathrm {tw}_{\delta }(R_{\overline {\rho }}^{\eta \delta ^2, {\rm cr}}(\mathbf {w},\tau ))$). As a consequence, we have isomorphisms of
$\mathrm {tw}_{\delta }(R_{\overline {\rho }}^{\eta \delta ^2, {\rm cr}}(\mathbf {w},\tau ))$). As a consequence, we have isomorphisms of ![]() $\mathcal {O}$-algebras
$\mathcal {O}$-algebras
(respectively, for ![]() $R_{\overline {\rho }}^{\eta \delta ^2,{\rm cr}}(\mathbf {w},\tau )$).
$R_{\overline {\rho }}^{\eta \delta ^2,{\rm cr}}(\mathbf {w},\tau )$).
If ![]() $\sigma$ is a finite-dimensional
$\sigma$ is a finite-dimensional ![]() $\mathbb {F}[K]$-module, by Proposition 4.4 we have
$\mathbb {F}[K]$-module, by Proposition 4.4 we have
It follows from (N3) and Nakayama's lemma that ![]() $M(\sigma )\neq 0$ if and only if
$M(\sigma )\neq 0$ if and only if ![]() $\sigma$ admits at least one Jordan–Hölder factor lying in
$\sigma$ admits at least one Jordan–Hölder factor lying in ![]() $W(\overline {\rho })$.
$W(\overline {\rho })$.
4.2.2 A criterion for regularity
Lemma 4.7 Let ![]() $\sigma \in \operatorname {\mathrm {Mod}}_{K}^{\rm sm}(\mathbb {F})$ be of finite length. Assume that, taking into account multiplicities,
$\sigma \in \operatorname {\mathrm {Mod}}_{K}^{\rm sm}(\mathbb {F})$ be of finite length. Assume that, taking into account multiplicities, ![]() $\operatorname {{\mathrm {JH}}}(\sigma )$ contains exactly one element in
$\operatorname {{\mathrm {JH}}}(\sigma )$ contains exactly one element in ![]() $W(\overline {\rho })$. Then
$W(\overline {\rho })$. Then ![]() $M(\sigma )$ is a cyclic
$M(\sigma )$ is a cyclic ![]() $R_{\overline {\rho }}^{\eta }$-module and isomorphic to
$R_{\overline {\rho }}^{\eta }$-module and isomorphic to ![]() $\mathbb {F}[\![x]\!]$, where
$\mathbb {F}[\![x]\!]$, where ![]() $x\in R_{\overline {\rho }}^{\eta }$ is as in (N3).
$x\in R_{\overline {\rho }}^{\eta }$ is as in (N3).
Proof. See (the end of) the proof of [Reference PaškūnasPaš15, Theorem 6.6].
Recall that ![]() $\mathcal {O}$ is unramified over
$\mathcal {O}$ is unramified over ![]() $\mathbb {Z}_p$.
$\mathbb {Z}_p$.
Proposition 4.8 Let ![]() $\mathbf {w}, \tau$ be as above. Assume that there exist two
$\mathbf {w}, \tau$ be as above. Assume that there exist two ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattices
$\mathcal {O}$-lattices ![]() $\Theta _1, \Theta _2$ in
$\Theta _1, \Theta _2$ in ![]() $\sigma (\mathbf {w},\tau )$ (respectively,
$\sigma (\mathbf {w},\tau )$ (respectively, ![]() $\sigma ^{\rm cr}(\mathbf {w},\tau )$) such that the following conditions hold:
$\sigma ^{\rm cr}(\mathbf {w},\tau )$) such that the following conditions hold:
(a)
 $p\Theta _1\subset \Theta _2\subset \Theta _1$ and
$p\Theta _1\subset \Theta _2\subset \Theta _1$ and  $\dim _{\mathbb {F}}\operatorname {{\mathrm {Hom}}}_{K}(\Theta _i/p\Theta _i,\pi (\overline {\rho }))=1$ for
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Hom}}}_{K}(\Theta _i/p\Theta _i,\pi (\overline {\rho }))=1$ for  $i=1,2$;
$i=1,2$;(b) taking into account multiplicities,
 $\operatorname {{\mathrm {JH}}}(\Theta _1/\Theta _2)$ contains exactly one element in
$\operatorname {{\mathrm {JH}}}(\Theta _1/\Theta _2)$ contains exactly one element in  $W(\overline {\rho })$.
$W(\overline {\rho })$.
Then ![]() $R^{\eta }_{\overline {\rho }}(\mathbf {w},\tau )$ (respectively,
$R^{\eta }_{\overline {\rho }}(\mathbf {w},\tau )$ (respectively, ![]() $R_{\overline {\rho }}^{\eta,{\rm cr}}(\mathbf {w},\tau )$) is a regular local ring.
$R_{\overline {\rho }}^{\eta,{\rm cr}}(\mathbf {w},\tau )$) is a regular local ring.
Proof. We only treat the case for ![]() $R^{\eta }_{\overline {\rho }}(\mathbf {w},\tau )$. By Nakayama's lemma and (4.3), condition (a) implies that
$R^{\eta }_{\overline {\rho }}(\mathbf {w},\tau )$. By Nakayama's lemma and (4.3), condition (a) implies that ![]() $M(\Theta _1)$ and
$M(\Theta _1)$ and ![]() $M(\Theta _2)$ are both cyclic modules over
$M(\Theta _2)$ are both cyclic modules over ![]() $R_{\overline {\rho }}^{\eta }$. Hence,
$R_{\overline {\rho }}^{\eta }$. Hence, ![]() $M(\Theta _1)$ and
$M(\Theta _1)$ and ![]() $M(\Theta _2)$ are isomorphic to
$M(\Theta _2)$ are isomorphic to ![]() $R^{\eta }_{\overline {\rho }}(\mathbf {w},\tau )$ by Theorem 4.5.
$R^{\eta }_{\overline {\rho }}(\mathbf {w},\tau )$ by Theorem 4.5.
The exact sequence ![]() $0\rightarrow \Theta _2\rightarrow \Theta _1\rightarrow \Theta _1/\Theta _2\rightarrow 0$ induces a sequence of
$0\rightarrow \Theta _2\rightarrow \Theta _1\rightarrow \Theta _1/\Theta _2\rightarrow 0$ induces a sequence of ![]() $R_{\overline {\rho }}^{\eta }$-modules
$R_{\overline {\rho }}^{\eta }$-modules
which is again exact by (N3). Since both ![]() $M(\Theta _1)$ and
$M(\Theta _1)$ and ![]() $M(\Theta _2)$ are isomorphic to
$M(\Theta _2)$ are isomorphic to ![]() $R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$, the morphism
$R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$, the morphism ![]() $f$ is equal to the multiplication by some element
$f$ is equal to the multiplication by some element ![]() $y\in R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$. On the other hand, by Lemma 4.7, condition (b) implies that
$y\in R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$. On the other hand, by Lemma 4.7, condition (b) implies that ![]() $M(\Theta _1/\Theta _2)$ is isomorphic to
$M(\Theta _1/\Theta _2)$ is isomorphic to ![]() $\mathbb {F}[\![x]\!]$. This means that
$\mathbb {F}[\![x]\!]$. This means that ![]() $R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )/(y)$ is a regular local ring of Krull dimension
$R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )/(y)$ is a regular local ring of Krull dimension ![]() $1$. Since
$1$. Since ![]() $R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$ has Krull dimension
$R_{\overline {\rho }}^{\eta }(\mathbf {w},\tau )$ has Krull dimension ![]() $2$, it is also regular.
$2$, it is also regular.
4.3 Potentially crystalline deformation rings of tame supercuspidal inertial types
In this subsection, we assume ![]() $\overline {\rho }$ is of one of the following forms:
$\overline {\rho }$ is of one of the following forms:
(C1)
 $\overline {\rho }$ is in case 1 of § 4.1.1 with
$\overline {\rho }$ is in case 1 of § 4.1.1 with  $2 \leq r\leq p-3;$
$2 \leq r\leq p-3;$(C2)
 $\overline {\rho }$ is in case 2 of § 4.1.1 with
$\overline {\rho }$ is in case 2 of § 4.1.1 with  $1 \leq r\leq p-3$.
$1 \leq r\leq p-3$.
In particular, ![]() $\overline {\rho }$ is generic (see § 4.2.1). We study the properties of deformation rings of tame supercuspidal inertial types and Hodge–Tate weights
$\overline {\rho }$ is generic (see § 4.2.1). We study the properties of deformation rings of tame supercuspidal inertial types and Hodge–Tate weights ![]() $(0,1)$ and
$(0,1)$ and ![]() $(0,2)$ in the cases (C1) and (C2) separately. The main result is Theorem 4.15.
$(0,2)$ in the cases (C1) and (C2) separately. The main result is Theorem 4.15.
Recall that given a pair of integers ![]() $(a,b)$ with
$(a,b)$ with ![]() $1\leq a \leq p-3$, we can associate:
$1\leq a \leq p-3$, we can associate:
• characters
 $\psi _i$,
$\psi _i$,  $1 \leq i \leq 3$, introduced in (3.15);
$1 \leq i \leq 3$, introduced in (3.15);• tame supercuspidal inertial types
 $\tau _i=\psi _i\oplus \psi _i^p$ satisfying
$\tau _i=\psi _i\oplus \psi _i^p$ satisfying  $\sigma (\tau _i) = \Theta (\psi _i)$ (cf. Lemma 5.1);
$\sigma (\tau _i) = \Theta (\psi _i)$ (cf. Lemma 5.1);• lattices
 $R_1, R_2, R_3, R , \widetilde {R}$ introduced in § 3.4 satisfying
$R_1, R_2, R_3, R , \widetilde {R}$ introduced in § 3.4 satisfying  ${\rm cosoc}(\mathcal {R} / p \mathcal {R}) = \sigma _{a,b+1}$ for any
${\rm cosoc}(\mathcal {R} / p \mathcal {R}) = \sigma _{a,b+1}$ for any  $\mathcal {R} \in \{R_1, R_2, R_3, R, \widetilde {R}\}$.
$\mathcal {R} \in \{R_1, R_2, R_3, R, \widetilde {R}\}$.
We choose ![]() $(a,b)$ as follows:
$(a,b)$ as follows:
• in the case (C1), let
 $(a, b) \in \{(r,s), (p-1-r, r+s)\};$
$(a, b) \in \{(r,s), (p-1-r, r+s)\};$• in the case (C2), let
 $(a,b) = (r,s)$.
$(a,b) = (r,s)$.
Then ![]() $\sigma _{a,b+1}$ lies in
$\sigma _{a,b+1}$ lies in ![]() $W(\overline {\rho })$ by Theorem 4.1. For
$W(\overline {\rho })$ by Theorem 4.1. For ![]() $\mathcal {R} \in \{R_1, R_2, R_3, R , \widetilde {R}\}$, we denote by
$\mathcal {R} \in \{R_1, R_2, R_3, R , \widetilde {R}\}$, we denote by
the annihilator of ![]() $M(\mathcal {R})$ in
$M(\mathcal {R})$ in ![]() $R_{\overline {\rho }}^{\eta }$.
$R_{\overline {\rho }}^{\eta }$.
Proposition 4.9 We have that ![]() $M(\mathcal {R})$ is a (nonzero) cyclic
$M(\mathcal {R})$ is a (nonzero) cyclic ![]() $R_{\overline {\rho }}^{\eta }$-module for
$R_{\overline {\rho }}^{\eta }$-module for ![]() $\mathcal {R} \in \{R_1,R_2,R_3,$
$\mathcal {R} \in \{R_1,R_2,R_3,$ ![]() $R,\widetilde {R}\}$. As a consequence
$R,\widetilde {R}\}$. As a consequence ![]() $M(\mathcal {R}) \cong R_{\overline {\rho }}^{\eta } / I_{\mathcal {R}}$.
$M(\mathcal {R}) \cong R_{\overline {\rho }}^{\eta } / I_{\mathcal {R}}$.
Proof. By Nakayama's lemma, it suffices to show ![]() $M(\mathcal {R})/\frak {m}$ is of dimension
$M(\mathcal {R})/\frak {m}$ is of dimension ![]() $1$ over
$1$ over ![]() $\mathbb {F}$, where
$\mathbb {F}$, where ![]() $\frak {m}$ denotes the maximal ideal of
$\frak {m}$ denotes the maximal ideal of ![]() $R_{\overline {\rho }}^{\eta }$. Since
$R_{\overline {\rho }}^{\eta }$. Since ![]() $\sigma _{a,b+1}\in W(\overline {\rho })$ is a quotient of
$\sigma _{a,b+1}\in W(\overline {\rho })$ is a quotient of ![]() $\mathcal {R}/p\mathcal {R}$, we always have
$\mathcal {R}/p\mathcal {R}$, we always have ![]() $\dim _{\mathbb {F}} M(\mathcal {R}/p\mathcal {R})/ \mathfrak {m} \geq 1$ by (N3) of § 4.2.1.
$\dim _{\mathbb {F}} M(\mathcal {R}/p\mathcal {R})/ \mathfrak {m} \geq 1$ by (N3) of § 4.2.1.
To show ![]() $\dim _{\mathbb {F}} M(\mathcal {R}/p\mathcal {R})/ \mathfrak {m} \leq 1$, we note that
$\dim _{\mathbb {F}} M(\mathcal {R}/p\mathcal {R})/ \mathfrak {m} \leq 1$, we note that ![]() $\mathcal {R}/p\mathcal {R}$ is a quotient of
$\mathcal {R}/p\mathcal {R}$ is a quotient of ![]() $(\operatorname {{\mathrm {Proj}}}_{\mathbb {F}[\![K / Z_1]\!]} \sigma _{a, b+1}) /\frak {m}_{K_1}^2$ by Lemma 3.18, Corollary 3.23 and Proposition 3.24. Hence, by (N3) of § 4.2.1
$(\operatorname {{\mathrm {Proj}}}_{\mathbb {F}[\![K / Z_1]\!]} \sigma _{a, b+1}) /\frak {m}_{K_1}^2$ by Lemma 3.18, Corollary 3.23 and Proposition 3.24. Hence, by (N3) of § 4.2.1
If ![]() $\overline {\rho }$ satisfies either case (C1) or case (C2), then by (4.3) and Theorem 4.2, we have
$\overline {\rho }$ satisfies either case (C1) or case (C2), then by (4.3) and Theorem 4.2, we have
Hence, ![]() $\dim _{\mathbb {F}} M (\mathcal {R}/ p\mathcal {R} )/\frak {m} = 1$.
$\dim _{\mathbb {F}} M (\mathcal {R}/ p\mathcal {R} )/\frak {m} = 1$.
Remark 4.10 For ![]() $i\in \{2,3\}$, we have constructed
$i\in \{2,3\}$, we have constructed ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattices
$\mathcal {O}$-lattices ![]() $L, L'$ in
$L, L'$ in ![]() $\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _i)$ in Proposition 3.11. The cosocle of
$\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _i)$ in Proposition 3.11. The cosocle of ![]() $L/pL$ (respectively,
$L/pL$ (respectively, ![]() $L'/pL'$) need not be irreducible, but
$L'/pL'$) need not be irreducible, but ![]() $M(L)$ (respectively,
$M(L)$ (respectively, ![]() $M(L')$) is still cyclic over
$M(L')$) is still cyclic over ![]() $R_{\overline {\rho }}^{\eta }$.
$R_{\overline {\rho }}^{\eta }$.
Indeed, if ![]() $\operatorname {{\mathrm {JH}}}(\overline {\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _i)}^{\rm ss})\cap W(\overline {\rho })$ consists of one element, then the claim is obvious. Otherwise,
$\operatorname {{\mathrm {JH}}}(\overline {\underline {\mathrm {Sym}}^1E^2\otimes \Theta (\psi _i)}^{\rm ss})\cap W(\overline {\rho })$ consists of one element, then the claim is obvious. Otherwise, ![]() $\overline {\rho }$ satisfies case (C1) and
$\overline {\rho }$ satisfies case (C1) and ![]() $W(\overline {\rho })$ consists of two elements, say
$W(\overline {\rho })$ consists of two elements, say ![]() $W(\overline {\rho })=\{\sigma _1,\sigma _2\} \subset \operatorname {{\mathrm {JH}}}(\overline {\underline {\mathrm {Sym}}^{1}E^2\otimes \Theta (\psi _i)}^{\rm ss})$. By Proposition 3.11, one of the nonsplit extensions,
$W(\overline {\rho })=\{\sigma _1,\sigma _2\} \subset \operatorname {{\mathrm {JH}}}(\overline {\underline {\mathrm {Sym}}^{1}E^2\otimes \Theta (\psi _i)}^{\rm ss})$. By Proposition 3.11, one of the nonsplit extensions, ![]() $E=(\sigma _1\ \textbf {---}\ \sigma _2)$ or
$E=(\sigma _1\ \textbf {---}\ \sigma _2)$ or ![]() $E'=(\sigma _2\ \textbf {---}\ \sigma _1)$, occurs in
$E'=(\sigma _2\ \textbf {---}\ \sigma _1)$, occurs in ![]() $L/pL$ (respectively,
$L/pL$ (respectively, ![]() $L'/pL'$). As in the proof of Proposition 4.9,
$L'/pL'$). As in the proof of Proposition 4.9, ![]() $M(E)$ and
$M(E)$ and ![]() $M(E')$ are cyclic over
$M(E')$ are cyclic over ![]() $R_{\overline {\rho }}^{\eta }$, from which the claim follows as
$R_{\overline {\rho }}^{\eta }$, from which the claim follows as ![]() $M(\sigma )=0$ for
$M(\sigma )=0$ for ![]() $\sigma \notin W(\overline {\rho })$.
$\sigma \notin W(\overline {\rho })$.
Corollary 4.11 We have:
(i)
 $I_{R_1} + I_{R_2} = (p, I_{R_1})$ and
$I_{R_1} + I_{R_2} = (p, I_{R_1})$ and  $I_R = I_{R_1} \cap I_{R_2}$;
$I_R = I_{R_1} \cap I_{R_2}$;(ii)
 $I_{R} + I_{R_3} = (p, I_{R_1})$ and
$I_{R} + I_{R_3} = (p, I_{R_1})$ and  $I_{\widetilde {R}} = I_{R_1}\cap I_{R_2} \cap I_{R_3}$.
$I_{\widetilde {R}} = I_{R_1}\cap I_{R_2} \cap I_{R_3}$.
Proof. Recall the following lemma from [Reference Hu and WangHW22, Lemma 8.11].
Lemma 4.12 Let ![]() $(A,\mathfrak {m}_A)$ be a commutative noetherian local ring with
$(A,\mathfrak {m}_A)$ be a commutative noetherian local ring with ![]() $k=A/\mathfrak {m}_A$. Let
$k=A/\mathfrak {m}_A$. Let ![]() $\mathcal {I}_0, \mathcal {I}_1,\mathcal {I}_2$ be ideals of
$\mathcal {I}_0, \mathcal {I}_1,\mathcal {I}_2$ be ideals of ![]() $A$ such that
$A$ such that ![]() $\mathcal {I}_1,\mathcal {I}_2\subset \mathcal {I}_0\subset \mathfrak {m}_A$. Consider the natural surjective homomorphism
$\mathcal {I}_1,\mathcal {I}_2\subset \mathcal {I}_0\subset \mathfrak {m}_A$. Consider the natural surjective homomorphism ![]() $A/\mathcal {I}_1\oplus A/\mathcal {I}_2\twoheadrightarrow A/\mathcal {I}_0$. Then
$A/\mathcal {I}_1\oplus A/\mathcal {I}_2\twoheadrightarrow A/\mathcal {I}_0$. Then ![]() $\operatorname {{\mathrm {Ker}}}(A/\mathcal {I}_1\oplus A/\mathcal {I}_2\twoheadrightarrow A/\mathcal {I}_0)$ is a cyclic
$\operatorname {{\mathrm {Ker}}}(A/\mathcal {I}_1\oplus A/\mathcal {I}_2\twoheadrightarrow A/\mathcal {I}_0)$ is a cyclic ![]() $A$-module if and only if
$A$-module if and only if ![]() $\mathcal {I}_1+\mathcal {I}_2=\mathcal {I}_0$.
$\mathcal {I}_1+\mathcal {I}_2=\mathcal {I}_0$.
By (N3), the sequence (3.20) induces a short exact sequence
Since ![]() $M(R)$ is cyclic over
$M(R)$ is cyclic over ![]() $R_{\overline {\rho }}^{\eta }$ by Proposition 4.9, we deduce part (i) using Lemma 4.12 and the fact thatFootnote 5
$R_{\overline {\rho }}^{\eta }$ by Proposition 4.9, we deduce part (i) using Lemma 4.12 and the fact thatFootnote 5
Similarly, we obtain part (ii) by using the short exact sequence (3.22).
Let ![]() $\delta :G_{\mathbb {Q}_p}\rightarrow \mathcal {O}^{\times }$ denote the character, via the local class field theory, sending
$\delta :G_{\mathbb {Q}_p}\rightarrow \mathcal {O}^{\times }$ denote the character, via the local class field theory, sending ![]() $x\in \mathbb {Q}_p^{\times }\mapsto \mathrm {pr}(x)^{1/2}\in 1+p\mathbb {Z}_p$. By Theorem 4.5 and Corollary 4.6, we have
$x\in \mathbb {Q}_p^{\times }\mapsto \mathrm {pr}(x)^{1/2}\in 1+p\mathbb {Z}_p$. By Theorem 4.5 and Corollary 4.6, we have
Proposition 4.13 The ring ![]() $R_{\overline {\rho }}^{\eta }((0,1), \tau _1)$ is a regular local ring.
$R_{\overline {\rho }}^{\eta }((0,1), \tau _1)$ is a regular local ring.
Proof. Recall from § 3.3 that there exist two ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattices
$\mathcal {O}$-lattices ![]() $T,T'\subset \sigma (\tau _1)$ such that
$T,T'\subset \sigma (\tau _1)$ such that ![]() $pT\subset T'\subset T$ and
$pT\subset T'\subset T$ and ![]() $T/T'\cong \sigma _{a,b+1}$ and
$T/T'\cong \sigma _{a,b+1}$ and ![]() $\mathrm {cosoc}(T/pT)\cong \sigma _{a,b+1}$. Here, if
$\mathrm {cosoc}(T/pT)\cong \sigma _{a,b+1}$. Here, if ![]() $\operatorname {{\mathrm {JH}}} (\overline {\sigma (\tau _1)}^{\rm ss})\cap W(\overline {\rho })$ consists of only one element, then we take
$\operatorname {{\mathrm {JH}}} (\overline {\sigma (\tau _1)}^{\rm ss})\cap W(\overline {\rho })$ consists of only one element, then we take ![]() $T'=pT$. In any case, the cosocle of
$T'=pT$. In any case, the cosocle of ![]() $T'/pT'$ is irreducible. Using Theorem 4.2, it is easy to check that
$T'/pT'$ is irreducible. Using Theorem 4.2, it is easy to check that
The result then follows from Proposition 4.8.
Remark 4.14 If ![]() $\overline {\rho }$ is generic in the sense of [Reference Breuil and PaškūnasBP12, Definition 11.7], Proposition 4.13 is a direct consequence of [Reference Emerton, Gee and SavittEGS15, Theorem 7.2.1].
$\overline {\rho }$ is generic in the sense of [Reference Breuil and PaškūnasBP12, Definition 11.7], Proposition 4.13 is a direct consequence of [Reference Emerton, Gee and SavittEGS15, Theorem 7.2.1].
Theorem 4.15 The rings ![]() $R_{\overline {\rho }}^{\eta \delta ^2}((0,2),\tau _2)$ and
$R_{\overline {\rho }}^{\eta \delta ^2}((0,2),\tau _2)$ and ![]() $R_{\overline {\rho }}^{\eta \delta ^2}((0,2),\tau _3)$ are regular local rings.
$R_{\overline {\rho }}^{\eta \delta ^2}((0,2),\tau _3)$ are regular local rings.
Proof. Assume ![]() $\overline {\rho }$ is in case (C1). For
$\overline {\rho }$ is in case (C1). For ![]() $R_{\overline {\rho }}^{\eta \delta ^2 }((0,2),\tau _2)$, it is equivalent to proving that
$R_{\overline {\rho }}^{\eta \delta ^2 }((0,2),\tau _2)$, it is equivalent to proving that ![]() $R^{\eta }_{\overline {\rho }}/I_{R_2}$ is a regular local ring by (4.5). Note that
$R^{\eta }_{\overline {\rho }}/I_{R_2}$ is a regular local ring by (4.5). Note that ![]() $\sigma _{a,b+1}$ is the unique Serre weight in the intersection
$\sigma _{a,b+1}$ is the unique Serre weight in the intersection ![]() $\operatorname {{\mathrm {JH}}} (\overline {\underline {\mathrm {Sym}}^1E^2 \otimes \sigma (\tau _2)}^{\rm ss}) \cap W(\overline {\rho })$. The assertion follows from Proposition 4.8, by choosing any
$\operatorname {{\mathrm {JH}}} (\overline {\underline {\mathrm {Sym}}^1E^2 \otimes \sigma (\tau _2)}^{\rm ss}) \cap W(\overline {\rho })$. The assertion follows from Proposition 4.8, by choosing any ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice
$\mathcal {O}$-lattice ![]() $\Theta _1$ in
$\Theta _1$ in ![]() $\underline {\mathrm {Sym}}^1E^2\otimes \sigma (\tau _2)$, and taking
$\underline {\mathrm {Sym}}^1E^2\otimes \sigma (\tau _2)$, and taking ![]() $\Theta _2=p\Theta _1$ in Proposition 4.8.
$\Theta _2=p\Theta _1$ in Proposition 4.8.
We now consider ![]() $R_{\overline {\rho }}^{\eta \delta ^2}((0,2),\tau _3)$, equivalently
$R_{\overline {\rho }}^{\eta \delta ^2}((0,2),\tau _3)$, equivalently ![]() $R_{\overline {\rho }}^{\eta }/I_{R_3}$ via (4.5). By Proposition 3.11, there are
$R_{\overline {\rho }}^{\eta }/I_{R_3}$ via (4.5). By Proposition 3.11, there are ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattices
$\mathcal {O}$-lattices ![]() $L,L'$ of
$L,L'$ of ![]() $\underline {\mathrm {Sym}}^1 E^2\otimes \Theta (\psi _3)$ such that
$\underline {\mathrm {Sym}}^1 E^2\otimes \Theta (\psi _3)$ such that ![]() $pL \subset L' \subset L$ and
$pL \subset L' \subset L$ and
Note that ![]() $\sigma _{a-2,b+2}\notin W(\overline {\rho })$. Using Remark 4.10, the result follows from Proposition 4.8.
$\sigma _{a-2,b+2}\notin W(\overline {\rho })$. Using Remark 4.10, the result follows from Proposition 4.8.
Assume ![]() $\overline {\rho }$ is in case (C2). Then
$\overline {\rho }$ is in case (C2). Then ![]() $\overline {\rho }$ has only one Serre weight
$\overline {\rho }$ has only one Serre weight ![]() $\sigma _{a,b+1}$, and we conclude as in the first paragraph.
$\sigma _{a,b+1}$, and we conclude as in the first paragraph.
4.4 Endomorphism rings and faithfulness
In this subsection, we assume ![]() $\overline {\rho }$ is reducible nonsplit and isomorphic to
$\overline {\rho }$ is reducible nonsplit and isomorphic to ![]() $\big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$. Let
$\big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$. Let ![]() $N\in \mathfrak {C}_{G/Z_G}(\mathcal {O})$ be as in § 4.2.1. In this case
$N\in \mathfrak {C}_{G/Z_G}(\mathcal {O})$ be as in § 4.2.1. In this case ![]() $N$ is isomorphic to a projective envelope of
$N$ is isomorphic to a projective envelope of ![]() $(\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^{G}\omega \otimes \omega ^{-1})^{\vee }$ in
$(\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^{G}\omega \otimes \omega ^{-1})^{\vee }$ in ![]() $\mathfrak {C}_{G/Z_G}(\mathcal {O})$.
$\mathfrak {C}_{G/Z_G}(\mathcal {O})$.
Let ![]() $(A,\mathfrak {m}_A)$ be a pseudo-compact flat local
$(A,\mathfrak {m}_A)$ be a pseudo-compact flat local ![]() $\mathcal {O}$-algebra with residue field
$\mathcal {O}$-algebra with residue field ![]() $\mathbb {F}$. Set
$\mathbb {F}$. Set ![]() $R:=A\widehat {\otimes }_{\mathcal {O}}R_{\overline {\rho }}^{\eta }$ and
$R:=A\widehat {\otimes }_{\mathcal {O}}R_{\overline {\rho }}^{\eta }$ and
Then ![]() $M\in \frak {C}_{G/Z_G}(R)$. In fact, as in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, Lemma 4.9] we show that
$M\in \frak {C}_{G/Z_G}(R)$. In fact, as in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, Lemma 4.9] we show that ![]() $M^{\vee }$ is admissible in
$M^{\vee }$ is admissible in ![]() $\operatorname {\mathrm {Mod}}_G^{\rm sm}(R)$, and so
$\operatorname {\mathrm {Mod}}_G^{\rm sm}(R)$, and so ![]() $M\in \mathfrak {C}_{G/Z_G}(\mathcal {O})$.
$M\in \mathfrak {C}_{G/Z_G}(\mathcal {O})$.
Lemma 4.16 The object ![]() $M$ is a projective object in
$M$ is a projective object in ![]() $\mathfrak {C}_{G/Z_G}(\mathcal {O})$.
$\mathfrak {C}_{G/Z_G}(\mathcal {O})$.
Proof. By assumption ![]() $A$ is
$A$ is ![]() $\mathcal {O}$-flat. Since pseudo-compact flat
$\mathcal {O}$-flat. Since pseudo-compact flat ![]() $\mathcal {O}$-modules are projective (see, e.g., [Reference BrumerBru66, Proposition 3.1]),
$\mathcal {O}$-modules are projective (see, e.g., [Reference BrumerBru66, Proposition 3.1]), ![]() $A$ is a projective
$A$ is a projective ![]() $\mathcal {O}$-module. By the definition of
$\mathcal {O}$-module. By the definition of ![]() $M$ we have
$M$ we have
from which the result follows.
Lemma 4.17 We have ![]() $\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,\mathbf {1}_G^{\vee })=0$ and
$\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,\mathbf {1}_G^{\vee })=0$ and ![]() $\operatorname {{\mathrm {Ext}}}^1_{\frak {C}_{G/Z_G}(R)}(M,\mathbf {1}_G^{\vee })=0$.
$\operatorname {{\mathrm {Ext}}}^1_{\frak {C}_{G/Z_G}(R)}(M,\mathbf {1}_G^{\vee })=0$.
Proof. The first assertion follows from (4.6) because ![]() $\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(\mathcal {O})}(N,\mathbf {1}_G^{\vee })=0$, see (N1) in § 4.2.1. For the second, we work on the dual side and show
$\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(\mathcal {O})}(N,\mathbf {1}_G^{\vee })=0$, see (N1) in § 4.2.1. For the second, we work on the dual side and show ![]() $\operatorname {{\mathrm {Ext}}}^1_{R[G]}(\mathbf {1}_G,M^{\vee })=0$. By Lemma 4.16,
$\operatorname {{\mathrm {Ext}}}^1_{R[G]}(\mathbf {1}_G,M^{\vee })=0$. By Lemma 4.16, ![]() $M$ is a projective object in
$M$ is a projective object in ![]() $\frak {C}_{G/Z_G}(\mathcal {O})$, so dually
$\frak {C}_{G/Z_G}(\mathcal {O})$, so dually ![]() $M^{\vee }$ is an injective object in
$M^{\vee }$ is an injective object in ![]() $\operatorname {\mathrm {Mod}}_{G/Z_G}^{\rm l.adm}(\mathcal {O})$. Consider an extension
$\operatorname {\mathrm {Mod}}_{G/Z_G}^{\rm l.adm}(\mathcal {O})$. Consider an extension
in ![]() $\operatorname {\mathrm {Mod}}_{G/Z_G}^{\rm l.adm}(R)$. It must split in
$\operatorname {\mathrm {Mod}}_{G/Z_G}^{\rm l.adm}(R)$. It must split in ![]() $\operatorname {\mathrm {Mod}}_{G/Z_G}^{\rm l.adm}(\mathcal {O})$, so we may find
$\operatorname {\mathrm {Mod}}_{G/Z_G}^{\rm l.adm}(\mathcal {O})$, so we may find ![]() $v\in \mathcal {E}$ such that
$v\in \mathcal {E}$ such that ![]() $\langle \mathcal {O}[G].v\rangle \cong \mathbf {1}_G$. It suffices to show that
$\langle \mathcal {O}[G].v\rangle \cong \mathbf {1}_G$. It suffices to show that ![]() $R$ acts on
$R$ acts on ![]() $v$ via the quotient
$v$ via the quotient ![]() $R\twoheadrightarrow R/\mathfrak {m}_R\cong \mathbb {F}$. This is clear, since if
$R\twoheadrightarrow R/\mathfrak {m}_R\cong \mathbb {F}$. This is clear, since if ![]() $x\in \mathfrak {m}_{R}$, then
$x\in \mathfrak {m}_{R}$, then ![]() $x\cdot v\in M^{\vee }$ and, if it were nonzero, then it would generate a subrepresentation of
$x\cdot v\in M^{\vee }$ and, if it were nonzero, then it would generate a subrepresentation of ![]() $M^{\vee }$ isomorphic to
$M^{\vee }$ isomorphic to ![]() $\mathbf {1}_G$, which is not possible by the first assertion.
$\mathbf {1}_G$, which is not possible by the first assertion.
Proposition 4.18 For any compact ![]() $R$-module
$R$-module ![]() $\mathrm {m}$, the natural map
$\mathrm {m}$, the natural map ![]() $v\mapsto (m\mapsto (v\widehat {\otimes } m))$ (where
$v\mapsto (m\mapsto (v\widehat {\otimes } m))$ (where ![]() $v\in \mathrm {m}$ and
$v\in \mathrm {m}$ and ![]() $m\in M$) induces an isomorphism
$m\in M$) induces an isomorphism
Remark 4.19 Note that ![]() $M$ is not projective in
$M$ is not projective in ![]() $\frak {C}_{G/Z_G}(R)$ so that we cannot apply [Reference PaškūnasPaš13, Lemma 2.9].
$\frak {C}_{G/Z_G}(R)$ so that we cannot apply [Reference PaškūnasPaš13, Lemma 2.9].
Proof. The proof is similar to [Reference Hu and PaškūnasHP19, Proposition 3.12]. As in [Reference Hu and PaškūnasHP19, Proposition 3.12], we may assume that ![]() $\mathrm {m}$ is of finite length. In particular, the completed tensor product
$\mathrm {m}$ is of finite length. In particular, the completed tensor product ![]() $\mathrm {m}\widehat {\otimes }_{R}M$ coincides with the usual one.
$\mathrm {m}\widehat {\otimes }_{R}M$ coincides with the usual one.
We proceed by induction on the length of ![]() $\mathrm {m}$. Note that since
$\mathrm {m}$. Note that since ![]() $R$ is a local ring, any
$R$ is a local ring, any ![]() $R$-module of length
$R$-module of length ![]() $1$ is isomorphic to
$1$ is isomorphic to ![]() $R/\mathfrak {m}_R\cong \mathbb {F}$. If
$R/\mathfrak {m}_R\cong \mathbb {F}$. If ![]() $\mathrm {m}\cong \mathbb {F}$, we need to show that
$\mathrm {m}\cong \mathbb {F}$, we need to show that ![]() $\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,\mathbb {F}\otimes _{R}M)\cong \mathbb {F}$. But any morphism
$\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,\mathbb {F}\otimes _{R}M)\cong \mathbb {F}$. But any morphism ![]() $M\rightarrow \mathbb {F}\otimes _{R}M$ in
$M\rightarrow \mathbb {F}\otimes _{R}M$ in ![]() $\frak {C}_{G/Z_G}(R)$ factors through
$\frak {C}_{G/Z_G}(R)$ factors through
so the assertion is reduced to
which is a direct consequence of Proposition 4.4. If the length of ![]() $\mathrm {m}$ is
$\mathrm {m}$ is ![]() $\geq 2$, let
$\geq 2$, let ![]() $\mathrm {m}_1\subset \mathrm {m}$ be a proper
$\mathrm {m}_1\subset \mathrm {m}$ be a proper ![]() $R$-submodule such that
$R$-submodule such that ![]() $\mathrm {m}_2:=\mathrm {m}/\mathrm {m}_1$ has length
$\mathrm {m}_2:=\mathrm {m}/\mathrm {m}_1$ has length ![]() $1$, i.e.
$1$, i.e. ![]() $\mathrm {m}_2\cong \mathbb {F}$. We then obtain a long exact sequence
$\mathrm {m}_2\cong \mathbb {F}$. We then obtain a long exact sequence
Since ![]() $\mathrm {m}_2\cong \mathbb {F}$ and
$\mathrm {m}_2\cong \mathbb {F}$ and ![]() $R$ is flat over
$R$ is flat over ![]() $R_{\overline {\rho }}^{\eta }$ by construction, we have
$R_{\overline {\rho }}^{\eta }$ by construction, we have
where the last isomorphism follows from [Reference HuHu21, Proposition 3.30]. By applying ![]() $\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,-)$ to (4.7) and using Lemma 4.17, we obtain the following short exact sequence
$\operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,-)$ to (4.7) and using Lemma 4.17, we obtain the following short exact sequence
By inductive hypothesis, we have ![]() $\mathrm {m}_i\xrightarrow {\sim } \operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,\mathrm {m}_i\otimes _{R}M)$ for
$\mathrm {m}_i\xrightarrow {\sim } \operatorname {{\mathrm {Hom}}}_{\frak {C}_{G/Z_G}(R)}(M,\mathrm {m}_i\otimes _{R}M)$ for ![]() $i\in \{1,2\}$, hence the result using the snake lemma.
$i\in \{1,2\}$, hence the result using the snake lemma.
Corollary 4.20 We have ![]() $\operatorname {{\mathrm {End}}}_{\frak {C}_{G/Z_G}(R)}(M)\cong R$. In particular,
$\operatorname {{\mathrm {End}}}_{\frak {C}_{G/Z_G}(R)}(M)\cong R$. In particular, ![]() $R$ acts faithfully on
$R$ acts faithfully on ![]() $M$.
$M$.
Proposition 4.21 Let ![]() $x_1,\ldots,x_g\in R$ be an
$x_1,\ldots,x_g\in R$ be an ![]() $M$-regular sequence. Then
$M$-regular sequence. Then ![]() $(x_1,\ldots,x_g)$ is also
$(x_1,\ldots,x_g)$ is also ![]() $R$-regular and
$R$-regular and
for any ![]() $1\leq i\leq g$.
$1\leq i\leq g$.
Proof. The proof is analogous to [Reference HuHu21, Proposition 5.11].
Since ![]() $R$ acts faithfully on
$R$ acts faithfully on ![]() $M$ by Corollary 4.20 and
$M$ by Corollary 4.20 and ![]() $x_1$ is
$x_1$ is ![]() $M$-regular,
$M$-regular, ![]() $x_1$ is also
$x_1$ is also ![]() $R$-regular. By Proposition 4.18, we have
$R$-regular. By Proposition 4.18, we have
This, in turn, shows that ![]() $R/x_1R$ acts faithfully on
$R/x_1R$ acts faithfully on ![]() $M/x_1M$, hence
$M/x_1M$, hence ![]() $x_2$ is
$x_2$ is ![]() $R/x_1R$-regular because it is
$R/x_1R$-regular because it is ![]() $M/x_1M$-regular by assumption. We may thus continue the above argument to conclude.
$M/x_1M$-regular by assumption. We may thus continue the above argument to conclude.
Remark 4.22 Proposition 4.21 could be used to prove a big ‘![]() $R=\mathbb {T}$’ theorem, see the proof of Proposition 8.20 below. Such a result is proved in [Reference Gee and NewtonGN22, Theorem B(3)] when
$R=\mathbb {T}$’ theorem, see the proof of Proposition 8.20 below. Such a result is proved in [Reference Gee and NewtonGN22, Theorem B(3)] when ![]() $R_{\overline {\rho }}^{\eta }$ is formally smooth, by first proving that a suitable patched module
$R_{\overline {\rho }}^{\eta }$ is formally smooth, by first proving that a suitable patched module ![]() $M_{\infty }$ is faithfully flat over the patched ring
$M_{\infty }$ is faithfully flat over the patched ring ![]() $R_{\infty }$ and then passing to the quotient. However, when
$R_{\infty }$ and then passing to the quotient. However, when ![]() $\overline {\rho } \sim \big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big ) \otimes \chi$,
$\overline {\rho } \sim \big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big ) \otimes \chi$, ![]() $R_{\overline {\rho }}^{\eta }$ is not formally smooth and the patched module
$R_{\overline {\rho }}^{\eta }$ is not formally smooth and the patched module ![]() $M_{\infty }$ is not flat over
$M_{\infty }$ is not flat over ![]() $R_{\infty }$, so the argument in [Reference Gee and NewtonGN22] does not apply. In addition, this case is also excluded in [Reference EmertonEme11, Theorem 1.3], so Proposition 4.21 may be of independent interest.
$R_{\infty }$, so the argument in [Reference Gee and NewtonGN22] does not apply. In addition, this case is also excluded in [Reference EmertonEme11, Theorem 1.3], so Proposition 4.21 may be of independent interest.
5. Automorphic forms and big patched modules
Let ![]() $F$ be a totally real extension of
$F$ be a totally real extension of ![]() $\mathbb {Q}$ in which
$\mathbb {Q}$ in which ![]() $p$ is unramified, and let
$p$ is unramified, and let ![]() ${\mathcal {O}}_F$ be its ring of integers. Let
${\mathcal {O}}_F$ be its ring of integers. Let ![]() $\Sigma _p$ denote the set of places of
$\Sigma _p$ denote the set of places of ![]() $F$ dividing
$F$ dividing ![]() $p$ and let
$p$ and let ![]() $\Sigma _{\infty }$ denote the set of infinite places of
$\Sigma _{\infty }$ denote the set of infinite places of ![]() $F$. For any place
$F$. For any place ![]() $v$ of
$v$ of ![]() $F$, let
$F$, let ![]() $F_v$ denote the completion of
$F_v$ denote the completion of ![]() $F$ at
$F$ at ![]() $v$ with ring of integers
$v$ with ring of integers ![]() ${\mathcal {O}}_{F_v}$, uniformizer
${\mathcal {O}}_{F_v}$, uniformizer ![]() $\varpi _v$ and residue field
$\varpi _v$ and residue field ![]() $k_{F_v}$. Let
$k_{F_v}$. Let ![]() $q_v$ denote the cardinality of
$q_v$ denote the cardinality of ![]() $k_{F_v}$. Let
$k_{F_v}$. Let ![]() ${\mathbb {A}}_{F,f}$ denote the ring of finite adèles of
${\mathbb {A}}_{F,f}$ denote the ring of finite adèles of ![]() $F$. If
$F$. If ![]() $S$ is a finite set of finite places of
$S$ is a finite set of finite places of ![]() $F$, let
$F$, let ![]() ${\mathbb {A}}^S_{F,f}$ denote the ring of finite adèles outside
${\mathbb {A}}^S_{F,f}$ denote the ring of finite adèles outside ![]() $S$. Recall
$S$. Recall ![]() $G_F=\operatorname {{\mathrm {Gal}}}({\overline {F}}/F)$ and
$G_F=\operatorname {{\mathrm {Gal}}}({\overline {F}}/F)$ and ![]() $G_{F_v}=\operatorname {{\mathrm {Gal}}}({\overline {F}}_v/F_v)$. By fixing an embedding
$G_{F_v}=\operatorname {{\mathrm {Gal}}}({\overline {F}}_v/F_v)$. By fixing an embedding ![]() ${\overline {F}}\hookrightarrow {\overline {F}}_v$,
${\overline {F}}\hookrightarrow {\overline {F}}_v$, ![]() $G_{F_v}$ is identified with the decomposition group at
$G_{F_v}$ is identified with the decomposition group at ![]() $v$. We let
$v$. We let ![]() $\operatorname {{\mathrm {Frob}}}_v\in G_{F_v}$ denote a (lift of the) geometric Frobenius element, and let
$\operatorname {{\mathrm {Frob}}}_v\in G_{F_v}$ denote a (lift of the) geometric Frobenius element, and let ![]() $\operatorname {{\mathrm {Art}}}_{F_v}$ denote the local Artin map, normalized so that it sends
$\operatorname {{\mathrm {Art}}}_{F_v}$ denote the local Artin map, normalized so that it sends ![]() $\varpi _v$ to
$\varpi _v$ to ![]() $\operatorname {{\mathrm {Frob}}}_v$. The global Artin map is denoted by
$\operatorname {{\mathrm {Frob}}}_v$. The global Artin map is denoted by ![]() $\operatorname {{\mathrm {Art}}}_F$ which is compatible with the local Artin map. We denote by
$\operatorname {{\mathrm {Art}}}_F$ which is compatible with the local Artin map. We denote by ![]() $\mathrm {rec}_{v}$ the local Langlands correspondence normalized as in the introduction of [Reference Harris and TaylorHT01], so that if
$\mathrm {rec}_{v}$ the local Langlands correspondence normalized as in the introduction of [Reference Harris and TaylorHT01], so that if ![]() $\pi$ is a smooth irreducible
$\pi$ is a smooth irreducible ![]() $\overline {\mathbb {Q}}_p$-representation of
$\overline {\mathbb {Q}}_p$-representation of ![]() $\mathrm {GL}_2(F_{v})$, then
$\mathrm {GL}_2(F_{v})$, then ![]() $\mathrm {rec}_{v}(\pi )$ is a Weil–Deligne representation of the Weil group
$\mathrm {rec}_{v}(\pi )$ is a Weil–Deligne representation of the Weil group ![]() $W_{F_v}$ defined over
$W_{F_v}$ defined over ![]() $\overline {\mathbb {Q}}_p$. Recall that
$\overline {\mathbb {Q}}_p$. Recall that ![]() $\mathbb {F}$ is a sufficiently large finite extension of
$\mathbb {F}$ is a sufficiently large finite extension of ![]() $\mathbb {F}_p$,
$\mathbb {F}_p$, ![]() $\mathcal {O} = W(\mathbb {F})$ and
$\mathcal {O} = W(\mathbb {F})$ and ![]() $E = \mathcal {O}[1/p]$. We prepare the global setup we need in this section.
$E = \mathcal {O}[1/p]$. We prepare the global setup we need in this section.
5.1 Tame types and the inertial local Langlands correspondence
Let ![]() $I_{F_{v}}$ be the inertia subgroup of
$I_{F_{v}}$ be the inertia subgroup of ![]() $G_{F_{v}}$. An inertial type at
$G_{F_{v}}$. An inertial type at ![]() $v$ is a two-dimensional representation
$v$ is a two-dimensional representation ![]() $\tau : I_{F_{v}} \to \mathrm {GL}_2(\overline {\mathbb {Q}}_p)$ with open kernel which extends to a representation of
$\tau : I_{F_{v}} \to \mathrm {GL}_2(\overline {\mathbb {Q}}_p)$ with open kernel which extends to a representation of ![]() $G_{F_{v}}$. We say
$G_{F_{v}}$. We say ![]() $\tau$ is a discrete series inertial type if it is either scalar, or extends to an irreducible representation of
$\tau$ is a discrete series inertial type if it is either scalar, or extends to an irreducible representation of ![]() $G_{F_{v}}$. In the latter case, we call
$G_{F_{v}}$. In the latter case, we call ![]() $\tau$ supercuspidal. We say
$\tau$ supercuspidal. We say ![]() $\tau$ is tame if it is trivial on the wild inertia subgroup. Under Henniart's inertial local Langlands correspondence [Reference HenniartHen02] (cf. also [Reference KisinKis09]), there is a unique finite-dimensional irreducible representation
$\tau$ is tame if it is trivial on the wild inertia subgroup. Under Henniart's inertial local Langlands correspondence [Reference HenniartHen02] (cf. also [Reference KisinKis09]), there is a unique finite-dimensional irreducible representation ![]() $\sigma (\tau )$ (respectively,
$\sigma (\tau )$ (respectively, ![]() $\sigma ^{\rm cr}(\tau )$) of
$\sigma ^{\rm cr}(\tau )$) of ![]() $\mathrm {GL}_2(\mathcal {O}_{F_{v}})$ over
$\mathrm {GL}_2(\mathcal {O}_{F_{v}})$ over ![]() $\overline {\mathbb {Q}}_p$-vector spaces, called types, satisfying if
$\overline {\mathbb {Q}}_p$-vector spaces, called types, satisfying if ![]() $\pi$ is an infinite-dimensional smooth irreducible representation of
$\pi$ is an infinite-dimensional smooth irreducible representation of ![]() $\mathrm {GL}_2(F_{v})$, then
$\mathrm {GL}_2(F_{v})$, then ![]() $\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma (\tau ),\pi ) \neq 0$ (respectively,
$\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma (\tau ),\pi ) \neq 0$ (respectively, ![]() $\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma ^{\rm cr}(\tau ),\pi ) \neq 0$) if and only if
$\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma ^{\rm cr}(\tau ),\pi ) \neq 0$) if and only if ![]() $\mathrm {rec}_{v}(\pi )|_{I_{F_{v}}} \cong \tau$ (respectively,
$\mathrm {rec}_{v}(\pi )|_{I_{F_{v}}} \cong \tau$ (respectively, ![]() $\mathrm {rec}_{v}(\pi )|_{I_{F_{v}}} \cong \tau$ and the monodromy operator
$\mathrm {rec}_{v}(\pi )|_{I_{F_{v}}} \cong \tau$ and the monodromy operator ![]() $N$ on
$N$ on ![]() $\mathrm {rec}_{v}(\pi )$ is zero), in which case the space
$\mathrm {rec}_{v}(\pi )$ is zero), in which case the space ![]() $\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma (\tau ),\pi )$ (respectively,
$\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma (\tau ),\pi )$ (respectively, ![]() $\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma ^{\rm cr}(\tau ),\pi )$) is one-dimensional. We always have
$\operatorname {{\mathrm {Hom}}}_{\mathrm {GL}_2(\mathcal {O}_{F_{v}})}(\sigma ^{\rm cr}(\tau ),\pi )$) is one-dimensional. We always have ![]() $\sigma (\tau ) = \sigma ^{\rm cr}(\tau )$ except when
$\sigma (\tau ) = \sigma ^{\rm cr}(\tau )$ except when ![]() $\tau = \chi \oplus \chi$, in which case
$\tau = \chi \oplus \chi$, in which case ![]() $\sigma (\chi \oplus \chi ) = {\rm sp}\otimes \chi \circ \det$ (here
$\sigma (\chi \oplus \chi ) = {\rm sp}\otimes \chi \circ \det$ (here ![]() ${\rm sp}$ denotes the Steinberg representation of
${\rm sp}$ denotes the Steinberg representation of ![]() $\mathrm {GL}_2(k_{F_v})$ over
$\mathrm {GL}_2(k_{F_v})$ over ![]() $\overline {\mathbb {Q}}_p$) and
$\overline {\mathbb {Q}}_p$) and ![]() $\sigma ^{\rm cr}(\chi \oplus \chi ) = \chi \circ \det$. Let
$\sigma ^{\rm cr}(\chi \oplus \chi ) = \chi \circ \det$. Let ![]() $\psi : \mathbb {F}_{q_v^2}^{\times } \to \overline {\mathbb {Q}}_p^{\times }$ be a character such that
$\psi : \mathbb {F}_{q_v^2}^{\times } \to \overline {\mathbb {Q}}_p^{\times }$ be a character such that ![]() $\psi \neq \psi ^{q_v}$. Let
$\psi \neq \psi ^{q_v}$. Let ![]() $\Theta (\psi )$ be the irreducible cuspidal
$\Theta (\psi )$ be the irreducible cuspidal ![]() $\overline {\mathbb {Q}}_p$-representation of
$\overline {\mathbb {Q}}_p$-representation of ![]() $\mathrm {GL}_2(k_{F_v})$ associated to
$\mathrm {GL}_2(k_{F_v})$ associated to ![]() $\psi$ as in [Reference DiamondDia07]. A tame supercuspidal type is an irreducible
$\psi$ as in [Reference DiamondDia07]. A tame supercuspidal type is an irreducible ![]() $\overline {\mathbb {Q}}_p$-representation of
$\overline {\mathbb {Q}}_p$-representation of ![]() $\mathrm {GL}_2(\mathcal {O}_{F_{v}})$ that arises by inflation from
$\mathrm {GL}_2(\mathcal {O}_{F_{v}})$ that arises by inflation from ![]() $\Theta (\psi )$ for some
$\Theta (\psi )$ for some ![]() $\psi$ as above.
$\psi$ as above.
In [Reference Gee and GeraghtyGG15], Gee and Geraghty developed an analogous theory for ![]() $D^{\times }$, where
$D^{\times }$, where ![]() $D$ is the nonsplit central quaternion algebra over
$D$ is the nonsplit central quaternion algebra over ![]() $F_{v}$. Let
$F_{v}$. Let ![]() $\mathrm {JL}$ denote the Jacquet–Langlands correspondence giving a bijection from irreducible smooth representations of
$\mathrm {JL}$ denote the Jacquet–Langlands correspondence giving a bijection from irreducible smooth representations of ![]() $D^{\times }$ over
$D^{\times }$ over ![]() $\overline {\mathbb {Q}}_p$ to discrete series representations of
$\overline {\mathbb {Q}}_p$ to discrete series representations of ![]() $\mathrm {GL}_2(F_v)$ over
$\mathrm {GL}_2(F_v)$ over ![]() $\overline {\mathbb {Q}}_p$. Let
$\overline {\mathbb {Q}}_p$. Let ![]() $\tau$ be a discrete series inertial type. By the Jacquet–Langlands correspondence, there is an irreducible smooth representation
$\tau$ be a discrete series inertial type. By the Jacquet–Langlands correspondence, there is an irreducible smooth representation ![]() $\pi _{D,\tau }$ of
$\pi _{D,\tau }$ of ![]() $D^{\times }$ such that
$D^{\times }$ such that ![]() $\mathrm {rec}_{v}(\mathrm {JL}(\pi _{D,\tau }))|_{I_{F_{v}}} \cong \tau$. Since
$\mathrm {rec}_{v}(\mathrm {JL}(\pi _{D,\tau }))|_{I_{F_{v}}} \cong \tau$. Since ![]() $F_{v}^{\times }\mathcal {O}_D^{\times }$ has index two in
$F_{v}^{\times }\mathcal {O}_D^{\times }$ has index two in ![]() $D^{\times }$,
$D^{\times }$, ![]() $\pi _{D,\tau }|_{\mathcal {O}_D^{\times }}$ is either irreducible or a sum of two irreducible representations which are conjugate under the uniformizer
$\pi _{D,\tau }|_{\mathcal {O}_D^{\times }}$ is either irreducible or a sum of two irreducible representations which are conjugate under the uniformizer ![]() $\varpi _D$ of
$\varpi _D$ of ![]() $D$. Let
$D$. Let ![]() $\sigma _D(\tau )$ be one of the irreducible components of
$\sigma _D(\tau )$ be one of the irreducible components of ![]() $\pi _{D,\tau }|_{\mathcal {O}_D^{\times }}$. If
$\pi _{D,\tau }|_{\mathcal {O}_D^{\times }}$. If ![]() $\pi _D$ is a smooth irreducible
$\pi _D$ is a smooth irreducible ![]() $\overline {\mathbb {Q}}_p$-representation of
$\overline {\mathbb {Q}}_p$-representation of ![]() $D^{\times }$, then
$D^{\times }$, then ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\sigma _D(\tau ),\pi _D) \neq 0$ if and only if
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\sigma _D(\tau ),\pi _D) \neq 0$ if and only if ![]() $\mathrm {rec}_{v}(\mathrm {JL}(\pi _D))|_{I_{F_{v}}} \cong \tau$, in which case,
$\mathrm {rec}_{v}(\mathrm {JL}(\pi _D))|_{I_{F_{v}}} \cong \tau$, in which case, ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\sigma _D(\tau ),\pi _D)$ is one-dimensional. If
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\sigma _D(\tau ),\pi _D)$ is one-dimensional. If ![]() $\tau$ is a tame inertial type, then
$\tau$ is a tame inertial type, then ![]() $\sigma (\tau )$ and
$\sigma (\tau )$ and ![]() $\sigma _D(\tau )$ can be defined over
$\sigma _D(\tau )$ can be defined over ![]() $E$ once
$E$ once ![]() $E$ is taken sufficiently large (and unramified), see the proof of [Reference Emerton, Gee and SavittEGS15, Lemma 3.1.1]. Recall the following lemma.
$E$ is taken sufficiently large (and unramified), see the proof of [Reference Emerton, Gee and SavittEGS15, Lemma 3.1.1]. Recall the following lemma.
Lemma 5.1 Let ![]() $\psi : \mathbb {F}_{q_v^2}^{\times } \to E^{\times }$ with
$\psi : \mathbb {F}_{q_v^2}^{\times } \to E^{\times }$ with ![]() $\psi \neq \psi ^{q_v}$. Let
$\psi \neq \psi ^{q_v}$. Let ![]() $\tau : = \psi \oplus \psi ^{q_v}$ be the supercuspidal inertial type associated to
$\tau : = \psi \oplus \psi ^{q_v}$ be the supercuspidal inertial type associated to ![]() $\psi$, where we denote by
$\psi$, where we denote by ![]() $\psi$ the composition
$\psi$ the composition ![]() $I_{F_v} \twoheadrightarrow \mathbb {F}_{q_v^2}^{\times } {\buildrel {\psi } \over \longrightarrow} E^{\times }$. Then
$I_{F_v} \twoheadrightarrow \mathbb {F}_{q_v^2}^{\times } {\buildrel {\psi } \over \longrightarrow} E^{\times }$. Then ![]() $\sigma (\tau ) = \Theta (\psi )$ and
$\sigma (\tau ) = \Theta (\psi )$ and ![]() $\pi _{D,\tau }|_{\mathcal {O}_{D}^{\times }} = \psi \oplus \psi ^{q_v}$.
$\pi _{D,\tau }|_{\mathcal {O}_{D}^{\times }} = \psi \oplus \psi ^{q_v}$.
Proof. The assertion on ![]() $\sigma (\tau )$ follows from Henniart's construction in [Reference HenniartHen02]. The assertion on
$\sigma (\tau )$ follows from Henniart's construction in [Reference HenniartHen02]. The assertion on ![]() $\sigma _D(\tau )$ follows from the classical Jacquet–Langlands correspondence; see, for example, [Reference Bushnell and HenniartBH06, Chapter 13].
$\sigma _D(\tau )$ follows from the classical Jacquet–Langlands correspondence; see, for example, [Reference Bushnell and HenniartBH06, Chapter 13].
5.2 Automorphic forms, Galois representations and the big patched modules
We define the space of automorphic forms. Let ![]() $B$ be a quaternion algebra over
$B$ be a quaternion algebra over ![]() $F$. Fix a maximal order
$F$. Fix a maximal order ![]() $\mathcal {O}_B$ of
$\mathcal {O}_B$ of ![]() $B$. Let
$B$. Let ![]() $\Sigma _B$ be the set of primes
$\Sigma _B$ be the set of primes ![]() $v$ in
$v$ in ![]() $F$ at which
$F$ at which ![]() $B$ is ramified. Let
$B$ is ramified. Let ![]() $\infty _{F}$ be a fixed infinite place of
$\infty _{F}$ be a fixed infinite place of ![]() $F$. We say
$F$. We say ![]() $B$ is definite if it is ramified at all infinite places;
$B$ is definite if it is ramified at all infinite places; ![]() $B$ is indefinite if it splits at
$B$ is indefinite if it splits at ![]() $\infty _F$ and ramifies at all other infinite places. If
$\infty _F$ and ramifies at all other infinite places. If ![]() $v$ is a finite place of
$v$ is a finite place of ![]() $F$, let
$F$, let ![]() $\mathcal {O}_{B_{v}}^{\times }$ denote the maximal compact subgroup of
$\mathcal {O}_{B_{v}}^{\times }$ denote the maximal compact subgroup of ![]() $B_{v}^{\times } : = (B\otimes _F F_v)^{\times }$. For
$B_{v}^{\times } : = (B\otimes _F F_v)^{\times }$. For ![]() $v \notin \Sigma _B$, we fix an isomorphism
$v \notin \Sigma _B$, we fix an isomorphism ![]() $B_{v}^{\times } \cong \mathrm {GL}_2(F_v)$ so that
$B_{v}^{\times } \cong \mathrm {GL}_2(F_v)$ so that ![]() $\mathcal {O}_{B_{v}}^{\times }$ is identified with
$\mathcal {O}_{B_{v}}^{\times }$ is identified with ![]() $\mathrm {GL}_2(\mathcal {O}_{F_v})$. Let
$\mathrm {GL}_2(\mathcal {O}_{F_v})$. Let ![]() $\psi :F^\times \setminus {\mathbb {A}}_{F,f}^\times \to \mathcal {O}^\times$ be a continuous character. Via the global Artin map,
$\psi :F^\times \setminus {\mathbb {A}}_{F,f}^\times \to \mathcal {O}^\times$ be a continuous character. Via the global Artin map, ![]() $\psi$ induces a continuous character
$\psi$ induces a continuous character ![]() $G_{F}\to \mathcal {O}^{\times }$ which, by abuse of notation, is again denoted by
$G_{F}\to \mathcal {O}^{\times }$ which, by abuse of notation, is again denoted by ![]() $\psi$. Assume, moreover, that
$\psi$. Assume, moreover, that ![]() $(F, B) \neq (\mathbb {Q}, \mathrm {GL}_{2})$.
$(F, B) \neq (\mathbb {Q}, \mathrm {GL}_{2})$.
Let ![]() $U$ be a compact open subgroup of
$U$ be a compact open subgroup of ![]() $(B\otimes _{F} {\mathbb {A}}_{F,f})^\times$. We denote by
$(B\otimes _{F} {\mathbb {A}}_{F,f})^\times$. We denote by ![]() $Y^B_U$ the finite set
$Y^B_U$ the finite set ![]() $B^\times \setminus (B\otimes _{F} {\mathbb {A}}_{F,f})^\times /U$ if
$B^\times \setminus (B\otimes _{F} {\mathbb {A}}_{F,f})^\times /U$ if ![]() $B$ is definite. If
$B$ is definite. If ![]() $B$ is indefinite, let
$B$ is indefinite, let ![]() $Y^B_U$ denote the quotient of
$Y^B_U$ denote the quotient of ![]() $X^B_U$ by the action of the finite group
$X^B_U$ by the action of the finite group ![]() $\mathbb {A}_{F,f}^{\times } / (F^{\times } (\mathbb {A}_{F,f}^{\times } \cap U))$, where
$\mathbb {A}_{F,f}^{\times } / (F^{\times } (\mathbb {A}_{F,f}^{\times } \cap U))$, where ![]() $X_U^B$ is the associated Shimura curve as in [Reference Breuil and DiamondBD14], which is the same convention used in [Reference EmertonEme11, Reference ScholzeScho18] but is different from the convention used in [Reference Buzzard, Diamond and JarvisBDJ10].
$X_U^B$ is the associated Shimura curve as in [Reference Breuil and DiamondBD14], which is the same convention used in [Reference EmertonEme11, Reference ScholzeScho18] but is different from the convention used in [Reference Buzzard, Diamond and JarvisBDJ10].
From now on until the end of the paper, we assume that ![]() $\Sigma _B$ and
$\Sigma _B$ and ![]() $\Sigma _p$ intersect at a unique place
$\Sigma _p$ intersect at a unique place ![]() $v$ above
$v$ above ![]() $p$. Fix
$p$. Fix ![]() $U^p = \prod _{w \nmid p} U_w$ a compact open subgroup of
$U^p = \prod _{w \nmid p} U_w$ a compact open subgroup of ![]() $(B\otimes _{F} \mathbb {A}^{\Sigma _p}_{F,f})^{\times }$. For each place
$(B\otimes _{F} \mathbb {A}^{\Sigma _p}_{F,f})^{\times }$. For each place ![]() $w \in \Sigma _p \setminus \{v\}$, let
$w \in \Sigma _p \setminus \{v\}$, let ![]() $\sigma _w$ be a finite free
$\sigma _w$ be a finite free ![]() $\mathcal {O}$-module equipped with a continuous action of
$\mathcal {O}$-module equipped with a continuous action of ![]() $U_w$ such that
$U_w$ such that ![]() $F_w^{\times }\cap U_w$ acts by
$F_w^{\times }\cap U_w$ acts by ![]() $\psi ^{-1}|_{F_w^{\times }}$. Denote
$\psi ^{-1}|_{F_w^{\times }}$. Denote
Let ![]() $U^{v}= U^p U_p^{v} \subset (B \otimes _F \mathbb {A}^{\{v\}}_{F,f})^{\times }$. Then
$U^{v}= U^p U_p^{v} \subset (B \otimes _F \mathbb {A}^{\{v\}}_{F,f})^{\times }$. Then ![]() $\sigma _p^v$ is equipped with an action of
$\sigma _p^v$ is equipped with an action of ![]() $U^v$ via the projection
$U^v$ via the projection ![]() $U^v \twoheadrightarrow U^{v}_p$. We extend this action to
$U^v \twoheadrightarrow U^{v}_p$. We extend this action to ![]() $U^v \mathbb {A}_{F,f}^{\times }$ by letting
$U^v \mathbb {A}_{F,f}^{\times }$ by letting ![]() $\mathbb {A}_{F,f}^{\times }$ act by
$\mathbb {A}_{F,f}^{\times }$ act by ![]() $\psi ^{-1}$. Assume that
$\psi ^{-1}$. Assume that ![]() $U_v$ is a compact open subgroup of
$U_v$ is a compact open subgroup of ![]() $\mathrm {GL}_2(\mathcal {O}_{F_v})$ such that
$\mathrm {GL}_2(\mathcal {O}_{F_v})$ such that ![]() $\psi |_{U_{v}\cap \mathcal {O}_{F_v}^\times }=1$. Then
$\psi |_{U_{v}\cap \mathcal {O}_{F_v}^\times }=1$. Then ![]() $\sigma _p^v$ admits an action of
$\sigma _p^v$ admits an action of ![]() $U^v U_v\mathbb {A}_{F,f}^{\times }$ by letting
$U^v U_v\mathbb {A}_{F,f}^{\times }$ by letting ![]() $U_v$ act trivially.
$U_v$ act trivially.
If ![]() $B$ is definite, set
$B$ is definite, set
 \begin{align*}
\widetilde{H}^{0,B}_{\sigma_p^v , \psi} (U^{v}, \mathcal{O}) &:=
\{f: B^\times\setminus (B\otimes_F {\mathbb{A}}_{F,f})^\times \to \sigma_p^v \,|\, f\ \text{is}\ \textit{continuous}\ \text{and}\ f(g u) = u^{-1} f(g), \\
&\quad\ \ \forall g\in (B\otimes_F {\mathbb{A}}_{F,f})^\times, \forall u \in U^v U_v \mathbb{A}_{F,f}^{\times}\}. \end{align*}
\begin{align*}
\widetilde{H}^{0,B}_{\sigma_p^v , \psi} (U^{v}, \mathcal{O}) &:=
\{f: B^\times\setminus (B\otimes_F {\mathbb{A}}_{F,f})^\times \to \sigma_p^v \,|\, f\ \text{is}\ \textit{continuous}\ \text{and}\ f(g u) = u^{-1} f(g), \\
&\quad\ \ \forall g\in (B\otimes_F {\mathbb{A}}_{F,f})^\times, \forall u \in U^v U_v \mathbb{A}_{F,f}^{\times}\}. \end{align*}
If ![]() $B$ is indefinite, let
$B$ is indefinite, let ![]() $\mathcal {F}_{\sigma _p^v/\varpi ^s}$ be the local system over
$\mathcal {F}_{\sigma _p^v/\varpi ^s}$ be the local system over ![]() $Y_{U^{v}U_{v}}^{B}$ associated to
$Y_{U^{v}U_{v}}^{B}$ associated to ![]() $\sigma _p^v/\varpi ^s$ (see [Reference EmertonEme06]), and set
$\sigma _p^v/\varpi ^s$ (see [Reference EmertonEme06]), and set
Both ![]() $\widetilde {H}^{0,B}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O})$ and
$\widetilde {H}^{0,B}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O})$ and ![]() $\widetilde {H}^{1,B}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O})$ carry an action of
$\widetilde {H}^{1,B}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O})$ carry an action of ![]() $(B\otimes _{F} F_{v})^\times$.
$(B\otimes _{F} F_{v})^\times$.
Let ![]() $S$ be a set of places of
$S$ be a set of places of ![]() $F$ containing all places in
$F$ containing all places in ![]() $\Sigma _{\infty } \cup \Sigma _B\cup \Sigma _p$, all places where
$\Sigma _{\infty } \cup \Sigma _B\cup \Sigma _p$, all places where ![]() $\psi$ is ramified, and all places
$\psi$ is ramified, and all places ![]() $w$ such that
$w$ such that ![]() $U_w$ is not
$U_w$ is not ![]() $\mathcal {O}_{B_w}^{\times }$. Let
$\mathcal {O}_{B_w}^{\times }$. Let ![]() $\overline {r}: G_{F} \to \mathrm {GL}_2(\mathbb {F})$ be an absolutely irreducible totally odd representation. Assume
$\overline {r}: G_{F} \to \mathrm {GL}_2(\mathbb {F})$ be an absolutely irreducible totally odd representation. Assume ![]() $\overline {r}$ is unramified outside
$\overline {r}$ is unramified outside ![]() $S$. Assume
$S$. Assume ![]() $\overline {\psi } := \psi \pmod {\varpi }$ is equal to
$\overline {\psi } := \psi \pmod {\varpi }$ is equal to ![]() $\omega \det \overline {r}$. Denote
$\omega \det \overline {r}$. Denote ![]() $\overline {r}_w {\overset {\rm {def}}{=}}\, \overline {r}|_{G_{F_w}}$. We make the following assumptions on
$\overline {r}_w {\overset {\rm {def}}{=}}\, \overline {r}|_{G_{F_w}}$. We make the following assumptions on ![]() $\overline {r}$:
$\overline {r}$:
(a)
 $\overline {r}$ is modular in the sense of [Reference Breuil and DiamondBD14, § 3.1],
$\overline {r}$ is modular in the sense of [Reference Breuil and DiamondBD14, § 3.1],  $\overline {r}|_{G_{F(\sqrt [p]{1})}}$ is absolutely irreducible and, if
$\overline {r}|_{G_{F(\sqrt [p]{1})}}$ is absolutely irreducible and, if  $p = 5$, the image of
$p = 5$, the image of  $\overline {r}(G_{F(\sqrt [p]{1})})$ in
$\overline {r}(G_{F(\sqrt [p]{1})})$ in  ${\rm PGL}_2(\mathbb {F})$ is not isomorphic to
${\rm PGL}_2(\mathbb {F})$ is not isomorphic to  ${\rm PSL}_2(\mathbb {F}_5)$;
${\rm PSL}_2(\mathbb {F}_5)$;(b) for
 $w \in S \setminus \Sigma _p$ the framed deformation ring of
$w \in S \setminus \Sigma _p$ the framed deformation ring of  $\overline {r}_w$ is formally smooth over
$\overline {r}_w$ is formally smooth over  $\mathcal {O}$ (cf. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Remark 8.1.1]);
$\mathcal {O}$ (cf. [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Remark 8.1.1]);(c) if
 $w\nmid p$ and
$w\nmid p$ and  $w \in \Sigma _B$, then
$w \in \Sigma _B$, then  $\overline {r}_w$ is either irreducible or a twist of an extension of the trivial representation by
$\overline {r}_w$ is either irreducible or a twist of an extension of the trivial representation by  $\overline {\varepsilon }$;
$\overline {\varepsilon }$;(d) if
 $w|p$,
$w|p$,  $w\neq v$, then
$w\neq v$, then  $\overline {r}|_{I_{F_w}}$ is generic in the sense of [Reference Breuil and PaškūnasBP12, Definition 11.7] (which is different from the genericity used in § 4.2.1).
$\overline {r}|_{I_{F_w}}$ is generic in the sense of [Reference Breuil and PaškūnasBP12, Definition 11.7] (which is different from the genericity used in § 4.2.1).
Assumption (c) is often called the compatibility condition between ![]() $B$ and
$B$ and ![]() $\overline {r}$. By [Reference Breuil and DiamondBD14, Corollaire 3.2.3], the above assumptions guarantee the non-vanishing of
$\overline {r}$. By [Reference Breuil and DiamondBD14, Corollaire 3.2.3], the above assumptions guarantee the non-vanishing of ![]() $\pi ^B(\overline {r})$, where
$\pi ^B(\overline {r})$, where ![]() $\pi ^B(\overline {r})$ is defined in (5.4). For each
$\pi ^B(\overline {r})$ is defined in (5.4). For each ![]() $w \in \Sigma _p\setminus \{v\}$, we fix a tame inertial type
$w \in \Sigma _p\setminus \{v\}$, we fix a tame inertial type ![]() $\tau _w$ over
$\tau _w$ over ![]() $E$ such that
$E$ such that ![]() $\det (\tau _w)|_{I_{F_w}}=\psi |_{I_{F_w}}$ and
$\det (\tau _w)|_{I_{F_w}}=\psi |_{I_{F_w}}$ and ![]() $\operatorname {{\mathrm {JH}}}( \overline {\sigma (\tau _w)}^{\rm ss})$ contains exactly one Serre weight in
$\operatorname {{\mathrm {JH}}}( \overline {\sigma (\tau _w)}^{\rm ss})$ contains exactly one Serre weight in ![]() $W(\overline {r}_w(1))$ [Reference Emerton, Gee and SavittEGS15, Proposition 3.5.1]. This is possible by our assumption (d) and (the proof of) [Reference Emerton, Gee and SavittEGS15, Proposition 3.5.1]. Let
$W(\overline {r}_w(1))$ [Reference Emerton, Gee and SavittEGS15, Proposition 3.5.1]. This is possible by our assumption (d) and (the proof of) [Reference Emerton, Gee and SavittEGS15, Proposition 3.5.1]. Let ![]() $\sigma ^{\circ }(\tau _w)$ be an
$\sigma ^{\circ }(\tau _w)$ be an ![]() $\mathcal {O}_{B_w}^{\times }$-stable
$\mathcal {O}_{B_w}^{\times }$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $\sigma (\tau _w)$ and
$\sigma (\tau _w)$ and
For ![]() $w$ a finite place of
$w$ a finite place of ![]() $F$, let
$F$, let ![]() $R_w$ denote the universal framed deformation ring of
$R_w$ denote the universal framed deformation ring of ![]() $\overline {r}_w$ over
$\overline {r}_w$ over ![]() ${\mathcal {O}}$. Let
${\mathcal {O}}$. Let ![]() $R_{w}^{\psi \varepsilon ^{-1}}$ denote the quotient of
$R_{w}^{\psi \varepsilon ^{-1}}$ denote the quotient of ![]() $R_{w}$ corresponding to liftings with determinant
$R_{w}$ corresponding to liftings with determinant ![]() $(\psi |_{F^\times _w})\varepsilon ^{-1}$. If
$(\psi |_{F^\times _w})\varepsilon ^{-1}$. If ![]() $w \in S\setminus \Sigma _p$,
$w \in S\setminus \Sigma _p$, ![]() $R^{\psi \varepsilon ^{-1}}_w$ is a formal power series ring in
$R^{\psi \varepsilon ^{-1}}_w$ is a formal power series ring in ![]() $3$-variables over
$3$-variables over ![]() $\mathcal {O}$ by our assumption (b). If
$\mathcal {O}$ by our assumption (b). If ![]() $w\,|\,p,\ w\neq v$, let
$w\,|\,p,\ w\neq v$, let ![]() $R_{w}^{\psi \varepsilon ^{-1}}((-1,0)_{\kappa },\tau _w)$ denote the reduced
$R_{w}^{\psi \varepsilon ^{-1}}((-1,0)_{\kappa },\tau _w)$ denote the reduced ![]() $p$-torsion-free quotient of
$p$-torsion-free quotient of ![]() $R_{w}^{\psi \varepsilon ^{-1}}$ corresponding to potentially crystalline (framed) deformations of inertial type
$R_{w}^{\psi \varepsilon ^{-1}}$ corresponding to potentially crystalline (framed) deformations of inertial type ![]() $\tau _w$ and Hodge–Tate weights
$\tau _w$ and Hodge–Tate weights ![]() $(-1,0)$ for all embeddings
$(-1,0)$ for all embeddings ![]() $\kappa : F_w\hookrightarrow E$. By the choice of
$\kappa : F_w\hookrightarrow E$. By the choice of ![]() $\tau _w$,
$\tau _w$, ![]() $R_{w}^{\psi \varepsilon ^{-1}}((-1,0)_{\kappa },\tau _w)$ is a formal power series ring in
$R_{w}^{\psi \varepsilon ^{-1}}((-1,0)_{\kappa },\tau _w)$ is a formal power series ring in ![]() $(3+[F_w:\mathbb {Q}_p])$-variables over
$(3+[F_w:\mathbb {Q}_p])$-variables over ![]() $\mathcal {O}$ (see [Reference Emerton, Gee and SavittEGS15, Theorem 7.2.1]). Let
$\mathcal {O}$ (see [Reference Emerton, Gee and SavittEGS15, Theorem 7.2.1]). Let
and
Let ![]() $R^{\Box, \psi \varepsilon ^{-1}}_{\overline {r},S}$ (respectively,
$R^{\Box, \psi \varepsilon ^{-1}}_{\overline {r},S}$ (respectively, ![]() $R^{\psi \varepsilon ^{-1}}_{\overline {r},S}$) be the framed (respectively, universal) deformation ring of
$R^{\psi \varepsilon ^{-1}}_{\overline {r},S}$) be the framed (respectively, universal) deformation ring of ![]() $\overline {r}$ parametrizing liftings (respectively, deformations) of
$\overline {r}$ parametrizing liftings (respectively, deformations) of ![]() $\overline {r}$ which are unramified outside
$\overline {r}$ which are unramified outside ![]() $S$ with determinant
$S$ with determinant ![]() $\psi \varepsilon ^{-1}$ as in [Reference Gee and KisinGK14, § 5.4.1]. Let
$\psi \varepsilon ^{-1}$ as in [Reference Gee and KisinGK14, § 5.4.1]. Let ![]() $r^{\rm univ}$ denote the universal deformation of
$r^{\rm univ}$ denote the universal deformation of ![]() $\overline {r}$ over
$\overline {r}$ over ![]() $R^{\psi \varepsilon ^{-1}}_{\overline {r} , S}$. Define
$R^{\psi \varepsilon ^{-1}}_{\overline {r} , S}$. Define ![]() $R^{\Box,\psi \varepsilon ^{-1}, \operatorname {{\mathrm {loc}}}}_{\overline {r},S}:=R^{\Box, \psi \varepsilon ^{-1}}_{\overline {r},S}\widehat {\otimes }_{R_S}R^{ \operatorname {{\mathrm {loc}}}}$. Let
$R^{\Box,\psi \varepsilon ^{-1}, \operatorname {{\mathrm {loc}}}}_{\overline {r},S}:=R^{\Box, \psi \varepsilon ^{-1}}_{\overline {r},S}\widehat {\otimes }_{R_S}R^{ \operatorname {{\mathrm {loc}}}}$. Let ![]() $R^{\psi \varepsilon ^{-1},\operatorname {{\mathrm {loc}}}}_{\overline {r} , S }$ denote the image of
$R^{\psi \varepsilon ^{-1},\operatorname {{\mathrm {loc}}}}_{\overline {r} , S }$ denote the image of ![]() $R^{\psi \varepsilon ^{-1}}_{\overline {r},S}$ in
$R^{\psi \varepsilon ^{-1}}_{\overline {r},S}$ in ![]() $R^{\Box,\psi \varepsilon ^{-1},\operatorname {{\mathrm {loc}}}}_{\overline {r},S}$.
$R^{\Box,\psi \varepsilon ^{-1},\operatorname {{\mathrm {loc}}}}_{\overline {r},S}$.
By [Reference Darmon, Diamond and TaylorDDT97, Lemma 4.11], there is a finite place ![]() $w_1\notin S$ with the following properties:
$w_1\notin S$ with the following properties:
–
 $q_{w_1}\not \equiv 1 \pmod {p}$;
$q_{w_1}\not \equiv 1 \pmod {p}$;– the ratio of the eigenvalues of
 $\overline {r}(\operatorname {{\mathrm {Frob}}}_{w_1})$ is not equal to
$\overline {r}(\operatorname {{\mathrm {Frob}}}_{w_1})$ is not equal to  $q_{w_1}^{\pm 1}$;
$q_{w_1}^{\pm 1}$;– the residue characteristic of
 $w_1$ is sufficiently large such that for any nontrivial root of unity
$w_1$ is sufficiently large such that for any nontrivial root of unity  $\zeta$ in a quadratic extension of
$\zeta$ in a quadratic extension of  $F$,
$F$,  $w_1$ does not divide
$w_1$ does not divide  $\zeta +\zeta ^{-1}-2$.
$\zeta +\zeta ^{-1}-2$.
Let ![]() $U = \prod _w U_w \subset (B \otimes _F \mathbb {A}_{F,f})^{\times }$ be a compact open subgroup satisfying:
$U = \prod _w U_w \subset (B \otimes _F \mathbb {A}_{F,f})^{\times }$ be a compact open subgroup satisfying:
–
 $U_w = \mathcal {O}_{B_w}^{\times }$ for
$U_w = \mathcal {O}_{B_w}^{\times }$ for  $w \notin S \cup \{w_1\};$
$w \notin S \cup \{w_1\};$–
 $U_{w_1}$ is contained in the subgroup of
$U_{w_1}$ is contained in the subgroup of  $(\mathcal {O}_B)_{w_1}^{\times } = \mathrm {GL}_2(\mathcal {O}_{F_{w_1}})$ consisting of matrices that are upper-triangular and unipotent modulo
$(\mathcal {O}_B)_{w_1}^{\times } = \mathrm {GL}_2(\mathcal {O}_{F_{w_1}})$ consisting of matrices that are upper-triangular and unipotent modulo  $\varpi _{w_1};$
$\varpi _{w_1};$– for places over
 $p$,
$p$,  $U_w = 1 +\varpi _w M_2(\mathcal {O}_{F_w})$ if
$U_w = 1 +\varpi _w M_2(\mathcal {O}_{F_w})$ if  $w\,|\,p$,
$w\,|\,p$,  $w\neq v;$
$w\neq v;$  $U_v$ is the subgroup
$U_v$ is the subgroup  $U^1_{B_v}$ defined in (2.2).
$U^1_{B_v}$ defined in (2.2).
By the choice of ![]() $U_{w_1}$,
$U_{w_1}$, ![]() $U$ is sufficiently small in the sense of [Reference Clozel, Harris and TaylorCHT08, § 3.3].
$U$ is sufficiently small in the sense of [Reference Clozel, Harris and TaylorCHT08, § 3.3].
[Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+16] and [Reference ScholzeScho18] extend the Taylor–Wiles–Kisin method to construct the big patched modules. The detailed construction for Shimura curves in the minimal case is given in [Reference Dotto and LeDL21, § 6]. By the arguments of [Reference Dotto and LeDL21], replacing ![]() $K^v$ in [Reference Dotto and LeDL21] by
$K^v$ in [Reference Dotto and LeDL21] by ![]() $U^v$, the representation
$U^v$, the representation ![]() $V = \bigotimes _{w \in S, w\neq v} V_w$ of
$V = \bigotimes _{w \in S, w\neq v} V_w$ of ![]() $K^v$ in [Reference Dotto and LeDL21] by the representation
$K^v$ in [Reference Dotto and LeDL21] by the representation ![]() $\sigma ^v_p$ of
$\sigma ^v_p$ of ![]() $U^v$, forgetting the Hecke operators
$U^v$, forgetting the Hecke operators ![]() $T_w$ at places
$T_w$ at places ![]() $w\in S'$, and allowing
$w\in S'$, and allowing ![]() $B$ possibly ramifies at some places above
$B$ possibly ramifies at some places above ![]() $p$, the same patching arguments produce a ‘big’ patched module
$p$, the same patching arguments produce a ‘big’ patched module ![]() $M_{\infty }^B$ with the following data. (Let
$M_{\infty }^B$ with the following data. (Let ![]() $j:=4 \# S - 1$ and let
$j:=4 \# S - 1$ and let ![]() $g,q$ be positive integers such that
$g,q$ be positive integers such that ![]() $q = g+ [F:\mathbb {Q}] - \# S +1$.)
$q = g+ [F:\mathbb {Q}] - \# S +1$.)
• A formal power series ring in
 $q$-variables
$q$-variables  $\mathcal {O}[\![z_1,\ldots,z_q]\!]$ with a homomorphism
which extends to a homomorphism from
$\mathcal {O}[\![z_1,\ldots,z_q]\!]$ with a homomorphism
which extends to a homomorphism from \[ \mathcal{O}[\![z_1,\ldots,z_q]\!] \to R^{\psi\varepsilon^{-1},\operatorname{{\mathrm{loc}}}}_{\overline{ r}, S} \]
\[ \mathcal{O}[\![z_1,\ldots,z_q]\!] \to R^{\psi\varepsilon^{-1},\operatorname{{\mathrm{loc}}}}_{\overline{ r}, S} \]
 $S_{\infty }:= \mathcal {O}[\![z_1,\ldots,z_q,y_1,\ldots,y_j]\!]$ to
$S_{\infty }:= \mathcal {O}[\![z_1,\ldots,z_q,y_1,\ldots,y_j]\!]$ to  $R^{\Box, \psi \varepsilon ^{-1},\operatorname {{\mathrm {loc}}}}_{\overline { r}, S}$.
$R^{\Box, \psi \varepsilon ^{-1},\operatorname {{\mathrm {loc}}}}_{\overline { r}, S}$.• There is a surjective homomorphism
where \[ R_{\infty}^{ \psi\varepsilon^{-1}} \twoheadrightarrow R^{\Box, \psi\varepsilon^{-1},\operatorname{{\mathrm{loc}}}}_{\overline{r}, S}, \]
\[ R_{\infty}^{ \psi\varepsilon^{-1}} \twoheadrightarrow R^{\Box, \psi\varepsilon^{-1},\operatorname{{\mathrm{loc}}}}_{\overline{r}, S}, \]
 $R_{\infty }^{ \psi \varepsilon ^{-1}}:= R^{ \operatorname {{\mathrm {loc}}}}[\![x_1,\ldots,x_g]\!]$. Let
$R_{\infty }^{ \psi \varepsilon ^{-1}}:= R^{ \operatorname {{\mathrm {loc}}}}[\![x_1,\ldots,x_g]\!]$. Let  $\frak {m}_{\infty }$ be the maximal ideal of
$\frak {m}_{\infty }$ be the maximal ideal of  $R_{\infty }^{ \psi \varepsilon ^{-1}}$.
$R_{\infty }^{ \psi \varepsilon ^{-1}}$.• An
 ${\mathcal {O}}$-algebra homomorphism
${\mathcal {O}}$-algebra homomorphism  $S_{\infty }\to R_{\infty }^{ \psi \varepsilon ^{-1}}$ such that
where
$S_{\infty }\to R_{\infty }^{ \psi \varepsilon ^{-1}}$ such that
where \[ R_{\infty}^{ \psi\varepsilon^{-1}}/\frak{a}_{\infty}\cong R^{\psi\varepsilon^{-1},\operatorname{{\mathrm{loc}}}}_{\overline{r}, S }, \]
\[ R_{\infty}^{ \psi\varepsilon^{-1}}/\frak{a}_{\infty}\cong R^{\psi\varepsilon^{-1},\operatorname{{\mathrm{loc}}}}_{\overline{r}, S }, \]
 $\frak {a}_{\infty }$ denotes the ideal
$\frak {a}_{\infty }$ denotes the ideal  $(z_1,\ldots,z_{q},y_1,\ldots,y_j)$ of
$(z_1,\ldots,z_{q},y_1,\ldots,y_j)$ of  $S_{\infty }$.
$S_{\infty }$.• A finitely generated Cohen–Macaulay
 $S_{\infty }[\![ \mathcal {O}_{B_v}^{\times } ]\!]$-module
$S_{\infty }[\![ \mathcal {O}_{B_v}^{\times } ]\!]$-module  $M^{B}_{\infty }$ equipped with an action of
$M^{B}_{\infty }$ equipped with an action of  $R_{\infty }^{ \psi \varepsilon ^{-1}}$, so that the action of
$R_{\infty }^{ \psi \varepsilon ^{-1}}$, so that the action of  $S_{\infty }$ factors through
$S_{\infty }$ factors through  $R_{\infty }^{ \psi \varepsilon ^{-1}}$. The module
$R_{\infty }^{ \psi \varepsilon ^{-1}}$. The module  $M^B_{\infty }$ is also Cohen–Macaulay over
$M^B_{\infty }$ is also Cohen–Macaulay over  $R_{\infty }^{ \psi \varepsilon ^{-1}}[\![ \mathcal {O}_{B_v}^{\times } ]\!]$ by [Reference Gee and NewtonGN22, Corollary A29]. Moreover,
$R_{\infty }^{ \psi \varepsilon ^{-1}}[\![ \mathcal {O}_{B_v}^{\times } ]\!]$ by [Reference Gee and NewtonGN22, Corollary A29]. Moreover,  $M^{B}_{\infty }$ is projective in the category
$M^{B}_{\infty }$ is projective in the category  $\frak {C}_{\mathcal {O}_{B_v}^{\times },\psi }(S_{\infty })$. Note that projectivity in the case where
$\frak {C}_{\mathcal {O}_{B_v}^{\times },\psi }(S_{\infty })$. Note that projectivity in the case where  $B$ ramifies at
$B$ ramifies at  $v$ follows from the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+16, Proposition 2.10] using [Reference NewtonNew13, Proposition 5.6]. Let
$v$ follows from the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+16, Proposition 2.10] using [Reference NewtonNew13, Proposition 5.6]. Let  $\frak {m}_{\overline {r}}$ be the maximal ideal of the abstract Hecke algebra associated to
$\frak {m}_{\overline {r}}$ be the maximal ideal of the abstract Hecke algebra associated to  $\overline {r}$ as in [Reference ScholzeScho18, § 5]. We have
(5.2)where
$\overline {r}$ as in [Reference ScholzeScho18, § 5]. We have
(5.2)where \begin{equation} M^{B}_{\infty} /
\frak{a}_{\infty} = \left\{{\begin{array}{@{}ll}
\widetilde{H}^{0,B}_{\sigma_p^v, \psi} (U^{v},
\mathcal{O})^d_{\frak{m}_{\overline{r}}} & \text{if}\ \text{B is
definite}, \\
\operatorname{{\mathrm{Hom}}}_{{\mathbb{T}}(U^v)_{\frak{m}_{\overline{r}}}[
G_{F}]} (r_{\frak{m}}, \widetilde{H}^{1,B}_{\sigma_p^v ,
\psi} (U^{v}, \mathcal{O})_{\frak{m}_{\overline{r}}})^d &
\text{if}\ B\ \text{is indefinite,} \end{array}}\right.
\end{equation}
\begin{equation} M^{B}_{\infty} /
\frak{a}_{\infty} = \left\{{\begin{array}{@{}ll}
\widetilde{H}^{0,B}_{\sigma_p^v, \psi} (U^{v},
\mathcal{O})^d_{\frak{m}_{\overline{r}}} & \text{if}\ \text{B is
definite}, \\
\operatorname{{\mathrm{Hom}}}_{{\mathbb{T}}(U^v)_{\frak{m}_{\overline{r}}}[
G_{F}]} (r_{\frak{m}}, \widetilde{H}^{1,B}_{\sigma_p^v ,
\psi} (U^{v}, \mathcal{O})_{\frak{m}_{\overline{r}}})^d &
\text{if}\ B\ \text{is indefinite,} \end{array}}\right.
\end{equation} ${\mathbb {T}}(U^v)_{\frak {m}_{\overline {r}}}$ denotes the Hecke algebra defined in the paragraph before [Reference ScholzeScho18, Proposition 5.7] (by taking
${\mathbb {T}}(U^v)_{\frak {m}_{\overline {r}}}$ denotes the Hecke algebra defined in the paragraph before [Reference ScholzeScho18, Proposition 5.7] (by taking  $\frak {p} = v$ and
$\frak {p} = v$ and  $\frak {m} = \frak {m}_{\overline {r}}$ in [Reference ScholzeScho18]), and
$\frak {m} = \frak {m}_{\overline {r}}$ in [Reference ScholzeScho18]), and  $r_{\frak {m}}$ denotes the composite
$r_{\frak {m}}$ denotes the composite
 \[ G_F {\buildrel {r^{\rm univ}} \over \longrightarrow} \mathrm{GL}_2(R^{\psi\varepsilon^{-1}}_{\overline{r},S}) \to \mathrm{GL}_2({\mathbb{T}}(U^v)_{\frak{m}_{\overline{r}}}). \]
\[ G_F {\buildrel {r^{\rm univ}} \over \longrightarrow} \mathrm{GL}_2(R^{\psi\varepsilon^{-1}}_{\overline{r},S}) \to \mathrm{GL}_2({\mathbb{T}}(U^v)_{\frak{m}_{\overline{r}}}). \]
Remark 5.2 In the indefinite case, there is a variant of ![]() $M_{\infty }^B$ denoted by
$M_{\infty }^B$ denoted by ![]() $N_{\infty }^B$, which is obtained by patching
$N_{\infty }^B$, which is obtained by patching ![]() $\widetilde {H}^{1,B}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O}/\varpi ^s)_{\frak {m}_{\overline {r}}}$ but without factorizing out
$\widetilde {H}^{1,B}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O}/\varpi ^s)_{\frak {m}_{\overline {r}}}$ but without factorizing out ![]() $r^{\rm univ}$. Namely, we have
$r^{\rm univ}$. Namely, we have
Let ![]() ${\rm Mod}_{\mathcal {O}^{\times }_{B_v},\psi }^{\rm fin}$ denote the category of finite
${\rm Mod}_{\mathcal {O}^{\times }_{B_v},\psi }^{\rm fin}$ denote the category of finite ![]() $\mathcal {O}$-modules with a continuous action of
$\mathcal {O}$-modules with a continuous action of ![]() $\mathcal {O}_{B_v}^{\times }$ such that the
$\mathcal {O}_{B_v}^{\times }$ such that the ![]() $\mathcal {O}_{B_v}^{\times }$-action has central character
$\mathcal {O}_{B_v}^{\times }$-action has central character ![]() $\psi |_{F_v^{\times }}$. Define a functor
$\psi |_{F_v^{\times }}$. Define a functor ![]() $M_{\infty }^B(-)$ from
$M_{\infty }^B(-)$ from ![]() ${\rm Mod}_{\mathcal {O}^{\times }_{B_v},\psi }^{\rm fin}$ to the category of finitely generated
${\rm Mod}_{\mathcal {O}^{\times }_{B_v},\psi }^{\rm fin}$ to the category of finitely generated ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$-modules by letting
$R_{\infty }^{\psi \varepsilon ^{-1}}$-modules by letting
By the projectivity of ![]() $M^{B}_{\infty }$ in
$M^{B}_{\infty }$ in ![]() $\frak {C}_{\mathcal {O}_{B_v}^{\times },\psi }(\mathcal {O})$,
$\frak {C}_{\mathcal {O}_{B_v}^{\times },\psi }(\mathcal {O})$, ![]() $M^{B}_{\infty }(-)$ is an exact functor. Define
$M^{B}_{\infty }(-)$ is an exact functor. Define
By definition, we have
At the place ![]() $v$, let
$v$, let ![]() $\tau _v : I_{F_v}\to \mathrm {GL}_2(E)$ be an inertial type and
$\tau _v : I_{F_v}\to \mathrm {GL}_2(E)$ be an inertial type and ![]() $\mathbf {w} = (a_{\kappa } , b_{\kappa })_{\kappa : F_v \hookrightarrow E}$ be a Hodge type with
$\mathbf {w} = (a_{\kappa } , b_{\kappa })_{\kappa : F_v \hookrightarrow E}$ be a Hodge type with ![]() $a_{\kappa } < b_{\kappa }$ for all
$a_{\kappa } < b_{\kappa }$ for all ![]() $\kappa$. Assume
$\kappa$. Assume ![]() $\tau _v$ is a discrete series inertial type if
$\tau _v$ is a discrete series inertial type if ![]() $B$ ramifies at
$B$ ramifies at ![]() $v$. Let
$v$. Let ![]() $R^{\psi \varepsilon ^{-1}}_{v}(\mathbf {w}, \tau _v)$ (respectively,
$R^{\psi \varepsilon ^{-1}}_{v}(\mathbf {w}, \tau _v)$ (respectively, ![]() $R^{\psi \varepsilon ^{-1}, {\rm cr}}_{v}(\mathbf {w}, \tau _v)$) denote the reduced
$R^{\psi \varepsilon ^{-1}, {\rm cr}}_{v}(\mathbf {w}, \tau _v)$) denote the reduced ![]() $p$-torsion-free quotient of
$p$-torsion-free quotient of ![]() $R_v^{\psi \varepsilon ^{-1}}$ which parametrizes potentially semistable (respectively, potentially crystalline) liftings of
$R_v^{\psi \varepsilon ^{-1}}$ which parametrizes potentially semistable (respectively, potentially crystalline) liftings of ![]() $\overline {r}_v$ of Galois type
$\overline {r}_v$ of Galois type ![]() $\tau _v$ and Hodge–Tate weights
$\tau _v$ and Hodge–Tate weights ![]() $\mathbf {w}$. Following [Reference Gee and GeraghtyGG15] let
$\mathbf {w}$. Following [Reference Gee and GeraghtyGG15] let ![]() $R^{\psi \varepsilon ^{-1}, {\rm ds}}_{v}(\mathbf {w}, \tau _v)$ denote the maximal reduced
$R^{\psi \varepsilon ^{-1}, {\rm ds}}_{v}(\mathbf {w}, \tau _v)$ denote the maximal reduced ![]() $p$-torsion-free quotient of
$p$-torsion-free quotient of ![]() $R^{\psi \varepsilon ^{-1}}_{v}(\mathbf {w} ,\tau _v)$ which is supported on the irreducible components where the associated Weil–Deligne representation is generically of discrete series type. Let
$R^{\psi \varepsilon ^{-1}}_{v}(\mathbf {w} ,\tau _v)$ which is supported on the irreducible components where the associated Weil–Deligne representation is generically of discrete series type. Let ![]() $R_{\infty }^{ \psi \varepsilon ^{-1}}(\mathbf {w},\tau _{v}):= R_{v}^{\psi \varepsilon ^{-1} }(\mathbf {w},\tau _{v}) \widehat {\otimes }_{R_{v}^{\psi \varepsilon ^{-1}}} R_{\infty }^{ \psi \varepsilon ^{-1}}$,
$R_{\infty }^{ \psi \varepsilon ^{-1}}(\mathbf {w},\tau _{v}):= R_{v}^{\psi \varepsilon ^{-1} }(\mathbf {w},\tau _{v}) \widehat {\otimes }_{R_{v}^{\psi \varepsilon ^{-1}}} R_{\infty }^{ \psi \varepsilon ^{-1}}$, ![]() $R_{\infty }^{\psi \varepsilon ^{-1} ,{\rm cr}}(\mathbf {w}, \tau _{v}):= R_{v}^{\psi \varepsilon ^{-1}, {\rm cr}}(\mathbf {w} ,\tau _{v}) \widehat {\otimes }_{R_{v}^{\psi \varepsilon ^{-1}}} R_{\infty }^{ \psi \varepsilon ^{-1}}$ and
$R_{\infty }^{\psi \varepsilon ^{-1} ,{\rm cr}}(\mathbf {w}, \tau _{v}):= R_{v}^{\psi \varepsilon ^{-1}, {\rm cr}}(\mathbf {w} ,\tau _{v}) \widehat {\otimes }_{R_{v}^{\psi \varepsilon ^{-1}}} R_{\infty }^{ \psi \varepsilon ^{-1}}$ and ![]() $R_{\infty }^{ \psi \varepsilon ^{-1}, {\rm ds}}(\mathbf {w},\tau _{v}):= R_{v}^{\psi \varepsilon ^{-1}, {\rm ds}}(\mathbf {w}, \tau _{v}) \widehat {\otimes }_{R_{v}^{\psi \varepsilon ^{-1}}} R_{\infty }^{ \psi \varepsilon ^{-1}}$.
$R_{\infty }^{ \psi \varepsilon ^{-1}, {\rm ds}}(\mathbf {w},\tau _{v}):= R_{v}^{\psi \varepsilon ^{-1}, {\rm ds}}(\mathbf {w}, \tau _{v}) \widehat {\otimes }_{R_{v}^{\psi \varepsilon ^{-1}}} R_{\infty }^{ \psi \varepsilon ^{-1}}$.
(i) If
 $\tau _v$ is a supercuspidal inertial type, then
$\tau _v$ is a supercuspidal inertial type, then  $R^{\psi \varepsilon ^{-1},{\rm ds}}_{v}(\mathbf {w}, \tau _v) = R^{\psi \varepsilon ^{-1} }_{v} (\mathbf {w},\tau _v)= R^{\psi \varepsilon ^{-1} ,{\rm cr}}_{v}(\mathbf {w}, \tau _v )$.
$R^{\psi \varepsilon ^{-1},{\rm ds}}_{v}(\mathbf {w}, \tau _v) = R^{\psi \varepsilon ^{-1} }_{v} (\mathbf {w},\tau _v)= R^{\psi \varepsilon ^{-1} ,{\rm cr}}_{v}(\mathbf {w}, \tau _v )$.(ii) If
 $\tau _v$ is a scalar type, then
$\tau _v$ is a scalar type, then  $R^{\psi \varepsilon ^{-1},{\rm ds}}_{v} (\mathbf {w}, \tau _v)$ corresponds to the closure of potentially semistable but not potentially crystalline points in
$R^{\psi \varepsilon ^{-1},{\rm ds}}_{v} (\mathbf {w}, \tau _v)$ corresponds to the closure of potentially semistable but not potentially crystalline points in  $\operatorname {{\mathrm {Spec}}} R^{\psi \varepsilon ^{-1} }_{v}(\mathbf {w},\tau _v )$.
$\operatorname {{\mathrm {Spec}}} R^{\psi \varepsilon ^{-1} }_{v}(\mathbf {w},\tau _v )$.
Proof. See [Reference Gee and GeraghtyGG15, § 5].
We assume ![]() $B$ ramifies at
$B$ ramifies at ![]() $v$ and
$v$ and ![]() $F_v= \mathbb {Q}_p$ for the rest of this section. Let
$F_v= \mathbb {Q}_p$ for the rest of this section. Let ![]() $\tau _v$ be supercuspidal and
$\tau _v$ be supercuspidal and ![]() $\mathbf {w} = (a,b)$ be as above satisfying
$\mathbf {w} = (a,b)$ be as above satisfying
We have a natural action of ![]() $B_{v}^{\times }$ on
$B_{v}^{\times }$ on ![]() $\mathrm {Sym}^{b - a -1} E^2 \otimes {\det }^{a}$ as follows: we fix an embedding
$\mathrm {Sym}^{b - a -1} E^2 \otimes {\det }^{a}$ as follows: we fix an embedding ![]() $B_{v}^{\times } \hookrightarrow \mathrm {GL}_2(\mathbb {Q}_{p^2})$. Then
$B_{v}^{\times } \hookrightarrow \mathrm {GL}_2(\mathbb {Q}_{p^2})$. Then ![]() $B_v^{\times }$ acts by the composite
$B_v^{\times }$ acts by the composite ![]() $B_{v}^{\times } \hookrightarrow \mathrm {GL}_2(\mathbb {Q}_{p^2}) \hookrightarrow \mathrm {GL}_2(E)$. Let
$B_{v}^{\times } \hookrightarrow \mathrm {GL}_2(\mathbb {Q}_{p^2}) \hookrightarrow \mathrm {GL}_2(E)$. Let ![]() $\Theta$ be any
$\Theta$ be any ![]() $\mathcal {O}_{B_{v}}^{\times }$-stable
$\mathcal {O}_{B_{v}}^{\times }$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in
The homomorphism ![]() $R_{\infty }^{\psi \varepsilon ^{-1}} \to \operatorname {{\mathrm {End}}}(M^B_{\infty }(\Theta ))$ factors through
$R_{\infty }^{\psi \varepsilon ^{-1}} \to \operatorname {{\mathrm {End}}}(M^B_{\infty }(\Theta ))$ factors through ![]() $R_{\infty }^{ \psi \varepsilon ^{-1}, {\rm ds}}(\mathbf {w},\tau _{v})$, which is
$R_{\infty }^{ \psi \varepsilon ^{-1}, {\rm ds}}(\mathbf {w},\tau _{v})$, which is ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ by Lemma 5.3(i), by the global Jacquet–Langlands correspondence and local–global compatibility. Since
$R_{\infty }^{\psi \varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ by Lemma 5.3(i), by the global Jacquet–Langlands correspondence and local–global compatibility. Since ![]() $S_{\infty }$ and
$S_{\infty }$ and ![]() $R_{\infty }^{ \psi \varepsilon ^{-1}}(\mathbf {w}, \tau _{v})$ have the same Krull dimension,
$R_{\infty }^{ \psi \varepsilon ^{-1}}(\mathbf {w}, \tau _{v})$ have the same Krull dimension, ![]() $M^B_{\infty }(\Theta )$ is maximal Cohen–Macaulay over
$M^B_{\infty }(\Theta )$ is maximal Cohen–Macaulay over ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ by the same argument of the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+16, Lemma 4.18].
$R_{\infty }^{\psi \varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ by the same argument of the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+16, Lemma 4.18].
Let ![]() $\delta :F^\times \setminus {\mathbb {A}}_{F,f}^\times \to \mathcal {O}^\times$ be a continuous character trivial on
$\delta :F^\times \setminus {\mathbb {A}}_{F,f}^\times \to \mathcal {O}^\times$ be a continuous character trivial on ![]() $U^{v}\cap {\mathbb {A}}_{F,f}^\times$ and trivial mod
$U^{v}\cap {\mathbb {A}}_{F,f}^\times$ and trivial mod ![]() $\varpi$. Sending a lifting
$\varpi$. Sending a lifting ![]() $r_w$ of
$r_w$ of ![]() $\overline {r}_w$ with determinant
$\overline {r}_w$ with determinant ![]() $\varepsilon ^{-1}\psi |_{F^\times _w}$ to
$\varepsilon ^{-1}\psi |_{F^\times _w}$ to ![]() $r_w\otimes \delta |_{F^{\times }_w}$ gives an isomorphism
$r_w\otimes \delta |_{F^{\times }_w}$ gives an isomorphism ![]() $\mathrm {tw}_{\delta |_{F_w^{\times }}}: R^{\psi \delta ^2\varepsilon ^{-1}}_w \xrightarrow {\sim } R_w^{\psi \varepsilon ^{-1}}$. We hence have an isomorphism
$\mathrm {tw}_{\delta |_{F_w^{\times }}}: R^{\psi \delta ^2\varepsilon ^{-1}}_w \xrightarrow {\sim } R_w^{\psi \varepsilon ^{-1}}$. We hence have an isomorphism ![]() $\mathrm {tw}_{\delta }:= \otimes _w \mathrm {tw}_{\delta |_{F_w^{\times }}}: R_{\infty }^{\psi \delta ^2 \varepsilon ^{-1}} \xrightarrow {\sim } R_{\infty }^{\psi \varepsilon ^{-1}}$. We have the following analogue of Corollary 4.6.
$\mathrm {tw}_{\delta }:= \otimes _w \mathrm {tw}_{\delta |_{F_w^{\times }}}: R_{\infty }^{\psi \delta ^2 \varepsilon ^{-1}} \xrightarrow {\sim } R_{\infty }^{\psi \varepsilon ^{-1}}$. We have the following analogue of Corollary 4.6.
Lemma 5.4 Let ![]() $(\mathbf {w},\tau _v)$ be as above satisfying
$(\mathbf {w},\tau _v)$ be as above satisfying ![]() $\varepsilon ^{b+a-1}|_{I_{F_v}}\det (\tau _v) |_{I_{F_v}} \sim (\psi \delta ^2)|_{I_{F_v}}$. Let
$\varepsilon ^{b+a-1}|_{I_{F_v}}\det (\tau _v) |_{I_{F_v}} \sim (\psi \delta ^2)|_{I_{F_v}}$. Let ![]() $\Theta$ be any
$\Theta$ be any ![]() $\mathcal {O}_{B_{v}}^{\times }$-stable
$\mathcal {O}_{B_{v}}^{\times }$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $\sigma _{B_v}(\mathbf {w},\tau _v) \otimes (\delta |_{F_v^{\times }}\circ {\rm Nrd})^{-1}$. Then
$\sigma _{B_v}(\mathbf {w},\tau _v) \otimes (\delta |_{F_v^{\times }}\circ {\rm Nrd})^{-1}$. Then ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}/\operatorname {{\mathrm {Ann}}}_{R_{\infty }^{\psi \varepsilon ^{-1}}}(M^B_{\infty }(\Theta ))$ is equal to
$R_{\infty }^{\psi \varepsilon ^{-1}}/\operatorname {{\mathrm {Ann}}}_{R_{\infty }^{\psi \varepsilon ^{-1}}}(M^B_{\infty }(\Theta ))$ is equal to ![]() $\mathrm {tw}_{\delta } (R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$ if
$\mathrm {tw}_{\delta } (R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$ if ![]() $R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ is an integral domain.
$R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ is an integral domain.
Proof. Note that ![]() $M_{\infty }^{B,\delta ^{-1}}: = M_{\infty }^B \otimes \delta ^{-1} \circ {\rm Nrd}$ is a ‘big’ patched module, which is finitely generated and Cohen–Macaulay over
$M_{\infty }^{B,\delta ^{-1}}: = M_{\infty }^B \otimes \delta ^{-1} \circ {\rm Nrd}$ is a ‘big’ patched module, which is finitely generated and Cohen–Macaulay over ![]() $S_{\infty }[\![ \mathcal {O}_{B_v}^{\times } ]\!]$ equipped with a compatible action of
$S_{\infty }[\![ \mathcal {O}_{B_v}^{\times } ]\!]$ equipped with a compatible action of ![]() $R_{\infty }^{ \psi \delta ^2\varepsilon ^{-1}}$. This is because
$R_{\infty }^{ \psi \delta ^2\varepsilon ^{-1}}$. This is because ![]() $\delta$ is trivial mod
$\delta$ is trivial mod ![]() $\varpi$, and when
$\varpi$, and when ![]() $B$ is definite, the map
$B$ is definite, the map ![]() $f\mapsto [g\mapsto f(g)(\delta \circ {\rm Nrd})^{-1}(g)]$ induces an isomorphism
$f\mapsto [g\mapsto f(g)(\delta \circ {\rm Nrd})^{-1}(g)]$ induces an isomorphism
which is compatible with the action of the Hecke algebra. Here ![]() $U(N)^v$ denotes the group
$U(N)^v$ denotes the group ![]() $U(N)^{\frak {p}}$ in the proof of [Reference Dospinescu, Paškūnas and SchraenDPS23, Theorem 8.10]. The isomorphism similar to (5.7) in the indefinite case follows from the proof of [Reference Buzzard, Diamond and JarvisBDJ10, Lemma 2.3]. Since
$U(N)^{\frak {p}}$ in the proof of [Reference Dospinescu, Paškūnas and SchraenDPS23, Theorem 8.10]. The isomorphism similar to (5.7) in the indefinite case follows from the proof of [Reference Buzzard, Diamond and JarvisBDJ10, Lemma 2.3]. Since ![]() $\Theta \otimes \delta |_{F_v^{\times }}\circ {\rm Nrd}$ is an
$\Theta \otimes \delta |_{F_v^{\times }}\circ {\rm Nrd}$ is an ![]() $\mathcal {O}_{B_v}^{\times }$-stable lattice in the locally algebraic representation
$\mathcal {O}_{B_v}^{\times }$-stable lattice in the locally algebraic representation ![]() $\sigma _{B_v}(\mathbf {w},\tau _v)$, the action of
$\sigma _{B_v}(\mathbf {w},\tau _v)$, the action of ![]() $R_{\infty }^{ \psi \delta ^2\varepsilon ^{-1}}$ on
$R_{\infty }^{ \psi \delta ^2\varepsilon ^{-1}}$ on ![]() $M_{\infty }^{B,\delta ^{-1}}(\Theta \otimes \delta |_{F_v^{\times }}\circ {\rm Nrd})$ factors through
$M_{\infty }^{B,\delta ^{-1}}(\Theta \otimes \delta |_{F_v^{\times }}\circ {\rm Nrd})$ factors through ![]() $R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$. Then the
$R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$. Then the ![]() $R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$-module
$R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$-module
is supported on a union of irreducible components of ![]() $\operatorname {{\mathrm {Spec}}}(R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$, which is all of
$\operatorname {{\mathrm {Spec}}}(R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$, which is all of ![]() $\operatorname {{\mathrm {Spec}}}(R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$ if
$\operatorname {{\mathrm {Spec}}}(R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$ if ![]() $R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ is an integral domain. The construction of the ‘big’ patched module and the relation with the associated Galois representation imply that the quotient ring
$R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} )$ is an integral domain. The construction of the ‘big’ patched module and the relation with the associated Galois representation imply that the quotient ring ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}/\operatorname {{\mathrm {Ann}}}_{R_{\infty }^{\psi \varepsilon ^{-1}}}(M^B_{\infty }(\Theta ))$ is equal to
$R_{\infty }^{\psi \varepsilon ^{-1}}/\operatorname {{\mathrm {Ann}}}_{R_{\infty }^{\psi \varepsilon ^{-1}}}(M^B_{\infty }(\Theta ))$ is equal to ![]() $\mathrm {tw}_{\delta } (R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$.
$\mathrm {tw}_{\delta } (R_{\infty }^{\psi \delta ^2\varepsilon ^{-1}}(\mathbf {w}, \tau _{v} ))$.
6. The Gelfand–Kirillov dimension of  $\pi ^B (\overline {r})$
$\pi ^B (\overline {r})$
In this section, we maintain the assumptions made in § 5. In particular, ![]() $B$ and
$B$ and ![]() $\overline {r}$ satisfy the compatibility condition (H0) of [Reference Breuil and DiamondBD14], which implies that
$\overline {r}$ satisfy the compatibility condition (H0) of [Reference Breuil and DiamondBD14], which implies that ![]() $\pi ^B(\overline {r})\neq 0$ by [Reference Breuil and DiamondBD14, Corollaire 3.2.3]. Since our main applications are for the quaternion algebra over
$\pi ^B(\overline {r})\neq 0$ by [Reference Breuil and DiamondBD14, Corollaire 3.2.3]. Since our main applications are for the quaternion algebra over ![]() $\mathbb {Q}_p$, we assume further that
$\mathbb {Q}_p$, we assume further that ![]() $F_v \cong \mathbb {Q}_p$, where
$F_v \cong \mathbb {Q}_p$, where ![]() $v$ is the unique place over
$v$ is the unique place over ![]() $p$ at which
$p$ at which ![]() $B$ is ramified. We denote by
$B$ is ramified. We denote by ![]() $D:= B_v$ the quaternion algebra over
$D:= B_v$ the quaternion algebra over ![]() $\mathbb {Q}_p$. We prove our main results on the Gelfand–Kirillov dimension of
$\mathbb {Q}_p$. We prove our main results on the Gelfand–Kirillov dimension of ![]() $\pi ^B (\overline {r})$ which is defined by (5.4). Assume
$\pi ^B (\overline {r})$ which is defined by (5.4). Assume ![]() $p\geq 5$.
$p\geq 5$.
6.1 Serre weights for quaternion algebras
Let ![]() $W_B(\overline {r})$ denote the set of modular quaternionic Serre weights at
$W_B(\overline {r})$ denote the set of modular quaternionic Serre weights at ![]() $v$ defined in [Reference Breuil and DiamondBD14, § 3.1]. Recall that an irreducible smooth representation of
$v$ defined in [Reference Breuil and DiamondBD14, § 3.1]. Recall that an irreducible smooth representation of ![]() $\mathcal {O}_{D}^{\times }$ over
$\mathcal {O}_{D}^{\times }$ over ![]() $\mathbb {F}$, equivalently a smooth character
$\mathbb {F}$, equivalently a smooth character ![]() $\chi :\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$, is in
$\chi :\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$, is in ![]() $W_B(\overline {r})$ if
$W_B(\overline {r})$ if
equivalently ![]() $M_{\infty }^B(\chi ) \neq 0$ by (5.5). Moreover,
$M_{\infty }^B(\chi ) \neq 0$ by (5.5). Moreover, ![]() $\dim _{\mathbb {F}} \operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }} (\chi, \pi ^B(\overline {r})) = \dim _{\mathbb {F}} M_{\infty }^B (\chi ) / \frak {m}_{\infty }$.
$\dim _{\mathbb {F}} \operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }} (\chi, \pi ^B(\overline {r})) = \dim _{\mathbb {F}} M_{\infty }^B (\chi ) / \frak {m}_{\infty }$.
Let ![]() $\overline {\rho }: = \overline {r}_v(1)$. Note that by our assumption
$\overline {\rho }: = \overline {r}_v(1)$. Note that by our assumption ![]() $\overline {\rho }$ is a two-dimensional continuous representation of
$\overline {\rho }$ is a two-dimensional continuous representation of ![]() $G_{\mathbb {Q}_p}$. We recall the definition of
$G_{\mathbb {Q}_p}$. We recall the definition of ![]() $W_{D}(\overline {\rho })$, the set of predicted quaternionic Serre weights for
$W_{D}(\overline {\rho })$, the set of predicted quaternionic Serre weights for ![]() $\overline {\rho }$, which is denoted by
$\overline {\rho }$, which is denoted by ![]() $W^?(\overline {\rho })$ in [Reference Gee and SavittGS11, Definition 3.4]. A character
$W^?(\overline {\rho })$ in [Reference Gee and SavittGS11, Definition 3.4]. A character ![]() $\psi : \mathcal {O}_D^{\times }\twoheadrightarrow \mathbb {F}_{p^2}^{\times }\to \mathbb {F}^{\times }$ is in
$\psi : \mathcal {O}_D^{\times }\twoheadrightarrow \mathbb {F}_{p^2}^{\times }\to \mathbb {F}^{\times }$ is in ![]() $W_D(\overline {\rho })$ if and only if
$W_D(\overline {\rho })$ if and only if ![]() $\overline {\rho }$ has a potentially Barsotti–Tate lift of type
$\overline {\rho }$ has a potentially Barsotti–Tate lift of type ![]() $[\psi ] \oplus [\psi ]^{p}$ if
$[\psi ] \oplus [\psi ]^{p}$ if ![]() $\psi \neq \psi ^p$, and
$\psi \neq \psi ^p$, and ![]() $\overline {\rho }$ has a potentially semistable lift of Hodge–Tate weights
$\overline {\rho }$ has a potentially semistable lift of Hodge–Tate weights ![]() $(0,1)$ and type
$(0,1)$ and type ![]() $[\psi ] \oplus [\psi ]$ which is not potentially crystalline if
$[\psi ] \oplus [\psi ]$ which is not potentially crystalline if ![]() $\psi = \psi ^p$.
$\psi = \psi ^p$.
We have the following description of the set ![]() $W_D(\overline {\rho })$.
$W_D(\overline {\rho })$.
Proposition 6.1 Recall ![]() $\xi :\mathbb {F}_{p^2}^{\times }\hookrightarrow \mathbb {F}^{\times }$ the character introduced in § 3.2. Let
$\xi :\mathbb {F}_{p^2}^{\times }\hookrightarrow \mathbb {F}^{\times }$ the character introduced in § 3.2. Let ![]() $\zeta$ denote the character
$\zeta$ denote the character ![]() $\xi ^{p+1}$, and let
$\xi ^{p+1}$, and let ![]() $\alpha$ denote the character
$\alpha$ denote the character ![]() $\xi ^{p-1}$.
$\xi ^{p-1}$.
(i) Assume
 $\overline {\rho }$ is in case 1 of § 4.1.1. We have the following.
$\overline {\rho }$ is in case 1 of § 4.1.1. We have the following.
(a) If
 $r \!\neq\! 0,p-1$ then
$r \!\neq\! 0,p-1$ then  $\chi \!\in\! W_D(\overline {\rho })$ if and only if
$\chi \!\in\! W_D(\overline {\rho })$ if and only if  $\chi \in \{ \xi ^r \zeta ^{s+1},\ \xi ^{pr} \zeta ^{s+1},\ \xi ^{r}\alpha ^{-1} \zeta ^{s+1},\ \xi ^{pr} \alpha \zeta ^{s+1}\}$.
$\chi \in \{ \xi ^r \zeta ^{s+1},\ \xi ^{pr} \zeta ^{s+1},\ \xi ^{r}\alpha ^{-1} \zeta ^{s+1},\ \xi ^{pr} \alpha \zeta ^{s+1}\}$.(b) If
 $r = 0$ or
$r = 0$ or  $p-1$, then
$p-1$, then  $\chi \in W_D(\overline {\rho })$ if and only if
$\chi \in W_D(\overline {\rho })$ if and only if  $\chi \in \{\alpha ^{-1} \zeta ^{s+1},\ \alpha \zeta ^{s+1}\}$.
$\chi \in \{\alpha ^{-1} \zeta ^{s+1},\ \alpha \zeta ^{s+1}\}$.
(ii) Assume
 $\overline {\rho }$ is in case 2 of § 4.1.1. We have the following.
$\overline {\rho }$ is in case 2 of § 4.1.1. We have the following.
(a) If
 $r=0$,
$r=0$,  ${\rm unr}_1 = {\rm unr}_2$ and
${\rm unr}_1 = {\rm unr}_2$ and  $\overline {\rho }$ is très ramifié, then
$\overline {\rho }$ is très ramifié, then  $\chi \in W_D(\overline {\rho })$ if and only if
$\chi \in W_D(\overline {\rho })$ if and only if  $\chi = \zeta ^{s+1}$.
$\chi = \zeta ^{s+1}$.(b) If
 $r=0$,
$r=0$,  ${\rm unr}_1 = {\rm unr}_2$ and
${\rm unr}_1 = {\rm unr}_2$ and  $\overline {\rho }$ is peu ramifié, then
$\overline {\rho }$ is peu ramifié, then  $\chi \in W_D(\overline {\rho })$ if and only if
$\chi \in W_D(\overline {\rho })$ if and only if  $\chi \in \{ \zeta ^{s+1},\ \alpha ^{-1} \zeta ^{s+1},\ \alpha \zeta ^{s+1} \}$.
$\chi \in \{ \zeta ^{s+1},\ \alpha ^{-1} \zeta ^{s+1},\ \alpha \zeta ^{s+1} \}$.(c) For other
 $\overline {\rho }$,
$\overline {\rho }$,  $\chi \in W_D(\overline {\rho })$ if and only if
$\chi \in W_D(\overline {\rho })$ if and only if  $\chi \in \{ \xi ^{r} \alpha ^{-1} \zeta ^{s+1},\ \xi ^{pr}\alpha \zeta ^{s+1} \}$.
$\chi \in \{ \xi ^{r} \alpha ^{-1} \zeta ^{s+1},\ \xi ^{pr}\alpha \zeta ^{s+1} \}$.
(iii) Assume
 $\overline {\rho }$ is in case 3 of § 4.1.1. We have the following.
$\overline {\rho }$ is in case 3 of § 4.1.1. We have the following.
(a) If
 $r= 0$ and
$r= 0$ and  ${\rm unr}_1 = {\rm unr}_2$, then
${\rm unr}_1 = {\rm unr}_2$, then  $\chi \in W_D(\overline {\rho })$ if and only if
$\chi \in W_D(\overline {\rho })$ if and only if  $\chi \in \{\zeta ^{s+1}, \alpha ^{-1} \zeta ^{s+1}, \alpha \zeta ^{s+1} \}$.
$\chi \in \{\zeta ^{s+1}, \alpha ^{-1} \zeta ^{s+1}, \alpha \zeta ^{s+1} \}$.(b) For other
 $\overline {\rho }$,
$\overline {\rho }$,  $\chi \in W_D(\overline {\rho })$ if and only if
$\chi \in W_D(\overline {\rho })$ if and only if  $\chi \in \{ \xi ^{r} \alpha ^{-1} \zeta ^{s+1},\ \xi ^{pr}\alpha \zeta ^{s+1}\}$.
$\chi \in \{ \xi ^{r} \alpha ^{-1} \zeta ^{s+1},\ \xi ^{pr}\alpha \zeta ^{s+1}\}$.
Proof. This follows from the definition of ![]() $W_D(\overline {\rho })$. More precisely, the Breuil–Mézard conjecture [Reference Breuil and MézardBM02], proved in [Reference KisinKis09, Reference PaškūnasPaš15, Reference Hu and TanHT15, Reference SanderSan16], states exactly when the involved deformation rings are nonzero in terms of
$W_D(\overline {\rho })$. More precisely, the Breuil–Mézard conjecture [Reference Breuil and MézardBM02], proved in [Reference KisinKis09, Reference PaškūnasPaš15, Reference Hu and TanHT15, Reference SanderSan16], states exactly when the involved deformation rings are nonzero in terms of ![]() $W(\overline {\rho })$ (cf. § 4.1.1). We take the case (ii)(b) as an example, so that
$W(\overline {\rho })$ (cf. § 4.1.1). We take the case (ii)(b) as an example, so that ![]() $W(\overline {\rho })=\{\sigma _{0,s+1},\sigma _{p-1,s+1}\}$. Up to twist we may assume
$W(\overline {\rho })=\{\sigma _{0,s+1},\sigma _{p-1,s+1}\}$. Up to twist we may assume ![]() $s=0$. It follows from the Breuil–Mézard conjecture and Proposition 3.6(ii) that
$s=0$. It follows from the Breuil–Mézard conjecture and Proposition 3.6(ii) that ![]() $\overline {\rho }$ has a potentially Barsotti–Tate lift of type
$\overline {\rho }$ has a potentially Barsotti–Tate lift of type ![]() $[\xi ^2]\oplus [\xi ^{2p}]$, so we obtain
$[\xi ^2]\oplus [\xi ^{2p}]$, so we obtain ![]() $\alpha ^{-1}\zeta,\alpha \zeta \in W_D(\overline {\rho })$. On the other hand,
$\alpha ^{-1}\zeta,\alpha \zeta \in W_D(\overline {\rho })$. On the other hand, ![]() $\overline {\rho }$ has a potentially semistable lift of Hodge–Tate weights
$\overline {\rho }$ has a potentially semistable lift of Hodge–Tate weights ![]() $(0,1)$ and type
$(0,1)$ and type ![]() $[\zeta ]\oplus [\zeta ]$ which is not potentially crystalline (see [Reference Breuil and MézardBM02, Théorème 1.2]), which gives
$[\zeta ]\oplus [\zeta ]$ which is not potentially crystalline (see [Reference Breuil and MézardBM02, Théorème 1.2]), which gives ![]() $\zeta \in W_D(\overline {\rho })$. Conversely, using the Breuil–Mézard conjecture again one checks that these exhaust all the Serre weights in
$\zeta \in W_D(\overline {\rho })$. Conversely, using the Breuil–Mézard conjecture again one checks that these exhaust all the Serre weights in ![]() $W_{D}(\overline {\rho })$.
$W_{D}(\overline {\rho })$.
Proposition 6.2 We have ![]() $W_B(\overline {r}) = W_D(\overline {\rho })$.
$W_B(\overline {r}) = W_D(\overline {\rho })$.
Proof. The inclusion ![]() $W_B(\overline {r}) \subseteq W_D(\overline {\rho })$ follows from [Reference Gee and SavittGS11, Lemma 3.3]. Note that [Reference Gee and SavittGS11] works only with definite
$W_B(\overline {r}) \subseteq W_D(\overline {\rho })$ follows from [Reference Gee and SavittGS11, Lemma 3.3]. Note that [Reference Gee and SavittGS11] works only with definite ![]() $B$ which ramifies at all places above
$B$ which ramifies at all places above ![]() $p$, but the argument also works in our case. By [Reference Gee and SavittGS11, Theorem 8.3], the two sets
$p$, but the argument also works in our case. By [Reference Gee and SavittGS11, Theorem 8.3], the two sets ![]() $W_B(\overline {r})$ and
$W_B(\overline {r})$ and ![]() $W_D(\overline {\rho })$ are identical in most cases with exception possibly when
$W_D(\overline {\rho })$ are identical in most cases with exception possibly when ![]() $\overline {\rho }$ is an unramified twist of
$\overline {\rho }$ is an unramified twist of ![]() $\big (\begin{smallmatrix} \omega & * \\ 0 & 1 \end{smallmatrix}\big ) \otimes \omega ^{s+1}$ and
$\big (\begin{smallmatrix} \omega & * \\ 0 & 1 \end{smallmatrix}\big ) \otimes \omega ^{s+1}$ and ![]() $\chi = \zeta ^{s+1} \in W_D(\overline {\rho })$. In this exceptional case,
$\chi = \zeta ^{s+1} \in W_D(\overline {\rho })$. In this exceptional case, ![]() $\overline {\rho }$ has a potentially semistable lift of type
$\overline {\rho }$ has a potentially semistable lift of type ![]() $[\chi ] \oplus [\chi ]$ which is not potentially crystalline. Applying [Reference Breuil and DiamondBD14, Théorème 3.2.2] (by taking
$[\chi ] \oplus [\chi ]$ which is not potentially crystalline. Applying [Reference Breuil and DiamondBD14, Théorème 3.2.2] (by taking ![]() $[r_v,N_v] = [[\chi ] \oplus [\chi ], N_v\neq 0]$ there), there is a Hilbert modular form over
$[r_v,N_v] = [[\chi ] \oplus [\chi ], N_v\neq 0]$ there), there is a Hilbert modular form over ![]() $F$ of parallel weight
$F$ of parallel weight ![]() $(2,\ldots,2)$ special at
$(2,\ldots,2)$ special at ![]() $v$ which gives
$v$ which gives ![]() $\overline {r}$. By global Jacquet–Langlands correspondence, as in the proof of [Reference Gee and SavittGS11, Lemma 3.3], we have
$\overline {r}$. By global Jacquet–Langlands correspondence, as in the proof of [Reference Gee and SavittGS11, Lemma 3.3], we have ![]() $\chi \in W_B(\overline {r})$.
$\chi \in W_B(\overline {r})$.
Remark 6.3 The question of determining the quaternionic Serre weights is first studied by Khare [Reference KhareKha01]. More precisely, [Reference KhareKha01, Theorem 7] proves that if ![]() $B_0$ denotes the definite quaternion algebra over
$B_0$ denotes the definite quaternion algebra over ![]() $\mathbb {Q}$ which is ramified exactly at
$\mathbb {Q}$ which is ramified exactly at ![]() $p$ and
$p$ and ![]() $\infty$, then
$\infty$, then ![]() $W_{B_0}(\overline {r}) = W_D(\overline {\rho })$.
$W_{B_0}(\overline {r}) = W_D(\overline {\rho })$.
6.2 Lattices in some locally algebraic representations of  $\mathcal {O}_D^{\times }$
$\mathcal {O}_D^{\times }$
Let ![]() $\chi$ be any character of
$\chi$ be any character of ![]() $\mathcal {O}_D^{\times }$ over
$\mathcal {O}_D^{\times }$ over ![]() $\mathbb {F}$. Recall that
$\mathbb {F}$. Recall that ![]() $W_{\chi,n}$ denotes
$W_{\chi,n}$ denotes ![]() $(\operatorname {{\mathrm {Proj}}}_{ \mathbb {F}[\![\mathcal {O}_D^{\times }/Z^1_D]\!]}\chi ) / \frak {m}_{D}^3$ for
$(\operatorname {{\mathrm {Proj}}}_{ \mathbb {F}[\![\mathcal {O}_D^{\times }/Z^1_D]\!]}\chi ) / \frak {m}_{D}^3$ for ![]() $n\geq 1$, where
$n\geq 1$, where ![]() $\frak {m}_{D}$ denotes the maximal ideal of the Iwasawa algebra
$\frak {m}_{D}$ denotes the maximal ideal of the Iwasawa algebra ![]() $\mathbb {F}[\![U^1_D / Z^1_D]\!]$. We construct suitable lattices
$\mathbb {F}[\![U^1_D / Z^1_D]\!]$. We construct suitable lattices ![]() $\mathcal {L}$ in locally algebraic representations of
$\mathcal {L}$ in locally algebraic representations of ![]() $\mathcal {O}_{D}^{\times }$ over
$\mathcal {O}_{D}^{\times }$ over ![]() $E$ so that
$E$ so that ![]() $\mathcal {L} / p\mathcal {L}$ is a quotient of
$\mathcal {L} / p\mathcal {L}$ is a quotient of ![]() $W_{\chi, 3} = (\operatorname {{\mathrm {Proj}}}_{\mathbb {F}[\![\mathcal {O}_D^{\times }/Z^1_D]\!]}\chi ) / \frak {m}_{D}^3$. The construction of these lattices is much easier than the case considered in § 3.
$W_{\chi, 3} = (\operatorname {{\mathrm {Proj}}}_{\mathbb {F}[\![\mathcal {O}_D^{\times }/Z^1_D]\!]}\chi ) / \frak {m}_{D}^3$. The construction of these lattices is much easier than the case considered in § 3.
Recall that ![]() $\mathcal {O}_D^{\times }$ embeds into
$\mathcal {O}_D^{\times }$ embeds into ![]() $\mathrm {GL}_2(\mathbb {Z}_{p^2})$ and then embeds into
$\mathrm {GL}_2(\mathbb {Z}_{p^2})$ and then embeds into ![]() $\mathrm {GL}_2(\mathcal {O})$ via the embedding
$\mathrm {GL}_2(\mathcal {O})$ via the embedding ![]() $\mathrm {GL}_2(\mathbb {Z}_{p^2}) \subset \mathrm {GL}_2(\mathcal {O})$. An explicit embedding is given by (cf. (2.1))
$\mathrm {GL}_2(\mathbb {Z}_{p^2}) \subset \mathrm {GL}_2(\mathcal {O})$. An explicit embedding is given by (cf. (2.1))
Let ![]() $\mathcal {O}_D^{\times }$ act on
$\mathcal {O}_D^{\times }$ act on ![]() $\mathrm {Sym}^1\mathcal {O}^2$ and
$\mathrm {Sym}^1\mathcal {O}^2$ and ![]() $\mathrm {Sym}^1 E^2$ via the above embedding. Precisely, for
$\mathrm {Sym}^1 E^2$ via the above embedding. Precisely, for ![]() $a,b\in \mathbb {Z}_{p^2}$,
$a,b\in \mathbb {Z}_{p^2}$,
Equipped with this action, ![]() $\mathrm {Sym}^1 \mathcal {O}^2$ and
$\mathrm {Sym}^1 \mathcal {O}^2$ and ![]() $\mathrm {Sym}^1 E^2$ are continuous representations of
$\mathrm {Sym}^1 E^2$ are continuous representations of ![]() $\mathcal {O}_D^{\times }$. Let
$\mathcal {O}_D^{\times }$. Let ![]() $\mathrm {pr}:\mathbb {Q}_p^{\times }\rightarrow 1+p\mathbb {Z}_p$ denote the projection sending
$\mathrm {pr}:\mathbb {Q}_p^{\times }\rightarrow 1+p\mathbb {Z}_p$ denote the projection sending ![]() $p$ to
$p$ to ![]() $1$. Let
$1$. Let ![]() $\underline {\mathrm {Sym}}^1 \mathcal {O}^2$ (respectively,
$\underline {\mathrm {Sym}}^1 \mathcal {O}^2$ (respectively, ![]() $\underline {\mathrm {Sym}}^1 E^2$) denote the continuous
$\underline {\mathrm {Sym}}^1 E^2$) denote the continuous ![]() $\mathcal {O}_D^{\times }$-module
$\mathcal {O}_D^{\times }$-module ![]() $\mathrm {Sym}^1\mathcal {O}^2\otimes (\mathrm {pr}\circ {\rm Nrd}_D)^{-1/2}$ (respectively,
$\mathrm {Sym}^1\mathcal {O}^2\otimes (\mathrm {pr}\circ {\rm Nrd}_D)^{-1/2}$ (respectively, ![]() $\mathrm {Sym}^1 E^2\otimes (\mathrm {pr}\circ {\rm Nrd}_D)^{-1/2}$), where
$\mathrm {Sym}^1 E^2\otimes (\mathrm {pr}\circ {\rm Nrd}_D)^{-1/2}$), where ![]() ${\rm Nrd}_D:D^{\times } \to \mathbb {Q}_p^{\times }$ is the reduced norm. One checks that
${\rm Nrd}_D:D^{\times } \to \mathbb {Q}_p^{\times }$ is the reduced norm. One checks that ![]() $Z_D^1$ acts trivially on
$Z_D^1$ acts trivially on ![]() $\underline {\mathrm {Sym}}^1 E^2$. Note that
$\underline {\mathrm {Sym}}^1 E^2$. Note that ![]() $(\underline {\mathrm {Sym}}^1 \mathcal {O}^2) /p \cong \mathrm {Sym}^1 \mathbb {F}^2$ with semisimplification
$(\underline {\mathrm {Sym}}^1 \mathcal {O}^2) /p \cong \mathrm {Sym}^1 \mathbb {F}^2$ with semisimplification ![]() $(\mathrm {Sym}^1 \mathbb {F}^2)^{\rm ss} = \chi _1 \oplus \chi _2$, where
$(\mathrm {Sym}^1 \mathbb {F}^2)^{\rm ss} = \chi _1 \oplus \chi _2$, where ![]() $\chi _1,\chi _2$ are characters of
$\chi _1,\chi _2$ are characters of ![]() $\mathcal {O}_D^{\times }$ determined by
$\mathcal {O}_D^{\times }$ determined by ![]() $\chi _1 (t) = t$,
$\chi _1 (t) = t$, ![]() $\chi _2 (t) = t^p$ for all
$\chi _2 (t) = t^p$ for all ![]() $t \in \mathbb {F}_{p^2}^{\times }$. In particular,
$t \in \mathbb {F}_{p^2}^{\times }$. In particular, ![]() $\chi _1=\chi _2\alpha ^{-1}$. By Proposition 2.13 we have
$\chi _1=\chi _2\alpha ^{-1}$. By Proposition 2.13 we have
so there exist (up to isomorphism) unique nonsplit extensions ![]() $(\chi _1\ \textbf {---}\ \chi _2)$ and
$(\chi _1\ \textbf {---}\ \chi _2)$ and ![]() $(\chi _2\ \textbf {---}\ \chi _1)$.
$(\chi _2\ \textbf {---}\ \chi _1)$.
Lemma 6.4 There exist ![]() $\mathcal {O}_D^{\times }$-stable
$\mathcal {O}_D^{\times }$-stable ![]() $\mathcal {O}$-lattices
$\mathcal {O}$-lattices ![]() $L,L'$ in
$L,L'$ in ![]() $\underline {\mathrm {Sym}}^1 E^2$ such that:
$\underline {\mathrm {Sym}}^1 E^2$ such that:
(a)
 $pL\subset L'\subset L$;
$pL\subset L'\subset L$;(b)
 $L/pL\cong (\chi _1\ \textbf {---}\ \chi _2)$ and
$L/pL\cong (\chi _1\ \textbf {---}\ \chi _2)$ and  $L'/pL'\cong (\chi _2\ \textbf {---}\ \chi _1)$.
$L'/pL'\cong (\chi _2\ \textbf {---}\ \chi _1)$.
Proof. We take ![]() $L=\underline {\mathrm {Sym}}^1\mathcal {O}^2=\mathcal {O}( Y \otimes 1)\oplus \mathcal {O} (X\otimes 1)$ and
$L=\underline {\mathrm {Sym}}^1\mathcal {O}^2=\mathcal {O}( Y \otimes 1)\oplus \mathcal {O} (X\otimes 1)$ and ![]() $L'=\mathcal {O} (X\otimes 1)\oplus p\mathcal {O} (Y\otimes 1)$. The properties are easily checked using (6.1).
$L'=\mathcal {O} (X\otimes 1)\oplus p\mathcal {O} (Y\otimes 1)$. The properties are easily checked using (6.1).
Let ![]() $\chi : \mathcal {O}_D^{\times } \to \mathbb {F}^{\times }$ be a character. Then there exist integers
$\chi : \mathcal {O}_D^{\times } \to \mathbb {F}^{\times }$ be a character. Then there exist integers ![]() $-2 \leq a \leq p-2$,
$-2 \leq a \leq p-2$, ![]() $b\in \mathbb {Z}$ such that
$b\in \mathbb {Z}$ such that
where ![]() $[-]$ denotes the Teichmüller lift. We write
$[-]$ denotes the Teichmüller lift. We write
Let ![]() $\Theta _1: = \psi _1$, viewed as an
$\Theta _1: = \psi _1$, viewed as an ![]() $\mathcal {O}_D^{\times }$-stable lattice in
$\mathcal {O}_D^{\times }$-stable lattice in ![]() $V_1 := \psi _1 \otimes _{\mathcal {O}} E$. For
$V_1 := \psi _1 \otimes _{\mathcal {O}} E$. For ![]() $i =2,3$, let
$i =2,3$, let
Note that ![]() $Z_D\cap \mathcal {O}_D^{\times }$ acts on
$Z_D\cap \mathcal {O}_D^{\times }$ acts on ![]() $V_i$ by the same character
$V_i$ by the same character ![]() $[\chi ]$. The
$[\chi ]$. The ![]() $\mathcal {O}_D^{\times }$-representations
$\mathcal {O}_D^{\times }$-representations ![]() $V_i,~1\leq i\leq 3$ are irreducible and
$V_i,~1\leq i\leq 3$ are irreducible and
An analogue of Proposition 3.7 implies that there exists a unique (up to homothety) ![]() $\mathcal {O}_D^{\times }$-stable
$\mathcal {O}_D^{\times }$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $V_i$, say
$V_i$, say ![]() $\Theta _i$, such that
$\Theta _i$, such that ![]() $\mathrm {cosoc}_{\mathcal {O}_D^{\times }}(\Theta _i / p \Theta _i) = \chi$ for
$\mathrm {cosoc}_{\mathcal {O}_D^{\times }}(\Theta _i / p \Theta _i) = \chi$ for ![]() $i =2,3$. We have surjective maps
$i =2,3$. We have surjective maps
Let ![]() $\Theta _i':=\operatorname {{\mathrm {Ker}}}(r_i)$ for
$\Theta _i':=\operatorname {{\mathrm {Ker}}}(r_i)$ for ![]() $i=2,3$. Then by Lemma 6.4 we have
$i=2,3$. Then by Lemma 6.4 we have
Since every irreducible representation of ![]() $\mathcal {O}_D^{\times }$ over
$\mathcal {O}_D^{\times }$ over ![]() $\mathbb {F}$ is one-dimensional,
$\mathbb {F}$ is one-dimensional, ![]() $\Theta _1 / p\Theta _1$ is killed by
$\Theta _1 / p\Theta _1$ is killed by ![]() $\frak {m}_{D}$, while
$\frak {m}_{D}$, while ![]() $\Theta _i / p\Theta _i$ and
$\Theta _i / p\Theta _i$ and ![]() $\Theta '_i / p\Theta '_i$ are killed by
$\Theta '_i / p\Theta '_i$ are killed by ![]() $\frak {m}^2_{D}$ for
$\frak {m}^2_{D}$ for ![]() $i=2,3$. By construction,
$i=2,3$. By construction, ![]() $\Theta _1$,
$\Theta _1$, ![]() $\Theta _2$ and
$\Theta _2$ and ![]() $\Theta _3$ are quotients of
$\Theta _3$ are quotients of ![]() $\operatorname {{\mathrm {Proj}}}_{ \mathcal {O}[\![\mathcal {O}_D^{\times }/Z^1_D]\!]}\chi$.
$\operatorname {{\mathrm {Proj}}}_{ \mathcal {O}[\![\mathcal {O}_D^{\times }/Z^1_D]\!]}\chi$.
We now glue the three lattices ![]() $\Theta _1$,
$\Theta _1$, ![]() $\Theta _2$ and
$\Theta _2$ and ![]() $\Theta _3$. We first glue
$\Theta _3$. We first glue ![]() $\Theta _1$ and
$\Theta _1$ and ![]() $\Theta _2$ along
$\Theta _2$ along ![]() $\chi$, namely define
$\chi$, namely define ![]() $\Theta$ by the short exact sequence
$\Theta$ by the short exact sequence
(i) There is a short exact sequence
 $0\rightarrow \Theta _2'/p\Theta _2'\rightarrow \Theta /p\Theta \rightarrow \chi \rightarrow 0$.
$0\rightarrow \Theta _2'/p\Theta _2'\rightarrow \Theta /p\Theta \rightarrow \chi \rightarrow 0$.(ii) The cosocle of
 $\Theta /p\Theta$ is isomorphic to
$\Theta /p\Theta$ is isomorphic to  $\chi$. Moreover, the cosocle filtration of
$\chi$. Moreover, the cosocle filtration of  $\Theta /p\Theta$ is
$\Theta /p\Theta$ is
 \[ \chi\ \textbf{---}\ \chi\alpha^{-1}\ \textbf{---}\ \chi. \]
\[ \chi\ \textbf{---}\ \chi\alpha^{-1}\ \textbf{---}\ \chi. \]
Proof. Clearly, Lemmas 3.3 and 3.4 remain true if we are considering ![]() $\mathcal {O}_D^{\times }$-representations instead of
$\mathcal {O}_D^{\times }$-representations instead of ![]() $\mathrm {GL}_2(\mathbb {Z}_p)$-representations. The results follow from them.
$\mathrm {GL}_2(\mathbb {Z}_p)$-representations. The results follow from them.
Let ![]() $r$ denote the map
$r$ denote the map ![]() $\Theta \twoheadrightarrow \Theta /p\Theta \twoheadrightarrow \chi$ where the second map is as in Proposition 6.5(i). Denote by
$\Theta \twoheadrightarrow \Theta /p\Theta \twoheadrightarrow \chi$ where the second map is as in Proposition 6.5(i). Denote by ![]() $\widetilde {\Theta }$ the lattice in
$\widetilde {\Theta }$ the lattice in ![]() $V_1 \oplus V_2 \oplus V_3$ obtained by gluing
$V_1 \oplus V_2 \oplus V_3$ obtained by gluing ![]() $\Theta$ and
$\Theta$ and ![]() $\Theta _3$ along
$\Theta _3$ along ![]() $\chi$. Namely,
$\chi$. Namely, ![]() $\widetilde {\Theta }$ is defined by the following short exact sequence
$\widetilde {\Theta }$ is defined by the following short exact sequence
(i) The cosocle of
 $\widetilde {\Theta }/p\widetilde {\Theta }$ is isomorphic to
$\widetilde {\Theta }/p\widetilde {\Theta }$ is isomorphic to  $\chi$.
$\chi$.(ii) We have that
 $\widetilde {\Theta }/p \widetilde {\Theta }$ is a quotient of
$\widetilde {\Theta }/p \widetilde {\Theta }$ is a quotient of  $W_{\chi,3}$. More precisely,
$W_{\chi,3}$. More precisely,  $\widetilde {\Theta }/p\widetilde {\Theta }$ is isomorphic to
$\widetilde {\Theta }/p\widetilde {\Theta }$ is isomorphic to  $\overline {W}_{\chi,3}:=W_{\chi,3}/(\chi \alpha ^2\oplus \chi \alpha ^{-2})$.
$\overline {W}_{\chi,3}:=W_{\chi,3}/(\chi \alpha ^2\oplus \chi \alpha ^{-2})$.
Proof. (i) Note that the cosocle of ![]() $\operatorname {{\mathrm {Ker}}}(r)$ is
$\operatorname {{\mathrm {Ker}}}(r)$ is ![]() $\chi \oplus \chi \alpha ^{-1}$, while that of
$\chi \oplus \chi \alpha ^{-1}$, while that of ![]() $\operatorname {{\mathrm {Ker}}}(r_3)$ is
$\operatorname {{\mathrm {Ker}}}(r_3)$ is ![]() $\chi \alpha$, so the result follows from Lemma 3.4.
$\chi \alpha$, so the result follows from Lemma 3.4.
(ii) It follows from Lemma 3.3 that there are short exact sequences
 \begin{gather*} 0\rightarrow
\operatorname{{\mathrm{Ker}}}(r)/p\operatorname{{\mathrm{Ker}}}(r)\rightarrow
\widetilde{\Theta}/p\widetilde{\Theta}\rightarrow
\Theta_3/p\Theta_3\rightarrow0,\\ 0\rightarrow
\Theta_3'/p\Theta_3'\rightarrow
\widetilde{\Theta}/p\widetilde{\Theta}\rightarrow
\Theta/p\Theta\rightarrow0. \end{gather*}
\begin{gather*} 0\rightarrow
\operatorname{{\mathrm{Ker}}}(r)/p\operatorname{{\mathrm{Ker}}}(r)\rightarrow
\widetilde{\Theta}/p\widetilde{\Theta}\rightarrow
\Theta_3/p\Theta_3\rightarrow0,\\ 0\rightarrow
\Theta_3'/p\Theta_3'\rightarrow
\widetilde{\Theta}/p\widetilde{\Theta}\rightarrow
\Theta/p\Theta\rightarrow0. \end{gather*}
Using Proposition 6.5(ii), we deduce that ![]() $\widetilde {\Theta }/p\widetilde {\Theta }$ admits both the nonsplit extensions
$\widetilde {\Theta }/p\widetilde {\Theta }$ admits both the nonsplit extensions ![]() $(\chi \alpha ^{-1}\ \textbf {---}\ \chi )$ and
$(\chi \alpha ^{-1}\ \textbf {---}\ \chi )$ and ![]() $(\chi \alpha \ \textbf {---}\ \chi )$ as quotients. Combining with part (i), this implies that
$(\chi \alpha \ \textbf {---}\ \chi )$ as quotients. Combining with part (i), this implies that ![]() $\widetilde {\Theta }/p\widetilde {\Theta }$ admits a quotient isomorphic to
$\widetilde {\Theta }/p\widetilde {\Theta }$ admits a quotient isomorphic to ![]() $W_{\chi,2}$; let
$W_{\chi,2}$; let ![]() $\operatorname {{\mathrm {Ker}}}$ be the corresponding kernel. Comparing the Jordan–Hölder factors, we have
$\operatorname {{\mathrm {Ker}}}$ be the corresponding kernel. Comparing the Jordan–Hölder factors, we have ![]() $(\operatorname {{\mathrm {Ker}}})^{\rm ss}\cong \chi \oplus \chi$. However, we know
$(\operatorname {{\mathrm {Ker}}})^{\rm ss}\cong \chi \oplus \chi$. However, we know ![]() $\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\chi )=0$ by Proposition 2.13, hence
$\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\chi )=0$ by Proposition 2.13, hence ![]() $\operatorname {{\mathrm {Ker}}} \cong \chi \oplus \chi$. In particular,
$\operatorname {{\mathrm {Ker}}} \cong \chi \oplus \chi$. In particular, ![]() $\widetilde {\Theta }/p\widetilde {\Theta }$ is killed by
$\widetilde {\Theta }/p\widetilde {\Theta }$ is killed by ![]() $\mathfrak {m}_{D}^3$. The last statement is a consequence of Corollary 2.11.
$\mathfrak {m}_{D}^3$. The last statement is a consequence of Corollary 2.11.
6.3 The Gelfand–Kirillov dimension
Assume ![]() $\overline {\rho } := \overline {r}_v(1)$ is of the form (C1) or (C2) in § 4.3. Recall that for any character
$\overline {\rho } := \overline {r}_v(1)$ is of the form (C1) or (C2) in § 4.3. Recall that for any character ![]() $\chi : \mathcal {O}_D^{\times } \to \mathbb {F}^{\times }$, we have constructed
$\chi : \mathcal {O}_D^{\times } \to \mathbb {F}^{\times }$, we have constructed ![]() $\mathcal {L} \in \{\Theta _1, \Theta _2, \Theta _3, \Theta, \widetilde {\Theta }\}$ such that
$\mathcal {L} \in \{\Theta _1, \Theta _2, \Theta _3, \Theta, \widetilde {\Theta }\}$ such that ![]() $\mathrm {cosoc} (\mathcal {L} / p\mathcal {L}) = \chi$. The construction depends on the choice of
$\mathrm {cosoc} (\mathcal {L} / p\mathcal {L}) = \chi$. The construction depends on the choice of ![]() $(a,b)$ in (6.2). From now on, we assume
$(a,b)$ in (6.2). From now on, we assume ![]() $\chi \in W_D(\overline {\rho })$, and make our choice of
$\chi \in W_D(\overline {\rho })$, and make our choice of ![]() $(a,b)$ as follows:
$(a,b)$ as follows:
 \[ \left\{{\begin{array}{@{}ll} (a,b) =
(r,s) & \text{if}\ \chi = \xi^{r}\alpha^{-1} \zeta^{s+1};
\\ (a,b) = (p-3-r,r+s+1) & \text{if}\ \chi = \xi^{pr} \alpha
\zeta^{s+1}; \\ (a,b) = (r - 2,s+1) & \text{if}\ \chi =
\xi^{r} \zeta^{s+1}; \\ (a,b) = (p-1-r,r+s) & \text{if}\
\chi = \xi^{pr} \zeta^{s+1}. \end{array}}\right.
\]
\[ \left\{{\begin{array}{@{}ll} (a,b) =
(r,s) & \text{if}\ \chi = \xi^{r}\alpha^{-1} \zeta^{s+1};
\\ (a,b) = (p-3-r,r+s+1) & \text{if}\ \chi = \xi^{pr} \alpha
\zeta^{s+1}; \\ (a,b) = (r - 2,s+1) & \text{if}\ \chi =
\xi^{r} \zeta^{s+1}; \\ (a,b) = (p-1-r,r+s) & \text{if}\
\chi = \xi^{pr} \zeta^{s+1}. \end{array}}\right.
\]
Let ![]() $\psi _i$ be given by (6.2) for
$\psi _i$ be given by (6.2) for ![]() $i=0,1,2$. Then one may check directly that
$i=0,1,2$. Then one may check directly that ![]() $\psi _i \neq \psi _i^p$. Let
$\psi _i \neq \psi _i^p$. Let ![]() $\tau _i$ be a tame supercuspidal inertial type so that
$\tau _i$ be a tame supercuspidal inertial type so that ![]() $\sigma (\tau _i) = \Theta (\psi _i)$. Let
$\sigma (\tau _i) = \Theta (\psi _i)$. Let ![]() $\psi :F^\times \setminus {\mathbb {A}}_{F,f}^\times \to \mathcal {O}^\times$ be a continuous character as in § 5 satisfying
$\psi :F^\times \setminus {\mathbb {A}}_{F,f}^\times \to \mathcal {O}^\times$ be a continuous character as in § 5 satisfying ![]() $\psi |_{Z_D\cap \mathcal {O}_D^{\times }} = \psi _1|_{Z_D\cap \mathcal {O}_D^{\times }}$. For
$\psi |_{Z_D\cap \mathcal {O}_D^{\times }} = \psi _1|_{Z_D\cap \mathcal {O}_D^{\times }}$. For ![]() $\mathcal {L} \in \{\Theta _1, \Theta _2, \Theta _3, \Theta, \widetilde {\Theta }\}$, let
$\mathcal {L} \in \{\Theta _1, \Theta _2, \Theta _3, \Theta, \widetilde {\Theta }\}$, let ![]() $I_{\mathcal {L} }: = \operatorname {{\mathrm {Ann}}}_{R_{\infty }^{\psi \varepsilon ^{-1}}}(M_{\infty }^B(\mathcal {L}))$ denote the annihilator of
$I_{\mathcal {L} }: = \operatorname {{\mathrm {Ann}}}_{R_{\infty }^{\psi \varepsilon ^{-1}}}(M_{\infty }^B(\mathcal {L}))$ denote the annihilator of ![]() $M_{\infty }^B(\mathcal {L})$ in
$M_{\infty }^B(\mathcal {L})$ in ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$.
$R_{\infty }^{\psi \varepsilon ^{-1}}$.
Let ![]() $R$ be any commutative ring and
$R$ be any commutative ring and ![]() $M$ be an
$M$ be an ![]() $R$-module. Following [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 8.2] we say
$R$-module. Following [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, § 8.2] we say ![]() $M$ is free of rank
$M$ is free of rank ![]() $m$ over its scheme-theoretic support if it is isomorphic to
$m$ over its scheme-theoretic support if it is isomorphic to ![]() $(R/ \operatorname {{\mathrm {Ann}}}_R(M))^m$.
$(R/ \operatorname {{\mathrm {Ann}}}_R(M))^m$.
Proposition 6.7 Assume ![]() $\chi \in W_B(\overline {r})$. Let
$\chi \in W_B(\overline {r})$. Let ![]() $m := \dim _{\mathbb {F}} \operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }} (\chi, \pi ^B(\overline {r}))$. Then the
$m := \dim _{\mathbb {F}} \operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }} (\chi, \pi ^B(\overline {r}))$. Then the ![]() $R_{\infty }^{ \psi \varepsilon ^{-1}}$-module
$R_{\infty }^{ \psi \varepsilon ^{-1}}$-module ![]() $M_{\infty }^B(\Theta _1)$ (respectively,
$M_{\infty }^B(\Theta _1)$ (respectively, ![]() $M_{\infty }^B(\Theta _2)$, respectively,
$M_{\infty }^B(\Theta _2)$, respectively, ![]() $M_{\infty }^B(\Theta _3)$) is free of rank
$M_{\infty }^B(\Theta _3)$) is free of rank ![]() $m$ over its scheme-theoretic support. In particular,
$m$ over its scheme-theoretic support. In particular, ![]() $I_{\Theta _1} = I_{R_1} R_{\infty }^{ \psi \varepsilon ^{-1}}$,
$I_{\Theta _1} = I_{R_1} R_{\infty }^{ \psi \varepsilon ^{-1}}$, ![]() $I_{\Theta _2} = I_{R_2} R_{\infty }^{ \psi \varepsilon ^{-1}}$ and
$I_{\Theta _2} = I_{R_2} R_{\infty }^{ \psi \varepsilon ^{-1}}$ and ![]() $I_{\Theta _3} = I_{R_3} R_{\infty }^{ \psi \varepsilon ^{-1}}$, where
$I_{\Theta _3} = I_{R_3} R_{\infty }^{ \psi \varepsilon ^{-1}}$, where ![]() $I_{R_1}$,
$I_{R_1}$, ![]() $I_{R_2}$ and
$I_{R_2}$ and ![]() $I_{R_3}$ are given in (4.4).
$I_{R_3}$ are given in (4.4).
Proof. Twisting by the cyclotomic character and taking into account the framed variables, we have an isomorphism
where ![]() $R_{\overline {\rho }}^{\psi \varepsilon }( (0,1),\tau _1)$ is a regular local ring by Proposition 4.13. Hence,
$R_{\overline {\rho }}^{\psi \varepsilon }( (0,1),\tau _1)$ is a regular local ring by Proposition 4.13. Hence, ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1))$, as a formal power series ring over
$R_{\infty }^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1))$, as a formal power series ring over ![]() $R_v^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1))$, is also a regular local ring. Since
$R_v^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1))$, is also a regular local ring. Since ![]() $M_{\infty }^B(\Theta _1)$ is finite maximal Cohen–Macaulay over
$M_{\infty }^B(\Theta _1)$ is finite maximal Cohen–Macaulay over ![]() $R_{\infty }^{\psi \varepsilon ^{-1} }( (-1,0),\tau _1(-1))$, the Auslander–Buchsbaum formula implies that
$R_{\infty }^{\psi \varepsilon ^{-1} }( (-1,0),\tau _1(-1))$, the Auslander–Buchsbaum formula implies that ![]() $M_{\infty }^B (\Theta _1)$ is finite free over
$M_{\infty }^B (\Theta _1)$ is finite free over ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1))$ of rank
$R_{\infty }^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1))$ of rank ![]() $m$ and, hence,
$m$ and, hence, ![]() $I_{\Theta _1} = I_{R_1} R^{\psi \varepsilon ^{-1}}_{\infty }$.
$I_{\Theta _1} = I_{R_1} R^{\psi \varepsilon ^{-1}}_{\infty }$.
Assume ![]() $\mathcal {L} \in \{\Theta _2, \Theta _3\}$. Let
$\mathcal {L} \in \{\Theta _2, \Theta _3\}$. Let ![]() $\delta : \mathbb {Q}_p^{\times } \to \mathcal {O}^{\times }$ be the character sending
$\delta : \mathbb {Q}_p^{\times } \to \mathcal {O}^{\times }$ be the character sending ![]() $x\in \mathbb {Q}_p^{\times }\mapsto \mathrm {pr}(x)^{1/2}\in 1+p\mathbb {Z}_p,$ viewed also as a character of
$x\in \mathbb {Q}_p^{\times }\mapsto \mathrm {pr}(x)^{1/2}\in 1+p\mathbb {Z}_p,$ viewed also as a character of ![]() $F^\times \setminus {\mathbb {A}}_{F,f}^\times$. We also view
$F^\times \setminus {\mathbb {A}}_{F,f}^\times$. We also view ![]() $\delta$ as a character of
$\delta$ as a character of ![]() $G_{\mathbb {Q}_p}$, via the local class field theory. Then
$G_{\mathbb {Q}_p}$, via the local class field theory. Then ![]() $(\mathcal {L}\otimes \delta \circ {\rm Nrd})[1/p]$ is a locally algebraic representation of
$(\mathcal {L}\otimes \delta \circ {\rm Nrd})[1/p]$ is a locally algebraic representation of ![]() $\mathcal {O}_{B_v}^{\times }$. By Theorem 4.15 and Lemma 5.4,
$\mathcal {O}_{B_v}^{\times }$. By Theorem 4.15 and Lemma 5.4, ![]() $R_{\infty }^{ \psi \varepsilon ^{-1} }/I_{\mathcal {L}}$ is a regular local ring. We show as above that
$R_{\infty }^{ \psi \varepsilon ^{-1} }/I_{\mathcal {L}}$ is a regular local ring. We show as above that ![]() $M_{\infty }^B (\mathcal {L})$ is finite free over
$M_{\infty }^B (\mathcal {L})$ is finite free over ![]() $R_{\infty }^{\psi \varepsilon ^{-1} }/I_{\mathcal {L}}$ of some rank
$R_{\infty }^{\psi \varepsilon ^{-1} }/I_{\mathcal {L}}$ of some rank ![]() $n$. It follows from Lemma 5.4 and Corollary 4.6 that
$n$. It follows from Lemma 5.4 and Corollary 4.6 that ![]() $I_{\mathcal {L}}$ has the description as in the statement of the proposition. We are left to prove
$I_{\mathcal {L}}$ has the description as in the statement of the proposition. We are left to prove ![]() $n = m$.
$n = m$.
If ![]() $\operatorname {{\mathrm {JH}}}(\mathcal {L}/p \mathcal {L}) \cap W_D(\overline {\rho }) = \{\chi \}$, then
$\operatorname {{\mathrm {JH}}}(\mathcal {L}/p \mathcal {L}) \cap W_D(\overline {\rho }) = \{\chi \}$, then
which is free of rank ![]() $m$ over its scheme-theoretic support. Hence,
$m$ over its scheme-theoretic support. Hence, ![]() $n = m$.
$n = m$.
Now assume both Jordan–Hölder factors of ![]() $\mathcal {L} / p \mathcal {L}$ are in
$\mathcal {L} / p \mathcal {L}$ are in ![]() $W_D(\overline {\rho })$. By Proposition 6.1 this can only happen when
$W_D(\overline {\rho })$. By Proposition 6.1 this can only happen when ![]() $\overline {\rho }$ is absolutely irreducible. We assume
$\overline {\rho }$ is absolutely irreducible. We assume ![]() $\chi = \xi ^{r}\alpha ^{-1} \zeta ^{s+1}$ and
$\chi = \xi ^{r}\alpha ^{-1} \zeta ^{s+1}$ and ![]() $\mathcal {L} = \Theta _3$, the other cases can be handled in the same way. Since
$\mathcal {L} = \Theta _3$, the other cases can be handled in the same way. Since ![]() $\delta \equiv 1\pmod {\varpi }$ and the following discussion only involves
$\delta \equiv 1\pmod {\varpi }$ and the following discussion only involves ![]() $\mathbb {F}$-representations, the twisting by
$\mathbb {F}$-representations, the twisting by ![]() $\delta$ will not change anything.
$\delta$ will not change anything.
Since
Applying the patching functor ![]() $M_{\infty }^B(-)$, we obtain a short exact sequence
$M_{\infty }^B(-)$, we obtain a short exact sequence
where all the modules in the sequence are finite free over their scheme-theoretic support. We must show the modules have the same rank. For this, we use the knowledge on ![]() $\mathrm {GL}_2$-side to study their support.
$\mathrm {GL}_2$-side to study their support.
According to Proposition 3.11, there exists a ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice
$\mathcal {O}$-lattice ![]() $L$ in
$L$ in ![]() $\underline {\mathrm {Sym}}^1 E^2\otimes \Theta (\psi _3)$ such that
$\underline {\mathrm {Sym}}^1 E^2\otimes \Theta (\psi _3)$ such that ![]() $L/pL$ is a nonsplit extension of
$L/pL$ is a nonsplit extension of ![]() $(\sigma _{p-3-r, r+s+2} \ \textbf {---}\ \sigma _{r, s+1})$ by
$(\sigma _{p-3-r, r+s+2} \ \textbf {---}\ \sigma _{r, s+1})$ by ![]() $( \sigma _{p-1-r, r+s+1} \ \textbf {---}\ \sigma _{r-2, s+2} )$. Let
$( \sigma _{p-1-r, r+s+1} \ \textbf {---}\ \sigma _{r-2, s+2} )$. Let ![]() $\sigma ^{\circ }(\tau _1)$ denote the unique (up to homothety)
$\sigma ^{\circ }(\tau _1)$ denote the unique (up to homothety) ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $\Theta (\psi _1)$ so that
$\Theta (\psi _1)$ so that ![]() $\sigma ^{\circ }(\tau _1)/ p \sigma ^{\circ }(\tau _1) = (\sigma _{p-3-r, r+s+2} \ \textbf {---}\ \sigma _{r, s+1})$. Let
$\sigma ^{\circ }(\tau _1)/ p \sigma ^{\circ }(\tau _1) = (\sigma _{p-3-r, r+s+2} \ \textbf {---}\ \sigma _{r, s+1})$. Let ![]() $\tau$ be a tame supercuspidal inertial type so that there is a
$\tau$ be a tame supercuspidal inertial type so that there is a ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice
$\mathcal {O}$-lattice ![]() $\sigma ^{\circ }(\tau )$ of
$\sigma ^{\circ }(\tau )$ of ![]() $\sigma (\tau )$ satisfying
$\sigma (\tau )$ satisfying ![]() $\sigma ^{\circ }(\tau ) / p\sigma ^{\circ }(\tau ) = ( \sigma _{p-1-r, r+s+1} \ \textbf {---}\ \sigma _{r-2, s+2} )$. Applying Paškūnas’ functor
$\sigma ^{\circ }(\tau ) / p\sigma ^{\circ }(\tau ) = ( \sigma _{p-1-r, r+s+1} \ \textbf {---}\ \sigma _{r-2, s+2} )$. Applying Paškūnas’ functor ![]() $M(-)$ in § 4.2.1, we obtain a short exact sequence
$M(-)$ in § 4.2.1, we obtain a short exact sequence
Note that the three ![]() $R_{\overline {\rho }}^{\psi \varepsilon }$-modules in the above short exact sequence are all cyclic by Lemma 4.7 and Remark 4.10. Then by Theorem 4.5 we obtain the following short exact sequence:
$R_{\overline {\rho }}^{\psi \varepsilon }$-modules in the above short exact sequence are all cyclic by Lemma 4.7 and Remark 4.10. Then by Theorem 4.5 we obtain the following short exact sequence:
On the other hand, ![]() $\sigma _{r-2,s+2},\sigma _{p-3-r,r+s+2}\notin W(\overline {\rho })$ and the extension
$\sigma _{r-2,s+2},\sigma _{p-3-r,r+s+2}\notin W(\overline {\rho })$ and the extension ![]() $(\sigma _{p-1-r, r+s+1}\ \textbf {---}\ \sigma _{r, s+1})$ occurs in
$(\sigma _{p-1-r, r+s+1}\ \textbf {---}\ \sigma _{r, s+1})$ occurs in ![]() $L/pL$ by Proposition 3.11. Let
$L/pL$ by Proposition 3.11. Let ![]() $\tau '$ denote a tame inertial type so that
$\tau '$ denote a tame inertial type so that ![]() $\sigma (\tau ')$ is isomorphic to the principal series tame type
$\sigma (\tau ')$ is isomorphic to the principal series tame type ![]() $I([x]^{s+1}, [x]^{r+s+1})$ defined in Proposition 3.6. Let
$I([x]^{s+1}, [x]^{r+s+1})$ defined in Proposition 3.6. Let ![]() $\sigma ^{\circ }(\tau ')$ be the unique (up to homothety)
$\sigma ^{\circ }(\tau ')$ be the unique (up to homothety) ![]() $K$-stable
$K$-stable ![]() $\mathcal {O}$-lattice in
$\mathcal {O}$-lattice in ![]() $I([x]^{s+1}, [x]^{r+s+1})$ such that
$I([x]^{s+1}, [x]^{r+s+1})$ such that ![]() $\sigma ^{\circ }(\tau ')/ p \sigma ^{\circ }(\tau ') = (\sigma _{p-1-r, r+s+1}\ \textbf {---}\ \sigma _{r, s+1})$. Then the short exact sequence (6.7) can be identified with the following short exact sequence:
$\sigma ^{\circ }(\tau ')/ p \sigma ^{\circ }(\tau ') = (\sigma _{p-1-r, r+s+1}\ \textbf {---}\ \sigma _{r, s+1})$. Then the short exact sequence (6.7) can be identified with the following short exact sequence:
The short exact sequence (6.8) becomes
 \begin{align} 0\to R_{\overline{\rho}}^{\psi\varepsilon ,{\rm cr} }( (r+s+1,p+s+1), \mathbf{1}) &\otimes_{\mathcal{O}} \mathbb{F} \to R_{\overline{\rho}}^{\psi\varepsilon}((0,1),\tau') \nonumber\\ &\otimes_{\mathcal{O}} \mathbb{F} \to R_{\overline{\rho}}^{\psi\varepsilon ,{\rm cr}}( (s+1,r+s+2),\mathbf{1}) \otimes_{\mathcal{O}} \mathbb{F} \to 0. \end{align}
\begin{align} 0\to R_{\overline{\rho}}^{\psi\varepsilon ,{\rm cr} }( (r+s+1,p+s+1), \mathbf{1}) &\otimes_{\mathcal{O}} \mathbb{F} \to R_{\overline{\rho}}^{\psi\varepsilon}((0,1),\tau') \nonumber\\ &\otimes_{\mathcal{O}} \mathbb{F} \to R_{\overline{\rho}}^{\psi\varepsilon ,{\rm cr}}( (s+1,r+s+2),\mathbf{1}) \otimes_{\mathcal{O}} \mathbb{F} \to 0. \end{align}
By [Reference Emerton, Gee and SavittEGS15, Theorem 7.2.1] ![]() $R_{\overline {\rho }}^{\psi \varepsilon }( (0,1),\tau ') \otimes _{\mathcal {O}} \mathbb {F}$ is isomorphic to a formal power series ring over
$R_{\overline {\rho }}^{\psi \varepsilon }( (0,1),\tau ') \otimes _{\mathcal {O}} \mathbb {F}$ is isomorphic to a formal power series ring over ![]() $\mathbb {F}[\![ X,Y]\!]/(XY)$, and
$\mathbb {F}[\![ X,Y]\!]/(XY)$, and ![]() $R_{\overline {\rho }}^{\psi \varepsilon,{\rm cr}} ((r+s+1,p+s+1),\mathbf {1})\otimes \mathbb {F}$ (respectively,
$R_{\overline {\rho }}^{\psi \varepsilon,{\rm cr}} ((r+s+1,p+s+1),\mathbf {1})\otimes \mathbb {F}$ (respectively, ![]() $R_{\overline {\rho }}^{\psi \varepsilon, {\rm cr}} ( (s+1,r+s+2), \mathbf {1}) \otimes _{\mathcal {O}} \mathbb {F}$) is the quotient of
$R_{\overline {\rho }}^{\psi \varepsilon, {\rm cr}} ( (s+1,r+s+2), \mathbf {1}) \otimes _{\mathcal {O}} \mathbb {F}$) is the quotient of ![]() $R_{\overline {\rho }}^{\psi \varepsilon }( (0,1),\tau ') \otimes _{\mathcal {O}} \mathbb {F}$ by
$R_{\overline {\rho }}^{\psi \varepsilon }( (0,1),\tau ') \otimes _{\mathcal {O}} \mathbb {F}$ by ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$). Therefore,
$Y$). Therefore, ![]() $\operatorname {{\mathrm {Spec}}} (R^{\psi \varepsilon }_{\overline {\rho }} ((0,2) ,\tau _3) \otimes _{\mathcal {O}} \mathbb {F})$ has two irreducible components. By Lemma 5.4 and Corollary 4.6,
$\operatorname {{\mathrm {Spec}}} (R^{\psi \varepsilon }_{\overline {\rho }} ((0,2) ,\tau _3) \otimes _{\mathcal {O}} \mathbb {F})$ has two irreducible components. By Lemma 5.4 and Corollary 4.6, ![]() $\operatorname {{\mathrm {Spec}}}(( R_{\infty }^{ \psi \varepsilon ^{-1} }/I_{\Theta _3}) \otimes _{\mathcal {O}}\mathbb {F})$ also has two irreducible components.
$\operatorname {{\mathrm {Spec}}}(( R_{\infty }^{ \psi \varepsilon ^{-1} }/I_{\Theta _3}) \otimes _{\mathcal {O}}\mathbb {F})$ also has two irreducible components.
Back to the short exact sequence (6.6). By the discussion of the first paragraph of the proof, ![]() $M_{\infty }^B(\xi ^{r} \zeta ^{s+1})$ and
$M_{\infty }^B(\xi ^{r} \zeta ^{s+1})$ and ![]() $M_{\infty }^B(\xi ^{r}\alpha ^{-1} \zeta ^{s+1})$ are supported on
$M_{\infty }^B(\xi ^{r}\alpha ^{-1} \zeta ^{s+1})$ are supported on ![]() $\operatorname {{\mathrm {Spec}}} (R_{\infty }^{\psi \varepsilon ^{-1}}((-1,0),\tau (-1)) \otimes _{\mathcal {O}} \mathbb {F})$ and
$\operatorname {{\mathrm {Spec}}} (R_{\infty }^{\psi \varepsilon ^{-1}}((-1,0),\tau (-1)) \otimes _{\mathcal {O}} \mathbb {F})$ and ![]() $\operatorname {{\mathrm {Spec}}}(R_{\infty }^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1)) \otimes _{\mathcal {O}} \mathbb {F})$, respectively. Hence,
$\operatorname {{\mathrm {Spec}}}(R_{\infty }^{\psi \varepsilon ^{-1}}( (-1,0),\tau _1(-1)) \otimes _{\mathcal {O}} \mathbb {F})$, respectively. Hence, ![]() $M_{\infty }^B(\xi ^{r} \zeta ^{s+1})$ and
$M_{\infty }^B(\xi ^{r} \zeta ^{s+1})$ and ![]() $M_{\infty }^B(\xi ^{r}\alpha ^{-1} \zeta ^{s+1})$ are supported on different irreducible components of
$M_{\infty }^B(\xi ^{r}\alpha ^{-1} \zeta ^{s+1})$ are supported on different irreducible components of ![]() $\operatorname {{\mathrm {Spec}}}((R_{\infty }^{ \psi \varepsilon ^{-1} }/I_{\Theta _3}) \otimes _{\mathcal {O}}\mathbb {F})$. We deduce that
$\operatorname {{\mathrm {Spec}}}((R_{\infty }^{ \psi \varepsilon ^{-1} }/I_{\Theta _3}) \otimes _{\mathcal {O}}\mathbb {F})$. We deduce that
 \begin{align} {\rm rank}_{R_{\infty}^{ \psi\varepsilon^{-1} }((-1,0),\tau_1(-1)) \otimes_{\mathcal{O}} \mathbb{F}} (M_{\infty}^B(\xi^{r}\alpha^{-1} \zeta^{s+1})) &= {\rm rank}_{R_{\infty}^{ \psi\varepsilon^{-1}}((-1,0),\tau(-1)) \otimes_{\mathcal{O}} \mathbb{F}} (M_{\infty}^B(\xi^{r} \zeta^{s+1})) \nonumber\\ &= {\rm rank}_{(R_{\infty}^{ \psi\varepsilon^{-1} }/I_{\Theta_3}) \otimes_{\mathcal{O}}\mathbb{F}} (M_{\infty}^B(\Theta_3 / p \Theta_3)). \end{align}
\begin{align} {\rm rank}_{R_{\infty}^{ \psi\varepsilon^{-1} }((-1,0),\tau_1(-1)) \otimes_{\mathcal{O}} \mathbb{F}} (M_{\infty}^B(\xi^{r}\alpha^{-1} \zeta^{s+1})) &= {\rm rank}_{R_{\infty}^{ \psi\varepsilon^{-1}}((-1,0),\tau(-1)) \otimes_{\mathcal{O}} \mathbb{F}} (M_{\infty}^B(\xi^{r} \zeta^{s+1})) \nonumber\\ &= {\rm rank}_{(R_{\infty}^{ \psi\varepsilon^{-1} }/I_{\Theta_3}) \otimes_{\mathcal{O}}\mathbb{F}} (M_{\infty}^B(\Theta_3 / p \Theta_3)). \end{align}
Consequently ![]() $m=n$.
$m=n$.
Corollary 6.8 For any ![]() $\chi _1, \chi _2 \in W_D(\overline {\rho })$, we have
$\chi _1, \chi _2 \in W_D(\overline {\rho })$, we have
Proof. In view of (6.11), it remains to treat the case ![]() $\chi _2 = \chi _1^p$, equivalently
$\chi _2 = \chi _1^p$, equivalently ![]() $\chi _2$ is equal to the conjugation of
$\chi _2$ is equal to the conjugation of ![]() $\chi _1$ by
$\chi _1$ by ![]() $\varpi _D$. But this is clear since
$\varpi _D$. But this is clear since ![]() $\pi ^B(\overline {r})$ is a representation of
$\pi ^B(\overline {r})$ is a representation of ![]() $D^{\times }$, hence is stable under taking the conjugation by
$D^{\times }$, hence is stable under taking the conjugation by ![]() $\varpi _D$. See also [Reference Gee and SavittGS11, Lemma 2.3] which is based on an observation of Serre.
$\varpi _D$. See also [Reference Gee and SavittGS11, Lemma 2.3] which is based on an observation of Serre.
Theorem 6.9 The ![]() $R_{\infty }^{ \psi \varepsilon ^{-1}}$-module
$R_{\infty }^{ \psi \varepsilon ^{-1}}$-module ![]() $M_{\infty }^B(\widetilde {\Theta })$ is free of rank
$M_{\infty }^B(\widetilde {\Theta })$ is free of rank ![]() $m$ over its scheme-theoretic support with
$m$ over its scheme-theoretic support with ![]() $I_{\widetilde {\Theta }} = I_{\Theta _1}\cap I_{\Theta _2} \cap I_{\Theta _3}$.
$I_{\widetilde {\Theta }} = I_{\Theta _1}\cap I_{\Theta _2} \cap I_{\Theta _3}$.
Proof. We first prove ![]() $M_{\infty }^B(\Theta )$ is free of rank
$M_{\infty }^B(\Theta )$ is free of rank ![]() $m$ over its scheme-theoretic support with
$m$ over its scheme-theoretic support with ![]() $I_{\Theta } = I_{\Theta _1} \cap I_{\Theta _2}$. By the short exact sequence (6.4) and the exactness of the functor
$I_{\Theta } = I_{\Theta _1} \cap I_{\Theta _2}$. By the short exact sequence (6.4) and the exactness of the functor ![]() $M_{\infty }^B(-)$, we have
$M_{\infty }^B(-)$, we have
As for a commutative ring ![]() $A$ and two ideals
$A$ and two ideals ![]() $I_1,I_2 \subset A$,
$I_1,I_2 \subset A$,
by Proposition 6.7 we are reduced to checking
Using Corollary 4.11(i) and Proposition 6.7 again, we have
In particular, we obtain
where the third equality holds by [Reference MatsumuraMat89, Theorem 7.4(ii)] because ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$ is flat over
$R_{\infty }^{\psi \varepsilon ^{-1}}$ is flat over ![]() $R_{\overline {\rho }}^{\psi \varepsilon }$.
$R_{\overline {\rho }}^{\psi \varepsilon }$.
Now we prove ![]() $M_{\infty }^B(\widetilde {\Theta })$ is free of rank
$M_{\infty }^B(\widetilde {\Theta })$ is free of rank ![]() $m$ over its scheme-theoretic support. Using (6.5) we have similarly
$m$ over its scheme-theoretic support. Using (6.5) we have similarly
and it suffices to check
Corollary 6.10 For any ![]() $\chi \in W_D(\overline {\rho })$, the natural inclusion
$\chi \in W_D(\overline {\rho })$, the natural inclusion
is an isomorphism, where the structure of ![]() $\overline {W}_{\chi, 3 }$ is given in Proposition 6.6.
$\overline {W}_{\chi, 3 }$ is given in Proposition 6.6.
Proof. The mod ![]() $p$ reduction of the lattice
$p$ reduction of the lattice ![]() $\widetilde {\Theta }$ is isomorphic to
$\widetilde {\Theta }$ is isomorphic to ![]() $\overline {W}_{\chi,3}$ by Proposition 6.6. The result then follows from Theorem 6.9.
$\overline {W}_{\chi,3}$ by Proposition 6.6. The result then follows from Theorem 6.9.
The main result of this section is the following.
Theorem 6.11 Maintain all the assumptions we have made on ![]() $F$,
$F$, ![]() $B$, and
$B$, and ![]() $\overline {r}$. Assume
$\overline {r}$. Assume ![]() $\overline {\rho } = \overline {r}_v(1)$ satisfies (C1) or (C2) in § 4.3. Then
$\overline {\rho } = \overline {r}_v(1)$ satisfies (C1) or (C2) in § 4.3. Then ![]() $\dim _{\mathcal {O}_D^{\times }} (\pi ^B (\overline {r})) = 1$.
$\dim _{\mathcal {O}_D^{\times }} (\pi ^B (\overline {r})) = 1$.
Proof. Since ![]() $\pi ^B (\overline {r})$ is of infinite dimension over
$\pi ^B (\overline {r})$ is of infinite dimension over ![]() $\mathbb {F}$ by [Reference Breuil and DiamondBD14, Corollary 3.2.4] (or [Reference ScholzeScho18, Theorem 7.8]),
$\mathbb {F}$ by [Reference Breuil and DiamondBD14, Corollary 3.2.4] (or [Reference ScholzeScho18, Theorem 7.8]), ![]() $\dim _{\mathcal {O}_D^{\times }} (\pi ^B (\overline {r}))$ is at least one. The other inequality follows from Corollaries 6.10 and 2.12.
$\dim _{\mathcal {O}_D^{\times }} (\pi ^B (\overline {r}))$ is at least one. The other inequality follows from Corollaries 6.10 and 2.12.
Remark 6.12 Although we have excluded the case ![]() $r=0$ in (C2), this case (at least when
$r=0$ in (C2), this case (at least when ![]() $B$ is indefinite) can be deduced from the case
$B$ is indefinite) can be deduced from the case ![]() $r=p-3$. The proof uses Scholze's functor introduced in [Reference ScholzeScho18] and the mod
$r=p-3$. The proof uses Scholze's functor introduced in [Reference ScholzeScho18] and the mod ![]() $p$ local–global compatibility (à la Emerton), see Corollary 7.9.
$p$ local–global compatibility (à la Emerton), see Corollary 7.9.
6.4 The graded module  $\operatorname {{\mathrm {gr}}}(\pi ^B(\overline {r})^{\vee })$
$\operatorname {{\mathrm {gr}}}(\pi ^B(\overline {r})^{\vee })$
Following [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS21, § 3.1], we consider the category ![]() $\mathcal {C}$ of admissible smooth representations
$\mathcal {C}$ of admissible smooth representations ![]() $\pi$ of
$\pi$ of ![]() $D^{\times }$ over
$D^{\times }$ over ![]() $\mathbb {F}$ with a central character and such that there exists a good filtration on the
$\mathbb {F}$ with a central character and such that there exists a good filtration on the ![]() $\pi ^{\vee }$ such that the
$\pi ^{\vee }$ such that the ![]() $\operatorname {{\mathrm {gr}}}\mathbb {F}[\![U_D^1/Z_D^1]\!]$-module
$\operatorname {{\mathrm {gr}}}\mathbb {F}[\![U_D^1/Z_D^1]\!]$-module ![]() $\operatorname {{\mathrm {gr}}} (\pi ^{\vee })$ is annihilated by some power of the ideal
$\operatorname {{\mathrm {gr}}} (\pi ^{\vee })$ is annihilated by some power of the ideal ![]() $(yz,zy)$, where
$(yz,zy)$, where ![]() $y=y_0$,
$y=y_0$, ![]() $z=z_0$ are as in § 2.3.Footnote 6 It is clear that
$z=z_0$ are as in § 2.3.Footnote 6 It is clear that ![]() $\mathcal {C}$ is an abelian category and is stable under subquotients and extensions.
$\mathcal {C}$ is an abelian category and is stable under subquotients and extensions.
Definition 6.13 For each ![]() $\chi \in W_D(\overline {\rho })$, we define an ideal
$\chi \in W_D(\overline {\rho })$, we define an ideal ![]() $\mathfrak {a}(\chi )$ of
$\mathfrak {a}(\chi )$ of ![]() $\mathbb {F}[y,z]$ as follows.
$\mathbb {F}[y,z]$ as follows.
• If
 $\chi \alpha ^{-1}\in W_D(\overline {\rho })$, then
$\chi \alpha ^{-1}\in W_D(\overline {\rho })$, then  $\mathfrak {a}(\chi ):=(y)$; if
$\mathfrak {a}(\chi ):=(y)$; if  $\chi \alpha \in W_D(\overline {\rho })$, then
$\chi \alpha \in W_D(\overline {\rho })$, then  $\mathfrak {a}(\chi ):=(z)$.
$\mathfrak {a}(\chi ):=(z)$.• If neither of
 $\chi \alpha$,
$\chi \alpha$,  $\chi \alpha ^{-1}$ lies in
$\chi \alpha ^{-1}$ lies in  $W_D(\overline {\rho })$, then
$W_D(\overline {\rho })$, then  $\mathfrak {a}(\chi ):=(yz)$.
$\mathfrak {a}(\chi ):=(yz)$.
Theorem 6.14 Maintain all the assumptions we have made on ![]() $F$,
$F$, ![]() $B$ and
$B$ and ![]() $\overline {r}$. Assume
$\overline {r}$. Assume ![]() $\overline {r}_v$ satisfies (C1) or (C2) in § 4.3. Then there exists a surjective graded morphism
$\overline {r}_v$ satisfies (C1) or (C2) in § 4.3. Then there exists a surjective graded morphism
 \[ \bigg(\bigoplus_{\chi\in W_D(\overline{\rho})}\chi^{\vee}\otimes \mathbb{F}[y,z]/\mathfrak{a}(\chi)\bigg)^{\oplus m} \twoheadrightarrow \operatorname{{\mathrm{gr}}}(\pi^B(\overline{r})^{\vee}), \]
\[ \bigg(\bigoplus_{\chi\in W_D(\overline{\rho})}\chi^{\vee}\otimes \mathbb{F}[y,z]/\mathfrak{a}(\chi)\bigg)^{\oplus m} \twoheadrightarrow \operatorname{{\mathrm{gr}}}(\pi^B(\overline{r})^{\vee}), \]
where the integer ![]() $m$ is as in Proposition 6.7.
$m$ is as in Proposition 6.7.
Proof. This is an easy consequence of Corollary 6.10.
7. Application to Scholze's functor
7.1 Results of Scholze and Paškūnas
Let ![]() $L$ be a finite extension of
$L$ be a finite extension of ![]() $\mathbb {Q}_p$,
$\mathbb {Q}_p$, ![]() $G: = \mathrm {GL}_n(L)$ and
$G: = \mathrm {GL}_n(L)$ and ![]() $G_L= \operatorname {{\mathrm {Gal}}}(\overline {L}/L)$. Let
$G_L= \operatorname {{\mathrm {Gal}}}(\overline {L}/L)$. Let ![]() $D$ be the central division algebra over
$D$ be the central division algebra over ![]() $L$ of dimension
$L$ of dimension ![]() $n^2$ and invariant
$n^2$ and invariant ![]() $1/n$. To any
$1/n$. To any ![]() $\pi \in \operatorname {\mathrm {Mod}}_G^{\rm adm}(\mathcal {O})$, Scholze [Reference ScholzeScho18] associated a Weil-equivariant sheaf
$\pi \in \operatorname {\mathrm {Mod}}_G^{\rm adm}(\mathcal {O})$, Scholze [Reference ScholzeScho18] associated a Weil-equivariant sheaf ![]() $\mathcal {F}_{\pi }$ on the étale site of the adic space
$\mathcal {F}_{\pi }$ on the étale site of the adic space ![]() $\mathbb {P}^{n-1}_{\mathbb {C}_p}$. We collect some results of Scholze [Reference ScholzeScho18] and Paškūnas [Reference PaškūnasPaš22].
$\mathbb {P}^{n-1}_{\mathbb {C}_p}$. We collect some results of Scholze [Reference ScholzeScho18] and Paškūnas [Reference PaškūnasPaš22].
Theorem 7.1 Let ![]() $\pi \in \operatorname {\mathrm {Mod}}_{G}^{\rm adm}(\mathcal {O})$.
$\pi \in \operatorname {\mathrm {Mod}}_{G}^{\rm adm}(\mathcal {O})$.
(i) For any
 $i\geq 0$ the étale cohomology group
$i\geq 0$ the étale cohomology group  $H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi })$ carries a continuous
$H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi })$ carries a continuous  $G_L \times D^{\times }$-action. Moreover, the restriction of
$G_L \times D^{\times }$-action. Moreover, the restriction of  $H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi })$ to
$H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi })$ to  $D^{\times }$ is an admissible smooth representation of
$D^{\times }$ is an admissible smooth representation of  $D^{\times }$.
$D^{\times }$.(ii) We have
 $H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$ for
$H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$ for  $i > 2(n-1)$.
$i > 2(n-1)$.(iii) Assume
 $\pi$ admits central character
$\pi$ admits central character  $\psi : Z_G \to \mathbb {F}^{\times }$. If
$\psi : Z_G \to \mathbb {F}^{\times }$. If  $\pi$ is injective in
$\pi$ is injective in  $\operatorname {\mathrm {Mod}}_{\mathrm {GL}_n(\mathcal {O}_L),\psi }^{\rm adm}(\mathcal {O})$, then
$\operatorname {\mathrm {Mod}}_{\mathrm {GL}_n(\mathcal {O}_L),\psi }^{\rm adm}(\mathcal {O})$, then  $H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$ for
$H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$ for  $i > n-1$.
$i > n-1$.(iv) The natural map
is an isomorphism. In particular, if \[ H^0_{\mathrm{\acute{e}t}}(\mathbb{P}^{n-1}_{\mathbb{C}_p}, \mathcal{F}_{\pi^{\mathrm{SL}_n(L)}}) \hookrightarrow H^0_{\mathrm{\acute{e}t}}(\mathbb{P}^{n-1}_{\mathbb{C}_p}, \mathcal{F}_{\pi}) \]
\[ H^0_{\mathrm{\acute{e}t}}(\mathbb{P}^{n-1}_{\mathbb{C}_p}, \mathcal{F}_{\pi^{\mathrm{SL}_n(L)}}) \hookrightarrow H^0_{\mathrm{\acute{e}t}}(\mathbb{P}^{n-1}_{\mathbb{C}_p}, \mathcal{F}_{\pi}) \]
 $\pi ^{\mathrm {SL}_n(L)} = 0$, then
$\pi ^{\mathrm {SL}_n(L)} = 0$, then  $H^0_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$.
$H^0_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$.(v) If
 $\pi = \mathbf {1}_{G}$ is the trivial representation of
$\pi = \mathbf {1}_{G}$ is the trivial representation of  $G$ over
$G$ over  $\mathbb {F}$, then
$\mathbb {F}$, then
 \[
H^i_{\mathrm{\acute{e}t}}(\mathbb{P}^{n-1}_{\mathbb{C}_p},
\mathcal{F}_{\mathbf{1}_G}) = \left\{{\begin{array}{@{}ll}
\omega^{-i/2}\otimes \mathbf{1}_{D^{\times}} & \text{if}\ i\
\text{is even and}\ 0\leq i \leq 2(n-1); \\ 0 & \text{if}\ i\ \text{is
odd.} \end{array}}\right. \]
\[
H^i_{\mathrm{\acute{e}t}}(\mathbb{P}^{n-1}_{\mathbb{C}_p},
\mathcal{F}_{\mathbf{1}_G}) = \left\{{\begin{array}{@{}ll}
\omega^{-i/2}\otimes \mathbf{1}_{D^{\times}} & \text{if}\ i\
\text{is even and}\ 0\leq i \leq 2(n-1); \\ 0 & \text{if}\ i\ \text{is
odd.} \end{array}}\right. \]
Proof. Parts (i) and (ii) are proved in [Reference ScholzeScho18, Theorem 3.2].
For part (iii),Footnote 7 it is proved in [Reference ScholzeScho18, Theorem 3.2] that if ![]() $\pi \in \operatorname {\mathrm {Mod}}_{G}^{\rm adm}(\mathcal {O})$ such that
$\pi \in \operatorname {\mathrm {Mod}}_{G}^{\rm adm}(\mathcal {O})$ such that ![]() $\pi |_{\mathrm {GL}_n(\mathcal {O}_L)}$ is injective, then
$\pi |_{\mathrm {GL}_n(\mathcal {O}_L)}$ is injective, then ![]() $H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$ for
$H^i_{\mathrm {\acute {e}t}}(\mathbb {P}^{n-1}_{\mathbb {C}_p}, \mathcal {F}_{\pi }) = 0$ for ![]() $i > n-1$. We need to prove a similar result for
$i > n-1$. We need to prove a similar result for ![]() $\pi$ which admits a central character. Twisting by a character, we may assume the central character of
$\pi$ which admits a central character. Twisting by a character, we may assume the central character of ![]() $\pi$ is trivial. Examining the proof of [Reference ScholzeScho18, Theorem 3.2], it suffices to show that
$\pi$ is trivial. Examining the proof of [Reference ScholzeScho18, Theorem 3.2], it suffices to show that ![]() $\mathcal {M}_{\infty }/L^{\times }$ is a perfectoid space, where
$\mathcal {M}_{\infty }/L^{\times }$ is a perfectoid space, where ![]() $\mathcal {M}_{\infty }$ is the infinite level Lubin–Tate space. Passing to the connected components, it suffices to show that
$\mathcal {M}_{\infty }$ is the infinite level Lubin–Tate space. Passing to the connected components, it suffices to show that ![]() $\mathcal {M}^{(0)}_{\infty }/\mathcal {O}_L^{\times }$ is a perfectoid space, where
$\mathcal {M}^{(0)}_{\infty }/\mathcal {O}_L^{\times }$ is a perfectoid space, where ![]() $\mathcal {M}^{(0)}_{\infty }$ is the perfectoid space denoted by
$\mathcal {M}^{(0)}_{\infty }$ is the perfectoid space denoted by ![]() $\mathcal {M}^{(0)}_{\bf 1}$ in [Reference Johansson, Ludwig and HansenJLH21, § 4.1]. We will deduce this from [Reference Johansson, Ludwig and HansenJLH21, Proposition 4.1.1] which proves that
$\mathcal {M}^{(0)}_{\bf 1}$ in [Reference Johansson, Ludwig and HansenJLH21, § 4.1]. We will deduce this from [Reference Johansson, Ludwig and HansenJLH21, Proposition 4.1.1] which proves that ![]() $\mathcal {M}^{(0)}_{\infty }/P(\mathcal {O}_L)$ is a perfectoid space, where
$\mathcal {M}^{(0)}_{\infty }/P(\mathcal {O}_L)$ is a perfectoid space, where ![]() $P\subset \mathrm {GL}_n$ is the parabolic subgroup of block form
$P\subset \mathrm {GL}_n$ is the parabolic subgroup of block form ![]() $(n-1,1)$.
$(n-1,1)$.
We use freely the notation of [Reference Johansson, Ludwig and HansenJLH21, § 4.1]. Note that ![]() $\mathcal {M}_{\infty }$ is denoted by
$\mathcal {M}_{\infty }$ is denoted by ![]() $\mathcal {M}_{\bf 1}$ in [Reference Johansson, Ludwig and HansenJLH21, § 4.1]. Let
$\mathcal {M}_{\bf 1}$ in [Reference Johansson, Ludwig and HansenJLH21, § 4.1]. Let ![]() $H\subseteq \mathrm {GL}_n(\mathcal {O}_L)$ be a closed subgroup. As in [Reference Johansson, Ludwig and HansenJLH21, § 4.1], we set
$H\subseteq \mathrm {GL}_n(\mathcal {O}_L)$ be a closed subgroup. As in [Reference Johansson, Ludwig and HansenJLH21, § 4.1], we set
where ![]() $U$ ranges over open subgroups of
$U$ ranges over open subgroups of ![]() $\mathrm {GL}_n(\mathcal {O}_L)$ containing
$\mathrm {GL}_n(\mathcal {O}_L)$ containing ![]() $H$. By [Reference Johansson, Ludwig and HansenJLH21, Proposition 4.1.1],
$H$. By [Reference Johansson, Ludwig and HansenJLH21, Proposition 4.1.1], ![]() $\mathcal {M}^{(0)}_{P(\mathcal {O}_L)}$ is the quotient
$\mathcal {M}^{(0)}_{P(\mathcal {O}_L)}$ is the quotient ![]() $\mathcal {M}^{(0)}_{\infty }/ P(\mathcal {O}_L)$ in Huber's category
$\mathcal {M}^{(0)}_{\infty }/ P(\mathcal {O}_L)$ in Huber's category ![]() $\mathcal {V}$, and is a perfectoid space. Now assume
$\mathcal {V}$, and is a perfectoid space. Now assume ![]() $H\subset \mathrm {GL}_n(\mathcal {O}_L)$ is a closed subgroup contained in
$H\subset \mathrm {GL}_n(\mathcal {O}_L)$ is a closed subgroup contained in ![]() $P(\mathcal {O}_L)$. The same argument as in the proof of [Reference Johansson, Ludwig and HansenJLH21, Proposition 3.2.1] shows that
$P(\mathcal {O}_L)$. The same argument as in the proof of [Reference Johansson, Ludwig and HansenJLH21, Proposition 3.2.1] shows that ![]() $\mathcal {M}^{(0)}_{H}$ is a perfectoid space. More precisely, if
$\mathcal {M}^{(0)}_{H}$ is a perfectoid space. More precisely, if ![]() $H$ is of finite index in
$H$ is of finite index in ![]() $P(\mathcal {O}_L)$, then
$P(\mathcal {O}_L)$, then ![]() $\mathcal {M}^{(0)}_{H}$ is finite étale over
$\mathcal {M}^{(0)}_{H}$ is finite étale over ![]() $\mathcal {M}^{(0)}_{P(\mathcal {O}_L)}$, and the result then follows. In general,
$\mathcal {M}^{(0)}_{P(\mathcal {O}_L)}$, and the result then follows. In general, ![]() $\mathcal {M}^{(0)}_{H} = \varprojlim _{H'} \mathcal {M}^{(0)}_{H'}$ where
$\mathcal {M}^{(0)}_{H} = \varprojlim _{H'} \mathcal {M}^{(0)}_{H'}$ where ![]() $H'$ ranges over closed subgroups with
$H'$ ranges over closed subgroups with ![]() $H\subseteq H' \subseteq P(\mathcal {O}_L)$ and
$H\subseteq H' \subseteq P(\mathcal {O}_L)$ and ![]() $H'\subseteq P(\mathcal {O}_L)$ has finite index, and the result follows. We can then argue as in the proof of [Reference Johansson, Ludwig and HansenJLH21, Lemma 3.3.4] to prove that
$H'\subseteq P(\mathcal {O}_L)$ has finite index, and the result follows. We can then argue as in the proof of [Reference Johansson, Ludwig and HansenJLH21, Lemma 3.3.4] to prove that ![]() $\mathcal {M}^{(0)}_{\infty }$ is an
$\mathcal {M}^{(0)}_{\infty }$ is an ![]() $H$-torsor over
$H$-torsor over ![]() $\mathcal {M}^{(0)}_{H}$. Finally, it follows from [Reference Johansson, Ludwig and HansenJLH21, Lemma 3.3.5] that
$\mathcal {M}^{(0)}_{H}$. Finally, it follows from [Reference Johansson, Ludwig and HansenJLH21, Lemma 3.3.5] that ![]() $\mathcal {M}^{(0)}_{H}$ is the quotient
$\mathcal {M}^{(0)}_{H}$ is the quotient ![]() $\mathcal {M}^{(0)}_{\infty }/ H$ in Huber's category
$\mathcal {M}^{(0)}_{\infty }/ H$ in Huber's category ![]() $\mathcal {V}$. We finish the proof by taking
$\mathcal {V}$. We finish the proof by taking ![]() $H = \mathcal {O}_L^{\times }$.
$H = \mathcal {O}_L^{\times }$.
Part (iv) is proved in [Reference ScholzeScho18, Proposition 4.7]. For part (v), we note that ![]() $\mathcal {F}_{\mathbf {1}_G}$ is the trivial local system on
$\mathcal {F}_{\mathbf {1}_G}$ is the trivial local system on ![]() $\mathbb {P}^{n-1}_{\mathbb {C}_p}$. It follows from [Reference HuberHub96, Theorem 3.8.1] that the cohomology of
$\mathbb {P}^{n-1}_{\mathbb {C}_p}$. It follows from [Reference HuberHub96, Theorem 3.8.1] that the cohomology of ![]() $\mathbb {P}^{n-1}_{\mathbb {C}_p}$ (with the Galois action) is as in the classical case. As
$\mathbb {P}^{n-1}_{\mathbb {C}_p}$ (with the Galois action) is as in the classical case. As ![]() $D^{\times }$ acts on
$D^{\times }$ acts on ![]() $\mathbb {P}^{n-1}_{\mathbb {C}_p}$ via an embedding
$\mathbb {P}^{n-1}_{\mathbb {C}_p}$ via an embedding ![]() $D^{\times }\hookrightarrow \mathrm {GL}_n(L^{\rm un})$,
$D^{\times }\hookrightarrow \mathrm {GL}_n(L^{\rm un})$, ![]() $D^{\times }$ acts trivially on the cohomology.
$D^{\times }$ acts trivially on the cohomology.
Let ![]() $\pi$ be a locally admissible
$\pi$ be a locally admissible ![]() $\mathcal {O}$-torsion representation of
$\mathcal {O}$-torsion representation of ![]() $G$. The construction of the sheaf
$G$. The construction of the sheaf ![]() $\mathcal {F}_{\pi }$ in [Reference ScholzeScho18, Proposition 3.1] extends to such
$\mathcal {F}_{\pi }$ in [Reference ScholzeScho18, Proposition 3.1] extends to such ![]() $\pi$. Write
$\pi$. Write ![]() $\pi = \varinjlim _{\pi '} \pi '$, where the limit is taken over all admissible subrepresentations of
$\pi = \varinjlim _{\pi '} \pi '$, where the limit is taken over all admissible subrepresentations of ![]() $\pi$. By [Reference PaškūnasPaš22, (9)], we have
$\pi$. By [Reference PaškūnasPaš22, (9)], we have
We denote by ![]() $\mathcal {S}^i$ the cohomological covariant
$\mathcal {S}^i$ the cohomological covariant ![]() $\delta$-functor
$\delta$-functor
where ![]() $\operatorname {\mathrm {Mod}}_{G_{L}\times D^{\times }}^{\rm l.adm}(\mathcal {O})$ is the category of locally admissible representations of
$\operatorname {\mathrm {Mod}}_{G_{L}\times D^{\times }}^{\rm l.adm}(\mathcal {O})$ is the category of locally admissible representations of ![]() $D^{\times }$ on
$D^{\times }$ on ![]() $\mathcal {O}$-torsion modules equipped with a continuous commuting
$\mathcal {O}$-torsion modules equipped with a continuous commuting ![]() $G_{L}$-action. As in [Reference PaškūnasPaš22], it is more convenient to work on pseudo-compact modules rather than smooth representations via the Pontryagin duality. Namely, we consider the covariant homological
$G_{L}$-action. As in [Reference PaškūnasPaš22], it is more convenient to work on pseudo-compact modules rather than smooth representations via the Pontryagin duality. Namely, we consider the covariant homological ![]() $\delta$-functor
$\delta$-functor ![]() $\{\check {\mathcal {S}}^i \}_{i \geq 0}$ defined by
$\{\check {\mathcal {S}}^i \}_{i \geq 0}$ defined by
If ![]() $R$ is a complete local noetherian
$R$ is a complete local noetherian ![]() $\mathcal {O}$-algebra with residue field
$\mathcal {O}$-algebra with residue field ![]() $\mathbb {F}$, we extend the
$\mathbb {F}$, we extend the ![]() $\delta$-functor
$\delta$-functor ![]() $\check {\mathcal {S}}^i$ to
$\check {\mathcal {S}}^i$ to ![]() $\frak {C}_G(R)$ (defined in § 4.4) in a similar way.
$\frak {C}_G(R)$ (defined in § 4.4) in a similar way.
7.2 Local–global compatibility (à la Scholze)
From now on, we follow the notation of § 5. Let ![]() $B$ be an indefinite quaternion algebra over the totally field
$B$ be an indefinite quaternion algebra over the totally field ![]() $F$ such that
$F$ such that ![]() $B$ is ramified at the fixed place
$B$ is ramified at the fixed place ![]() $v$ above
$v$ above ![]() $p$. Let
$p$. Let ![]() $B'$ be the definite quaternion algebra over
$B'$ be the definite quaternion algebra over ![]() $F$ which splits at
$F$ which splits at ![]() $v$ and has the same ramification behavior as
$v$ and has the same ramification behavior as ![]() $B$ at all the other finite places. Fix an isomorphism
$B$ at all the other finite places. Fix an isomorphism ![]() $B^{\times }(\mathbb {A}_{F,f}^{v}) \cong B'^{\times }(\mathbb {A}_{F,f}^{v})$. Fix an open compact subgroup
$B^{\times }(\mathbb {A}_{F,f}^{v}) \cong B'^{\times }(\mathbb {A}_{F,f}^{v})$. Fix an open compact subgroup ![]() $U^{v}\subset B^{\times }(\mathbb {A}_{F,f}^{v}) \cong B'^{\times }(\mathbb {A}_{F,f}^{v})$. Let
$U^{v}\subset B^{\times }(\mathbb {A}_{F,f}^{v}) \cong B'^{\times }(\mathbb {A}_{F,f}^{v})$. Let ![]() $\overline {r} : G_{F} \to \mathrm {GL}_2(\mathbb {F})$ be a modular Galois representation and let
$\overline {r} : G_{F} \to \mathrm {GL}_2(\mathbb {F})$ be a modular Galois representation and let ![]() $\frak {m}_{\overline {r}}$ be the non-Eisenstein maximal ideal associated to
$\frak {m}_{\overline {r}}$ be the non-Eisenstein maximal ideal associated to ![]() $\overline {r}$ as in § 5. Let
$\overline {r}$ as in § 5. Let ![]() $\sigma _p^{v}$ be the finite
$\sigma _p^{v}$ be the finite ![]() $\mathcal {O}[\![U^{v}]\!]$-module as in (5.1). If
$\mathcal {O}[\![U^{v}]\!]$-module as in (5.1). If ![]() $A$ is a topological
$A$ is a topological ![]() $\mathcal {O}$-algebra, let
$\mathcal {O}$-algebra, let
 \begin{align*} \widetilde{S}_{\sigma_p^v, \psi} (U^{v} , A) &:= \widetilde{H}^{0,B'}_{\sigma_p^v , \psi} (U^{v}, \mathcal{O}) \otimes_{\mathcal{O}} A,\\ \widetilde{H}^i_{\sigma_p^{v}, \psi} (U^{v} , A) &:= \widetilde{H}^{i,B}_{\sigma_p^v , \psi} (U^{v}, \mathcal{O}) \otimes_{\mathcal{O}} A,\quad i\geq 0. \end{align*}
\begin{align*} \widetilde{S}_{\sigma_p^v, \psi} (U^{v} , A) &:= \widetilde{H}^{0,B'}_{\sigma_p^v , \psi} (U^{v}, \mathcal{O}) \otimes_{\mathcal{O}} A,\\ \widetilde{H}^i_{\sigma_p^{v}, \psi} (U^{v} , A) &:= \widetilde{H}^{i,B}_{\sigma_p^v , \psi} (U^{v}, \mathcal{O}) \otimes_{\mathcal{O}} A,\quad i\geq 0. \end{align*}
The Hecke algebra ![]() ${\mathbb {T}}(U^v)_{\frak {m}_{\overline {r}}}$ acts faithfully and continuously on
${\mathbb {T}}(U^v)_{\frak {m}_{\overline {r}}}$ acts faithfully and continuously on ![]() $\widetilde {S}_{\sigma _p^v, \psi } (U^{v}, \mathcal {O})_{\frak {m}_{\overline {r}}}$ and
$\widetilde {S}_{\sigma _p^v, \psi } (U^{v}, \mathcal {O})_{\frak {m}_{\overline {r}}}$ and ![]() $\widetilde {H}^i_{\sigma _p^{v}, \psi } (U^{v}, \mathcal {O})_{\frak {m}_{\overline {r}}}$ (see [Reference ScholzeScho18, Corollary 7.3]).
$\widetilde {H}^i_{\sigma _p^{v}, \psi } (U^{v}, \mathcal {O})_{\frak {m}_{\overline {r}}}$ (see [Reference ScholzeScho18, Corollary 7.3]).
Let ![]() $M_{\infty }$ denote the big patched module
$M_{\infty }$ denote the big patched module ![]() $M_{\infty }^{B'}$ in § 5, so that
$M_{\infty }^{B'}$ in § 5, so that
where ![]() $\mathfrak {a}_{\infty }$ denotes the ideal
$\mathfrak {a}_{\infty }$ denotes the ideal ![]() $(z_1,\ldots,z_q,y_1,\ldots,y_j)$ of
$(z_1,\ldots,z_q,y_1,\ldots,y_j)$ of ![]() $S_{\infty }$ and
$S_{\infty }$ and ![]() $\mathfrak {m}_{\infty }$ denotes the maximal ideal of
$\mathfrak {m}_{\infty }$ denotes the maximal ideal of ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$.
$R_{\infty }^{\psi \varepsilon ^{-1}}$.
On the other hand, let ![]() $N_{\infty }$ be the variant of
$N_{\infty }$ be the variant of ![]() $M_{\infty }^B$ which is obtained by the same patching process as
$M_{\infty }^B$ which is obtained by the same patching process as ![]() $M_{\infty }^{B}$, but without ‘factorizing out’ the Galois representation, see Remark 5.2. Similarly to (5.2) we have
$M_{\infty }^{B}$, but without ‘factorizing out’ the Galois representation, see Remark 5.2. Similarly to (5.2) we have
Theorem 7.2 Denote the restriction of ![]() $\psi$ to
$\psi$ to ![]() $F_v^{\times }$ again by
$F_v^{\times }$ again by ![]() $\psi$. Let
$\psi$. Let ![]() $G := \mathrm{GL}_2 (F_v)$.
$G := \mathrm{GL}_2 (F_v)$.
(i) We have that
 $\widetilde {S}_{\sigma _p^v,\psi }(U^{v}, E/\mathcal {O})_{\frak {m}_{\overline {r}}}$ lies in
$\widetilde {S}_{\sigma _p^v,\psi }(U^{v}, E/\mathcal {O})_{\frak {m}_{\overline {r}}}$ lies in  $\operatorname {\mathrm {Mod}}_{G,\psi }^{\rm adm}(\mathcal {O})$, and its restriction to
$\operatorname {\mathrm {Mod}}_{G,\psi }^{\rm adm}(\mathcal {O})$, and its restriction to  $K:= \mathrm {GL}_2(\mathcal {O}_{F_v})$ is injective in
$K:= \mathrm {GL}_2(\mathcal {O}_{F_v})$ is injective in  $\operatorname {\mathrm {Mod}}_{K,\psi }^{\rm sm}(\mathcal {O})$. Equivalently by taking dual,
$\operatorname {\mathrm {Mod}}_{K,\psi }^{\rm sm}(\mathcal {O})$. Equivalently by taking dual,  $\widetilde {S}_{\sigma _p^v ,\psi }(U^{v} , \mathcal {O})^d_{\frak {m}_{\overline {r}}}$ is finitely generated over
$\widetilde {S}_{\sigma _p^v ,\psi }(U^{v} , \mathcal {O})^d_{\frak {m}_{\overline {r}}}$ is finitely generated over  $\mathcal {O}[\![K]\!]$ and is projective in
$\mathcal {O}[\![K]\!]$ and is projective in  $\operatorname {\mathrm {Mod}}_{K,\psi }^{\rm pro}(\mathcal {O})$.
$\operatorname {\mathrm {Mod}}_{K,\psi }^{\rm pro}(\mathcal {O})$.(ii) We have that
 $\widetilde {H}^1_{\sigma _p^v, \psi } (U^{v} , E / \mathcal {O})_{\frak {m}_{\overline {r}}}$ lies in
$\widetilde {H}^1_{\sigma _p^v, \psi } (U^{v} , E / \mathcal {O})_{\frak {m}_{\overline {r}}}$ lies in  $\operatorname {\mathrm {Mod}}_{D^{\times },\psi }^{\rm adm}(\mathcal {O})$, and its restriction to
$\operatorname {\mathrm {Mod}}_{D^{\times },\psi }^{\rm adm}(\mathcal {O})$, and its restriction to  $\mathcal {O}_{D}^{\times }$ is injective in
$\mathcal {O}_{D}^{\times }$ is injective in  $\operatorname {\mathrm {Mod}}_{ \mathcal {O}_{D}^{\times },\psi }^{\rm sm}(\mathcal {O})$. Equivalently,
$\operatorname {\mathrm {Mod}}_{ \mathcal {O}_{D}^{\times },\psi }^{\rm sm}(\mathcal {O})$. Equivalently,  $\widetilde {H}^1_{\sigma _p^v, \psi } (U^{v}, \mathcal {O})^d_{\frak {m}_{\overline {r}}}$ is a finitely generated
$\widetilde {H}^1_{\sigma _p^v, \psi } (U^{v}, \mathcal {O})^d_{\frak {m}_{\overline {r}}}$ is a finitely generated  $\mathcal {O}[\![\mathcal {O}_{D}^{\times }]\!]$-module and is projective in
$\mathcal {O}[\![\mathcal {O}_{D}^{\times }]\!]$-module and is projective in  $\operatorname {\mathrm {Mod}}_{\mathcal {O}_{D}^{\times } ,\psi }^{\rm pro}(\mathcal {O})$.
$\operatorname {\mathrm {Mod}}_{\mathcal {O}_{D}^{\times } ,\psi }^{\rm pro}(\mathcal {O})$.(iii) For
 $0\leq i\leq 2$, there is a canonical isomorphism of
$0\leq i\leq 2$, there is a canonical isomorphism of  ${\mathbb {T}}(U^{v})_{\frak {m}_{\overline {r}}}[G_{F_v} \times D^{\times }]$-modules
${\mathbb {T}}(U^{v})_{\frak {m}_{\overline {r}}}[G_{F_v} \times D^{\times }]$-modules
 \[ \check{\mathcal{S}}^i (\widetilde{S}_{\sigma_p^v, \psi}(U^{v} , \mathcal{O})^d_{\frak{m}_{\overline{r}}}) \cong \widetilde{H}^i_{\sigma_p^v, \psi} (U^{v} , \mathcal{O})^d_{\frak{m}_{\overline{r}}}. \]
\[ \check{\mathcal{S}}^i (\widetilde{S}_{\sigma_p^v, \psi}(U^{v} , \mathcal{O})^d_{\frak{m}_{\overline{r}}}) \cong \widetilde{H}^i_{\sigma_p^v, \psi} (U^{v} , \mathcal{O})^d_{\frak{m}_{\overline{r}}}. \]
(iv) There is a canonical
 $R_{\infty }^{\psi \varepsilon ^{-1}}[G_{F_{v}} \times D^{\times }]$-equivariant isomorphism
$R_{\infty }^{\psi \varepsilon ^{-1}}[G_{F_{v}} \times D^{\times }]$-equivariant isomorphism
 \[ \check{\mathcal{S}}^1 ( M_{\infty} ) = N_{\infty}. \]
\[ \check{\mathcal{S}}^1 ( M_{\infty} ) = N_{\infty}. \]
Proof. Part (i) is [Reference PaškūnasPaš22, Lemma 5.3, Proposition 5.4]. Part (ii) is proved in [Reference NewtonNew13, Proposition 5.6] and [Reference PaškūnasPaš22, Proposition 6.4]. Part (iii) is [Reference PaškūnasPaš22, Proposition 6.3]. Part (iv) follows from (the proof of) [Reference ScholzeScho18, Corollary 9.3], see [Reference Dospinescu, Paškūnas and SchraenDPS23, Theorem 8.10 (4)] for details.
Lemma 7.3 We have ![]() $\check {\mathcal {S}}^0(\widetilde {S}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O})^d_{\frak {m}_{\overline {r}}})=0$ and
$\check {\mathcal {S}}^0(\widetilde {S}_{\sigma _p^v , \psi } (U^{v}, \mathcal {O})^d_{\frak {m}_{\overline {r}}})=0$ and ![]() $\check {\mathcal {S}}^0(M_{\infty })=0$.
$\check {\mathcal {S}}^0(M_{\infty })=0$.
Proof. The first statement is a direct consequence of Theorem 7.2(iii) because ![]() $\widetilde {H}^0_{\sigma _p^v, \psi } (U^{v} , \mathcal {O})^d_{\frak {m}_{\overline {r}}}=0$ (as
$\widetilde {H}^0_{\sigma _p^v, \psi } (U^{v} , \mathcal {O})^d_{\frak {m}_{\overline {r}}}=0$ (as ![]() $\frak {m}_{\overline {r}}$ is non-Eisenstein). The second statement follows from this and the patching construction (cf. [Reference ScholzeScho18, Corollary 9.3]).
$\frak {m}_{\overline {r}}$ is non-Eisenstein). The second statement follows from this and the patching construction (cf. [Reference ScholzeScho18, Corollary 9.3]).
Define
Note that ![]() $(N_{\infty }/\mathfrak {m}_{\infty })^{\vee }$ is
$(N_{\infty }/\mathfrak {m}_{\infty })^{\vee }$ is ![]() $\overline {r}$-typic, so we have a
$\overline {r}$-typic, so we have a ![]() $G_{F}\times D^{\times }$-equivariant isomorphism
$G_{F}\times D^{\times }$-equivariant isomorphism ![]() $(N_{\infty }/\mathfrak {m}_{\infty })^{\vee }\cong \overline {r}\otimes \pi ^B(\overline {r})$. The following result is motivated by [Reference PaškūnasPaš22, Propositions 3.7, 4.1].
$(N_{\infty }/\mathfrak {m}_{\infty })^{\vee }\cong \overline {r}\otimes \pi ^B(\overline {r})$. The following result is motivated by [Reference PaškūnasPaš22, Propositions 3.7, 4.1].
Proposition 7.4 Assume that ![]() $R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth and that
$R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth and that ![]() $\dim _{K}(\pi ^{B'}(\overline {r}))=[F_v:\mathbb {Q}_p]$. Then
$\dim _{K}(\pi ^{B'}(\overline {r}))=[F_v:\mathbb {Q}_p]$. Then ![]() $M_{\infty }$ is a flat
$M_{\infty }$ is a flat ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$-module. Moreover, the following statements are equivalent:
$R_{\infty }^{\psi \varepsilon ^{-1}}$-module. Moreover, the following statements are equivalent:
(i)
 $\dim _{\mathcal {O}_D^{\times }} (\pi ^B (\overline {r})) = [F_v:\mathbb {Q}_p]$;
$\dim _{\mathcal {O}_D^{\times }} (\pi ^B (\overline {r})) = [F_v:\mathbb {Q}_p]$;(ii)
 $N_{\infty }$ is flat over
$N_{\infty }$ is flat over  $R_{\infty }^{\psi \varepsilon ^{-1}}$;
$R_{\infty }^{\psi \varepsilon ^{-1}}$;(iii)
 $\mathcal {S}^2 (\pi ^{B'} (\overline {r}) ) = 0$.
$\mathcal {S}^2 (\pi ^{B'} (\overline {r}) ) = 0$.
Proof. Since ![]() $R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth by assumption, it is isomorphic to a power series ring in
$R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth by assumption, it is isomorphic to a power series ring in ![]() $(3 + 3[F_v:\mathbb {Q}_p])$-variables over
$(3 + 3[F_v:\mathbb {Q}_p])$-variables over ![]() $\mathcal {O}$. Consequently,
$\mathcal {O}$. Consequently, ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$ is a regular local ring of Krull dimension equal to
$R_{\infty }^{\psi \varepsilon ^{-1}}$ is a regular local ring of Krull dimension equal to ![]() $\dim S_{\infty } + 2 [F_v : \mathbb {Q}_p]$.
$\dim S_{\infty } + 2 [F_v : \mathbb {Q}_p]$.
Since ![]() $M_{\infty }$ is finite projective over
$M_{\infty }$ is finite projective over ![]() $S_{\infty }[\![K/Z_1]\!]$, where
$S_{\infty }[\![K/Z_1]\!]$, where ![]() $Z_1$ is the centre of
$Z_1$ is the centre of ![]() $K_1$,
$K_1$, ![]() $\delta _{S_{\infty }[\![K]\!]}(M_{\infty }) = \dim S_{\infty } + \dim _{\mathbb {Q}_p} (K/Z_1)$ by [Reference Gee and NewtonGN22, Lemma A.15], see § 1.1 for the notation. Since
$\delta _{S_{\infty }[\![K]\!]}(M_{\infty }) = \dim S_{\infty } + \dim _{\mathbb {Q}_p} (K/Z_1)$ by [Reference Gee and NewtonGN22, Lemma A.15], see § 1.1 for the notation. Since ![]() $\dim _{\mathbb {Q}_p}(K/Z_1)=3[F_v:\mathbb {Q}_p]$ and
$\dim _{\mathbb {Q}_p}(K/Z_1)=3[F_v:\mathbb {Q}_p]$ and ![]() $\dim _K(\pi ^{B'}(\overline {r}))=[F_v:\mathbb {Q}_p]$ by assumption, we deduce
$\dim _K(\pi ^{B'}(\overline {r}))=[F_v:\mathbb {Q}_p]$ by assumption, we deduce
It follows from the miracle flatness criterion [Reference Gee and NewtonGN22, Proposition A.30] that ![]() $M_{\infty }$ is flat over
$M_{\infty }$ is flat over ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$.
$R_{\infty }^{\psi \varepsilon ^{-1}}$.
Now we prove the equivalence between the three statements. The equivalence (i) ![]() $\Leftrightarrow$ (ii) is proved as above by replacing
$\Leftrightarrow$ (ii) is proved as above by replacing ![]() $K/Z_1$ by
$K/Z_1$ by ![]() $\mathcal {O}_D^{\times }/Z_D^1$ and noting that
$\mathcal {O}_D^{\times }/Z_D^1$ and noting that ![]() $\dim _{\mathbb {Q}_p}\mathcal {O}_D^{\times }/Z_D^1 =3[F_v:\mathbb {Q}_p]$.
$\dim _{\mathbb {Q}_p}\mathcal {O}_D^{\times }/Z_D^1 =3[F_v:\mathbb {Q}_p]$.
We prove part (ii) implies part (iii). Since ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$ is regular, we may choose a regular system of parameters of
$R_{\infty }^{\psi \varepsilon ^{-1}}$ is regular, we may choose a regular system of parameters of ![]() $\mathfrak {m}_{\infty }$, say
$\mathfrak {m}_{\infty }$, say ![]() $\underline {s}$. Since
$\underline {s}$. Since ![]() $M_{\infty }$ is flat over
$M_{\infty }$ is flat over ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$, the Koszul complex
$R_{\infty }^{\psi \varepsilon ^{-1}}$, the Koszul complex ![]() $K_{\bullet }(\underline {s}, M_{\infty })$ gives a resolution of
$K_{\bullet }(\underline {s}, M_{\infty })$ gives a resolution of ![]() $\pi ^{B'}(\overline {r})^{\vee }=M_{\infty }/\mathfrak {m}_{\infty }$:
$\pi ^{B'}(\overline {r})^{\vee }=M_{\infty }/\mathfrak {m}_{\infty }$:
It follows from Lemma 7.3(ii) that ![]() $\check {\mathcal {S}}^0(K_i(\underline {s},M_{\infty }))=0$ for any
$\check {\mathcal {S}}^0(K_i(\underline {s},M_{\infty }))=0$ for any ![]() $i$, hence
$i$, hence ![]() $\check {\mathcal {S}}^0(\mathrm {Im}(d_i))=0$ as well. It is then easy to deduce that the sequence
$\check {\mathcal {S}}^0(\mathrm {Im}(d_i))=0$ as well. It is then easy to deduce that the sequence
is exact, where ![]() $Q:=\mathrm {Im}(d_1)=\operatorname {{\mathrm {Ker}}}(d_0)$. On the other hand, the functor
$Q:=\mathrm {Im}(d_1)=\operatorname {{\mathrm {Ker}}}(d_0)$. On the other hand, the functor ![]() $\check {\mathcal {S}}^1$ is
$\check {\mathcal {S}}^1$ is ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$-equivariant, so the complex
$R_{\infty }^{\psi \varepsilon ^{-1}}$-equivariant, so the complex ![]() $\check {\mathcal {S}}^1 (K_{\bullet }(\underline {s}, M_{\infty }))$ is isomorphic to
$\check {\mathcal {S}}^1 (K_{\bullet }(\underline {s}, M_{\infty }))$ is isomorphic to ![]() $K_{\bullet }(\underline {s},\check {\mathcal {S}}^1 ( M_{\infty }))$, the Koszul complex with respect to
$K_{\bullet }(\underline {s},\check {\mathcal {S}}^1 ( M_{\infty }))$, the Koszul complex with respect to ![]() $\underline {s}$ and
$\underline {s}$ and ![]() $\check {\mathcal {S}}^1 (M_{\infty })$. Since
$\check {\mathcal {S}}^1 (M_{\infty })$. Since ![]() $\check {\mathcal {S}}^1 (M_{\infty })\cong N_{\infty }$ is flat over
$\check {\mathcal {S}}^1 (M_{\infty })\cong N_{\infty }$ is flat over ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$ by part (ii), the complex
$R_{\infty }^{\psi \varepsilon ^{-1}}$ by part (ii), the complex ![]() $\check {\mathcal {S}}^1 (K_{\bullet }(\underline {s}, M_{\infty }))$ is again exact. Together with (7.1) this implies that the map
$\check {\mathcal {S}}^1 (K_{\bullet }(\underline {s}, M_{\infty }))$ is again exact. Together with (7.1) this implies that the map
is injective.
The short exact sequence ![]() $0\to Q \to K_0(\underline {s}, M_{\infty }) {\buildrel {d_0} \over \longrightarrow} M_{\infty }/\mathfrak {m}_{\infty }\to 0$ induces an exact sequence
$0\to Q \to K_0(\underline {s}, M_{\infty }) {\buildrel {d_0} \over \longrightarrow} M_{\infty }/\mathfrak {m}_{\infty }\to 0$ induces an exact sequence
in which the first morphism is surjective by the injectivity of (7.2). Since ![]() $M_{\infty }^{\vee }|_{K}$ is injective in
$M_{\infty }^{\vee }|_{K}$ is injective in ![]() $\operatorname {\mathrm {Mod}}^{\rm sm}_{K,\psi }(\mathcal {O})$, Theorem 7.1(iii) implies
$\operatorname {\mathrm {Mod}}^{\rm sm}_{K,\psi }(\mathcal {O})$, Theorem 7.1(iii) implies ![]() $\check {\mathcal {S}}^2( K_0(\underline {s} , M_{\infty }) )=0$, thus
$\check {\mathcal {S}}^2( K_0(\underline {s} , M_{\infty }) )=0$, thus ![]() $\check {\mathcal {S}}^2 (M_{\infty }/\mathfrak {m}_{\infty }) = 0$ as required.
$\check {\mathcal {S}}^2 (M_{\infty }/\mathfrak {m}_{\infty }) = 0$ as required.
We prove part (iii) implies part (ii). This essentially follows from the above argument. Indeed, we deduce from part (iii) the injectivity of (7.2), which together with (7.1) implies the exactness of
In other words, the Koszul complex ![]() $\check {\mathcal {S}}^1 (K_{\bullet }(\underline {s}, M_{\infty }))$ is exact at degree
$\check {\mathcal {S}}^1 (K_{\bullet }(\underline {s}, M_{\infty }))$ is exact at degree ![]() $1$, thus
$1$, thus ![]() $\underline {s}$ is
$\underline {s}$ is ![]() $N_{\infty }$-regular by a standard argument.
$N_{\infty }$-regular by a standard argument.
Remark 7.5 Under some (stronger) genericity condition on ![]() $\overline {r}|_{G_{F_v}}$, the assumption on
$\overline {r}|_{G_{F_v}}$, the assumption on ![]() $\dim _K(\pi ^{B'}(\overline {r}))$ of Proposition 7.4 is verified in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Reference Hu and WangHW22].
$\dim _K(\pi ^{B'}(\overline {r}))$ of Proposition 7.4 is verified in [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Reference Hu and WangHW22].
We recall the following important result of Scholze.
Proposition 7.6 There is a ![]() $G_{\mathbb {Q}_p}\times D^{\times }$-equivariant inclusion
$G_{\mathbb {Q}_p}\times D^{\times }$-equivariant inclusion
whose cokernel is annihilated by ![]() $(\mathcal {O}_{D}^{\times })_1$, where
$(\mathcal {O}_{D}^{\times })_1$, where ![]() $(\mathcal {O}_{D}^{\times })_1$ denotes the reduced norm
$(\mathcal {O}_{D}^{\times })_1$ denotes the reduced norm ![]() $1$ elements of
$1$ elements of ![]() $\mathcal {O}_D^{\times }$. As a consequence, the cokernel is finite-dimensional over
$\mathcal {O}_D^{\times }$. As a consequence, the cokernel is finite-dimensional over ![]() $\mathbb {F}$ and
$\mathbb {F}$ and ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi ^{B'}(\overline {r}))=\dim _{\mathcal {O}_D^{\times }}\pi ^B(\overline {r})$.
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi ^{B'}(\overline {r}))=\dim _{\mathcal {O}_D^{\times }}\pi ^B(\overline {r})$.
Proof. The first assertion is a restatement of [Reference ScholzeScho18, Proposition 7.7] and [Reference PaškūnasPaš22, Lemma 6.1]. The second assertion follows from the first (note that we have fixed the central character).
7.3 Local–global compatibility (à la Emerton)
In this subsection, we assume ![]() $F_v\cong \mathbb {Q}_p$. Assume
$F_v\cong \mathbb {Q}_p$. Assume ![]() $\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })= \mathbb {F}$ where
$\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })= \mathbb {F}$ where ![]() $\overline {\rho }=\overline {r}_v(1)$, and let
$\overline {\rho }=\overline {r}_v(1)$, and let ![]() $\pi (\overline {\rho })$ be the admissible smooth representation of
$\pi (\overline {\rho })$ be the admissible smooth representation of ![]() $G=\mathrm {GL}_2(\mathbb {Q}_p)$ attached to
$G=\mathrm {GL}_2(\mathbb {Q}_p)$ attached to ![]() $\overline {\rho }$ (cf. § 4.2).
$\overline {\rho }$ (cf. § 4.2).
Theorem 7.7 We have ![]() $\pi ^{B'}(\overline {r})\cong \pi (\overline {\rho })^{\oplus d}$ for some
$\pi ^{B'}(\overline {r})\cong \pi (\overline {\rho })^{\oplus d}$ for some ![]() $d\geq 1$.
$d\geq 1$.
Proof. If ![]() $\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$ for any character
$\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$ for any character ![]() $\chi$, the result is essentially a consequence of [Reference EmertonEme11] (which treats the case of
$\chi$, the result is essentially a consequence of [Reference EmertonEme11] (which treats the case of ![]() $\mathrm {GL}_{2/\mathbb {Q}}$). In the definite quaternion algebra setting, the proof is carried out in [Reference Dospinescu and Le BrasDLB17, Appendix]. Note that in [Reference Dospinescu and Le BrasDLB17] the quaternion algebra is assumed to be over
$\mathrm {GL}_{2/\mathbb {Q}}$). In the definite quaternion algebra setting, the proof is carried out in [Reference Dospinescu and Le BrasDLB17, Appendix]. Note that in [Reference Dospinescu and Le BrasDLB17] the quaternion algebra is assumed to be over ![]() $\mathbb {Q}$, but the argument goes through in our setting, under the assumption that
$\mathbb {Q}$, but the argument goes through in our setting, under the assumption that ![]() $F_v$ is isomorphic to
$F_v$ is isomorphic to ![]() $\mathbb {Q}_p$. Another assumption made in [Reference Dospinescu and Le BrasDLB17] is that
$\mathbb {Q}_p$. Another assumption made in [Reference Dospinescu and Le BrasDLB17] is that ![]() $\overline {\rho }$ is irreducible, but the only places where this assumption is needed are as follows.
$\overline {\rho }$ is irreducible, but the only places where this assumption is needed are as follows.
– Page 403, the proof of Lemma 13.6. In our case, the proof goes through if we replace the vector
 $v$ (in [Reference Dospinescu and Le BrasDLB17]) by a finite-dimensional subspace which generates
$v$ (in [Reference Dospinescu and Le BrasDLB17]) by a finite-dimensional subspace which generates  $\pi (\overline {\rho })$ over
$\pi (\overline {\rho })$ over  $G$ (compare the proof of [Reference EmertonEme11, Theorem 6.3.12]).
$G$ (compare the proof of [Reference EmertonEme11, Theorem 6.3.12]).– Page 404, the proof of Lemma 13.9. To ensure that
 $r(\mathfrak {p})|_{G_{\mathbb {Q}_p}}$ is absolutely irreducible for
$r(\mathfrak {p})|_{G_{\mathbb {Q}_p}}$ is absolutely irreducible for  $\mathfrak {p}$ in a suitable set
$\mathfrak {p}$ in a suitable set  $\mathcal {C}$ defined before Lemma 13.8. But this can be avoided by replacing
$\mathcal {C}$ defined before Lemma 13.8. But this can be avoided by replacing  $\mathcal {C}$ by the subset of ‘allowable’ points as in [Reference EmertonEme11, Definition 5.4.7].
$\mathcal {C}$ by the subset of ‘allowable’ points as in [Reference EmertonEme11, Definition 5.4.7].– Page 405, the proof of the injectivity of
This can be proved as in the proof of [Reference EmertonEme11, Theorem 6.4.16] for \[ \pi(\overline{\rho})\otimes \operatorname{{\mathrm{Hom}}}_{G}(\pi(\overline{\rho}),\widetilde{S}_{\sigma_p^v, \psi} (U^{v}, \mathbb{F})_{\mathfrak{m}_{\overline{r}}})\rightarrow\widetilde{S}_{\sigma_p^v, \psi} (U^{v} , \mathbb{F})_{\mathfrak{m}_{\overline{r}}}. \]
\[ \pi(\overline{\rho})\otimes \operatorname{{\mathrm{Hom}}}_{G}(\pi(\overline{\rho}),\widetilde{S}_{\sigma_p^v, \psi} (U^{v}, \mathbb{F})_{\mathfrak{m}_{\overline{r}}})\rightarrow\widetilde{S}_{\sigma_p^v, \psi} (U^{v} , \mathbb{F})_{\mathfrak{m}_{\overline{r}}}. \]
 $\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$.
$\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$.
If ![]() $\overline {\rho }\sim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$, the result follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, § 4]. We remark that a multiplicity one assumption is made in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, § 4], but the necessary modification is given in [Reference Gee and NewtonGN22, § 5].
$\overline {\rho }\sim \big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$, the result follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, § 4]. We remark that a multiplicity one assumption is made in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, § 4], but the necessary modification is given in [Reference Gee and NewtonGN22, § 5].
Remark 7.8 In fact, [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and ShinCEG+18, Theorem 4.32] and its generalization [Reference Gee and NewtonGN22, Corollary 5.3.2] prove a much stronger statement than Theorem 7.7. Namely, assuming moreover that ![]() $\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi \omega } & {*}\\ {0} & {\chi }\end{smallmatrix}\big )$ for any character
$\overline {\rho }\nsim \big (\begin{smallmatrix} {\chi \omega } & {*}\\ {0} & {\chi }\end{smallmatrix}\big )$ for any character ![]() $\chi$, there is an isomorphism in
$\chi$, there is an isomorphism in ![]() $\frak {C}_{G,\psi }(R_{\infty }^{\psi \varepsilon ^{-1}})$
$\frak {C}_{G,\psi }(R_{\infty }^{\psi \varepsilon ^{-1}})$
where ![]() $N:= N_{\psi }\in \frak {C}_{G,\psi }(\mathcal {O})$ is the object attached to
$N:= N_{\psi }\in \frak {C}_{G,\psi }(\mathcal {O})$ is the object attached to ![]() $\overline {\rho }$ in § 4.2.1, and
$\overline {\rho }$ in § 4.2.1, and ![]() $d$ is the integer in Theorem 7.7.
$d$ is the integer in Theorem 7.7.
Corollary 7.9 Maintain the global assumptions we have made in Theorem 6.11, and assume up to twist ![]() $\overline {\rho } \sim \big (\begin{smallmatrix} {\mathrm {unr}_1 \omega } & {*}\\ {0} & {\mathrm {unr}_2}\end{smallmatrix}\big )$. Then
$\overline {\rho } \sim \big (\begin{smallmatrix} {\mathrm {unr}_1 \omega } & {*}\\ {0} & {\mathrm {unr}_2}\end{smallmatrix}\big )$. Then ![]() $\dim _{\mathcal {O}_D^{\times }}(\pi ^B(\overline {r}))=1$.
$\dim _{\mathcal {O}_D^{\times }}(\pi ^B(\overline {r}))=1$.
Proof. As in the proof of Theorem 6.11, it suffices to prove ![]() $\dim _{\mathcal {O}_D^{\times }}(\pi ^B(\overline {r}))\leq 1$. We reduce the result to a situation covered by Theorem 6.11.
$\dim _{\mathcal {O}_D^{\times }}(\pi ^B(\overline {r}))\leq 1$. We reduce the result to a situation covered by Theorem 6.11.
Let ![]() $\overline {\rho }'\sim \big (\begin{smallmatrix} {\mathrm {unr}_2} & {*}\\ {0} & {\mathrm {unr}_1\omega }\end{smallmatrix}\big )$ with
$\overline {\rho }'\sim \big (\begin{smallmatrix} {\mathrm {unr}_2} & {*}\\ {0} & {\mathrm {unr}_1\omega }\end{smallmatrix}\big )$ with ![]() $*\neq 0$. Choose a global setup, namely a totally real field
$*\neq 0$. Choose a global setup, namely a totally real field ![]() $\widetilde {F}$, an indefinite quaternion algebra
$\widetilde {F}$, an indefinite quaternion algebra ![]() $\widetilde {B}$ over
$\widetilde {B}$ over ![]() $\widetilde {F}$ which is ramified at
$\widetilde {F}$ which is ramified at ![]() $v$, and a modular absolutely irreducible Galois representation
$v$, and a modular absolutely irreducible Galois representation ![]() $\overline {r}'$ as in Theorem 6.11, such that
$\overline {r}'$ as in Theorem 6.11, such that ![]() $\overline {\rho }'\cong \overline {r}_v'(1)$. Then
$\overline {\rho }'\cong \overline {r}_v'(1)$. Then ![]() $\overline {\rho }'$ satisfies (C2) in § 4.3, and so
$\overline {\rho }'$ satisfies (C2) in § 4.3, and so ![]() $\dim _{\mathcal {O}_D^{\times }}(\pi ^{\widetilde {B}}(\overline {r}'))=1$ by Theorem 6.11(ii). Combining Theorem 7.7 and Proposition 7.6, we deduce that
$\dim _{\mathcal {O}_D^{\times }}(\pi ^{\widetilde {B}}(\overline {r}'))=1$ by Theorem 6.11(ii). Combining Theorem 7.7 and Proposition 7.6, we deduce that ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi (\overline {\rho }'))\leq 1$. The structure of
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi (\overline {\rho }'))\leq 1$. The structure of ![]() $\pi (\overline {\rho }')$ is recalled in § 4.2. In particular, the set
$\pi (\overline {\rho }')$ is recalled in § 4.2. In particular, the set ![]() $\operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }'))$ consists of non-supersingular representations. Using Theorem 7.1(iv) and Ludwig's result [Reference LudwigLud17], we have
$\operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }'))$ consists of non-supersingular representations. Using Theorem 7.1(iv) and Ludwig's result [Reference LudwigLud17], we have
for any non-supersingular irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G$. We deduce that
$G$. We deduce that ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi )\leq 1$ for any
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi )\leq 1$ for any ![]() $\pi \in \operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }'))$. It is clear from the definition of
$\pi \in \operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }'))$. It is clear from the definition of ![]() $\pi (\overline {\rho })$ (see § 4.2 or Proposition 8.14) that
$\pi (\overline {\rho })$ (see § 4.2 or Proposition 8.14) that ![]() $\operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }))$ differs from
$\operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }))$ differs from ![]() $\operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }'))$ by at most one-dimensional representations. Hence, using (7.3) we obtain
$\operatorname {{\mathrm {JH}}}(\pi (\overline {\rho }'))$ by at most one-dimensional representations. Hence, using (7.3) we obtain
By Theorem 7.7 and Proposition 7.6 again, this implies ![]() $\dim _{\mathcal {O}_D^{\times }}(\pi ^B(\overline {r}))\leq 1$.
$\dim _{\mathcal {O}_D^{\times }}(\pi ^B(\overline {r}))\leq 1$.
7.4 Vanishing for supersingular representations
Ludwig [Reference LudwigLud17] has proved that ![]() $\mathcal {S}^2(\pi )=0$ if
$\mathcal {S}^2(\pi )=0$ if ![]() $\pi$ is a principal series of
$\pi$ is a principal series of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$. Together with Theorem 6.11, we deduce the following vanishing result when
$\mathrm {GL}_2(\mathbb {Q}_p)$. Together with Theorem 6.11, we deduce the following vanishing result when ![]() $\pi$ is supersingular.
$\pi$ is supersingular.
Corollary 7.10 Assume that ![]() $\pi = \pi (\overline {\rho })$ is supersingular with
$\pi = \pi (\overline {\rho })$ is supersingular with ![]() $2\leq r\leq p-3$ in the notation of (C1) in § 4.3. Then
$2\leq r\leq p-3$ in the notation of (C1) in § 4.3. Then ![]() $\mathcal {S}^2(\pi )=0$. Moreover, we have
$\mathcal {S}^2(\pi )=0$. Moreover, we have ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi )=1$.
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi )=1$.
Proof. As ![]() $\overline {\rho }$ is irreducible, the ring
$\overline {\rho }$ is irreducible, the ring ![]() $R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth. It is proved in [Reference PaškūnasPaš22, Lemma 5.16] that
$R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth. It is proved in [Reference PaškūnasPaš22, Lemma 5.16] that ![]() $\dim _{K}(\pi )=1$, so the assumptions of Proposition 7.4 hold via Theorem 7.7. The existence of a suitable
$\dim _{K}(\pi )=1$, so the assumptions of Proposition 7.4 hold via Theorem 7.7. The existence of a suitable ![]() $B'$ and
$B'$ and ![]() $\overline {r}$ is well-known; see, for example, [Reference Diamond and TaylorDT94]. Thus, the vanishing of
$\overline {r}$ is well-known; see, for example, [Reference Diamond and TaylorDT94]. Thus, the vanishing of ![]() $\mathcal {S}^2(\pi )$ follows from this and Proposition 7.4. Finally, Theorem 6.11 and Proposition 7.6 imply that
$\mathcal {S}^2(\pi )$ follows from this and Proposition 7.4. Finally, Theorem 6.11 and Proposition 7.6 imply that ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi ^{B'}(\overline {r}))=1$, hence also
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi ^{B'}(\overline {r}))=1$, hence also ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi )=1$ via Theorem 7.7 again.
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1(\pi )=1$ via Theorem 7.7 again.
8. Further studies on Scholze's functor
In this section, we study the behavior of ![]() $\mathcal {S}^i$ on some non-supersingular representations of
$\mathcal {S}^i$ on some non-supersingular representations of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$. Recall that
$\mathrm {GL}_2(\mathbb {Q}_p)$. Recall that ![]() $p\geq 5$.
$p\geq 5$.
8.1 Preparations
8.1.1 Some definitions
Recall that ![]() $D$ is the nonsplit quaternion algebra over
$D$ is the nonsplit quaternion algebra over ![]() $\mathbb {Q}_p$ and
$\mathbb {Q}_p$ and ![]() $U_D^1=1+\mathfrak {p}_D$.
$U_D^1=1+\mathfrak {p}_D$.
Definition 8.1 Given an admissible smooth ![]() $\mathbb {F}$-representation
$\mathbb {F}$-representation ![]() $V$ of
$V$ of ![]() $D^{\times }$, let
$D^{\times }$, let ![]() $V_{\rm fd}$ be the largest finite-dimensional quotient of
$V_{\rm fd}$ be the largest finite-dimensional quotient of ![]() $V$.
$V$.
Remark 8.2 That ![]() $V_{\rm fd}$ is well-defined can be seen as follows. Let
$V_{\rm fd}$ is well-defined can be seen as follows. Let ![]() $V^{\vee }$ be the Pontryagin dual of
$V^{\vee }$ be the Pontryagin dual of ![]() $V$. Then by the general theory of finitely generated modules over
$V$. Then by the general theory of finitely generated modules over ![]() $\mathbb {F}[\![U_D^1]\!]$ (see, e.g., [Reference VenjakobVen02, § 3.1]),
$\mathbb {F}[\![U_D^1]\!]$ (see, e.g., [Reference VenjakobVen02, § 3.1]), ![]() $V^{\vee }$ has a largest submodule of
$V^{\vee }$ has a largest submodule of ![]() $\delta$-dimension
$\delta$-dimension ![]() $0$ (i.e. finite dimensional over
$0$ (i.e. finite dimensional over ![]() $\mathbb {F}$). Clearly this submodule is
$\mathbb {F}$). Clearly this submodule is ![]() $D^{\times }$-stable because
$D^{\times }$-stable because ![]() $V^{\vee }$ carries a compatible action of
$V^{\vee }$ carries a compatible action of ![]() $D^{\times }$. Taking the dual back gives
$D^{\times }$. Taking the dual back gives ![]() $V_{\rm fd}$ in Definition 8.1.
$V_{\rm fd}$ in Definition 8.1.
We give some basic properties of ![]() $(\cdot )_{\rm fd}$. For
$(\cdot )_{\rm fd}$. For ![]() $i\geq 0$ and
$i\geq 0$ and ![]() $M$ a finitely generated
$M$ a finitely generated ![]() $\mathbb {F}[\![U_D^1]\!]$-module, set
$\mathbb {F}[\![U_D^1]\!]$-module, set
Note that ![]() $\mathrm {E}^i(-)=0$ for
$\mathrm {E}^i(-)=0$ for ![]() $i\geq 5$, as
$i\geq 5$, as ![]() $\mathbb {F}[\![U_D^1]\!]$ is an Auslander regular ring of global dimension
$\mathbb {F}[\![U_D^1]\!]$ is an Auslander regular ring of global dimension ![]() $4$. Also recall that
$4$. Also recall that ![]() $M$ (when it is nonzero) is called Cohen–Macaulay if there exists exactly one
$M$ (when it is nonzero) is called Cohen–Macaulay if there exists exactly one ![]() $i$ such that
$i$ such that ![]() $\mathrm {E}^i(M)\neq 0$; in this case
$\mathrm {E}^i(M)\neq 0$; in this case ![]() $i$ equals to the grade of
$i$ equals to the grade of ![]() $M$.
$M$.
Lemma 8.3 Let ![]() $V$ be an admissible smooth
$V$ be an admissible smooth ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $D^{\times }$. If
$D^{\times }$. If ![]() $V$ is infinite-dimensional (as an
$V$ is infinite-dimensional (as an ![]() $\mathbb {F}$-vector space) and
$\mathbb {F}$-vector space) and ![]() $V^{\vee }$ is Cohen–Macaulay as an
$V^{\vee }$ is Cohen–Macaulay as an ![]() $\mathbb {F}[\![U_D^1]\!]$-module, then
$\mathbb {F}[\![U_D^1]\!]$-module, then ![]() $V_{\rm fd}=0$.
$V_{\rm fd}=0$.
Proof. By assumption, ![]() $V^{\vee }$ is Cohen–Macaulay with
$V^{\vee }$ is Cohen–Macaulay with ![]() $\dim _{\mathcal {O}_D^{\times }}(V)\geq 1$, thus
$\dim _{\mathcal {O}_D^{\times }}(V)\geq 1$, thus ![]() $\mathrm {E}^4(V^{\vee }) = 0$. If
$\mathrm {E}^4(V^{\vee }) = 0$. If ![]() $V_{\rm fd}\neq 0$, then the inclusion
$V_{\rm fd}\neq 0$, then the inclusion ![]() $(V_{\rm fd})^{\vee }\hookrightarrow V^{\vee }$ induces a surjection
$(V_{\rm fd})^{\vee }\hookrightarrow V^{\vee }$ induces a surjection
This gives a contradiction as ![]() $\mathrm {E}^4((V_{\rm fd})^{\vee })\neq 0$.
$\mathrm {E}^4((V_{\rm fd})^{\vee })\neq 0$.
Lemma 8.4 If ![]() $0\rightarrow V'\rightarrow V\rightarrow V''\rightarrow 0$ is a short exact sequence of admissible smooth
$0\rightarrow V'\rightarrow V\rightarrow V''\rightarrow 0$ is a short exact sequence of admissible smooth ![]() $\mathbb {F}$-representations of
$\mathbb {F}$-representations of ![]() $D^{\times }$, then
$D^{\times }$, then ![]() $(V')_{\rm fd}\rightarrow V_{\rm fd}\rightarrow (V'')_{\rm fd}\rightarrow 0$ is exact. If, moreover,
$(V')_{\rm fd}\rightarrow V_{\rm fd}\rightarrow (V'')_{\rm fd}\rightarrow 0$ is exact. If, moreover, ![]() $V''$ is finite-dimensional over
$V''$ is finite-dimensional over ![]() $\mathbb {F}$, then
$\mathbb {F}$, then
is exact.
Proof. It is obvious from Definition 8.1.
Lemma 8.5 Let ![]() $V$ be an admissible smooth
$V$ be an admissible smooth ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $D^{\times }$. Assume that
$D^{\times }$. Assume that ![]() $V$ carries an
$V$ carries an ![]() $\mathbb {F}$-linear continuous action of
$\mathbb {F}$-linear continuous action of ![]() $G_{\mathbb {Q}_p}$ which commutes with the action of
$G_{\mathbb {Q}_p}$ which commutes with the action of ![]() $D^{\times }$. Then
$D^{\times }$. Then ![]() $V_{\rm fd}$ is also stable under
$V_{\rm fd}$ is also stable under ![]() $G_{\mathbb {Q}_p}$.
$G_{\mathbb {Q}_p}$.
Proof. Consider the Pontryagin dual ![]() $V^{\vee }$, so that
$V^{\vee }$, so that ![]() $(V_{\rm fd})^{\vee }$ is identified with the largest finite-dimensional submodule of
$(V_{\rm fd})^{\vee }$ is identified with the largest finite-dimensional submodule of ![]() $V^{\vee }$, see Remark 8.2. It suffices to prove the following statement: if
$V^{\vee }$, see Remark 8.2. It suffices to prove the following statement: if ![]() $x\in V^{\vee }$ such that
$x\in V^{\vee }$ such that ![]() $\langle D^{\times }. x\rangle$ is finite-dimensional, then so is
$\langle D^{\times }. x\rangle$ is finite-dimensional, then so is ![]() $\langle D^{\times }. (gx)\rangle$ for any
$\langle D^{\times }. (gx)\rangle$ for any ![]() $g\in G_{\mathbb {Q}_p}$. This is clear because the actions of
$g\in G_{\mathbb {Q}_p}$. This is clear because the actions of ![]() $G_{\mathbb {Q}_p}$ and of
$G_{\mathbb {Q}_p}$ and of ![]() $D^{\times }$ commute.
$D^{\times }$ commute.
We now recall the notion of being ![]() $\sigma$-typic from [Reference ScholzeScho18, Definition 5.2], adapted to our situation. Let
$\sigma$-typic from [Reference ScholzeScho18, Definition 5.2], adapted to our situation. Let ![]() $G$ be a group,
$G$ be a group, ![]() $\sigma :G\rightarrow \mathrm {GL}_n(\mathbb {F})$ be an
$\sigma :G\rightarrow \mathrm {GL}_n(\mathbb {F})$ be an ![]() $n$-dimensional representation and
$n$-dimensional representation and ![]() $M$ an
$M$ an ![]() $\mathbb {F}[G]$-module. Then
$\mathbb {F}[G]$-module. Then ![]() $M$ is said to be
$M$ is said to be ![]() $\sigma$-typic if one can write
$\sigma$-typic if one can write ![]() $M$ as a tensor product
$M$ as a tensor product
such that ![]() $G$ acts on
$G$ acts on ![]() $\sigma \otimes _{\mathbb {F}}M_0$ through its action on
$\sigma \otimes _{\mathbb {F}}M_0$ through its action on ![]() $\sigma$.
$\sigma$.
Lemma 8.6 Assume that ![]() $\operatorname {{\mathrm {End}}}_{\mathbb {F}[G]}(\sigma )=\mathbb {F}$.
$\operatorname {{\mathrm {End}}}_{\mathbb {F}[G]}(\sigma )=\mathbb {F}$.
(i) If
 $M$ is
$M$ is  $\sigma$-typic, then
$\sigma$-typic, then  $M_0\cong \operatorname {{\mathrm {Hom}}}_{\mathbb {F}[G]}(\sigma,M)$.
$M_0\cong \operatorname {{\mathrm {Hom}}}_{\mathbb {F}[G]}(\sigma,M)$.(ii) Let
 $M'\subset M$ be
$M'\subset M$ be  $\mathbb {F}[G]$-modules and assume that
$\mathbb {F}[G]$-modules and assume that  $M'$ is a direct summand of
$M'$ is a direct summand of  $M$. If
$M$. If  $M$ is
$M$ is  $\sigma$-typic, then so is
$\sigma$-typic, then so is  $M'$.
$M'$.
Proof. (i) This follows from the same proof of [Reference ScholzeScho18, Proposition 5.3]. In [Reference ScholzeScho18, Proposition 5.3] ![]() $\sigma$ is assumed to be absolutely irreducible, but in the proof only the assumption
$\sigma$ is assumed to be absolutely irreducible, but in the proof only the assumption ![]() $\operatorname {{\mathrm {End}}}_{\mathbb {F}[G]}(\sigma )=\mathbb {F}$ is needed.
$\operatorname {{\mathrm {End}}}_{\mathbb {F}[G]}(\sigma )=\mathbb {F}$ is needed.
(ii) Since ![]() $M$ is
$M$ is ![]() $\sigma$-typic by assumption, the natural map
$\sigma$-typic by assumption, the natural map ![]() $\sigma \otimes \operatorname {{\mathrm {Hom}}}_{\mathbb {F}[G]}(\sigma,M)\rightarrow M$ is an isomorphism. Since
$\sigma \otimes \operatorname {{\mathrm {Hom}}}_{\mathbb {F}[G]}(\sigma,M)\rightarrow M$ is an isomorphism. Since ![]() $M'$ is a direct summand of
$M'$ is a direct summand of ![]() $M$, the map
$M$, the map
is also an isomorphism by functoriality.
8.1.2 Complements on Scholze's functor
Keep the notation from § 7 and assume ![]() $F_v\cong \mathbb {Q}_p$. To simplify notation we write
$F_v\cong \mathbb {Q}_p$. To simplify notation we write
It is a consequence of [Reference ScholzeScho18, Proposition 5.8] that ![]() $\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$ is
$\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$ is ![]() $\overline {r}$-typic, so
$\overline {r}$-typic, so
It is proved in [Reference ScholzeScho18, Proposition 7.7] and [Reference PaškūnasPaš22, Lemma 6.1] that there is a ![]() $G_{\mathbb {Q}_p}\times D^{\times }$-equivariant inclusion
$G_{\mathbb {Q}_p}\times D^{\times }$-equivariant inclusion
whose cokernel is finite-dimensional over ![]() $\mathbb {F}$, cf. Proposition 7.6.
$\mathbb {F}$, cf. Proposition 7.6.
Corollary 8.7 If ![]() $(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])^{\vee }$ is a Cohen–Macaulay
$(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])^{\vee }$ is a Cohen–Macaulay ![]() $\mathbb {F}[\![U_D^{1}]\!]$-module, then (8.2) becomes an equality.
$\mathbb {F}[\![U_D^{1}]\!]$-module, then (8.2) becomes an equality.
Proof. Since ![]() $\widetilde {H}^1 (U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$ is always infinite-dimensional, see [Reference Breuil and DiamondBD14, Corollary 3.2.4] or [Reference ScholzeScho18, Theorem 7.8], the assumption implies that
$\widetilde {H}^1 (U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$ is always infinite-dimensional, see [Reference Breuil and DiamondBD14, Corollary 3.2.4] or [Reference ScholzeScho18, Theorem 7.8], the assumption implies that ![]() $(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])_{\rm fd}=0$ by Lemma 8.3. The result follows.
$(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])_{\rm fd}=0$ by Lemma 8.3. The result follows.
Remark 8.8 Paškūnas [Reference PaškūnasPaš22, Lemma 6.1] also proves a criterion for (8.2) to be an equality. Corollary 8.7 can be viewed as a complement to it.
Proposition 8.9 Assume that ![]() $R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth and
$R_{v}^{\psi \varepsilon ^{-1}}$ is formally smooth and
Then ![]() $(\widetilde {H}^1(U^{v}, \mathcal {O})_{\mathfrak {m}_{\overline {r}}})^{d}$ is a faithfully flat
$(\widetilde {H}^1(U^{v}, \mathcal {O})_{\mathfrak {m}_{\overline {r}}})^{d}$ is a faithfully flat ![]() $\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$-module, and
$\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$-module, and ![]() $(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])^{\vee }$ is a Cohen–Macaulay
$(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])^{\vee }$ is a Cohen–Macaulay ![]() $\mathbb {F}[\![U_D^{1}]\!]$-module. In particular, (8.2) becomes an equality. Moreover,
$\mathbb {F}[\![U_D^{1}]\!]$-module. In particular, (8.2) becomes an equality. Moreover,
Proof. The faithful flatness is proved by the same argument of [Reference Gee and NewtonGN22, Theorem B(3)].
Since ![]() $N_{\infty }$ is a projective object in
$N_{\infty }$ is a projective object in ![]() $\frak {C}_{\mathcal {O}_{D}^{\times },\psi }(S_{\infty })$, it is a Cohen–Macaulay
$\frak {C}_{\mathcal {O}_{D}^{\times },\psi }(S_{\infty })$, it is a Cohen–Macaulay ![]() $S_{\infty }[\![U_D^1]\!]$-module, thus is also Cohen–Macaulay over
$S_{\infty }[\![U_D^1]\!]$-module, thus is also Cohen–Macaulay over ![]() $R_{\infty }[\![U_D^1]\!]$ by [Reference Gee and NewtonGN22, Lemma A.29]. The formal smoothness of
$R_{\infty }[\![U_D^1]\!]$ by [Reference Gee and NewtonGN22, Lemma A.29]. The formal smoothness of ![]() $R_{v}^{\psi \varepsilon ^{-1}}$ ensures that
$R_{v}^{\psi \varepsilon ^{-1}}$ ensures that ![]() $R_{\infty }$ is formally smooth, namely its maximal ideal
$R_{\infty }$ is formally smooth, namely its maximal ideal ![]() $\mathfrak {m}_{\infty }$ is generated by a regular sequence. By the proof of [Reference Gee and NewtonGN22, Proposition A.30],
$\mathfrak {m}_{\infty }$ is generated by a regular sequence. By the proof of [Reference Gee and NewtonGN22, Proposition A.30], ![]() $(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])^{\vee }\cong N_{\infty }/\mathfrak {m}_{\infty }$ is a Cohen–Macaulay
$(\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])^{\vee }\cong N_{\infty }/\mathfrak {m}_{\infty }$ is a Cohen–Macaulay ![]() $\mathbb {F}[\![U_D^1]\!]$-module.
$\mathbb {F}[\![U_D^1]\!]$-module.
The last assertion follows from Proposition 7.4.
For simplicity and clarity we make the following assumption in §§ 8.2 and 8.3 below. The general case will be treated in § 8.4.
(H) Assume ![]() $d=1$ in Theorem 7.7, i.e.
$d=1$ in Theorem 7.7, i.e. ![]() $\widetilde {S}(U^v,\mathbb {F})[\mathfrak {m}_{\overline {r}}]\cong \pi (\overline {\rho })$.
$\widetilde {S}(U^v,\mathbb {F})[\mathfrak {m}_{\overline {r}}]\cong \pi (\overline {\rho })$.
For notational convenience, we make the following definition. Let ![]() $\overline {\rho } : = \overline {r}_v(1)$.
$\overline {\rho } : = \overline {r}_v(1)$.
Definition 8.10 We define
which is an admissible smooth ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $D^{\times }$. Then (8.1) restricts to a
$D^{\times }$. Then (8.1) restricts to a ![]() $G_{\mathbb {Q}_p}\times D^{\times }$-isomorphism
$G_{\mathbb {Q}_p}\times D^{\times }$-isomorphism
Finally we recall the following important results which will be repeatedly used later on.
Theorem 8.11 Let ![]() $\pi$ be an admissible smooth
$\pi$ be an admissible smooth ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $G$.
$G$.
(i) The natural morphism
 $\mathcal {S}^0(\pi ^{\mathrm {SL}_2(\mathbb {Q}_p)})\rightarrow \mathcal {S}^0(\pi )$ is an isomorphism.
$\mathcal {S}^0(\pi ^{\mathrm {SL}_2(\mathbb {Q}_p)})\rightarrow \mathcal {S}^0(\pi )$ is an isomorphism.(ii) If
 $\pi \cong \operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^G\chi$ is a principal series (for some smooth character
$\pi \cong \operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^G\chi$ is a principal series (for some smooth character  $\chi :B(\mathbb {Q}_p)\rightarrow \mathbb {F}^{\times }$), then
$\chi :B(\mathbb {Q}_p)\rightarrow \mathbb {F}^{\times }$), then  $\mathcal {S}^2(\pi )=0$.
$\mathcal {S}^2(\pi )=0$.
Proof. Part (i) is a special case of Theorem 7.1(iv) and part (ii) is [Reference LudwigLud17, Theorem 4.6].
8.2 The generic case in the minimal case
In this subsection, we assume ![]() $\overline {\rho } \sim \big (\begin{smallmatrix} {\chi _1} & {*}\\ {0} & {\chi _2}\end{smallmatrix}\big )$ is reducible nonsplit such that
$\overline {\rho } \sim \big (\begin{smallmatrix} {\chi _1} & {*}\\ {0} & {\chi _2}\end{smallmatrix}\big )$ is reducible nonsplit such that ![]() $\chi _1 \chi _2^{-1} \neq \mathbf {1},~\omega ^{\pm 1}$.
$\chi _1 \chi _2^{-1} \neq \mathbf {1},~\omega ^{\pm 1}$.
Theorem 8.12 Let ![]() $\overline {\rho }$ be as above. Then
$\overline {\rho }$ be as above. Then ![]() $\mathrm {JL}(\overline {\rho })$ depends only on
$\mathrm {JL}(\overline {\rho })$ depends only on ![]() $\overline {\rho }^{\rm ss}$.
$\overline {\rho }^{\rm ss}$.
Proof. Write ![]() $\overline {\rho }_1$ (respectively,
$\overline {\rho }_1$ (respectively, ![]() $\overline {\rho }_2$) for the nonsplit extension
$\overline {\rho }_2$) for the nonsplit extension ![]() $\big (\begin{smallmatrix} {\chi _1} & {*}\\ {0} & {\chi _2}\end{smallmatrix}\big )$ (respectively,
$\big (\begin{smallmatrix} {\chi _1} & {*}\\ {0} & {\chi _2}\end{smallmatrix}\big )$ (respectively, ![]() $\big (\begin{smallmatrix} {\chi _2} & {*}\\ {0} & {\chi _1}\end{smallmatrix}\big )$). Combining Theorem 7.7 and [Reference PaškūnasPaš22, Proposition 6.7],Footnote 8 we see that
$\big (\begin{smallmatrix} {\chi _2} & {*}\\ {0} & {\chi _1}\end{smallmatrix}\big )$). Combining Theorem 7.7 and [Reference PaškūnasPaš22, Proposition 6.7],Footnote 8 we see that ![]() $\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1 (\widetilde {S}(U^v,\mathbb {F})[\mathfrak {m}_{\overline {r}}])=1$, hence
$\dim _{\mathcal {O}_D^{\times }}\mathcal {S}^1 (\widetilde {S}(U^v,\mathbb {F})[\mathfrak {m}_{\overline {r}}])=1$, hence
by (8.2). By Proposition 8.9, (8.4) and assumption (H), we obtain for ![]() $i\in \{0,1,2\}$
$i\in \{0,1,2\}$
Recall from § 4.2 that there exist exact sequences
where ![]() $\pi _1:=\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^G\chi _2\otimes \chi _1\omega ^{-1}$ and
$\pi _1:=\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^G\chi _2\otimes \chi _1\omega ^{-1}$ and ![]() $\pi _2:=\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^G\chi _1\otimes \chi _2\omega ^{-1}$. Note that
$\pi _2:=\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^G\chi _1\otimes \chi _2\omega ^{-1}$. Note that ![]() $\mathcal {S}^0(\pi _i)=\mathcal {S}^2(\pi _i)=0$ for
$\mathcal {S}^0(\pi _i)=\mathcal {S}^2(\pi _i)=0$ for ![]() $i\in \{1,2\}$, by Theorem 8.11. Hence, by applying the functor
$i\in \{1,2\}$, by Theorem 8.11. Hence, by applying the functor ![]() $\mathcal {S}^i$ and using (8.5), we obtain
$\mathcal {S}^i$ and using (8.5), we obtain
Since ![]() $\overline {\rho }_1$ is nonsplit, we have
$\overline {\rho }_1$ is nonsplit, we have
As a consequence, ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _2\omega ^{-1},\mathcal {S}^1(\pi _1))=0$ by (8.6) and applying
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _2\omega ^{-1},\mathcal {S}^1(\pi _1))=0$ by (8.6) and applying ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _2\omega ^{-1},-)$ to (8.7) gives isomorphisms
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _2\omega ^{-1},-)$ to (8.7) gives isomorphisms
where the last isomorphism follows from the definition of ![]() $\overline {\rho }_2$. This gives a
$\overline {\rho }_2$. This gives a ![]() $G_{\mathbb {Q}_p}\otimes D^{\times }$-equivariant embedding
$G_{\mathbb {Q}_p}\otimes D^{\times }$-equivariant embedding
One checks that its composition with ![]() $\iota _2$ (in (8.7)) coincides with the morphism obtained by tensoring the inclusion
$\iota _2$ (in (8.7)) coincides with the morphism obtained by tensoring the inclusion ![]() $\chi _2\omega ^{-1}\hookrightarrow \overline {\rho }_2(-1)$ with
$\chi _2\omega ^{-1}\hookrightarrow \overline {\rho }_2(-1)$ with ![]() $\mathrm {JL}(\overline {\rho }_2)$. Combining with the short exact sequence
$\mathrm {JL}(\overline {\rho }_2)$. Combining with the short exact sequence
a diagram chasing gives a surjection
In particular, when restricted to ![]() $G_{\mathbb {Q}_p}$,
$G_{\mathbb {Q}_p}$, ![]() $\mathcal {S}^1(\pi _1)$ is semisimple and any irreducible subquotient of
$\mathcal {S}^1(\pi _1)$ is semisimple and any irreducible subquotient of ![]() $\mathcal {S}^1(\pi _1)$ is isomorphic to
$\mathcal {S}^1(\pi _1)$ is isomorphic to ![]() $\chi _1\omega ^{-1}$.
$\chi _1\omega ^{-1}$.
On the other hand, the same argument as above implies an embedding (analogous to (8.8))
We claim that (8.10) is an isomorphism. Indeed, ![]() $\iota _1$ in (8.6) induces a
$\iota _1$ in (8.6) induces a ![]() $G_{\mathbb {Q}_p}\times D^{\times }$-equivariant embedding
$G_{\mathbb {Q}_p}\times D^{\times }$-equivariant embedding
However, as shown in the last paragraph, ![]() $\mathcal {S}^1(\pi _1)$ admits only
$\mathcal {S}^1(\pi _1)$ admits only ![]() $\chi _1\omega ^{-1}$ as irreducible subquotient (when restricted to
$\chi _1\omega ^{-1}$ as irreducible subquotient (when restricted to ![]() $G_{\mathbb {Q}_p}$), while
$G_{\mathbb {Q}_p}$), while ![]() $\chi _2\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_1)$ admits only
$\chi _2\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_1)$ admits only ![]() $\chi _2\omega ^{-1}$ as irreducible subquotients. Since
$\chi _2\omega ^{-1}$ as irreducible subquotients. Since ![]() $\chi _1\neq \chi _2$, this forces
$\chi _1\neq \chi _2$, this forces ![]() $\mathcal {S}^1(\pi _1)/(\chi _1\omega ^{-1}\otimes \mathrm {JL}( \overline {\rho }_1))=0$, proving the claim. In a similar way, the embedding (8.8) is also an isomorphism and consequently (8.9) is an isomorphism.
$\mathcal {S}^1(\pi _1)/(\chi _1\omega ^{-1}\otimes \mathrm {JL}( \overline {\rho }_1))=0$, proving the claim. In a similar way, the embedding (8.8) is also an isomorphism and consequently (8.9) is an isomorphism.
In summary, we have proven that
Hence, by applying ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1\omega ^{-1},-)$ we obtain a
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1\omega ^{-1},-)$ we obtain a ![]() $D^{\times }$-equivariant isomorphism
$D^{\times }$-equivariant isomorphism ![]() $\mathrm {JL}(\overline {\rho }_1)\cong \mathrm {JL}(\overline {\rho }_2)$.
$\mathrm {JL}(\overline {\rho }_1)\cong \mathrm {JL}(\overline {\rho }_2)$.
Remark 8.13 It might be strange that ![]() $\mathrm {JL}(\overline {\rho }_i)$ only carries the information of
$\mathrm {JL}(\overline {\rho }_i)$ only carries the information of ![]() $\overline {\rho }^{\rm ss}$. This can be explained as follows. On the one hand, since
$\overline {\rho }^{\rm ss}$. This can be explained as follows. On the one hand, since ![]() $\mathcal {S}^1(\pi (\overline {\rho }_i))=\overline {\rho }_i(-1)\otimes \mathrm {JL}(\overline {\rho }_i)$, the information of
$\mathcal {S}^1(\pi (\overline {\rho }_i))=\overline {\rho }_i(-1)\otimes \mathrm {JL}(\overline {\rho }_i)$, the information of ![]() $\overline {\rho }_i$ is indeed caught by the functor
$\overline {\rho }_i$ is indeed caught by the functor ![]() $\mathcal {S}^1$. On the other hand, comparing the quaternionic Serre weights (cf. Propositions 6.1 and 6.2),
$\mathcal {S}^1$. On the other hand, comparing the quaternionic Serre weights (cf. Propositions 6.1 and 6.2), ![]() $\mathrm {JL}(\overline {\rho }_1)$ and
$\mathrm {JL}(\overline {\rho }_1)$ and ![]() $\mathrm {JL}(\overline {\rho }_2)$ have the same set of quaternionic Serre weights. However, we do not expect this phenomenon happens once
$\mathrm {JL}(\overline {\rho }_2)$ have the same set of quaternionic Serre weights. However, we do not expect this phenomenon happens once ![]() $L\neq \mathbb {Q}_p$.
$L\neq \mathbb {Q}_p$.
8.3 The non-generic case in the minimal case
In this subsection, we extend the result in § 8.2 to the case ![]() $\overline {\rho }^{\rm ss}\sim \omega \oplus \mathbf {1}$ (up to twist). In the following, we will denote by
$\overline {\rho }^{\rm ss}\sim \omega \oplus \mathbf {1}$ (up to twist). In the following, we will denote by ![]() $\mathbf {1}_{G_{\mathbb {Q}_p}}$,
$\mathbf {1}_{G_{\mathbb {Q}_p}}$, ![]() $\mathbf {1}_{G}$ and
$\mathbf {1}_{G}$ and ![]() $\mathbf {1}_{D^{\times }}$ the trivial representation of
$\mathbf {1}_{D^{\times }}$ the trivial representation of ![]() $G_{\mathbb {Q}_p}$,
$G_{\mathbb {Q}_p}$, ![]() $G$ and
$G$ and ![]() $D^{\times }$, respectively; sometimes we will omit the subscript if no confusion is caused.
$D^{\times }$, respectively; sometimes we will omit the subscript if no confusion is caused.
Let ![]() $\overline {\rho }_1\sim \big (\begin{smallmatrix} {\omega } & {*}\\ {0} & {\mathbf {1}}\end{smallmatrix}\big )$ be a nonsplit extension of
$\overline {\rho }_1\sim \big (\begin{smallmatrix} {\omega } & {*}\\ {0} & {\mathbf {1}}\end{smallmatrix}\big )$ be a nonsplit extension of ![]() $\mathbf {1}$ by
$\mathbf {1}$ by ![]() $\omega$; we do not make assumptions on the extension type of
$\omega$; we do not make assumptions on the extension type of ![]() $\overline {\rho }_1$ (i.e. peu ramifié or très ramifié). On the other hand,
$\overline {\rho }_1$ (i.e. peu ramifié or très ramifié). On the other hand, ![]() $\operatorname {{\mathrm {Ext}}}^1_{G_{\mathbb {Q}_p}}(\omega,\mathbf {1})$ is one-dimensional; let
$\operatorname {{\mathrm {Ext}}}^1_{G_{\mathbb {Q}_p}}(\omega,\mathbf {1})$ is one-dimensional; let ![]() $\overline {\rho }_2\sim \big (\begin{smallmatrix} {\mathbf {1}} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$ be the unique nonsplit extension of
$\overline {\rho }_2\sim \big (\begin{smallmatrix} {\mathbf {1}} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$ be the unique nonsplit extension of ![]() $\omega$ by
$\omega$ by ![]() $\mathbf {1}$.
$\mathbf {1}$.
Let ![]() $\tau _1$ be the universal extension of
$\tau _1$ be the universal extension of ![]() $\mathbf{1}_{G}^{\oplus2}$ by
$\mathbf{1}_{G}^{\oplus2}$ by ![]() $\operatorname {{\mathrm {Sp}}}$, i.e.
$\operatorname {{\mathrm {Sp}}}$, i.e.
with ![]() $\operatorname {{\mathrm {soc}}}_{G}\tau _1=\operatorname {{\mathrm {Sp}}}$. Recall from § 4.2 that there is a short exact sequence
$\operatorname {{\mathrm {soc}}}_{G}\tau _1=\operatorname {{\mathrm {Sp}}}$. Recall from § 4.2 that there is a short exact sequence
where ![]() $\pi _{\alpha }:=\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^{G}(\omega \otimes \omega ^{-1})$.
$\pi _{\alpha }:=\operatorname {{\mathrm {Ind}}}_{B(\mathbb {Q}_p)}^{G}(\omega \otimes \omega ^{-1})$.
It is shown in [Reference PaškūnasPaš13, § 10.1] that ![]() $\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{G/Z_G}(\pi _{\alpha },\mathbf {1}_G)=1$. Thus, there exists a unique (up to isomorphism) nonsplit extension
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{G/Z_G}(\pi _{\alpha },\mathbf {1}_G)=1$. Thus, there exists a unique (up to isomorphism) nonsplit extension
On the other hand, there is a natural isomorphism ![]() $\operatorname {{\mathrm {Ext}}}^1_{G/Z_G}(\mathbf {1}_G,\operatorname {{\mathrm {Sp}}})\cong \operatorname {{\mathrm {Hom}}}(\mathbb {Q}_p^{\times },\mathbb {F})$ by [Reference ColmezCol10, Theorem VII.4.18]; we denote by
$\operatorname {{\mathrm {Ext}}}^1_{G/Z_G}(\mathbf {1}_G,\operatorname {{\mathrm {Sp}}})\cong \operatorname {{\mathrm {Hom}}}(\mathbb {Q}_p^{\times },\mathbb {F})$ by [Reference ColmezCol10, Theorem VII.4.18]; we denote by ![]() $E_{\phi }$ the extension corresponding to
$E_{\phi }$ the extension corresponding to ![]() $\phi \in \operatorname {{\mathrm {Hom}}}(\mathbb {Q}_p^{\times },\mathbb {F})$. The next result gives the structure of
$\phi \in \operatorname {{\mathrm {Hom}}}(\mathbb {Q}_p^{\times },\mathbb {F})$. The next result gives the structure of ![]() $\pi (\overline {\rho }_1)$.
$\pi (\overline {\rho }_1)$.
Proposition 8.14 We have ![]() $\operatorname {{\mathrm {soc}}}_G\pi (\overline {\rho }_1)\cong \operatorname {{\mathrm {Sp}}}$ and there exist nonsplit extensions
$\operatorname {{\mathrm {soc}}}_G\pi (\overline {\rho }_1)\cong \operatorname {{\mathrm {Sp}}}$ and there exist nonsplit extensions
Proof. See [Reference PaškūnasPaš15, Lemma 6.7].
Proposition 8.15 The following statements hold:
(i)
 $\mathcal {S}^0(\mathbf {1}_G)\cong \mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }}$,
$\mathcal {S}^0(\mathbf {1}_G)\cong \mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }}$,  $\mathcal {S}^1(\mathbf {1}_G)=0$,
$\mathcal {S}^1(\mathbf {1}_G)=0$,  $\mathcal {S}^2(\mathbf {1}_G)\cong \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$;
$\mathcal {S}^2(\mathbf {1}_G)\cong \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$;(ii)
 $\mathcal {S}^0(\operatorname {{\mathrm {Sp}}})=\mathcal {S}^2(\operatorname {{\mathrm {Sp}}})=0$;
$\mathcal {S}^0(\operatorname {{\mathrm {Sp}}})=\mathcal {S}^2(\operatorname {{\mathrm {Sp}}})=0$;(iii)
 $\mathcal {S}^0(\pi _{\alpha })=\mathcal {S}^2(\pi _{\alpha })=0$.
$\mathcal {S}^0(\pi _{\alpha })=\mathcal {S}^2(\pi _{\alpha })=0$.
Proof. Statement (i) follows from Theorem 7.1(v). Statements (ii) and (iii) are special cases of Theorem 8.11, except for ![]() $\mathcal {S}^2(\operatorname {{\mathrm {Sp}}})$ which is [Reference LudwigLud17, Corollary 4.7].
$\mathcal {S}^2(\operatorname {{\mathrm {Sp}}})$ which is [Reference LudwigLud17, Corollary 4.7].
Corollary 8.16 Let ![]() $\pi \in \operatorname {\mathrm {Mod}}_{G/Z}^{\rm l.adm}(\mathcal {O})$. Assume that each of the irreducible subquotients of
$\pi \in \operatorname {\mathrm {Mod}}_{G/Z}^{\rm l.adm}(\mathcal {O})$. Assume that each of the irreducible subquotients of ![]() $\pi$ lies in
$\pi$ lies in ![]() $\{\operatorname {{\mathrm {Sp}}},\mathbf {1}_G,\pi _{\alpha }\}$. Then
$\{\operatorname {{\mathrm {Sp}}},\mathbf {1}_G,\pi _{\alpha }\}$. Then ![]() $\mathcal {S}^0(\pi )$ (respectively,
$\mathcal {S}^0(\pi )$ (respectively, ![]() $\mathcal {S}^2(\pi )$) admits only
$\mathcal {S}^2(\pi )$) admits only ![]() $\mathbf {1}_{G_{\mathbb {Q}_p}}$ (respectively,
$\mathbf {1}_{G_{\mathbb {Q}_p}}$ (respectively, ![]() $\omega ^{-1}$) as subquotients when restricted to
$\omega ^{-1}$) as subquotients when restricted to ![]() $G_{\mathbb {Q}_p}$.
$G_{\mathbb {Q}_p}$.
Proof. This is a direct consequence of Proposition 8.15.
(i) We have that
 $\mathrm {JL}(\overline {\rho }_1)^{\vee }$ is a Cohen–Macaulay
$\mathrm {JL}(\overline {\rho }_1)^{\vee }$ is a Cohen–Macaulay  $\mathbb {F}[\![U_D^1]\!]$-module.
$\mathbb {F}[\![U_D^1]\!]$-module.(ii) We have
 $\mathcal {S}^1(\pi (\overline {\rho }_1))=\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)$ and
$\mathcal {S}^1(\pi (\overline {\rho }_1))=\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)$ and  $\mathcal {S}^2(\pi (\overline {\rho }_1))=0$.
$\mathcal {S}^2(\pi (\overline {\rho }_1))=0$.
Proof. Since ![]() $R_{\overline {\rho }_1}^{\psi \varepsilon }$ is formally smooth, the assertions follow from Corollary 7.9 and Proposition 8.9.
$R_{\overline {\rho }_1}^{\psi \varepsilon }$ is formally smooth, the assertions follow from Corollary 7.9 and Proposition 8.9.
Corollary 8.18 We have ![]() $\mathcal {S}^0(\kappa )\cong \mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }}$ and
$\mathcal {S}^0(\kappa )\cong \mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }}$ and ![]() $\mathcal {S}^2(\kappa )=0$.
$\mathcal {S}^2(\kappa )=0$.
Proof. Since ![]() $\mathcal {S}^0(\pi _{\alpha })=0$, the first assertion is a direct consequence of Proposition 8.15(i) via (8.12). Since
$\mathcal {S}^0(\pi _{\alpha })=0$, the first assertion is a direct consequence of Proposition 8.15(i) via (8.12). Since ![]() $\kappa$ is a quotient of
$\kappa$ is a quotient of ![]() $\pi (\overline {\rho }_1)$, the second assertion is a consequence of Proposition 8.17(ii).
$\pi (\overline {\rho }_1)$, the second assertion is a consequence of Proposition 8.17(ii).
By Propositions 8.15 and 8.17 and Corollary 8.18, the sequence ![]() $0\rightarrow \operatorname {{\mathrm {Sp}}}\rightarrow \pi (\overline {\rho }_1)\rightarrow \kappa \rightarrow 0$ (see Proposition 8.14) induces an exact sequence
$0\rightarrow \operatorname {{\mathrm {Sp}}}\rightarrow \pi (\overline {\rho }_1)\rightarrow \kappa \rightarrow 0$ (see Proposition 8.14) induces an exact sequence
Similarly, the sequence ![]() $0\rightarrow E_{\phi }\rightarrow \pi (\overline {\rho }_1)\rightarrow \pi _{\alpha }\rightarrow 0$ induces an exact sequence
$0\rightarrow E_{\phi }\rightarrow \pi (\overline {\rho }_1)\rightarrow \pi _{\alpha }\rightarrow 0$ induces an exact sequence
Lemma 8.19 We have ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\mathcal {S}^1(\operatorname {{\mathrm {Sp}}}))=0$, and
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\mathcal {S}^1(\operatorname {{\mathrm {Sp}}}))=0$, and ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\mathcal {S}^1(\tau _1))$ is finite-dimensional.
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\mathcal {S}^1(\tau _1))$ is finite-dimensional.
Proof. As ![]() $\overline {\rho }_1\sim \big (\begin{smallmatrix} {\omega } & {*}\\ {0} & {\mathbf {1}}\end{smallmatrix}\big )$ is assumed to be nonsplit, we have
$\overline {\rho }_1\sim \big (\begin{smallmatrix} {\omega } & {*}\\ {0} & {\mathbf {1}}\end{smallmatrix}\big )$ is assumed to be nonsplit, we have ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1))=0$, which implies the first assertion via (8.13). For the second assertion, we note that the short exact sequence
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1))=0$, which implies the first assertion via (8.13). For the second assertion, we note that the short exact sequence ![]() $0\rightarrow \operatorname {{\mathrm {Sp}}}\rightarrow \tau _1\rightarrow (\mathbf {1}_{G})^{\oplus 2}\rightarrow 0$ induces an exact sequence
$0\rightarrow \operatorname {{\mathrm {Sp}}}\rightarrow \tau _1\rightarrow (\mathbf {1}_{G})^{\oplus 2}\rightarrow 0$ induces an exact sequence
by Proposition 8.15(i). By applying ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},-)$ to (8.15), we obtain
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},-)$ to (8.15), we obtain
from which the result easily follows.
Proposition 8.20 There exists a short exact sequence
As a consequence, ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1}, \mathcal {S}^1(\pi (\overline {\rho }_2)))\cong \mathrm {JL}(\overline {\rho }_2)$.
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1}, \mathcal {S}^1(\pi (\overline {\rho }_2)))\cong \mathrm {JL}(\overline {\rho }_2)$.
Proof. We need to show that the cokernel of (8.2) is isomorphic to ![]() $(\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2}$. For this we need a refined version of [Reference ScholzeScho18, Proposition 7.7], which we put separately in Lemma 8.21 below. In our situation with
$(\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2}$. For this we need a refined version of [Reference ScholzeScho18, Proposition 7.7], which we put separately in Lemma 8.21 below. In our situation with ![]() $A=\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$,
$A=\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$, ![]() $I=\mathfrak {m}_{\overline {r}}$ and
$I=\mathfrak {m}_{\overline {r}}$ and ![]() $P:=(\widetilde {S}(U^{v}, \mathcal {O})_{\mathfrak {m}_{\overline {r}}})^{d}$, we are left to show
$P:=(\widetilde {S}(U^{v}, \mathcal {O})_{\mathfrak {m}_{\overline {r}}})^{d}$, we are left to show
by Proposition 8.15(i) (here we use [Reference PaškūnasPaš22, Proposition 5.4] to ensure that ![]() $P$ satisfies assumption (c) of Lemma 8.21). This is a consequence of [Reference HuHu21, Proposition 3.30], as we explain below. After enlarging
$P$ satisfies assumption (c) of Lemma 8.21). This is a consequence of [Reference HuHu21, Proposition 3.30], as we explain below. After enlarging ![]() $\mathbb {F}$, we may assume
$\mathbb {F}$, we may assume ![]() $\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}/\mathfrak {m}_{\overline {r}}\cong \mathbb {F}$.
$\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}/\mathfrak {m}_{\overline {r}}\cong \mathbb {F}$.
To be able to apply [Reference HuHu21, Proposition 3.30], we need to relate ![]() $P$ with
$P$ with ![]() $N$, where
$N$, where ![]() $N$ is the object introduced in § 4.2.1 for
$N$ is the object introduced in § 4.2.1 for ![]() $\overline {\rho }_2$. We do this by passing to
$\overline {\rho }_2$. We do this by passing to ![]() $M_{\infty }$. On the one hand, by Remark 7.8 and assumption (H) we have
$M_{\infty }$. On the one hand, by Remark 7.8 and assumption (H) we have ![]() $M_{\infty }\cong R_{\infty }^{\psi \varepsilon ^{-1}}\widehat {\otimes }_{R_{\overline {\rho }_2}^{\psi \varepsilon }}N$. Since
$M_{\infty }\cong R_{\infty }^{\psi \varepsilon ^{-1}}\widehat {\otimes }_{R_{\overline {\rho }_2}^{\psi \varepsilon }}N$. Since ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$ is flat over
$R_{\infty }^{\psi \varepsilon ^{-1}}$ is flat over ![]() $R_{\overline {\rho }_2}^{\psi \varepsilon }$, we deduce
$R_{\overline {\rho }_2}^{\psi \varepsilon }$, we deduce
On the other hand, ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$ acts on
$R_{\infty }^{\psi \varepsilon ^{-1}}$ acts on ![]() $P$ via the isomorphism (5.2)
$P$ via the isomorphism (5.2) ![]() $M_{\infty }/\frak {a}_{\infty }\cong P$, and the action factors through
$M_{\infty }/\frak {a}_{\infty }\cong P$, and the action factors through
Recall that ![]() $\frak {a}_{\infty }$ is generated by an
$\frak {a}_{\infty }$ is generated by an ![]() $M_{\infty }$-regular sequence
$M_{\infty }$-regular sequence ![]() $z_1,\ldots,z_q, y_1,\ldots,y_j$. By Proposition 4.21, this sequence is also
$z_1,\ldots,z_q, y_1,\ldots,y_j$. By Proposition 4.21, this sequence is also ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}$-regular and
$R_{\infty }^{\psi \varepsilon ^{-1}}$-regular and ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}/\mathfrak {a}_{\infty }$ acts faithfully on
$R_{\infty }^{\psi \varepsilon ^{-1}}/\mathfrak {a}_{\infty }$ acts faithfully on ![]() $P$. But
$P$. But ![]() $\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$ also acts faithfully on
$\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$ also acts faithfully on ![]() $P$, so the surjection
$P$, so the surjection ![]() $R_{\infty }^{\psi \varepsilon ^{-1}}/\mathfrak {a}_{\infty }\twoheadrightarrow \mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$ is actually an isomorphism.Footnote 9 Consequently,
$R_{\infty }^{\psi \varepsilon ^{-1}}/\mathfrak {a}_{\infty }\twoheadrightarrow \mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}}}$ is actually an isomorphism.Footnote 9 Consequently,
Combining this with (8.18), we deduce (8.17) from [Reference HuHu21, Proposition 3.30].
Lemma 8.21 Let ![]() $(A,\mathfrak {m})$ be a complete noetherian local
$(A,\mathfrak {m})$ be a complete noetherian local ![]() $\mathcal {O}$-algebra with
$\mathcal {O}$-algebra with ![]() $A/\mathfrak {m}\cong \mathbb {F}$ and
$A/\mathfrak {m}\cong \mathbb {F}$ and ![]() $P\in \frak {C}_{G/Z_G}(A)$. Assume that:
$P\in \frak {C}_{G/Z_G}(A)$. Assume that:
(a)
 $P$ is projective in the category of pseudo-compact
$P$ is projective in the category of pseudo-compact  $\mathcal {O}[\![K/Z_1]\!]$-modules;
$\mathcal {O}[\![K/Z_1]\!]$-modules;(b)
 $P_{\mathrm {SL}_2(\mathbb {Q}_p)}=0$;
$P_{\mathrm {SL}_2(\mathbb {Q}_p)}=0$;(c) each of the irreducible subquotients of
 $P^{\vee }$ lies in
$P^{\vee }$ lies in  $\{\operatorname {{\mathrm {Sp}}},\mathbf {1}_G,\pi _{\alpha }\}$.
$\{\operatorname {{\mathrm {Sp}}},\mathbf {1}_G,\pi _{\alpha }\}$.
Let ![]() $I$ be an ideal of
$I$ be an ideal of ![]() $A$. Then there exists an exact sequence
$A$. Then there exists an exact sequence
Proof. Choose a finite free resolution of ![]() $A/I$:
$A/I$: ![]() $\cdots \rightarrow F_1\rightarrow F_0\rightarrow A/I\rightarrow 0$. By applying
$\cdots \rightarrow F_1\rightarrow F_0\rightarrow A/I\rightarrow 0$. By applying ![]() $-\otimes _AP$ to it, we obtain a chain complex
$-\otimes _AP$ to it, we obtain a chain complex
whose homology computes ![]() $\operatorname {{\mathrm {Tor}}}_i^A(A/I,P)$. Since each
$\operatorname {{\mathrm {Tor}}}_i^A(A/I,P)$. Since each ![]() $F_i$ is a finite free
$F_i$ is a finite free ![]() $A$-module (for
$A$-module (for ![]() $i\geq 0$), assumption (a) implies that each
$i\geq 0$), assumption (a) implies that each ![]() $F_i\otimes _A P$ is projective when restricted to
$F_i\otimes _A P$ is projective when restricted to ![]() $K$, hence
$K$, hence ![]() $\check {\mathcal {S}}^2(F_i\otimes _A P)=0$ by Theorem 7.1(iii). Assumption (b) implies that
$\check {\mathcal {S}}^2(F_i\otimes _A P)=0$ by Theorem 7.1(iii). Assumption (b) implies that ![]() $\check {\mathcal {S}}^0(F_i\otimes _A P)=0$ by Theorem 7.1(iv). As a consequence,
$\check {\mathcal {S}}^0(F_i\otimes _A P)=0$ by Theorem 7.1(iv). As a consequence, ![]() $\check {\mathcal {S}}^0(\mathrm {Im}(d_i))=0$ for any
$\check {\mathcal {S}}^0(\mathrm {Im}(d_i))=0$ for any ![]() $i\geq 0$. On the other hand, since
$i\geq 0$. On the other hand, since ![]() $\check {\mathcal {S}}^3(-)=0$, we have
$\check {\mathcal {S}}^3(-)=0$, we have ![]() $\check {\mathcal {S}}^2(\mathrm {Im}(d_i))=0$ for
$\check {\mathcal {S}}^2(\mathrm {Im}(d_i))=0$ for ![]() $i\geq 1$.
$i\geq 1$.
We may split (part of) the complex (8.19) as
from which we deduce long exact sequences
 \begin{gather*} 0\rightarrow \check{\mathcal{S}}^2(A/I\otimes_A P)\rightarrow\check{\mathcal{S}}^1(\mathrm{Im}(d_1)) \overset{f}{\rightarrow}\check{\mathcal{S}}^1(F_0\otimes_AP)\rightarrow \check{\mathcal{S}}^1(A/I\otimes_A P)\rightarrow 0,\\ 0\rightarrow\check{\mathcal{S}}^1(\operatorname{{\mathrm{Ker}}}(d_1))\rightarrow\check{\mathcal{S}}^1(F_1\otimes_A P)\overset{g}{\rightarrow} \check{\mathcal{S}}^1(\mathrm{Im}(d_1))\rightarrow \check{\mathcal{S}}^0(\operatorname{{\mathrm{Ker}}}(d_1))\rightarrow0. \end{gather*}
\begin{gather*} 0\rightarrow \check{\mathcal{S}}^2(A/I\otimes_A P)\rightarrow\check{\mathcal{S}}^1(\mathrm{Im}(d_1)) \overset{f}{\rightarrow}\check{\mathcal{S}}^1(F_0\otimes_AP)\rightarrow \check{\mathcal{S}}^1(A/I\otimes_A P)\rightarrow 0,\\ 0\rightarrow\check{\mathcal{S}}^1(\operatorname{{\mathrm{Ker}}}(d_1))\rightarrow\check{\mathcal{S}}^1(F_1\otimes_A P)\overset{g}{\rightarrow} \check{\mathcal{S}}^1(\mathrm{Im}(d_1))\rightarrow \check{\mathcal{S}}^0(\operatorname{{\mathrm{Ker}}}(d_1))\rightarrow0. \end{gather*}
Note that ![]() $\check {\mathcal {S}}^1(F_i\otimes _A P)\cong F_i\otimes _A \check {\mathcal {S}}^1(P)$ (as
$\check {\mathcal {S}}^1(F_i\otimes _A P)\cong F_i\otimes _A \check {\mathcal {S}}^1(P)$ (as ![]() $F_i$ is a finite free
$F_i$ is a finite free ![]() $A$-module), and that there is an exact sequence
$A$-module), and that there is an exact sequence
by tensoring the sequence ![]() $F_1\rightarrow F_0\rightarrow A/I\rightarrow 0$ with
$F_1\rightarrow F_0\rightarrow A/I\rightarrow 0$ with ![]() $\check {\mathcal {S}}^1(P)$. Recall that a variant of the snake lemma shows that there is a long exact sequence
$\check {\mathcal {S}}^1(P)$. Recall that a variant of the snake lemma shows that there is a long exact sequence
In our situation, this gives (by considering the last four nonzero terms)
By Corollary 8.16, assumption (c) implies that ![]() $\partial$ is identically zero. Hence, we are left to show
$\partial$ is identically zero. Hence, we are left to show
which follows from the exact sequence ![]() $0\rightarrow \mathrm {Im}(d_2)\rightarrow \operatorname {{\mathrm {Ker}}}(d_1)\rightarrow \operatorname {{\mathrm {Tor}}}_1^A(A/I,P)\rightarrow 0$ (recall
$0\rightarrow \mathrm {Im}(d_2)\rightarrow \operatorname {{\mathrm {Ker}}}(d_1)\rightarrow \operatorname {{\mathrm {Tor}}}_1^A(A/I,P)\rightarrow 0$ (recall ![]() $\check {\mathcal {S}}^0(\mathrm {Im}(d_2))=0$ from the first paragraph of the proof).
$\check {\mathcal {S}}^0(\mathrm {Im}(d_2))=0$ from the first paragraph of the proof).
By Theorem 8.11 the short exact sequence ![]() $0\rightarrow \pi _{\alpha }\rightarrow \pi (\overline {\rho }_2)\rightarrow \tau _1\rightarrow 0$ induces an exact sequence
$0\rightarrow \pi _{\alpha }\rightarrow \pi (\overline {\rho }_2)\rightarrow \tau _1\rightarrow 0$ induces an exact sequence
Lemma 8.22 Both ![]() $\mathcal {S}^1(\pi _{\alpha })$ and
$\mathcal {S}^1(\pi _{\alpha })$ and ![]() $\mathcal {S}^1(\kappa )$ are
$\mathcal {S}^1(\kappa )$ are ![]() $\omega ^{-1}$-typic (when restricted to
$\omega ^{-1}$-typic (when restricted to ![]() $G_{\mathbb {Q}_p}$).
$G_{\mathbb {Q}_p}$).
Proof. We claim that ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\mathcal {S}^1(\pi _{\alpha }))=\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\mathcal {S}^1(\kappa ))=0$. Combining (8.20) with Proposition 8.20, we obtain an embedding
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\mathcal {S}^1(\pi _{\alpha }))=\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\mathcal {S}^1(\kappa ))=0$. Combining (8.20) with Proposition 8.20, we obtain an embedding
As ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\overline {\rho }_2(-1))=0$, we deduce that
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\overline {\rho }_2(-1))=0$, we deduce that ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\mathcal {S}^1(\pi _{\alpha }))=0$, as claimed. Using Proposition 8.15(i) and Corollary 8.18, the sequence
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathbf {1}_{G_{\mathbb {Q}_p}},\mathcal {S}^1(\pi _{\alpha }))=0$, as claimed. Using Proposition 8.15(i) and Corollary 8.18, the sequence ![]() $0\rightarrow \mathbf {1}_G\rightarrow \kappa \rightarrow \pi _{\alpha }\rightarrow 0$ induces an exact sequence
$0\rightarrow \mathbf {1}_G\rightarrow \kappa \rightarrow \pi _{\alpha }\rightarrow 0$ induces an exact sequence
which implies the claim for ![]() $\mathcal {S}^1(\kappa )$.
$\mathcal {S}^1(\kappa )$.
The claim implies that the surjection ![]() $\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)\twoheadrightarrow \mathcal {S}^1(\kappa )$ in (8.13) must factor as
$\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)\twoheadrightarrow \mathcal {S}^1(\kappa )$ in (8.13) must factor as
where the first quotient map is induced by the natural projection ![]() $\overline {\rho }_1(-1)\sim \big (\begin{smallmatrix} {\mathbf {1}} & {*}\\ {0} & {\omega ^{-1}}\end{smallmatrix}\big )\twoheadrightarrow \omega ^{-1}$. In particular,
$\overline {\rho }_1(-1)\sim \big (\begin{smallmatrix} {\mathbf {1}} & {*}\\ {0} & {\omega ^{-1}}\end{smallmatrix}\big )\twoheadrightarrow \omega ^{-1}$. In particular, ![]() $\mathcal {S}^1(\kappa )$ is
$\mathcal {S}^1(\kappa )$ is ![]() $\omega ^{-1}$-typic. Note that, being a subrepresentation of
$\omega ^{-1}$-typic. Note that, being a subrepresentation of ![]() $\overline {\rho }_2(-1)\otimes \mathrm {JL}(\overline {\rho }_2)$,
$\overline {\rho }_2(-1)\otimes \mathrm {JL}(\overline {\rho }_2)$, ![]() $\mathcal {S}^1(\pi _{\alpha })$ does not admit any
$\mathcal {S}^1(\pi _{\alpha })$ does not admit any ![]() $G_{\mathbb {Q}_p}$-subquotient isomorphic to a nontrivial self-extension of
$G_{\mathbb {Q}_p}$-subquotient isomorphic to a nontrivial self-extension of ![]() $\omega ^{-1}$, so
$\omega ^{-1}$, so ![]() $\mathcal {S}^1(\pi _{\alpha })$ is also
$\mathcal {S}^1(\pi _{\alpha })$ is also ![]() $\omega ^{-1}$-typic by (8.21).
$\omega ^{-1}$-typic by (8.21).
As a consequence of (8.16), there exists a ![]() $D^{\times }$-equivariant surjection
$D^{\times }$-equivariant surjection
We denote its kernel by ![]() $V_2$. Then
$V_2$. Then ![]() $\overline {\rho }_2(-1)\otimes \mathrm {JL}(\overline {\rho }_2)$ can be filtered by subrepresentations such that the graded pieces are isomorphic to
$\overline {\rho }_2(-1)\otimes \mathrm {JL}(\overline {\rho }_2)$ can be filtered by subrepresentations such that the graded pieces are isomorphic to
Using (8.16) again, we obtain the following short exact sequences:
Recall the definition of ![]() $V_{\rm fd}$ for an admissible smooth
$V_{\rm fd}$ for an admissible smooth ![]() $D^{\times }$-representation
$D^{\times }$-representation ![]() $V$ from Definition 8.1, and that taking
$V$ from Definition 8.1, and that taking ![]() $(-)_{\rm fd}$ is right exact by Lemma 8.4.
$(-)_{\rm fd}$ is right exact by Lemma 8.4.
Corollary 8.23 The following statements hold:
(i)
 $(\mathcal {S}^1(\kappa ))_{\rm fd}=0$ and
$(\mathcal {S}^1(\kappa ))_{\rm fd}=0$ and  $(\mathcal {S}^1(\pi _{\alpha }))_{\rm fd}\cong \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$;
$(\mathcal {S}^1(\pi _{\alpha }))_{\rm fd}\cong \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$;(ii)
 $(\mathcal {S}^1(E_{\phi }))_{\rm fd}$ is
$(\mathcal {S}^1(E_{\phi }))_{\rm fd}$ is  $\omega ^{-1}$-typic;
$\omega ^{-1}$-typic;(iii)
 $(\mathcal {S}^1(\tau _1))_{\rm fd}$ is
$(\mathcal {S}^1(\tau _1))_{\rm fd}$ is  $\omega ^{-1}$-typic;
$\omega ^{-1}$-typic;(iv)
 $(V_2)_{\rm fd}=0$.
$(V_2)_{\rm fd}=0$.
Proof. (i) Since ![]() $\mathcal {S}^1(\kappa )$ is a quotient of
$\mathcal {S}^1(\kappa )$ is a quotient of ![]() $\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)$ by (8.13) and
$\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)$ by (8.13) and ![]() $(\mathrm {JL}(\overline {\rho }_1))^{\vee }$ is Cohen–Macaulay by Proposition 8.17, we have
$(\mathrm {JL}(\overline {\rho }_1))^{\vee }$ is Cohen–Macaulay by Proposition 8.17, we have ![]() $\mathrm {JL}(\overline {\rho }_1)_{\rm fd}=0$ by Lemma 8.3, hence
$\mathrm {JL}(\overline {\rho }_1)_{\rm fd}=0$ by Lemma 8.3, hence ![]() $(\mathcal {S}^1(\kappa ))_{\rm fd}=0$ as well by the right exactness of
$(\mathcal {S}^1(\kappa ))_{\rm fd}=0$ as well by the right exactness of ![]() $(-)_{\rm fd}$. The second assertion follows from this, by applying Lemma 8.4 to (8.21).
$(-)_{\rm fd}$. The second assertion follows from this, by applying Lemma 8.4 to (8.21).
(ii) Recall the exact sequence (8.14)
Since ![]() $\mathcal {S}^1(\pi _{\alpha })$ is
$\mathcal {S}^1(\pi _{\alpha })$ is ![]() $\omega ^{-1}$-typic by Lemma 8.22, the morphism
$\omega ^{-1}$-typic by Lemma 8.22, the morphism ![]() $\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)\rightarrow \mathcal {S}^1(\pi _{\alpha })$ factors through the quotient
$\overline {\rho }_1(-1)\otimes \mathrm {JL}(\overline {\rho }_1)\rightarrow \mathcal {S}^1(\pi _{\alpha })$ factors through the quotient ![]() $\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_1)$. Let
$\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_1)$. Let ![]() $W$ be the admissible
$W$ be the admissible ![]() $\mathbb {F}$-representation of
$\mathbb {F}$-representation of ![]() $D^{\times }$ such that
$D^{\times }$ such that
Then one checks that ![]() $\mathcal {S}^1(E_{\phi })$ fits in the following exact sequence:
$\mathcal {S}^1(E_{\phi })$ fits in the following exact sequence:
Since ![]() $(\mathrm {JL}(\overline {\rho }_1))_{\rm fd}=0$ as seen in part (i), we deduce
$(\mathrm {JL}(\overline {\rho }_1))_{\rm fd}=0$ as seen in part (i), we deduce
In particular, ![]() $(\mathcal {S}^1(E_{\phi }))_{\rm fd}$ is
$(\mathcal {S}^1(E_{\phi }))_{\rm fd}$ is ![]() $\omega ^{-1}$-typic.
$\omega ^{-1}$-typic.
(iii) Note that there is a short exact sequence ![]() $0\rightarrow E_{\phi }\rightarrow \tau _1\rightarrow \mathbf {1}_{G}\rightarrow 0$ by the definition of
$0\rightarrow E_{\phi }\rightarrow \tau _1\rightarrow \mathbf {1}_{G}\rightarrow 0$ by the definition of ![]() $\tau _1$, see (8.11). By Proposition 8.15(i) it induces an exact sequence
$\tau _1$, see (8.11). By Proposition 8.15(i) it induces an exact sequence
The assertion then follows from part (ii) using Lemma 8.4.
(iv) We view ![]() $\mathcal {S}^1(\pi _{\alpha })$ as a subrepresentation of
$\mathcal {S}^1(\pi _{\alpha })$ as a subrepresentation of ![]() $\mathcal {S}^1(\pi (\overline {\rho }_2))$ via (8.20). Since
$\mathcal {S}^1(\pi (\overline {\rho }_2))$ via (8.20). Since ![]() $\mathcal {S}^1(\pi _{\alpha })$ is
$\mathcal {S}^1(\pi _{\alpha })$ is ![]() $\omega ^{-1}$-typic by Lemma 8.22, it is contained in
$\omega ^{-1}$-typic by Lemma 8.22, it is contained in ![]() $\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_2)$, see (8.23). As a consequence, the snake lemma applied to (8.20) and (8.23) implies that
$\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_2)$, see (8.23). As a consequence, the snake lemma applied to (8.20) and (8.23) implies that ![]() $\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes V_2$ is a quotient of
$\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes V_2$ is a quotient of ![]() $\mathcal {S}^1(\tau _1)$, thus
$\mathcal {S}^1(\tau _1)$, thus ![]() $(\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes V_2)_{\rm fd}$ is a quotient of
$(\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes V_2)_{\rm fd}$ is a quotient of ![]() $(\mathcal {S}^1(\tau _1))_{\rm fd}$. However,
$(\mathcal {S}^1(\tau _1))_{\rm fd}$. However, ![]() $(\mathcal {S}^1(\tau _1))_{\rm fd}$ is
$(\mathcal {S}^1(\tau _1))_{\rm fd}$ is ![]() $\omega ^{-1}$-typic by part (iii), which forces
$\omega ^{-1}$-typic by part (iii), which forces ![]() $(\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes V_2)_{\rm fd}=0$ or equivalently
$(\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes V_2)_{\rm fd}=0$ or equivalently ![]() $(V_2)_{\rm fd}=0$.
$(V_2)_{\rm fd}=0$.
Corollary 8.24 We have isomorphisms ![]() $\mathcal {S}^1(\kappa )\cong \omega ^{-1}\otimes V_2$ and
$\mathcal {S}^1(\kappa )\cong \omega ^{-1}\otimes V_2$ and
Proof. We may identify ![]() $\mathcal {S}^1(\kappa )$ with a subrepresentation of
$\mathcal {S}^1(\kappa )$ with a subrepresentation of ![]() $\mathcal {S}^1(\pi (\overline {\rho }_2))$ via (8.20) and (8.21). As in the proof of Corollary 8.23(iv),
$\mathcal {S}^1(\pi (\overline {\rho }_2))$ via (8.20) and (8.21). As in the proof of Corollary 8.23(iv), ![]() $\mathcal {S}^1(\kappa )$ is contained in
$\mathcal {S}^1(\kappa )$ is contained in ![]() $\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_2)$. However, since
$\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_2)$. However, since ![]() $(\mathcal {S}^1(\kappa ))_{\rm fd}=0$ by Corollary 8.23(i),
$(\mathcal {S}^1(\kappa ))_{\rm fd}=0$ by Corollary 8.23(i), ![]() $\mathcal {S}^1(\kappa )$ is, in fact, contained in
$\mathcal {S}^1(\kappa )$ is, in fact, contained in ![]() $\omega ^{-1}\otimes V_2$ by the definition of
$\omega ^{-1}\otimes V_2$ by the definition of ![]() $V_2$, see (8.22). Denote by
$V_2$, see (8.22). Denote by ![]() $\iota$ the inclusion
$\iota$ the inclusion
We need to prove that ![]() $\iota$ is an isomorphism or, equivalently,
$\iota$ is an isomorphism or, equivalently, ![]() $\operatorname {{\mathrm {Coker}}}(\iota )=0$. Since
$\operatorname {{\mathrm {Coker}}}(\iota )=0$. Since ![]() $(V_2)_{\rm fd}=0$ by Corollary 8.23(iv), it suffices to prove that
$(V_2)_{\rm fd}=0$ by Corollary 8.23(iv), it suffices to prove that ![]() $\operatorname {{\mathrm {Coker}}}(\iota )$ is finite-dimensional.
$\operatorname {{\mathrm {Coker}}}(\iota )$ is finite-dimensional.
Denote by ![]() $\widetilde {\iota }$ the embedding
$\widetilde {\iota }$ the embedding ![]() $\mathcal {S}^1(\kappa )\hookrightarrow \mathcal {S}^1(\pi (\overline {\rho }_2))$. Then (8.20) and (8.21) imply
$\mathcal {S}^1(\kappa )\hookrightarrow \mathcal {S}^1(\pi (\overline {\rho }_2))$. Then (8.20) and (8.21) imply
Since ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\mathcal {S}^1(\tau _1))$ is finite-dimensional by Lemma 8.19, so is
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\mathcal {S}^1(\tau _1))$ is finite-dimensional by Lemma 8.19, so is ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\operatorname {{\mathrm {Coker}}}(\widetilde {\iota }))$. On the other hand, using (8.24) we have a commutative diagram
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\operatorname {{\mathrm {Coker}}}(\widetilde {\iota }))$. On the other hand, using (8.24) we have a commutative diagram

hence an exact sequence
Consequently, ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\operatorname {{\mathrm {Coker}}}(\iota ))$ is finite-dimensional. However, since
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\omega ^{-1},\operatorname {{\mathrm {Coker}}}(\iota ))$ is finite-dimensional. However, since ![]() $\operatorname {{\mathrm {Coker}}}(\iota )$ is
$\operatorname {{\mathrm {Coker}}}(\iota )$ is ![]() $\omega ^{-1}$-typic (being a quotient of
$\omega ^{-1}$-typic (being a quotient of ![]() $\omega ^{-1}\otimes V_2$), this implies that
$\omega ^{-1}\otimes V_2$), this implies that ![]() $\operatorname {{\mathrm {Coker}}}(\iota )$ is itself finite-dimensional. As explained in last paragraph, we deduce that
$\operatorname {{\mathrm {Coker}}}(\iota )$ is itself finite-dimensional. As explained in last paragraph, we deduce that ![]() $\iota$ is an isomorphism and, consequently, by (8.28)
$\iota$ is an isomorphism and, consequently, by (8.28)
Finally, the second isomorphism in the corollary follows from this by using (8.27).
We note the following consequence of the proof of Corollary 8.24.
(i) There exists a short exact sequence of
 $G_{\mathbb {Q}_p}\times D^{\times }$-representations
$G_{\mathbb {Q}_p}\times D^{\times }$-representations
 \[ 0\rightarrow \omega^{-1}\otimes V_2\rightarrow \mathcal{S}^1(\pi_{\alpha})\rightarrow \omega^{-1}\otimes \mathbf{1}_{D^{\times}}\rightarrow0. \]
\[ 0\rightarrow \omega^{-1}\otimes V_2\rightarrow \mathcal{S}^1(\pi_{\alpha})\rightarrow \omega^{-1}\otimes \mathbf{1}_{D^{\times}}\rightarrow0. \]
(ii) There exists a
 $G_{\mathbb {Q}_p}\times D^{\times }$-equivariant surjection
$G_{\mathbb {Q}_p}\times D^{\times }$-equivariant surjection  $\mathcal {S}^1(\operatorname {{\mathrm {Sp}}})\twoheadrightarrow \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$ whose kernel admits only
$\mathcal {S}^1(\operatorname {{\mathrm {Sp}}})\twoheadrightarrow \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$ whose kernel admits only  $\mathbf {1}_{G_{\mathbb {Q}_p}}$ as subquotients when restricted to
$\mathbf {1}_{G_{\mathbb {Q}_p}}$ as subquotients when restricted to  $G_{\mathbb {Q}_p}$. In particular,
$G_{\mathbb {Q}_p}$. In particular,  $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathcal {S}^1(\operatorname {{\mathrm {Sp}}}),\omega ^{-1})$ is one-dimensional.
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathcal {S}^1(\operatorname {{\mathrm {Sp}}}),\omega ^{-1})$ is one-dimensional.
Recall from Propositions 6.1 and 6.2 that we always have ![]() $\mathbf {1}_{\mathcal {O}_D^{\times }}\in W_D(\overline {\rho }_1)$ (no matter
$\mathbf {1}_{\mathcal {O}_D^{\times }}\in W_D(\overline {\rho }_1)$ (no matter ![]() $\overline {\rho }_1$ is peu ramifié or très ramifié), so
$\overline {\rho }_1$ is peu ramifié or très ramifié), so
Let ![]() $W_1$ be the
$W_1$ be the ![]() $\mathbf {1}_{\mathcal {O}_D^{\times }}$-typic component of
$\mathbf {1}_{\mathcal {O}_D^{\times }}$-typic component of ![]() $\operatorname {{\mathrm {soc}}}_{\mathcal {O}_D^{\times }}\mathrm {JL}(\overline {\rho }_1)$. It is easy to see that
$\operatorname {{\mathrm {soc}}}_{\mathcal {O}_D^{\times }}\mathrm {JL}(\overline {\rho }_1)$. It is easy to see that ![]() $W_1$ is stable under
$W_1$ is stable under ![]() $D^{\times }$. Define
$D^{\times }$. Define ![]() $V_1$ to be the quotient
$V_1$ to be the quotient
The main result of this subsection is the following.
Theorem 8.26 There exists a ![]() $D^{\times }$-equivariant isomorphism
$D^{\times }$-equivariant isomorphism ![]() $V_1\cong V_2$.
$V_1\cong V_2$.
Proof. Recall the exact sequence (8.13)
By Corollary 8.25(ii), ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathcal {S}^1(\operatorname {{\mathrm {Sp}}}),\omega ^{-1})$ is one-dimensional over
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\mathcal {S}^1(\operatorname {{\mathrm {Sp}}}),\omega ^{-1})$ is one-dimensional over ![]() $\mathbb {F}$, so the last sequence shows that
$\mathbb {F}$, so the last sequence shows that ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\operatorname {{\mathrm {Ker}}}(j),\omega ^{-1})$ is also one-dimensional. Since
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\operatorname {{\mathrm {Ker}}}(j),\omega ^{-1})$ is also one-dimensional. Since ![]() $\mathcal {S}^1(\kappa )$ is
$\mathcal {S}^1(\kappa )$ is ![]() $\omega ^{-1}$-typic by Lemma 8.22, the surjection
$\omega ^{-1}$-typic by Lemma 8.22, the surjection ![]() $j$ factors as
$j$ factors as
We clearly have a short exact sequence
which implies that ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\operatorname {{\mathrm {Ker}}}(j'),\omega ^{-1})$ is also one-dimensional. Moreover, by Corollary 8.25(ii) again, it is easy to see that the one-dimensional
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\operatorname {{\mathrm {Ker}}}(j'),\omega ^{-1})$ is also one-dimensional. Moreover, by Corollary 8.25(ii) again, it is easy to see that the one-dimensional ![]() $\omega ^{-1}$-typic quotient of
$\omega ^{-1}$-typic quotient of ![]() $\operatorname {{\mathrm {Ker}}}(j')$ is isomorphic to
$\operatorname {{\mathrm {Ker}}}(j')$ is isomorphic to ![]() $\omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$. But
$\omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$. But ![]() $\operatorname {{\mathrm {Ker}}}(j')$ is itself
$\operatorname {{\mathrm {Ker}}}(j')$ is itself ![]() $\omega ^{-1}$-typic (being a subrepresentation of
$\omega ^{-1}$-typic (being a subrepresentation of ![]() $\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_1)$), so
$\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho }_1)$), so ![]() $\operatorname {{\mathrm {Ker}}}(j')$ is, in fact, isomorphic to
$\operatorname {{\mathrm {Ker}}}(j')$ is, in fact, isomorphic to ![]() $\omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$.
$\omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$.
On the other hand, since ![]() $\mathcal {S}^1(\kappa )\cong V_2$ as representations of
$\mathcal {S}^1(\kappa )\cong V_2$ as representations of ![]() $D^{\times }$ by Corollary 8.24, we have
$D^{\times }$ by Corollary 8.24, we have
for some integer ![]() $m_2\geq 1$, where the last isomorphism is given by Proposition 6.1, Proposition 6.2 and Corollary 6.8. Indeed, taking
$m_2\geq 1$, where the last isomorphism is given by Proposition 6.1, Proposition 6.2 and Corollary 6.8. Indeed, taking ![]() $r=p-3$ and
$r=p-3$ and ![]() $s=0$ in Proposition 6.1(ii)(c), we get
$s=0$ in Proposition 6.1(ii)(c), we get ![]() $W_D(\overline {\rho }_2)=\{\xi ^{p-3}\alpha ^{-1}\zeta,\xi ^{p(p-3)}\alpha \zeta \}=\{\alpha,\alpha ^{-1}\}$. We deduce that the composition
$W_D(\overline {\rho }_2)=\{\xi ^{p-3}\alpha ^{-1}\zeta,\xi ^{p(p-3)}\alpha \zeta \}=\{\alpha,\alpha ^{-1}\}$. We deduce that the composition
is zero, where the first morphism is induced from the natural inclusion ![]() $W_1\hookrightarrow \mathrm {JL}(\overline {\rho }_1)$, see (8.29). In other words,
$W_1\hookrightarrow \mathrm {JL}(\overline {\rho }_1)$, see (8.29). In other words, ![]() $\operatorname {{\mathrm {Ker}}}(j')$ contains
$\operatorname {{\mathrm {Ker}}}(j')$ contains ![]() $\omega ^{-1}\otimes W_1$. Combining with what has been proved in the last paragraph, this implies
$\omega ^{-1}\otimes W_1$. Combining with what has been proved in the last paragraph, this implies ![]() $\operatorname {{\mathrm {Ker}}}(j')=\omega ^{-1}\otimes W_1$. In particular,
$\operatorname {{\mathrm {Ker}}}(j')=\omega ^{-1}\otimes W_1$. In particular, ![]() $W_1\cong \mathbf {1}_{D^{\times }}$ and
$W_1\cong \mathbf {1}_{D^{\times }}$ and
Taking into account Corollary 8.24, we obtain
as representations of ![]() $D^{\times }$.
$D^{\times }$.
Lemma 8.27 Let ![]() $\chi :\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ be a smooth character.
$\chi :\mathcal {O}_D^{\times }\rightarrow \mathbb {F}^{\times }$ be a smooth character.
(i) If
 $\chi \notin W_D(\overline {\rho }_1)$, then
$\chi \notin W_D(\overline {\rho }_1)$, then  $\operatorname {{\mathrm {Ext}}}^i_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\mathrm {JL}(\overline {\rho }_1))=0$ for
$\operatorname {{\mathrm {Ext}}}^i_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\mathrm {JL}(\overline {\rho }_1))=0$ for  $i\geq 0$.
$i\geq 0$.(ii) If
 $\chi \notin W_D(\overline {\rho }_2)$, then
$\chi \notin W_D(\overline {\rho }_2)$, then  $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi,\mathrm {JL}(\overline {\rho }_2))=\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\mathrm {JL}(\overline {\rho }_2))=0$.
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi,\mathrm {JL}(\overline {\rho }_2))=\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\mathrm {JL}(\overline {\rho }_2))=0$.
Proof. (i) The proof is as in [Reference Hu and WangHW22, Proposition 10.10(i)]. The point is that ![]() $R_{\overline {\rho }_1}^{\psi \varepsilon }$ is formally smooth, so by Proposition 8.9
$R_{\overline {\rho }_1}^{\psi \varepsilon }$ is formally smooth, so by Proposition 8.9 ![]() $\widetilde {H}^1 (U^{v} , \mathcal {O})_{\mathfrak {m}_{\overline {r}_1}}^{d}$ is flat over
$\widetilde {H}^1 (U^{v} , \mathcal {O})_{\mathfrak {m}_{\overline {r}_1}}^{d}$ is flat over ![]() $\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}_1}}$ with fiber isomorphic to
$\mathbb {T}(U^v)_{\mathfrak {m}_{\overline {r}_1}}$ with fiber isomorphic to ![]() $\mathrm {JL}(\overline {\rho }_1)^{\vee }$. Here we write
$\mathrm {JL}(\overline {\rho }_1)^{\vee }$. Here we write ![]() $\overline {r}_1$ instead of
$\overline {r}_1$ instead of ![]() $\overline {r}$ to indicate that we are considering the case where
$\overline {r}$ to indicate that we are considering the case where ![]() $\overline {r}_v(1)=\overline {\rho }_1$.
$\overline {r}_v(1)=\overline {\rho }_1$.
(ii) The difference to part (i) is that ![]() $R_{\overline {\rho }_2}^{\psi \varepsilon }$ is not formally smooth. It is clear that
$R_{\overline {\rho }_2}^{\psi \varepsilon }$ is not formally smooth. It is clear that ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi,\mathrm {JL}(\overline {\rho }_2))=0$ for
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi,\mathrm {JL}(\overline {\rho }_2))=0$ for ![]() $\chi \notin W_D(\overline {\rho }_2)$. For the vanishing of
$\chi \notin W_D(\overline {\rho }_2)$. For the vanishing of ![]() $\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\mathrm {JL}(\overline {\rho }_2))$, choose a set of generators
$\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\chi,\mathrm {JL}(\overline {\rho }_2))$, choose a set of generators ![]() $(f_1,\ldots,f_m)$ of
$(f_1,\ldots,f_m)$ of ![]() $\mathfrak {m}_{\overline {r}_2}$, then they induce an exact sequence (recall assumption (H))
$\mathfrak {m}_{\overline {r}_2}$, then they induce an exact sequence (recall assumption (H))
 \[ 0\rightarrow \mathrm{JL}(\overline{\rho}_2)\rightarrow \Pi_2\rightarrow \prod_{i=1}^m\Pi_2, \]
\[ 0\rightarrow \mathrm{JL}(\overline{\rho}_2)\rightarrow \Pi_2\rightarrow \prod_{i=1}^m\Pi_2, \]
where ![]() $\Pi _2:=\widetilde {H}^1 (U^{v} , \mathbb {F})_{\mathfrak {m}_{\overline {r}_2}}$. Since
$\Pi _2:=\widetilde {H}^1 (U^{v} , \mathbb {F})_{\mathfrak {m}_{\overline {r}_2}}$. Since ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi,\Pi _2)=0$ and since
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\chi,\Pi _2)=0$ and since ![]() $\Pi _2$ is an injective representation of
$\Pi _2$ is an injective representation of ![]() $\mathcal {O}_D^{\times }/Z_D^1$ by Theorem 7.2(ii), the result easily follows.
$\mathcal {O}_D^{\times }/Z_D^1$ by Theorem 7.2(ii), the result easily follows.
Thanks to Theorem 8.26, we write ![]() $V$ for
$V$ for ![]() $V_1$ and
$V_1$ and ![]() $V_2$ from now on.
$V_2$ from now on.
Corollary 8.28 There exists a short exact sequence
Proof. This is a direct consequence of the proof of Theorem 8.26.
Corollary 8.29 The following statements hold:
(i)
 $V_{\rm fd}=0$ and
$V_{\rm fd}=0$ and  $\mathrm {soc}_{D^{\times }}(V)\cong \operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }} \alpha$;
$\mathrm {soc}_{D^{\times }}(V)\cong \operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }} \alpha$;(ii)
 $\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{D^{\times }/Z_D}(\operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }} \alpha,V)=1$;
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{D^{\times }/Z_D}(\operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }} \alpha,V)=1$;(iii)
 $\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{D^{\times }/Z_D}(\mathbf {1}_{D^{\times }},V)=2$.
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{D^{\times }/Z_D}(\mathbf {1}_{D^{\times }},V)=2$.
Proof. (i) The first assertion is just Corollary 8.23(iv). For the second assertion, by Frobenius reciprocity it suffices to show ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\alpha,V)$ has dimension
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\alpha,V)$ has dimension ![]() $1$. We take
$1$. We take ![]() $\overline {\rho }_1$ to be très ramifié. By Theorem 6.1, we have
$\overline {\rho }_1$ to be très ramifié. By Theorem 6.1, we have ![]() $\chi \in W_D(\overline {\rho }_1)$ if and only if
$\chi \in W_D(\overline {\rho }_1)$ if and only if ![]() $\chi = \mathbf {1}_{\mathcal {O}_D^{\times }}$, so that
$\chi = \mathbf {1}_{\mathcal {O}_D^{\times }}$, so that ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\alpha,\mathrm {JL}(\overline {\rho }_1))=0$. Hence, by applying
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\alpha,\mathrm {JL}(\overline {\rho }_1))=0$. Hence, by applying ![]() $\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\alpha,-)$ to (8.31) we obtain a long exact sequence
$\operatorname {{\mathrm {Hom}}}_{\mathcal {O}_D^{\times }}(\alpha,-)$ to (8.31) we obtain a long exact sequence
 \begin{align} & 0\rightarrow \operatorname{{\mathrm{Hom}}}(\alpha,V)\rightarrow \operatorname{{\mathrm{Ext}}}^1(\alpha,\mathbf{1}_{\mathcal{O}_D^{\times}})\rightarrow \operatorname{{\mathrm{Ext}}}^1(\alpha,\mathrm{JL}(\overline{\rho}_1))\rightarrow \operatorname{{\mathrm{Ext}}}^1(\alpha,V) \nonumber\\ &\quad {\buildrel {\partial} \over \longrightarrow} \operatorname{{\mathrm{Ext}}}^2(\alpha,\mathbf{1}_{\mathcal{O}_D^{\times}})\rightarrow \operatorname{{\mathrm{Ext}}}^2(\alpha,\mathrm{JL}(\overline{\rho}_1)), \end{align}
\begin{align} & 0\rightarrow \operatorname{{\mathrm{Hom}}}(\alpha,V)\rightarrow \operatorname{{\mathrm{Ext}}}^1(\alpha,\mathbf{1}_{\mathcal{O}_D^{\times}})\rightarrow \operatorname{{\mathrm{Ext}}}^1(\alpha,\mathrm{JL}(\overline{\rho}_1))\rightarrow \operatorname{{\mathrm{Ext}}}^1(\alpha,V) \nonumber\\ &\quad {\buildrel {\partial} \over \longrightarrow} \operatorname{{\mathrm{Ext}}}^2(\alpha,\mathbf{1}_{\mathcal{O}_D^{\times}})\rightarrow \operatorname{{\mathrm{Ext}}}^2(\alpha,\mathrm{JL}(\overline{\rho}_1)), \end{align}
where ![]() $\operatorname {{\mathrm {Ext}}}^i$ means
$\operatorname {{\mathrm {Ext}}}^i$ means ![]() $\operatorname {{\mathrm {Ext}}}^i_{\mathcal {O}_D^{\times }/Z_D^1}$. Since
$\operatorname {{\mathrm {Ext}}}^i_{\mathcal {O}_D^{\times }/Z_D^1}$. Since ![]() $\alpha \notin W_D(\overline {\rho }_1)$, see Theorem 6.1(ii)(a), we have
$\alpha \notin W_D(\overline {\rho }_1)$, see Theorem 6.1(ii)(a), we have ![]() $\operatorname {{\mathrm {Ext}}}^1(\alpha,\mathrm {JL}(\overline {\rho }_1))=0$ by Lemma 8.27(i). The result follows as
$\operatorname {{\mathrm {Ext}}}^1(\alpha,\mathrm {JL}(\overline {\rho }_1))=0$ by Lemma 8.27(i). The result follows as ![]() $\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1(\alpha,\mathbf {1}_{\mathcal {O}_D^{\times }})=1$ by Proposition 2.13.
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1(\alpha,\mathbf {1}_{\mathcal {O}_D^{\times }})=1$ by Proposition 2.13.
(ii) By Frobenius reciprocity, it is equivalent to proving ![]() $\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\alpha,V)=1$. Since
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^1_{\mathcal {O}_D^{\times }/Z_D^1}(\alpha,V)=1$. Since ![]() $\alpha \notin W_D(\overline {\rho }_1)$ (again we take
$\alpha \notin W_D(\overline {\rho }_1)$ (again we take ![]() $\overline {\rho }_1$ to be très ramifié), Lemma 8.27(i) implies that the map
$\overline {\rho }_1$ to be très ramifié), Lemma 8.27(i) implies that the map ![]() $\partial$ in (8.32) is an isomorphism. On the other hand, using Propositions 2.13 and 2.14 we know that
$\partial$ in (8.32) is an isomorphism. On the other hand, using Propositions 2.13 and 2.14 we know that ![]() $\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^2_{\mathcal {O}_D^{\times }/Z_D^1}(\alpha,\mathbf {1}_{\mathcal {O}_D^{\times }})=1$, from which the assertion follows.
$\dim _{\mathbb {F}}\operatorname {{\mathrm {Ext}}}^2_{\mathcal {O}_D^{\times }/Z_D^1}(\alpha,\mathbf {1}_{\mathcal {O}_D^{\times }})=1$, from which the assertion follows.
(iii) Note that ![]() $\mathbf {1}_{\mathcal {O}_D^{\times }}\notin W_D(\overline {\rho }_2)$, see (8.30). Using Lemma 8.27(ii) this implies
$\mathbf {1}_{\mathcal {O}_D^{\times }}\notin W_D(\overline {\rho }_2)$, see (8.30). Using Lemma 8.27(ii) this implies
hence by Frobenius reciprocity ![]() $\operatorname {{\mathrm {Ext}}}^i_{D^{\times }/Z_D}(\operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\mathbf {1},\mathrm {JL}(\overline {\rho }_2))=0$ for
$\operatorname {{\mathrm {Ext}}}^i_{D^{\times }/Z_D}(\operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\mathbf {1},\mathrm {JL}(\overline {\rho }_2))=0$ for ![]() $i=0,1$. Since
$i=0,1$. Since ![]() $\mathbf {1}_{D^{\times }}$ is a direct summand of
$\mathbf {1}_{D^{\times }}$ is a direct summand of ![]() $\operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\mathbf {1}$ as
$\operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\mathbf {1}$ as ![]() $[D^{\times }:\mathcal {O}_D^{\times }Z_D]=2$ and
$[D^{\times }:\mathcal {O}_D^{\times }Z_D]=2$ and ![]() $p>2$, we deduce
$p>2$, we deduce
Now, applying ![]() $\operatorname {{\mathrm {Hom}}}_{D^{\times }}(\mathbf {1}_{D^{\times }},-)$ to
$\operatorname {{\mathrm {Hom}}}_{D^{\times }}(\mathbf {1}_{D^{\times }},-)$ to ![]() $0\rightarrow V\rightarrow \mathrm {JL}(\overline {\rho }_2)\rightarrow (\mathbf {1}_{D^{\times }})^{\oplus 2}\rightarrow 0$ gives the result.
$0\rightarrow V\rightarrow \mathrm {JL}(\overline {\rho }_2)\rightarrow (\mathbf {1}_{D^{\times }})^{\oplus 2}\rightarrow 0$ gives the result.
Together with Theorem 6.1, we deduce the ![]() $D^{\times }$-socle of
$D^{\times }$-socle of ![]() $\mathrm {JL}(\overline {\rho }_i)$.
$\mathrm {JL}(\overline {\rho }_i)$.
(i) If
 $\overline {\rho }_1$ is peu ramifié, then
$\overline {\rho }_1$ is peu ramifié, then  $\operatorname {{\mathrm {soc}}}_{D^{\times }}\mathrm {JL}(\overline {\rho }_1)\cong \mathbf {1}_{D^{\times }}\oplus \operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\alpha$; if
$\operatorname {{\mathrm {soc}}}_{D^{\times }}\mathrm {JL}(\overline {\rho }_1)\cong \mathbf {1}_{D^{\times }}\oplus \operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\alpha$; if  $\overline {\rho }_1$ is très ramifié, then
$\overline {\rho }_1$ is très ramifié, then  $\operatorname {{\mathrm {soc}}}_{D^{\times }}\mathrm {JL}(\overline {\rho }_1)\cong \mathbf {1}_{D^{\times }}$.
$\operatorname {{\mathrm {soc}}}_{D^{\times }}\mathrm {JL}(\overline {\rho }_1)\cong \mathbf {1}_{D^{\times }}$.(ii) We have
 $\operatorname {{\mathrm {soc}}}_{D^{\times }}\mathrm {JL}(\overline {\rho }_2)\cong \operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\alpha$.
$\operatorname {{\mathrm {soc}}}_{D^{\times }}\mathrm {JL}(\overline {\rho }_2)\cong \operatorname {{\mathrm {Ind}}}_{\mathcal {O}_D^{\times }Z_D}^{D^{\times }}\alpha$.
Remark 8.31 Unlike the generic case treated in § 8.2, we see that ![]() $\mathrm {JL}(\overline {\rho }_1)$ detects the extension type of
$\mathrm {JL}(\overline {\rho }_1)$ detects the extension type of ![]() $\overline {\rho }_1$.
$\overline {\rho }_1$.
We also deduce from Corollary 8.30 that ![]() $\operatorname {{\mathrm {soc}}}_{\mathcal {O}_D^{\times }}\mathrm {JL}(\overline {\rho }_1)$ and
$\operatorname {{\mathrm {soc}}}_{\mathcal {O}_D^{\times }}\mathrm {JL}(\overline {\rho }_1)$ and ![]() $\operatorname {{\mathrm {soc}}}_{\mathcal {O}_D^{\times }}\mathrm {JL}(\overline {\rho }_2)$ are multiplicity free. This corresponds to the fact that
$\operatorname {{\mathrm {soc}}}_{\mathcal {O}_D^{\times }}\mathrm {JL}(\overline {\rho }_2)$ are multiplicity free. This corresponds to the fact that ![]() $\operatorname {{\mathrm {soc}}}_{K}\pi (\overline {\rho }_1)$ and
$\operatorname {{\mathrm {soc}}}_{K}\pi (\overline {\rho }_1)$ and ![]() $\operatorname {{\mathrm {soc}}}_{K}\pi (\overline {\rho }_2)$ are multiplicity free, and seems to be a nontrivial fact.
$\operatorname {{\mathrm {soc}}}_{K}\pi (\overline {\rho }_2)$ are multiplicity free, and seems to be a nontrivial fact.
Remark 8.32 We can show that the kernel of ![]() $\mathcal {S}^1(\operatorname {{\mathrm {Sp}}})\twoheadrightarrow \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$ in Corollary 8.25(ii), which we denote by
$\mathcal {S}^1(\operatorname {{\mathrm {Sp}}})\twoheadrightarrow \omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$ in Corollary 8.25(ii), which we denote by ![]() $U$, is
$U$, is ![]() $\mathbf {1}_{G_{\mathbb {Q}_p}}$-typic, i.e. it does not admit self-extensions of
$\mathbf {1}_{G_{\mathbb {Q}_p}}$-typic, i.e. it does not admit self-extensions of ![]() $\mathbf {1}_{G_{\mathbb {Q}_p}}$ as subquotients when restricted to
$\mathbf {1}_{G_{\mathbb {Q}_p}}$ as subquotients when restricted to ![]() $G_{\mathbb {Q}_p}$. Indeed, take
$G_{\mathbb {Q}_p}$. Indeed, take ![]() $\overline {\rho }_1$ to be très ramifié and
$\overline {\rho }_1$ to be très ramifié and ![]() $\overline {\rho }_1'$ to be peu ramifié, we obtain two embeddings
$\overline {\rho }_1'$ to be peu ramifié, we obtain two embeddings
from (8.13). One checks that
 \begin{gather*} 0\rightarrow \mathrm{Im}(i)\rightarrow U\rightarrow \mathbf{1}_{G_{\mathbb{Q}_p}}\otimes\mathrm{JL}(\overline{\rho}_1)\rightarrow0,\\ 0\rightarrow \mathrm{Im}(i')\rightarrow U\rightarrow \mathbf{1}_{G_{\mathbb{Q}_p}}\otimes \mathrm{JL}(\overline{\rho}_1')\rightarrow0. \end{gather*}
\begin{gather*} 0\rightarrow \mathrm{Im}(i)\rightarrow U\rightarrow \mathbf{1}_{G_{\mathbb{Q}_p}}\otimes\mathrm{JL}(\overline{\rho}_1)\rightarrow0,\\ 0\rightarrow \mathrm{Im}(i')\rightarrow U\rightarrow \mathbf{1}_{G_{\mathbb{Q}_p}}\otimes \mathrm{JL}(\overline{\rho}_1')\rightarrow0. \end{gather*}
As a consequence, ![]() $\mathrm {Im}(i)\neq \mathrm {Im}(i')$ because
$\mathrm {Im}(i)\neq \mathrm {Im}(i')$ because ![]() $\mathrm {JL}(\overline {\rho }_1)$ and
$\mathrm {JL}(\overline {\rho }_1)$ and ![]() $\mathrm {JL}(\overline {\rho }_1')$ are non-isomorphic by Corollary 8.30(i). It is then easy to deduce that
$\mathrm {JL}(\overline {\rho }_1')$ are non-isomorphic by Corollary 8.30(i). It is then easy to deduce that ![]() $U$ is isomorphic to
$U$ is isomorphic to ![]() $\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes (\mathrm {JL}(\overline {\rho }_1)\times _{V}\mathrm {JL}(\overline {\rho }_1'))$, where the fibered product is taken with respect to (8.31).
$\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes (\mathrm {JL}(\overline {\rho }_1)\times _{V}\mathrm {JL}(\overline {\rho }_1'))$, where the fibered product is taken with respect to (8.31).
8.3.1 Summary
We summarize the results proved above in the following theorem.
Theorem 8.33 We have the following:
(i)
 $\mathcal {S}^0(\mathbf {1}_G)=\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }}$,
$\mathcal {S}^0(\mathbf {1}_G)=\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }}$,  $\mathcal {S}^1(\mathbf {1}_G)=0$,
$\mathcal {S}^1(\mathbf {1}_G)=0$,  $\mathcal {S}^2(\mathbf {1}_G)=\omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$;
$\mathcal {S}^2(\mathbf {1}_G)=\omega ^{-1}\otimes \mathbf {1}_{D^{\times }}$;(ii)
 $\mathcal {S}^0(\operatorname {{\mathrm {Sp}}})=\mathcal {S}^2(\operatorname {{\mathrm {Sp}}})=0$, and there exists a short exact sequence
$\mathcal {S}^0(\operatorname {{\mathrm {Sp}}})=\mathcal {S}^2(\operatorname {{\mathrm {Sp}}})=0$, and there exists a short exact sequence
 \[ 0\rightarrow (\mathbf{1}_{G_{\mathbb{Q}_p}}\otimes\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow \mathcal{S}^1(\operatorname{{\mathrm{Sp}}}) \rightarrow (\mathbf{1}_{G_{\mathbb{Q}_p}}\otimes V)\oplus (\omega^{-1}\otimes\mathbf{1}_{D^{\times}})\rightarrow0; \]
\[ 0\rightarrow (\mathbf{1}_{G_{\mathbb{Q}_p}}\otimes\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow \mathcal{S}^1(\operatorname{{\mathrm{Sp}}}) \rightarrow (\mathbf{1}_{G_{\mathbb{Q}_p}}\otimes V)\oplus (\omega^{-1}\otimes\mathbf{1}_{D^{\times}})\rightarrow0; \]
(iii)
 $\mathcal {S}^0(\pi _{\alpha })=\mathcal {S}^2(\pi _{\alpha })=0$ and there exists a short exact sequence
$\mathcal {S}^0(\pi _{\alpha })=\mathcal {S}^2(\pi _{\alpha })=0$ and there exists a short exact sequence
 \[ 0\rightarrow \omega^{-1}\otimes V\rightarrow \mathcal{S}^1(\pi_{\alpha})\rightarrow \omega^{-1}\otimes \mathbf{1}_{D^{\times}}\rightarrow0; \]
\[ 0\rightarrow \omega^{-1}\otimes V\rightarrow \mathcal{S}^1(\pi_{\alpha})\rightarrow \omega^{-1}\otimes \mathbf{1}_{D^{\times}}\rightarrow0; \]
(iv) there exist exact sequences
and \begin{align*} 0\rightarrow \mathbf{1}_{D^{\times}}\rightarrow \mathrm{JL}(\overline{\rho}_1)\rightarrow V\rightarrow0 \end{align*}
moreover,
\begin{align*} 0\rightarrow \mathbf{1}_{D^{\times}}\rightarrow \mathrm{JL}(\overline{\rho}_1)\rightarrow V\rightarrow0 \end{align*}
moreover, \begin{align*} 0\rightarrow V\rightarrow \mathrm{JL}(\overline{\rho}_2)\rightarrow (\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow0; \end{align*}
\begin{align*} 0\rightarrow V\rightarrow \mathrm{JL}(\overline{\rho}_2)\rightarrow (\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow0; \end{align*}
 $\mathrm {JL}(\overline {\rho }_2)$ is isomorphic to the universal extension of
$\mathrm {JL}(\overline {\rho }_2)$ is isomorphic to the universal extension of  $(\mathbf {1}_{D^{\times }})^{\oplus 2}$ by
$(\mathbf {1}_{D^{\times }})^{\oplus 2}$ by  $V$.
$V$.
8.4 The non-minimal case
We briefly explain how to modify the arguments in §§ 8.2 and 8.3 to handle the non-minimal case (i.e. ![]() $d\neq 1$ in Theorem 7.7).
$d\neq 1$ in Theorem 7.7).
Let ![]() $\overline {\rho }=\overline {r}_v(1)$ and assume
$\overline {\rho }=\overline {r}_v(1)$ and assume ![]() $\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })=\mathbb {F}$; in particular,
$\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })=\mathbb {F}$; in particular, ![]() $\overline {\rho }$ is allowed to be irreducible. We put
$\overline {\rho }$ is allowed to be irreducible. We put
 \begin{equation}
\mathrm{JL}(\overline{\rho}):=\left\{\begin{array}{@{}lll}
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\chi\omega^{-1},\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{if}\ \overline{\rho}\sim \big(\begin{smallmatrix}
{\chi} & {*}\\ {0} & {\chi\omega}\end{smallmatrix}\big), \\
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\overline{\rho}(-1),\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{otherwise}. \end{array}\right.
\end{equation}
\begin{equation}
\mathrm{JL}(\overline{\rho}):=\left\{\begin{array}{@{}lll}
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\chi\omega^{-1},\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{if}\ \overline{\rho}\sim \big(\begin{smallmatrix}
{\chi} & {*}\\ {0} & {\chi\omega}\end{smallmatrix}\big), \\
\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\overline{\rho}(-1),\mathcal{S}^1(\pi(\overline{\rho})))
& \mathrm{otherwise}. \end{array}\right.
\end{equation}
(i) If
 $\overline {\rho }$ is not of the form
$\overline {\rho }$ is not of the form  $\big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$, then
and
$\big (\begin{smallmatrix} {\chi } & {*}\\ {0} & {\chi \omega }\end{smallmatrix}\big )$, then
and \[ \widetilde{H}^1 (U^{v},\mathbb{F})[\mathfrak{m}_{\overline{r}}]\cong (\overline{\rho}(-1)\otimes\mathrm{JL}(\overline{\rho}))^{\oplus d} \]
\[ \widetilde{H}^1 (U^{v},\mathbb{F})[\mathfrak{m}_{\overline{r}}]\cong (\overline{\rho}(-1)\otimes\mathrm{JL}(\overline{\rho}))^{\oplus d} \]
 $\mathcal {S}^1(\pi (\overline {\rho }))\cong \overline {\rho }(-1)\otimes \mathrm {JL}(\overline {\rho })$.
$\mathcal {S}^1(\pi (\overline {\rho }))\cong \overline {\rho }(-1)\otimes \mathrm {JL}(\overline {\rho })$.(ii) If
 $\overline {\rho }\sim \big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$, then
and there exists a short exact sequence
$\overline {\rho }\sim \big (\begin{smallmatrix} {1} & {*}\\ {0} & {\omega }\end{smallmatrix}\big )$, then
and there exists a short exact sequence \[ \widetilde{H}^1 (U^{v},\mathbb{F})[\mathfrak{m}_{\overline{r}}]\cong (\overline{\rho}(-1)\otimes\mathrm{JL}(\overline{\rho}))^{\oplus d}, \]
\[ \widetilde{H}^1 (U^{v},\mathbb{F})[\mathfrak{m}_{\overline{r}}]\cong (\overline{\rho}(-1)\otimes\mathrm{JL}(\overline{\rho}))^{\oplus d}, \]
 \[ 0\rightarrow \mathcal{S}^1(\pi(\overline{\rho})){\buildrel {f} \over \longrightarrow} \overline{\rho}(-1)\otimes\mathrm{JL}(\overline{\rho})\rightarrow (\mathbf{1}_{G_{\mathbb{Q}_p}}\otimes\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow0. \]
\[ 0\rightarrow \mathcal{S}^1(\pi(\overline{\rho})){\buildrel {f} \over \longrightarrow} \overline{\rho}(-1)\otimes\mathrm{JL}(\overline{\rho})\rightarrow (\mathbf{1}_{G_{\mathbb{Q}_p}}\otimes\mathbf{1}_{D^{\times}})^{\oplus 2}\rightarrow0. \]
Proof. (i) We claim that ![]() $\mathcal {S}^1(\widetilde {S}(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])=\widetilde {H}^1 (U^{v},\mathbb {F})[\mathfrak {m}_{\overline {r}}]$. If
$\mathcal {S}^1(\widetilde {S}(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])=\widetilde {H}^1 (U^{v},\mathbb {F})[\mathfrak {m}_{\overline {r}}]$. If ![]() $\overline {\rho }^{\rm ss}\nsim \chi \oplus \chi \omega$, it is proved in [Reference PaškūnasPaš22, Lemma 6.1]. If
$\overline {\rho }^{\rm ss}\nsim \chi \oplus \chi \omega$, it is proved in [Reference PaškūnasPaš22, Lemma 6.1]. If ![]() $\overline {\rho }^{\rm ss}\sim \chi \oplus \chi \omega$, then the assumption on
$\overline {\rho }^{\rm ss}\sim \chi \oplus \chi \omega$, then the assumption on ![]() $\overline {\rho }$ implies that
$\overline {\rho }$ implies that ![]() $R_{\overline {\rho }}^{\psi \varepsilon ^{-1}}$ is formally smooth, so we may apply Proposition 8.9 (using Corollary 7.9).
$R_{\overline {\rho }}^{\psi \varepsilon ^{-1}}$ is formally smooth, so we may apply Proposition 8.9 (using Corollary 7.9).
The claim implies that ![]() $\mathcal {S}^1(\widetilde {S}(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])$ is
$\mathcal {S}^1(\widetilde {S}(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}])$ is ![]() $\overline {\rho }(-1)$-typic. Since
$\overline {\rho }(-1)$-typic. Since ![]() $\widetilde {S} (U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]\cong \pi (\overline {\rho })^{\oplus d}$ by Theorem 7.7,
$\widetilde {S} (U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]\cong \pi (\overline {\rho })^{\oplus d}$ by Theorem 7.7, ![]() $\mathcal {S}^1(\pi (\overline {\rho }))$ is also
$\mathcal {S}^1(\pi (\overline {\rho }))$ is also ![]() $\overline {\rho }(-1)$-typic by Lemma 8.6(ii). The result easily follows.
$\overline {\rho }(-1)$-typic by Lemma 8.6(ii). The result easily follows.
(ii) First, the proof of Proposition 8.20 shows that
which implies
 \begin{align*} \operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\omega^{-1},\mathcal{S}^1(\widetilde{S} (U^{v}, \mathbb{F})[\mathfrak{m}_{\overline{r}}])) & \overset{\phi^*}{\xrightarrow{\sim}}\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\omega^{-1}, \widetilde{H}^1 (U^{v}, \mathbb{F})[\mathfrak{m}_{\overline{r}}])\\ &\simeq\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\overline{\rho}(-1),\widetilde{H}^1 (U^{v}, \mathbb{F})[\mathfrak{m}_{\overline{r}}]), \end{align*}
\begin{align*} \operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\omega^{-1},\mathcal{S}^1(\widetilde{S} (U^{v}, \mathbb{F})[\mathfrak{m}_{\overline{r}}])) & \overset{\phi^*}{\xrightarrow{\sim}}\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\omega^{-1}, \widetilde{H}^1 (U^{v}, \mathbb{F})[\mathfrak{m}_{\overline{r}}])\\ &\simeq\operatorname{{\mathrm{Hom}}}_{G_{\mathbb{Q}_p}}(\overline{\rho}(-1),\widetilde{H}^1 (U^{v}, \mathbb{F})[\mathfrak{m}_{\overline{r}}]), \end{align*}
where the second isomorphism holds because ![]() $\widetilde {H}^1(U^{v},\mathbb {F})[\mathfrak {m}_{\overline {r}}]$ is
$\widetilde {H}^1(U^{v},\mathbb {F})[\mathfrak {m}_{\overline {r}}]$ is ![]() $\overline {\rho }(-1)$-typic. Choose an isomorphism
$\overline {\rho }(-1)$-typic. Choose an isomorphism ![]() $\iota : \pi (\overline {\rho })^{\oplus d}\xrightarrow {\sim } \widetilde {S}(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$; it induces an isomorphism
$\iota : \pi (\overline {\rho })^{\oplus d}\xrightarrow {\sim } \widetilde {S}(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$; it induces an isomorphism
Thus, we get an isomorphism
as desired. Let ![]() $f'$ be the composite map
$f'$ be the composite map
Since ![]() $\mathcal {S}^1(\pi (\overline {\rho }))$ is contained in
$\mathcal {S}^1(\pi (\overline {\rho }))$ is contained in ![]() $\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$ which is
$\widetilde {H}^1(U^{v}, \mathbb {F})[\mathfrak {m}_{\overline {r}}]$ which is ![]() $\overline {\rho }(-1)$-typic, we may apply Lemma 8.35 below to obtain an embedding
$\overline {\rho }(-1)$-typic, we may apply Lemma 8.35 below to obtain an embedding
extending the natural embedding ![]() $\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho })\hookrightarrow \overline {\rho }(-1)\otimes \mathrm {JL}(\overline {\rho })$. Moreover,
$\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho })\hookrightarrow \overline {\rho }(-1)\otimes \mathrm {JL}(\overline {\rho })$. Moreover, ![]() $f$ is
$f$ is ![]() $G_{\mathbb {Q}_{p}}\times D^{\times }$-equivariant by construction. We are left to show
$G_{\mathbb {Q}_{p}}\times D^{\times }$-equivariant by construction. We are left to show ![]() $\mathrm {Coker}(f)\cong (\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2}$. It is clear that
$\mathrm {Coker}(f)\cong (\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2}$. It is clear that ![]() $f^{\oplus d}$ and
$f^{\oplus d}$ and ![]() $f'$ coincide when restricted to
$f'$ coincide when restricted to ![]() $\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho })^{\oplus d}$, so
$\omega ^{-1}\otimes \mathrm {JL}(\overline {\rho })^{\oplus d}$, so ![]() $f'=f^{\oplus d}$ by the uniqueness part of Lemma 8.35. Since
$f'=f^{\oplus d}$ by the uniqueness part of Lemma 8.35. Since ![]() $\operatorname {{\mathrm {Coker}}}(f')\cong (\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2d}$, we obtain
$\operatorname {{\mathrm {Coker}}}(f')\cong (\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2d}$, we obtain ![]() $\mathrm {Coker}(f)\cong (\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2}$ as required.
$\mathrm {Coker}(f)\cong (\mathbf {1}_{G_{\mathbb {Q}_p}}\otimes \mathbf {1}_{D^{\times }})^{\oplus 2}$ as required.
Lemma 8.35 Let ![]() $\overline {\rho }\sim \big (\begin{smallmatrix} {\chi _1} & {*}\\ {0} & {\chi _2}\end{smallmatrix}\big )$ with
$\overline {\rho }\sim \big (\begin{smallmatrix} {\chi _1} & {*}\\ {0} & {\chi _2}\end{smallmatrix}\big )$ with ![]() $\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })\cong \mathbb {F}$. If
$\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })\cong \mathbb {F}$. If ![]() $M$ is a
$M$ is a ![]() $\overline {\rho }$-typic
$\overline {\rho }$-typic ![]() $\mathbb {F}[G_{\mathbb {Q}_p}]$-module, then for any submodule
$\mathbb {F}[G_{\mathbb {Q}_p}]$-module, then for any submodule ![]() $M'\subset M$ there exists a unique embedding
$M'\subset M$ there exists a unique embedding
extending the embedding ![]() $\chi _1\otimes \operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M')\hookrightarrow \overline {\rho }\otimes \operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M')$ induced from
$\chi _1\otimes \operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M')\hookrightarrow \overline {\rho }\otimes \operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M')$ induced from ![]() $\chi _1\hookrightarrow \overline {\rho }$.
$\chi _1\hookrightarrow \overline {\rho }$.
Proof. Since ![]() $M$ is
$M$ is ![]() $\overline {\rho }$-typic, it is naturally isomorphic to
$\overline {\rho }$-typic, it is naturally isomorphic to ![]() $\overline {\rho }\otimes M_0$ where
$\overline {\rho }\otimes M_0$ where ![]() $M_0:=\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\overline {\rho },M)$. Actually, the assumption on
$M_0:=\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\overline {\rho },M)$. Actually, the assumption on ![]() $\overline {\rho }$ implies that
$\overline {\rho }$ implies that ![]() $M_0= \operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M)$. Writing
$M_0= \operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M)$. Writing ![]() $M'_0:=\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M')$, we claim that
$M'_0:=\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,M')$, we claim that ![]() $M'$ is contained in
$M'$ is contained in ![]() $\overline {\rho }\otimes M_0'$, both regarded as subspaces of
$\overline {\rho }\otimes M_0'$, both regarded as subspaces of ![]() $\overline {\rho }\otimes M_0$. Indeed, letting
$\overline {\rho }\otimes M_0$. Indeed, letting ![]() $\widetilde {M}':=M'+\overline {\rho }\otimes M_0'$, we need to prove
$\widetilde {M}':=M'+\overline {\rho }\otimes M_0'$, we need to prove ![]() $\widetilde {M}'=\overline {\rho }\otimes M_0'$. It is clear that
$\widetilde {M}'=\overline {\rho }\otimes M_0'$. It is clear that ![]() $\chi _1\otimes M_0'$ is identified with
$\chi _1\otimes M_0'$ is identified with ![]() $M'\cap (\chi _1\otimes M_0)$, thus
$M'\cap (\chi _1\otimes M_0)$, thus ![]() $M'/(\chi _1\otimes M_0')$ embeds in
$M'/(\chi _1\otimes M_0')$ embeds in ![]() $\chi _2\otimes M_0$ and is
$\chi _2\otimes M_0$ and is ![]() $\chi _2$-typic. Using the natural isomorphism
$\chi _2$-typic. Using the natural isomorphism ![]() $\widetilde {M}'/(\overline {\rho }\otimes M_0')\cong M'/(M'\cap (\overline {\rho }\otimes M_0'))$, we see that
$\widetilde {M}'/(\overline {\rho }\otimes M_0')\cong M'/(M'\cap (\overline {\rho }\otimes M_0'))$, we see that ![]() $\widetilde {M}'/(\overline {\rho }\otimes M_0')$ is a quotient of
$\widetilde {M}'/(\overline {\rho }\otimes M_0')$ is a quotient of ![]() $M'/(\chi _1\otimes M_0')$, thus
$M'/(\chi _1\otimes M_0')$, thus
On the other hand, if ![]() $\widetilde {M}'/(\overline {\rho }\otimes M_0')$ is nonzero, then it embeds in
$\widetilde {M}'/(\overline {\rho }\otimes M_0')$ is nonzero, then it embeds in ![]() $\overline {\rho }\otimes (M_0/M_0')$ and we must have
$\overline {\rho }\otimes (M_0/M_0')$ and we must have ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,\widetilde {M}'/(\overline {\rho }\otimes M_0'))\neq 0$, a contradiction.
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(\chi _1,\widetilde {M}'/(\overline {\rho }\otimes M_0'))\neq 0$, a contradiction.
The claim implies that the given inclusion ![]() $M'\subset M$ provides an embedding required in the lemma, so we are left to prove the uniqueness.
$M'\subset M$ provides an embedding required in the lemma, so we are left to prove the uniqueness.
Consider the exact sequence
with ![]() $Q$ being the quotient. As seen above,
$Q$ being the quotient. As seen above, ![]() $Q$ is
$Q$ is ![]() $\chi _2$-typic. Applying
$\chi _2$-typic. Applying ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(-,\overline {\rho }\otimes M_0')$ to it, we obtain an exact sequence
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(-,\overline {\rho }\otimes M_0')$ to it, we obtain an exact sequence
The result follows because ![]() $\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(Q,\overline {\rho }\otimes M_0')=0$ (as
$\operatorname {{\mathrm {Hom}}}_{G_{\mathbb {Q}_p}}(Q,\overline {\rho }\otimes M_0')=0$ (as ![]() $Q$ is
$Q$ is ![]() $\chi _2$-typic).
$\chi _2$-typic).
Using Proposition 8.34, the arguments in §§ 8.2 and 8.3 when ![]() $\overline {\rho }$ is reducible with
$\overline {\rho }$ is reducible with ![]() $\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })=\mathbb {F}$, taking into account multiplicities everywhere, go through and give similar results in the non-minimal case as in Theorems 8.12, 8.26 and 8.33.
$\operatorname {{\mathrm {End}}}_{G_{\mathbb {Q}_p}}(\overline {\rho })=\mathbb {F}$, taking into account multiplicities everywhere, go through and give similar results in the non-minimal case as in Theorems 8.12, 8.26 and 8.33.
Remark 8.36 If ![]() $\overline {\rho }_0=\chi _1\oplus \chi _2$ with
$\overline {\rho }_0=\chi _1\oplus \chi _2$ with ![]() $\chi _1\chi _2^{-1}\neq \mathbf {1},\omega ^{\pm 1}$, we put
$\chi _1\chi _2^{-1}\neq \mathbf {1},\omega ^{\pm 1}$, we put
Combining with Proposition 8.34, the proof of Theorem 8.12 shows ![]() $\mathcal {S}^1(\pi (\overline {\rho }_0))=\overline {\rho }_0(-1)\otimes \mathrm {JL}(\overline {\rho }_0)$.
$\mathcal {S}^1(\pi (\overline {\rho }_0))=\overline {\rho }_0(-1)\otimes \mathrm {JL}(\overline {\rho }_0)$.
Acknowledgements
We thank Yiwen Ding, Andrea Dotto and Vytautas Paškūnas for several interesting discussions during the preparation of this paper, and we thank Dingxin Zhang and Weizhe Zheng for answering our questions. We would like to thank Christophe Breuil and Florian Herzig for their comments on an earlier version. We are grateful to Judith Ludwig for her help with the proof of Theorem 7.1(iii). We are also grateful to the anonymous referee for several helpful corrections and suggestions. Y.H. has presented this work at Beijing International Center for Mathematical Research in November 2021, and he thanks Yiwen Ding for the invitation. It will be obvious to the reader that this work is largely inspired by the previous work [Reference Breuil, Herzig, Hu, Morra and SchraenBHHMS23, Reference PaškūnasPaš22].
Conflicts of interest
None.
Financial support
H.W. is partially supported by the National Key R&D Program of China (grant number 2023YFA1009702) and National Natural Science Foundation of China (grant numbers 12371011 and 11971028). Y.H. is partially supported by the National Key R&D Program of China (grant number 2020YFA0712600), CAS Project for Young Scientists in Basic Research (grant number YSBR-033), National Natural Science Foundation of China (grant numbers 12288201 and 11971028), National Center for Mathematics and Interdisciplinary Sciences and Hua Loo-Keng Key Laboratory of Mathematics, Chinese Academy of Sciences.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.