No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 March 2025
Without using the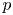 
$p$-adic Langlands correspondence, we prove that for many finite-length smooth representations of 
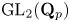$\mathrm {GL}_2(\mathbf {Q}_p)$ on 
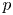$p$-torsion modules the 
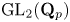$\mathrm {GL}_2(\mathbf {Q}_p)$-linear morphisms coincide with the morphisms that are linear for the normalizer of a parahoric subgroup. We identify this subgroup to be the Iwahori subgroup in the supersingular case, and 
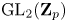$\mathrm {GL}_2(\mathbf {Z}_p)$ in the principal series case. As an application, we relate the action of parahoric subgroups to the action of the inertia group of 
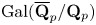$\mathrm {Gal}(\overline {\mathbf {Q}}_p/\mathbf {Q}_p)$, and we prove that if an irreducible Banach space representation 
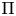$\Pi$ of 
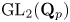$\mathrm {GL}_2(\mathbf {Q}_p)$ has infinite 
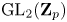$\mathrm {GL}_2(\mathbf {Z}_p)$-length, then a twist of 
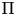$\Pi$ has locally algebraic vectors. This answers a question of Dospinescu. We make the simplifying assumption that 
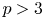$p > 3$ and that all our representations are generic.
${\rm GL_2}$ of a local field, Duke Math. J. 75 (1994), 261–292; MR 1290194.Google Scholar
$p$-adiques de 
${\rm GL}_2({\rm Q}_p)$. I, Compos. Math. 138 (2003), 165–188; MR 2018825.CrossRefGoogle Scholar
$p$-adiques de 
${\rm GL}_2({\rm Q}_p)$. II, J. Inst. Math. Jussieu 2 (2003), 23–58; MR 1955206.Google Scholar
$p$ Langlands correspondence for 
${\rm GL_2}$, Mem. Amer. Math. Soc. 216 (2012); MR 2931521.Google Scholar
${\rm GL}_{2}(k)$ to 
${\rm GL}_{2}(\mathfrak {o})$, Math. Ann. 206 (1973), 311–318; MR 0338274.Google Scholar
${\rm GL}_2(\Bbb {Q}_p)$, Algebra Number Theory 8 (2014), 1447–1519; MR 3267142.CrossRefGoogle Scholar
$p$ representations of quaternion algebra over 
$\mathbb {Q}_p$, Preprint (2022), arXiv:2201.01464.Google Scholar
$p$-adic and mod 
$p$ representations of quaternion algebra over 
$\mathbb {Q}_p$, J. Reine Angew. Math. 812 (2024), 163–210.Google Scholar
${\rm GL_2}({\rm Q}_p)$-representations over 
$\overline {\boldsymbol F}_p$, J. Algebra 339 (2011), 252–303; MR 2811322.Google Scholar
$p$-modular representations of 
${\rm GL}_2({\rm Q}_p)$, Trans. Amer. Math. Soc. 365 (2013), 6625–6667; MR 3105765.Google Scholar
${\rm GL}_2({\rm Q}_p)$, Doc. Math. 22 (2017), 777–823; MR 3650223.Google Scholar
${\rm GL_2}(\mathbb {Q}_p)$, Astérisque 331 (2010), 317–353; MR 2667891.Google Scholar
${\rm SL}_{2}$, Astérisque, No. 46, Société Mathématique de France, Paris, 1977, Avec un sommaire anglais, Rédigé avec la collaboration de Hyman Bass; MR 0476875.Google ScholarTo send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.