Hostname: page-component-6587cd75c8-ptrpl Total loading time: 0 Render date: 2025-04-24T02:52:44.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Modulo ℓ distinction problems

Part of: Lie groups

Published online by Cambridge University Press:  30 September 2024

Peiyi Cui ,
Thomas Lanard Open the ORCID record for Thomas Lanard [Opens in a new window]  and
Hengfei Lu
Peiyi Cui
Affiliation:
Morningside Center of Mathematics, Chinese Academy of Sciences, Zhongguancun East Road, Haidian District, Beijing 100190, PR China peiyi.cuimath@gmail.com
Thomas Lanard
Affiliation:
CNRS, Laboratoire de mathématiques de Versailles, Université Paris-Saclay, UVSQ, 78000 Versailles, France thomas.lanard@uvsq.fr
Hengfei Lu
Affiliation:
School of Mathematical Sciences, Beihang University, 9 Nansan Street, Shahe Higher Education Park, Changping, Beijing 102206, PR China luhengfei@buaa.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 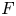$F$ be a non-archimedean local field of characteristic different from 2 and residual characteristic 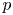$p$. This paper concerns the 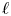$\ell$-modular representations of a connected reductive group 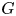$G$ distinguished by a Galois involution, with 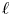$\ell$ an odd prime different from 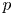$p$. We start by proving a general theorem allowing to lift supercuspidal 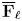$\overline {\mathbf {F}}_{\ell }$-representations of 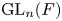$\operatorname {GL}_n(F)$ distinguished by an arbitrary closed subgroup 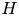$H$ to a distinguished supercuspidal 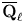$\overline {\mathbf {Q}}_{\ell }$-representation. Given a quadratic field extension 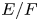$E/F$ and an irreducible 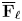$\overline {\mathbf {F}}_{\ell }$-representation 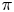$\pi$ of 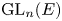$\operatorname {GL}_n(E)$, we verify the Jacquet conjecture in the modular setting that if the Langlands parameter 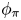$\phi _\pi$ is irreducible and conjugate-selfdual, then 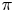$\pi$ is either 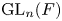$\operatorname {GL}_n(F)$-distinguished or 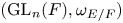$(\operatorname {GL}_{n}(F),\omega _{E/F})$-distinguished (where 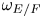$\omega _{E/F}$ is the quadratic character of 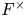$F^\times$ associated to the quadratic field extension 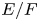$E/F$ by the local class field theory), but not both, which extends one result of Sécherre to the case 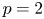$p=2$. We give another application of our lifting theorem for supercuspidal representations distinguished by a unitary involution, extending one result of Zou to 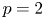$p=2$. After that, we give a complete classification of the 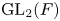$\operatorname {GL}_2(F)$-distinguished representations of 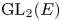$\operatorname {GL}_2(E)$. Using this classification we discuss a modular version of the Prasad conjecture for 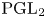$\operatorname {PGL}_2$. We show that the ‘classical’ Prasad conjecture fails in the modular setting. We propose a solution using non-nilpotent Weil–Deligne representations. Finally, we apply the restriction method of Anandavardhanan and Prasad to classify the 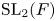$\operatorname {SL}_2(F)$-distinguished modular representations of 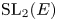$\operatorname {SL}_2(E)$.

Keywords

modular representationdistinction problemPrasad's conjecture

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 10 , October 2024 , pp. 2285 - 2321
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anandavardhanan, U. K., Kurinczuk, R., Matringe, N., Sécherre, V. and Stevens, S., Galois self-dual cuspidal types and Asai local factors, J. Eur. Math. Soc. (JEMS) 23 (2021), 3129–3191.CrossRefGoogle Scholar
Anandavardhanan, U. K. and Prasad, D., Distinguished representations for ${\rm SL} (2)$, Math. Res. Lett. 10 (2003), 867–878.CrossRefGoogle Scholar
Bourbaki, N., Integration. II. Chapters 7–9, Elements of Mathematics (Berlin) (Springer, Berlin, 2004). Translated from the 1963 and 1969 French originals by Sterling K. Berberian.CrossRefGoogle Scholar
Bushnell, C. J. and Henniart, G., The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 335 (Springer, Berlin, 2006).CrossRefGoogle Scholar
Cui, P., Modulo $\ell$-representations of $p$-adic groups $\mathrm {SL}_n(F)$: maximal simple $k$-types, Preprint (2020), arXiv:2012.07492.Google Scholar
Drevon, B. and Sécherre, V., Décomposition en blocs de la catégorie des représentations $\ell$-modulaires lisses de longueur finie de ${\rm GL}_m(D)$, Ann. Inst. Fourier (Grenoble) 73 (2023), 2411–2468.CrossRefGoogle Scholar
Feigon, B., Lapid, E. and Offen, O., On representations distinguished by unitary groups, Publ. Math. Inst. Hautes Études Sci. 115 (2012), 185–323.CrossRefGoogle Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups, in Sur les Conjectures de Gross et Prasad. I, Astérisque, vol. 346 (Société mathématique de France, 2012), 1–109.Google Scholar
Gelbart, S. S. and Knapp, A. W., $L$-indistinguishability and $R$ groups for the special linear group, Adv. Math. 43 (1982), 101–121.CrossRefGoogle Scholar
Hakim, J., Character relations for distinguished representations, Amer. J. Math. 116 (1994), 1153–1202.CrossRefGoogle Scholar
Hakim, J. and Murnaghan, F., Globalization of distinguished supercuspidal representations of ${\rm GL}(n)$, Canad. Math. Bull. 45 (2002), 220–230.CrossRefGoogle Scholar
Helm, D., The Bernstein center of the category of smooth $W(k){\rm GL_n(F)}$-modules, Forum Math. Sigma 4 (2016), e11.CrossRefGoogle Scholar
Heumos, M. J. and Rallis, S., Symplectic-Whittaker models for ${\rm Gl_n}$, Pacific J. Math. 146 (1990), 247–279.CrossRefGoogle Scholar
Jo, Y., The local exterior square and Asai $L$-functions for $\mathrm {GL}(n)$ in odd characteristic, Pacific J. Math. 322 (2023), 301–340.CrossRefGoogle Scholar
Kable, A. C., Asai $L$-functions and Jacquet's conjecture, Amer. J. Math. 126 (2004), 789–820.CrossRefGoogle Scholar
Kurinczuk, R. and Matringe, N., Characterisation of the poles of the $\ell$-modular Asai ${\rm L}$-factor, Bull. Soc. Math. France 148 (2020), 481–514.CrossRefGoogle Scholar
Kurinczuk, R. and Matringe, N., The $\ell$-modular local langlands correspondence and local constants, J. Inst. Math. Jussieu 20 (2021), 1585–1635.CrossRefGoogle Scholar
Kurinczuk, R., Matringe, N. and Sécherre, V., Cuspidal $\ell$-modular representations of $\mathrm{GL}_n(F)$ distinguished by a Galois involution, Preprint (2023), arXiv:2310.15820.Google Scholar
Lu, H., Theta correspondence and the Prasad conjecture for ${\rm SL}(2)$, Pacific J. Math. 295 (2018), 477–498.CrossRefGoogle Scholar
Lu, H., The Prasad conjectures for ${\rm GSp_4}$ and ${\rm PGSp_4}$, Algebra Number Theory 14 (2020), 2417–2480.CrossRefGoogle Scholar
Mínguez, A. and Sécherre, V., Types modulo $\ell$ pour les formes intérieures de ${\rm GL_n}$ sur un corps local non archimédien, Proc. Lond. Math. Soc. (3) 109 (2014), 823–891, with an appendix by Vincent Sécherre et Shaun Stevens.CrossRefGoogle Scholar
Mínguez, A. and Sécherre, V., Correspondance de Jacquet-Langlands locale et congruences modulo $\ell$, Invent. Math. 208 (2017), 553–631.CrossRefGoogle Scholar
Neukirch, J., Algebraic number theory, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 322 (Springer, Berlin, 1999). Translated from the 1992 German original and with a note by Norbert Schappacher, With a foreword by G. Harder.CrossRefGoogle Scholar
Prasad, D., Invariant forms for representations of ${\rm GL_2}$ over a local field, Amer. J. Math. 114 (1992), 1317–1363.CrossRefGoogle Scholar
Prasad, D., A ‘relative’ local Langlands correspondence, Preprint (2015), arXiv:1512.04347.Google Scholar
Prasad, D., Generic representations for symmetric spaces, Adv. Math. 348 (2019), 378–411.CrossRefGoogle Scholar
Sakellaridis, Y. and Venkatesh, A., Periods and harmonic analysis on spherical varieties, Astérisque 396 (2017).Google Scholar
Sécherre, V., Supercuspidal representations of ${\rm GL_n}({\rm F})$ distinguished by a Galois involution, Algebra Number Theory 13 (2019), 1677–1733.CrossRefGoogle Scholar
Sécherre, V. and Venketasubramanian, C. G., Modular representations of ${\rm GL}(n)$ distinguished by ${\rm GL}(n-1)$ over a $p$-adic field, Int. Math. Res. Not. IMRN 2017 (2017), 4435–4492.Google Scholar
Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42 (Springer, New York-Heidelberg, 1977). Translated from the second French edition by Leonard L. Scott.CrossRefGoogle Scholar
Shelstad, D., Notes on L-indistinguishability (based on a lecture of R. P. Langlands), in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 193–203.Google Scholar
Vignéras, M.-F., Représentations modulaires de ${\rm GL}(2,F)$ en caractéristique $l,F$ corps $p$-adique, $p\neq l$, Compos. Math. 72 (1989), 33–66.Google Scholar
Vignéras, M.-F., Représentations l-modulaires d'un groupe réductif p-adique avec $l\ne p$, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, MA, 1996).Google Scholar
Vignéras, M.-F., Correspondance de Langlands semi-simple pour ${\rm GL}(n,F)$ modulo ${\ell }\not = p$, Invent. Math. 144 (2001), 177–223.CrossRefGoogle Scholar
Vignéras, M.-F., Irreducible modular representations of a reductive p-adic group and simple modules for Hecke algebras, in European Congress of Mathematics, Vol. I (Barcelona, 2000), Progress in Mathematics, vol. 201 (Birkhäuser, Basel, 2001), 117–133.Google Scholar
Zou, J., Supercuspidal representations of $\mathrm {GL}_{n}(F)$ distinguished by a unitary involution, Bull. Soc. Math. France 150 (2022), 393–458.Google Scholar