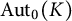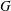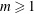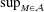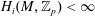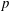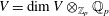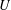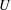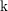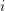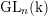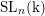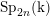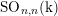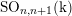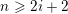Refine search
Actions for selected content:
31 results
On the homology stability range for symplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 11 December 2025, pp. 2724-2753
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher incoherence of the automorphism groups of a free group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for graphs of free groups with cyclic edge groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1576-1614
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher dimensional algebraic fiberings for pro-p groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 300-323
- Print publication:
- February 2025
-
- Article
- Export citation
FAITHFULNESS OF THE 2-BRAID GROUP VIA ZIGZAG ALGEBRA IN TYPE B
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 67-84
- Print publication:
- August 2024
-
- Article
- Export citation
On subdirect products of type FPn of limit groups over Droms RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 417-440
- Print publication:
- March 2024
-
- Article
- Export citation
Generalized Bockstein maps and Massey products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 January 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGICAL MACKEY 2-FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 August 2022, pp. 279-309
- Print publication:
- January 2024
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
Higher horospherical limit sets for G-modules over CAT(0)-spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 12 March 2021, pp. 133-163
- Print publication:
- July 2021
-
- Article
- Export citation
ON THE DIMENSION OF GROUPS THAT SATISFY CERTAIN CONDITIONS ON THEIR FINITE SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 November 2020, pp. 45-50
- Print publication:
- January 2022
-
- Article
- Export citation
On the Bieri–Neumann–Strebel–Renz invariants of residually free groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 807-829
-
- Article
- Export citation
Cohen–Lenstra heuristics for étale group schemes and symplectic pairings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 758-775
- Print publication:
- April 2019
-
- Article
- Export citation
Growth of Homology of Centre-by-metabelian Pro-
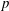 $p$ Groups
$p$ Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 203-224
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 May 2018, e6
-
- Article
-
- You have access
- Open access
- Export citation
Homological vanishing for the Steinberg representation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1111-1130
- Print publication:
- June 2018
-
- Article
- Export citation
A Note on Fine Graphs and Homological Isoperimetric Inequalities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-181
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
ON THE CAPABILITY OF FINITELY GENERATED NON-TORSION GROUPS OF NILPOTENCY CLASS 2
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 21 March 2011, pp. 411-417
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation