No CrossRef data available.
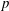 $p$ Groups
$p$ GroupsPublished online by Cambridge University Press: 09 January 2019
For a centre-by-metabelian pro-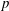 $p$ group
$p$ group 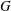 $G$ of type
$G$ of type 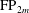 $\text{FP}_{2m}$, for some
$\text{FP}_{2m}$, for some 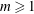 $m\geqslant 1$, we show that
$m\geqslant 1$, we show that 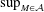 $\sup _{M\in {\mathcal{A}}}$ rk
$\sup _{M\in {\mathcal{A}}}$ rk 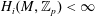 $H_{i}(M,\mathbb{Z}_{p})<\infty$, for all
$H_{i}(M,\mathbb{Z}_{p})<\infty$, for all 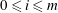 $0\leqslant i\leqslant m$, where
$0\leqslant i\leqslant m$, where 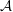 ${\mathcal{A}}$ is the set of all subgroups of
${\mathcal{A}}$ is the set of all subgroups of 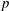 $p$-power index in
$p$-power index in 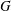 $G$ and, for a finitely generated abelian pro-
$G$ and, for a finitely generated abelian pro-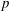 $p$ group
$p$ group 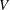 $V$, rk
$V$, rk 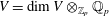 $V=\dim V\otimes _{\mathbb{Z}_{p}}\mathbb{Q}_{p}$.
$V=\dim V\otimes _{\mathbb{Z}_{p}}\mathbb{Q}_{p}$.
Author D. H. K. was partially supported by “bolsa de produtividade em pesquisa” 303350/2013-0 CNPq, Brazil and “projeto de pesquisa regular” FAPESP 2016/05678-3; author A. G. S. P. was partially supported by “Projeto Universal 482658/2013-4” from CNPq, Brazil.