Article contents
Cohen–Lenstra heuristics for étale group schemes and symplectic pairings
Published online by Cambridge University Press: 20 March 2019
Abstract
We generalize the Cohen–Lenstra heuristics over function fields to étale group schemes 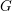 $G$ (with the classical case of abelian groups corresponding to constant group schemes). By using the results of Ellenberg–Venkatesh–Westerland, we make progress towards the proof of these heuristics. Moreover, by keeping track of the image of the Weil-pairing as an element of
$G$ (with the classical case of abelian groups corresponding to constant group schemes). By using the results of Ellenberg–Venkatesh–Westerland, we make progress towards the proof of these heuristics. Moreover, by keeping track of the image of the Weil-pairing as an element of 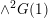 $\wedge ^{2}G(1)$, we formulate more refined heuristics which nicely explain the deviation from the usual Cohen–Lenstra heuristics for abelian
$\wedge ^{2}G(1)$, we formulate more refined heuristics which nicely explain the deviation from the usual Cohen–Lenstra heuristics for abelian 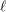 $\ell$-groups in cases where
$\ell$-groups in cases where 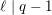 $\ell \mid q-1$; the nature of this failure was suggested already in the works of Malle, Garton, Ellenberg–Venkatesh–Westerland, and others. On the purely large random matrix side, we provide a natural model which has the correct moments, and we conjecture that these moments uniquely determine a limiting probability measure.
$\ell \mid q-1$; the nature of this failure was suggested already in the works of Malle, Garton, Ellenberg–Venkatesh–Westerland, and others. On the purely large random matrix side, we provide a natural model which has the correct moments, and we conjecture that these moments uniquely determine a limiting probability measure.
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
References
- 2
- Cited by

