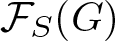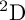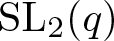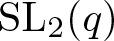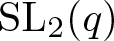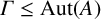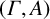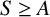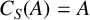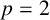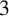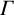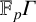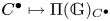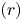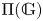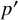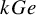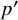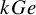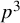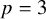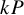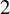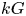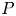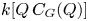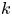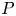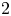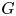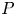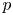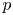Refine search
Actions for selected content:
75 results
Inductive local-global conditions and generalised Harish-Chandra theory
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 October 2025, e172
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-RATIONALITY OF HEIGHT-ZERO CHARACTERS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 14 August 2025, e7
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LARGEST CHARACTER DEGREE OF SOLVABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
$M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 May 2025, pp. 1-5
-
- Article
- Export citation
Conditions for the supersolvability of
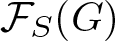 $\mathcal{F}_{S}(G)$
$\mathcal{F}_{S}(G)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 23 January 2025, pp. 566-572
-
- Article
- Export citation
A local-global principle for unipotent characters
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 December 2024, e125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS OF CHARACTERS IN TYPE D AND THE INDUCTIVE MCKAY CONDITION, I
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 906-958
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime divisors and the number of conjugacy classes of finite groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weights in a Benson-Solomon block
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trivial source character tables of
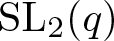 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 689-709
-
- Article
- Export citation
REAL BLOCKS WITH DIHEDRAL DEFECT GROUPS REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 14 June 2023, pp. 327-341
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONREALIZABILITY OF CERTAIN REPRESENTATIONS IN FUSION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 257-288
- Print publication:
- April 2024
-
- Article
- Export citation
Support varieties and stable categories for algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 27 March 2023, pp. 746-779
- Print publication:
- April 2023
-
- Article
- Export citation
Structure of blocks with normal defect and abelian
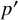 $p'$ inertial quotient
$p'$ inertial quotient
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 March 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON LARGE ORBITS OF FINITE SOLVABLE GROUPS ON CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 438-442
- Print publication:
- December 2023
-
- Article
- Export citation
Quasi-isolated blocks and the Alperin–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 June 2022, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HIGHER FROBENIUS–SCHUR INDICATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 12 July 2021, pp. 267-277
- Print publication:
- April 2022
-
- Article
- Export citation
On class 2 quotients of linear groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 09 June 2021, pp. 590-593
-
- Article
- Export citation
Brauer indecomposability of Scott modules with semidihedral vertex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 174-182
-
- Article
- Export citation