No CrossRef data available.
Article contents
Support varieties and stable categories for algebraic groups
Published online by Cambridge University Press: 27 March 2023
Abstract
We consider rational representations of a connected linear algebraic group 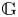 $\mathbb {G}$ over a field
$\mathbb {G}$ over a field 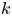 $k$ of positive characteristic
$k$ of positive characteristic 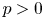 $p > 0$. We introduce a natural extension
$p > 0$. We introduce a natural extension 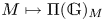 $M \mapsto \Pi (\mathbb {G})_M$ to
$M \mapsto \Pi (\mathbb {G})_M$ to 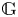 $\mathbb {G}$-modules of the
$\mathbb {G}$-modules of the 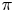 $\pi$-point support theory for modules
$\pi$-point support theory for modules 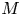 $M$ for a finite group scheme
$M$ for a finite group scheme 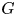 $G$ and show that this theory is essentially equivalent to the more ‘intrinsic’ and ‘explicit’ theory
$G$ and show that this theory is essentially equivalent to the more ‘intrinsic’ and ‘explicit’ theory 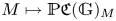 $M \mapsto \mathbb {P}\mathfrak{C}(\mathbb {G})_M$ of supports for an algebraic group of exponential type, a theory which uses
$M \mapsto \mathbb {P}\mathfrak{C}(\mathbb {G})_M$ of supports for an algebraic group of exponential type, a theory which uses 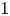 $1$-parameter subgroups
$1$-parameter subgroups 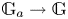 $\mathbb {G}_a \to \mathbb {G}$. We extend our support theory to bounded complexes of
$\mathbb {G}_a \to \mathbb {G}$. We extend our support theory to bounded complexes of  $\mathbb {G}$-modules,
$\mathbb {G}$-modules, 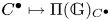 $C^\bullet \mapsto \Pi (\mathbb {G})_{C^\bullet }$. We introduce the tensor triangulated category
$C^\bullet \mapsto \Pi (\mathbb {G})_{C^\bullet }$. We introduce the tensor triangulated category 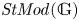 $\mathit {StMod}(\mathbb {G})$, the Verdier quotient of the bounded derived category
$\mathit {StMod}(\mathbb {G})$, the Verdier quotient of the bounded derived category 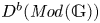 $D^b(\mathit {Mod}(\mathbb {G}))$ by the thick subcategory of mock injective modules. Our support theory satisfies all the ‘standard properties’ for a theory of supports for
$D^b(\mathit {Mod}(\mathbb {G}))$ by the thick subcategory of mock injective modules. Our support theory satisfies all the ‘standard properties’ for a theory of supports for 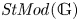 $\mathit {StMod}(\mathbb {G})$. As an application, we employ
$\mathit {StMod}(\mathbb {G})$. As an application, we employ 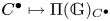 $C^\bullet \mapsto \Pi (\mathbb {G})_{C^\bullet }$ to establish the classification of
$C^\bullet \mapsto \Pi (\mathbb {G})_{C^\bullet }$ to establish the classification of 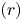 $(r)$-complete, thick tensor ideals of
$(r)$-complete, thick tensor ideals of 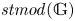 $\mathit {stmod}(\mathbb {G})$ in terms of locally
$\mathit {stmod}(\mathbb {G})$ in terms of locally 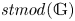 $\mathit {stmod}(\mathbb {G})$-realizable subsets of
$\mathit {stmod}(\mathbb {G})$-realizable subsets of 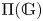 $\Pi (\mathbb {G})$ and the classification of
$\Pi (\mathbb {G})$ and the classification of 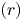 $(r)$-complete, localizing subcategories of
$(r)$-complete, localizing subcategories of 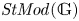 $\mathit {StMod}(\mathbb {G})$ in terms of locally
$\mathit {StMod}(\mathbb {G})$ in terms of locally 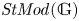 $\mathit {StMod}(\mathbb {G})$-realizable subsets of
$\mathit {StMod}(\mathbb {G})$-realizable subsets of 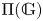 $\Pi (\mathbb {G})$.
$\Pi (\mathbb {G})$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
Dedicated to the memory of Brian Parshall
The author was partially supported by the Simons Foundation.


