No CrossRef data available.
Article contents
ON HIGHER FROBENIUS–SCHUR INDICATORS
Part of:
Representation theory of groups
Published online by Cambridge University Press: 12 July 2021
Abstract
Similarly to the Frobenius–Schur indicator of irreducible characters, we consider higher Frobenius–Schur indicators 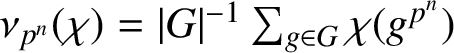 $\nu _{p^n}(\chi ) = |G|^{-1} \sum _{g \in G} \chi (g^{p^n})$ for primes p and
$\nu _{p^n}(\chi ) = |G|^{-1} \sum _{g \in G} \chi (g^{p^n})$ for primes p and 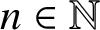 $n \in \mathbb {N}$, where G is a finite group and
$n \in \mathbb {N}$, where G is a finite group and 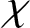 $\chi $ is a generalised character of G. These invariants give answers to interesting questions in representation theory. In particular, we give several characterisations of groups via higher Frobenius–Schur indicators.
$\chi $ is a generalised character of G. These invariants give answers to interesting questions in representation theory. In particular, we give several characterisations of groups via higher Frobenius–Schur indicators.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
Both authors were supported by NSFC (11661042 and 11761034) and the Natural Science Foundation of Jiangxi Province (20192ACB21008).
References
Chen, X., Cossey, J. P., Lewis, M. L. and Tong-Viet, H. P., ‘Blocks of small defect in alternating groups and squares of Brauer character degrees’, Group Theory 20 (2017), 1155–1173.Google Scholar
Gow, R., Huppert, B., Knörr, R., Manz, O. and Willems, W., Representation Theory in Arbitrary Characteristic, Casa Editrice Dott. Antonio Milani (CIRM,
Trento, 1993).Google Scholar
Gow, R. and Willems, W., ‘Quadratic geometries, projective modules, and idempotents’, J. Algebra 160 (1993), 257–272.10.1006/jabr.1993.1187CrossRefGoogle Scholar
Granville, A. and Ono, K., ‘Defect zero
 $p$
-blocks for finite simple groups’, Trans. Amer. Math. Soc. 348 (1996), 331–347.10.1090/S0002-9947-96-01481-XCrossRefGoogle Scholar
$p$
-blocks for finite simple groups’, Trans. Amer. Math. Soc. 348 (1996), 331–347.10.1090/S0002-9947-96-01481-XCrossRefGoogle Scholar
Huppert, B., Endliche Gruppen (Springer,
Berlin–Heidelberg–New York, 1967).10.1007/978-3-642-64981-3CrossRefGoogle Scholar
Liu, X., Wang, Y. and Wei, H., ‘Notes on the conjugacy classes of finite groups’, J. Pure Appl. Algebra 196 (2005), 111–117.10.1016/j.jpaa.2004.08.020CrossRefGoogle Scholar
Martínez-Pérez, C. and Willems, W., ‘Involutions, cohomology and metabolic spaces’, J. Algebra 327 (2011), 4445–4451.10.1016/j.jalgebra.2010.07.002CrossRefGoogle Scholar
Michler, G. O., ‘A finite simple group of Lie type has
 $p$
-blocks of different defects,
$p$
-blocks of different defects,
 $p\ne 2$
’, J. Algebra 104 (1986), 220–230.10.1016/0021-8693(86)90212-7CrossRefGoogle Scholar
$p\ne 2$
’, J. Algebra 104 (1986), 220–230.10.1016/0021-8693(86)90212-7CrossRefGoogle Scholar
Murray, J., ‘Strongly real
 $2$
-blocks and the Frobenius–Schur indicator’, Osaka J. Math. 43 (2006), 201–213.Google Scholar
$2$
-blocks and the Frobenius–Schur indicator’, Osaka J. Math. 43 (2006), 201–213.Google Scholar
Murray, J., ‘Projective modules and involutions’, J. Algebra 299 (2006), 616–622.10.1016/j.jalgebra.2005.05.032CrossRefGoogle Scholar
Murray, J., ‘Projective indecomposable modules, Scott modules and the Frobenius–Schur indicator’, J. Algebra 311(2) (2007), 800–816.10.1016/j.jalgebra.2006.12.009CrossRefGoogle Scholar
Murray, J., ‘Components of the involution module in blocks with a cyclic or Klein-four defect group’, J. Group Theory 11(1) (2008), 43–62.10.1515/JGT.2008.003CrossRefGoogle Scholar
Navarro, G., Characters and Blocks of Finite Groups, London Mathematical Society Lecture Note Series, 250 (Cambridge University Press,
Cambridge, 1998).10.1017/CBO9780511526015CrossRefGoogle Scholar
Quillen, D., ‘The Adams conjecture’, Topology 10 (1970), 67–80.10.1016/0040-9383(71)90018-8CrossRefGoogle Scholar
Ren, Y., ‘On the
 $p$
-length of
$p$
-length of
 $p$
-regular classes and the
$p$
-regular classes and the
 $p$
-structure of finite groups’, Algebra Colloq. 2 (1995), 3–10.Google Scholar
$p$
-structure of finite groups’, Algebra Colloq. 2 (1995), 3–10.Google Scholar
Robinson, G. R., ‘The Frobenius–Schur indicator and projective modules’, J. Algebra 126 (1989), 252–257.10.1016/0021-8693(89)90331-1CrossRefGoogle Scholar
Thompson, J. G., ‘Finite groups which appear as Gal
 $L/K$
, where
$L/K$
, where
 $K\subseteq Q\left({\mu}_n\right)$
’, in: Group Theory, Beijing 1984 (ed. Hsio-Fu, T.), Lecture Notes in Mathematics, 1185 (Springer,
Berlin, 1986), 210–230.10.1007/BFb0076176CrossRefGoogle Scholar
$K\subseteq Q\left({\mu}_n\right)$
’, in: Group Theory, Beijing 1984 (ed. Hsio-Fu, T.), Lecture Notes in Mathematics, 1185 (Springer,
Berlin, 1986), 210–230.10.1007/BFb0076176CrossRefGoogle Scholar
Tsushima, Y., ‘On the weakly regular
 $p$
-blocks with respect to
$p$
-blocks with respect to
 ${O}_{p^{\prime }}(G)$
’, Osaka J.Math. 14 (1977), 465–470.Google Scholar
${O}_{p^{\prime }}(G)$
’, Osaka J.Math. 14 (1977), 465–470.Google Scholar
Willems, W., Metrische Moduln über Gruppenringen, Thesis, Johannes Gutenberg Universität,
Mainz, 1976.Google Scholar
Willems, W., ‘Gruppen, deren nichtlineare Charaktere von symplektischen Typ sind’, Arch. Math. (Basel) 29 (1977), 383–384.10.1007/BF01220422CrossRefGoogle Scholar
Willems, W., ‘Duality and forms in representation theory’, in: Representation Theory of Finite Groups and Finite-dimensional Algebras (Birkhäuser,
Basel, 1991), 509–520.10.1007/978-3-0348-8658-1_24CrossRefGoogle Scholar


