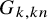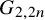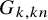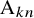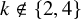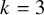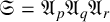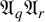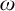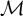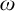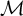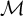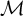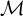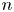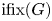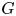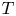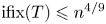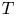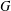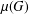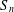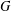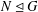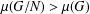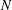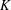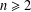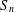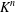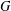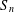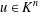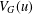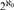12 results
A complete classification of shuffle groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 04 December 2024, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENUMERATION OF GROUPS IN SOME SPECIAL VARIETIES OF A-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 107-117
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
CLASSIFICATION OF
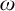 $\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
$\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 460-495
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the involution fixity of simple groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 408-426
-
- Article
- Export citation
SUBGROUPS WITH NO ABELIAN COMPOSITION FACTORS ARE NOT DISTINGUISHED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 446-452
- Print publication:
- June 2020
-
- Article
- Export citation
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 April 2019, pp. 256-267
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
THE COMPLEXITY OF TOPOLOGICAL GROUP ISOMORPHISM
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 1190-1203
- Print publication:
- September 2018
-
- Article
- Export citation
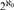 ${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS
${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 395-415
- Print publication:
- June 2018
-
- Article
- Export citation
UNIVERSAL SUBGROUPS OF POLISH GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 12 December 2014, pp. 1148-1183
- Print publication:
- December 2014
-
- Article
- Export citation
EMBEDDING PERMUTATION GROUPS INTO WREATH PRODUCTS IN PRODUCT ACTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 24 April 2012, pp. 127-136
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Transitive simple subgroups of wreath products in product action
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-72
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation