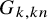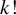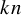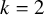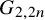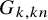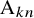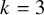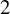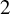1 Introduction
For a deck of
![]() $2n$
cards, the usual way to perfectly shuffle the deck is to first cut the deck in half (see Figure 1) and then perfectly interleave the two halves. There are two kinds of such shuffles according to whether the original top card remains on top or not (see Figures 2 and 3). Note that these two shuffles are permutations of the
$2n$
cards, the usual way to perfectly shuffle the deck is to first cut the deck in half (see Figure 1) and then perfectly interleave the two halves. There are two kinds of such shuffles according to whether the original top card remains on top or not (see Figures 2 and 3). Note that these two shuffles are permutations of the
![]() $2n$
cards. To exactly know what permutations of the cards can be achieved by performing a sequence of these two shuffles, one needs to determine the permutation group generated by these two shuffles. In 1983, Diaconis, Graham and Kantor [Reference Diaconis, Graham and Kantor8] completely determined this group for all n (see Theorem 1.1). Moreover, at the end of [Reference Diaconis, Graham and Kantor8], they suggested a more general problem: For an integer
$2n$
cards. To exactly know what permutations of the cards can be achieved by performing a sequence of these two shuffles, one needs to determine the permutation group generated by these two shuffles. In 1983, Diaconis, Graham and Kantor [Reference Diaconis, Graham and Kantor8] completely determined this group for all n (see Theorem 1.1). Moreover, at the end of [Reference Diaconis, Graham and Kantor8], they suggested a more general problem: For an integer
![]() $k\geq 2$
, if a deck of
$k\geq 2$
, if a deck of
![]() $kn$
cards are divided into k piles with n cards in each pile, then there are
$kn$
cards are divided into k piles with n cards in each pile, then there are
![]() $k!$
possible orders of picking up the piles to perfectly interleave. Therefore, there are
$k!$
possible orders of picking up the piles to perfectly interleave. Therefore, there are
![]() $k!$
such ways to perfectly shuffle the
$k!$
such ways to perfectly shuffle the
![]() $kn$
cards, and one may consider the group generated by these
$kn$
cards, and one may consider the group generated by these
![]() $k!$
permutations.
$k!$
permutations.

Figure 1 Cut the deck.

Figure 2 Out-shuffle.

Figure 3 In-shuffle.
Throughout this paper, for a positive integer m, we set
For a deck of
![]() $kn$
cards, the card in position
$kn$
cards, the card in position
![]() $i+jn$
, where
$i+jn$
, where
![]() $i\in [n]$
and
$i\in [n]$
and
![]() $j\in [k]$
, refers to the
$j\in [k]$
, refers to the
![]() $(i+jn)$
-th card from top to bottom with the top one being the
$(i+jn)$
-th card from top to bottom with the top one being the
![]() $0$
-th card. We may also think of them in k piles such that the j-th pile consists of the cards in the positions
$0$
-th card. We may also think of them in k piles such that the j-th pile consists of the cards in the positions
![]() $jn,1+jn,\dots ,n-1+jn$
, where
$jn,1+jn,\dots ,n-1+jn$
, where
![]() $j\in \{0,1,\dots ,k-1\}$
. The standard shuffle of the
$j\in \{0,1,\dots ,k-1\}$
. The standard shuffle of the
![]() $kn$
cards, denoted by
$kn$
cards, denoted by
![]() $\sigma $
, is performed by picking up the top card from each of the piles
$\sigma $
, is performed by picking up the top card from each of the piles
![]() $0,\dots ,k-1$
in order and repeating until all cards have been picked up; that is,
$0,\dots ,k-1$
in order and repeating until all cards have been picked up; that is,
![]() $\sigma $
is the permutation of
$\sigma $
is the permutation of
![]() $[kn]$
defined by
$[kn]$
defined by
Let
![]() $\tau \in \mathrm {Sym}([k])$
be a permutation of the k piles. Then
$\tau \in \mathrm {Sym}([k])$
be a permutation of the k piles. Then
![]() $\tau $
induces a permutation
$\tau $
induces a permutation
![]() $\rho _\tau $
of the
$\rho _\tau $
of the
![]() $kn$
cards by keeping the order of the cards within each pile, so that
$kn$
cards by keeping the order of the cards within each pile, so that
The card shuffle
![]() $\rho _\tau \sigma $
is to first perform
$\rho _\tau \sigma $
is to first perform
![]() $\rho _\tau $
and then
$\rho _\tau $
and then
![]() $\sigma $
; that is,
$\sigma $
; that is,
The subgroup of
![]() $\mathrm {Sym}([kn])$
generated by
$\mathrm {Sym}([kn])$
generated by
![]() $\rho _\tau \sigma $
for all
$\rho _\tau \sigma $
for all
![]() $\tau \in \mathrm {Sym}([k])$
is called the shuffle group on
$\tau \in \mathrm {Sym}([k])$
is called the shuffle group on
![]() $kn$
cards and denoted by
$kn$
cards and denoted by
![]() $G_{k,kn}$
; that is,
$G_{k,kn}$
; that is,
In this terminology, what is suggested at the end of [Reference Diaconis, Graham and Kantor8] is to determine the shuffle group
![]() $G_{k,kn}$
.
$G_{k,kn}$
.
For a positive integer m, let
![]() $C_m$
,
$C_m$
,
![]() $A_m$
and
$A_m$
and
![]() $S_m$
be the cyclic group of order m, alternating group on m points and symmetric group on m points, respectively. In 1983, Diaconis, Graham and Kantor [Reference Diaconis, Graham and Kantor8] completely determined
$S_m$
be the cyclic group of order m, alternating group on m points and symmetric group on m points, respectively. In 1983, Diaconis, Graham and Kantor [Reference Diaconis, Graham and Kantor8] completely determined
![]() $G_{2,2n}$
as follows.
$G_{2,2n}$
as follows.
Theorem 1.1 (Diaconis-Graham-Kantor).
For
![]() $G=G_{2,2n}$
, the following hold:
$G=G_{2,2n}$
, the following hold:
-
(a) If
 $n\equiv 0\ \pmod {4}$
,
$n\equiv 0\ \pmod {4}$
,
 $n>12$
and n is not a power of
$n>12$
and n is not a power of
 $2$
, then
$2$
, then
 $G=C^{n-1}_2\rtimes A_n$
.
$G=C^{n-1}_2\rtimes A_n$
. -
(b) If
 $n\equiv 1\ \pmod {4}$
, then
$n\equiv 1\ \pmod {4}$
, then
 $G=C^n_2\rtimes A_n$
.
$G=C^n_2\rtimes A_n$
. -
(c) If
 $n\equiv 2\ \pmod {4}$
and
$n\equiv 2\ \pmod {4}$
and
 $n>6$
, then G is the imprimitive wreath product
$n>6$
, then G is the imprimitive wreath product
 $C_2\wr S_n$
.
$C_2\wr S_n$
. -
(d) If
 $n\equiv 3\ \pmod {4}$
, then
$n\equiv 3\ \pmod {4}$
, then
 $G=C^{n-1}_2\rtimes S_n$
is the Weyl group of the root system
$G=C^{n-1}_2\rtimes S_n$
is the Weyl group of the root system
 $D_n$
.
$D_n$
. -
(e) If
 $n=2^m$
for some positive integer m, then G is the primitive wreath product
$n=2^m$
for some positive integer m, then G is the primitive wreath product
 $C_2\wr C_{m+1}$
.
$C_2\wr C_{m+1}$
. -
(f) If
 $n=6$
, then
$n=6$
, then
 $G=C_2^6\rtimes \mathrm {PGL}(2,5)$
.
$G=C_2^6\rtimes \mathrm {PGL}(2,5)$
. -
(g) If
 $n=12$
, then
$n=12$
, then
 $G=C_2^{11}\rtimes M_{12}$
, where
$G=C_2^{11}\rtimes M_{12}$
, where
 $M_{12}$
is the Mathieu group on
$M_{12}$
is the Mathieu group on
 $12$
points.
$12$
points.
In 1987, Medvedoff and Morrison [Reference Medvedoff and Morrison13] initiated a systematic study of the shuffle group
![]() $G_{k,kn}$
for general k. They showed (see [Reference Medvedoff and Morrison13, Theorem 2]) that, if n is a power of k, then
$G_{k,kn}$
for general k. They showed (see [Reference Medvedoff and Morrison13, Theorem 2]) that, if n is a power of k, then
![]() $G_{k,kn}$
is the primitive wreath product of
$G_{k,kn}$
is the primitive wreath product of
![]() $S_k$
by the cyclic group of order
$S_k$
by the cyclic group of order
![]() $\log _k(kn)$
; that is,
$\log _k(kn)$
; that is,
Moreover, based on computation results, Medvedoff and Morrison conjectured in [Reference Medvedoff and Morrison13] that
![]() $G_{3,3n}$
contains
$G_{3,3n}$
contains
![]() $A_{3n}$
if n is not a power of
$A_{3n}$
if n is not a power of
![]() $3$
, which is essentially a conjectural classification of
$3$
, which is essentially a conjectural classification of
![]() $G_{3,3n}$
(see the Remark after Conjecture 1.2). Similarly, they made a conjecture for
$G_{3,3n}$
(see the Remark after Conjecture 1.2). Similarly, they made a conjecture for
![]() $k=4$
in the same paper, which states that
$k=4$
in the same paper, which states that
![]() $G_{4,4n}$
contains
$G_{4,4n}$
contains
![]() $A_{4n}$
if n is not a power of
$A_{4n}$
if n is not a power of
![]() $2$
, and
$2$
, and
![]() $G_{4,4n}$
is the full affine group of degree
$G_{4,4n}$
is the full affine group of degree
![]() $4n$
if n is an odd power of
$4n$
if n is an odd power of
![]() $2$
. The latter part of this conjecture, that is,
$2$
. The latter part of this conjecture, that is,
was confirmed in 2005 by Cohen, Harmse, Morrison and Wright [Reference Cohen, Harmse, Morrison and Wright7, Theorem 2.6]. This leads them to the following conjecture.
Conjecture 1.2 (Shuffle Group Conjecture).
For
![]() $k\geq 3$
, if n is not a power of k and
$k\geq 3$
, if n is not a power of k and
![]() $(k,n)\neq (4,2^f)$
for any positive integer f, then
$(k,n)\neq (4,2^f)$
for any positive integer f, then
![]() $G_{k,kn}$
contains
$G_{k,kn}$
contains
![]() $A_{kn}$
.
$A_{kn}$
.
Remark. From the definitions of
![]() $\sigma $
and
$\sigma $
and
![]() $\rho _\tau $
, it is not hard to see that
$\rho _\tau $
, it is not hard to see that
![]() $G_{k,kn}$
is a subgroup of
$G_{k,kn}$
is a subgroup of
![]() $A_{kn}$
if and only if either
$A_{kn}$
if and only if either
![]() $n\equiv 2\ \pmod 4$
and
$n\equiv 2\ \pmod 4$
and
![]() $k\equiv 0$
or
$k\equiv 0$
or
![]() $1\ \pmod 4$
, or
$1\ \pmod 4$
, or
![]() $n\equiv 0\ \pmod 4$
(see, for example, [Reference Medvedoff and Morrison13, Theorem 1]). This implies that
$n\equiv 0\ \pmod 4$
(see, for example, [Reference Medvedoff and Morrison13, Theorem 1]). This implies that
![]() $G_{k,kn}$
is precisely determined if we know that
$G_{k,kn}$
is precisely determined if we know that
![]() $G_{k,kn}$
contains
$G_{k,kn}$
contains
![]() $A_{kn}$
. Therefore, the above Shuffle Group Conjecture is in fact a conjectural classification of the shuffle groups
$A_{kn}$
. Therefore, the above Shuffle Group Conjecture is in fact a conjectural classification of the shuffle groups
![]() $G_{k,kn}$
for all
$G_{k,kn}$
for all
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n\geq 1$
.
$n\geq 1$
.
Among other results, Amarra, Morgan and Praeger [Reference Amarra, Morgan and Praeger1] recently confirmed Conjecture 1.2 for the following three cases:
-
(i)
 $k>n$
;
$k>n$
; -
(ii) k and n are powers of the same integer
 $\ell \geq 2$
;
$\ell \geq 2$
; -
(iii) k is a power of
 $2$
, and n is not a power of
$2$
, and n is not a power of
 $2$
.
$2$
.
Note that (ii) and (iii) together imply the validity of Conjecture 1.2 whenever k is a power of
![]() $2$
. We also remark that the Classification of Finite Simple Groups (CFSG) comes into play in the study of shuffle groups in [Reference Amarra, Morgan and Praeger1]. In fact, CFSG was already applied in an unpublished result of William Kantor (see [Reference Kantor11] and [Reference Medvedoff and Morrison13, Page 13]) to prove that
$2$
. We also remark that the Classification of Finite Simple Groups (CFSG) comes into play in the study of shuffle groups in [Reference Amarra, Morgan and Praeger1]. In fact, CFSG was already applied in an unpublished result of William Kantor (see [Reference Kantor11] and [Reference Medvedoff and Morrison13, Page 13]) to prove that
![]() $G_{k,kn}\geq A_{kn}$
if
$G_{k,kn}\geq A_{kn}$
if
![]() $k\geq 4$
and k does not divide n.
$k\geq 4$
and k does not divide n.
In this paper, we prove Conjecture 1.2 for all k and n (see Theorems 1.3 and 1.4). Our approach is to reduce the proof of the conjecture to that of the
![]() $2$
-transitivity of
$2$
-transitivity of
![]() $G_{k,kn}$
by considering the fixed point ratio of certain element therein. This approach makes use of some deep classification results (depending on CFSG) in group theory – for example, the classification of
$G_{k,kn}$
by considering the fixed point ratio of certain element therein. This approach makes use of some deep classification results (depending on CFSG) in group theory – for example, the classification of
![]() $2$
-transitive groups and primitive groups with elements of large fixed point ratio [Reference Burness4, Reference Guralnick and Magaard10, Reference Liebeck and Saxl12]. Our reduction theorem is as follows.
$2$
-transitive groups and primitive groups with elements of large fixed point ratio [Reference Burness4, Reference Guralnick and Magaard10, Reference Liebeck and Saxl12]. Our reduction theorem is as follows.
Theorem 1.3. If
![]() $G_{k,kn}$
is
$G_{k,kn}$
is
![]() $2$
-transitive with
$2$
-transitive with
![]() $k\geq 3$
, then either
$k\geq 3$
, then either
![]() $k=4$
and n is an odd power of
$k=4$
and n is an odd power of
![]() $2$
, or
$2$
, or
![]() $G_{k,kn}$
contains
$G_{k,kn}$
contains
![]() $A_{kn}$
.
$A_{kn}$
.
By Theorem 1.3, we can determine
![]() $G_{k,kn}$
for
$G_{k,kn}$
for
![]() $k\geq 3$
if it is shown to be
$k\geq 3$
if it is shown to be
![]() $2$
-transitive. This is the case when n is not a power of k, as the following theorem states.
$2$
-transitive. This is the case when n is not a power of k, as the following theorem states.
Theorem 1.4. The shuffle group
![]() $G_{k,kn}$
is
$G_{k,kn}$
is
![]() $2$
-transitive if
$2$
-transitive if
![]() $k\geq 3$
and n is not a power of k.
$k\geq 3$
and n is not a power of k.
The combination of Theorems 1.3 and 1.4 completely solves Conjecture 1.2 affirmatively. Now that Conjecture 1.2 is confirmed, it together with [Reference Medvedoff and Morrison13, Theorem 2] and [Reference Cohen, Harmse, Morrison and Wright7, Theorem 2.6] leads to (see the remark after Conjecture 1.2) the following complete classification of shuffle groups.
Theorem 1.5. If
![]() $k\geq 3$
, then the following hold:
$k\geq 3$
, then the following hold:
-
(a) If
 $kn=k^m$
, then
$kn=k^m$
, then
 $G_{k,kn}$
is the primitive wreath product
$G_{k,kn}$
is the primitive wreath product
 $S_k\wr C_m$
.
$S_k\wr C_m$
. -
(b) If
 $k=4$
and
$k=4$
and
 $kn=2^m$
with m odd, then
$kn=2^m$
with m odd, then
 $G_{k,kn}$
is the affine group
$G_{k,kn}$
is the affine group
 $\mathrm {AGL}(m,2)$
.
$\mathrm {AGL}(m,2)$
. -
(c) If n is not a power of k and either n is odd or both
 $n/2$
and
$n/2$
and
 $k(k-1)/2$
are odd integers, then
$k(k-1)/2$
are odd integers, then
 $G_{k,kn}=S_{kn}$
.
$G_{k,kn}=S_{kn}$
. -
(d) In all other cases,
 $G_{k,kn}=A_{kn}$
.
$G_{k,kn}=A_{kn}$
.
The remainder of this paper is structured as follows. In the next section, we will give definitions and some technical lemmas that will be used in Section 3. After this preparation, Theorem 1.3 will be proved in Section 3, and the proof of Theorems 1.4 will be given in Section 4. Finally, in Section 5, we conclude the paper with some open problems on the so-called generalised shuffle groups introduced by Amarra, Morgan and Praeger [Reference Amarra, Morgan and Praeger1].
2 Preliminaries
For a finite group G, let
![]() $\mathbf {Z}(G)$
denote the centre of G, let
$\mathbf {Z}(G)$
denote the centre of G, let
![]() $\mathbf {O}_p(G)$
denote the largest normal p-subgroup of G for a prime p, and let
$\mathbf {O}_p(G)$
denote the largest normal p-subgroup of G for a prime p, and let
![]() $\mathbf {C}_G(g)$
denote the centraliser of an element g in G. The socle of G is the product of the minimal normal subgroups of G, denoted by
$\mathbf {C}_G(g)$
denote the centraliser of an element g in G. The socle of G is the product of the minimal normal subgroups of G, denoted by
![]() $\mathrm {Soc}(G)$
. The fixed point ratio of a permutation g on a finite set
$\mathrm {Soc}(G)$
. The fixed point ratio of a permutation g on a finite set
![]() $\Omega $
, denoted by
$\Omega $
, denoted by
![]() $\mathrm {fpr}(g)$
, is defined by
$\mathrm {fpr}(g)$
, is defined by
where
![]() $\mathrm {Fix}(g)=\{\alpha \in \Omega \mid \alpha ^g=\alpha \}$
.
$\mathrm {Fix}(g)=\{\alpha \in \Omega \mid \alpha ^g=\alpha \}$
.
Lemma 2.1. Let g be an element of
![]() $\mathrm {PGL}(d,3)$
acting on the set of
$\mathrm {PGL}(d,3)$
acting on the set of
![]() $1$
-dimensional subspaces of the vector space
$1$
-dimensional subspaces of the vector space
![]() $\mathbb {F}_3^d$
. Then
$\mathbb {F}_3^d$
. Then
for some nonnegative integers s and t.
Proof. Let
![]() $\hat {g}\in \mathrm {GL}(d,3)$
such that
$\hat {g}\in \mathrm {GL}(d,3)$
such that
![]() $g=\hat {g}\mathbf {Z}(\mathrm {GL}(d,3))\in \mathrm {PGL}(d,3)$
. Note that a
$g=\hat {g}\mathbf {Z}(\mathrm {GL}(d,3))\in \mathrm {PGL}(d,3)$
. Note that a
![]() $1$
-dimensional subspace
$1$
-dimensional subspace
![]() $\langle v\rangle $
of
$\langle v\rangle $
of
![]() $\mathbb {F}^d_3$
satisfies
$\mathbb {F}^d_3$
satisfies
![]() $\langle v\rangle ^g=\langle v\rangle $
if and only if
$\langle v\rangle ^g=\langle v\rangle $
if and only if
![]() $v^{\hat {g}}$
is v or
$v^{\hat {g}}$
is v or
![]() $-v$
. Therefore,
$-v$
. Therefore,
and hence,
 $$\begin{align*}\mathrm{fpr}(g)=\frac{|\mathrm{Fix}(g)|}{|\{\langle v\rangle\mid v\in\mathbb{F}^d_3\setminus\{0\}\}|}=\frac{\frac{3^s-1}{2}+\frac{3^t-1}{2}}{\frac{3^d-1}{2}}=\frac{3^s+3^t-2}{3^d-1}, \end{align*}$$
$$\begin{align*}\mathrm{fpr}(g)=\frac{|\mathrm{Fix}(g)|}{|\{\langle v\rangle\mid v\in\mathbb{F}^d_3\setminus\{0\}\}|}=\frac{\frac{3^s-1}{2}+\frac{3^t-1}{2}}{\frac{3^d-1}{2}}=\frac{3^s+3^t-2}{3^d-1}, \end{align*}$$
where s and t are the dimensions of the
![]() $1$
-eigenspace and (
$1$
-eigenspace and (
![]() $-1$
)-eigenspace of
$-1$
)-eigenspace of
![]() $\hat {g}$
, respectively.
$\hat {g}$
, respectively.
Let
![]() $V=\mathbb {F}_q^d$
be a d-dimensional vector space over
$V=\mathbb {F}_q^d$
be a d-dimensional vector space over
![]() $\mathbb {F}_q$
, where
$\mathbb {F}_q$
, where
![]() $d\geq 3$
and q is even, and we fix an ordered basis of V and associate each element of
$d\geq 3$
and q is even, and we fix an ordered basis of V and associate each element of
![]() $\mathrm {SL}(V)$
with its matrix under this basis. For an involution
$\mathrm {SL}(V)$
with its matrix under this basis. For an involution
![]() $g\in \mathrm {SL}(V)$
, denote by
$g\in \mathrm {SL}(V)$
, denote by
![]() $r(g)$
the number of Jordan blocks of size
$r(g)$
the number of Jordan blocks of size
![]() $2$
in the Jordan canonical form of g. Note that two involutions A and B in
$2$
in the Jordan canonical form of g. Note that two involutions A and B in
![]() $\mathrm {SL}(V)$
are conjugate in
$\mathrm {SL}(V)$
are conjugate in
![]() $\mathrm {SL}(V)$
if and only if
$\mathrm {SL}(V)$
if and only if
![]() $r(A)=r(B)$
. For an integer
$r(A)=r(B)$
. For an integer
![]() $\ell $
with
$\ell $
with
![]() $1\leq \ell \leq d/2$
, denote
$1\leq \ell \leq d/2$
, denote
 $$\begin{align*}A_\ell=\begin{pmatrix}I_\ell & & \\ & I_{d-2\ell} & \\ I_\ell & & I_\ell\end{pmatrix}, \end{align*}$$
$$\begin{align*}A_\ell=\begin{pmatrix}I_\ell & & \\ & I_{d-2\ell} & \\ I_\ell & & I_\ell\end{pmatrix}, \end{align*}$$
where
![]() $I_j$
is the
$I_j$
is the
![]() $j\times j$
identity matrix. It is clear that
$j\times j$
identity matrix. It is clear that
![]() $A_\ell $
is an involution in
$A_\ell $
is an involution in
![]() $\mathrm {SL}(V)$
with
$\mathrm {SL}(V)$
with
![]() $r(A_\ell )=\ell $
. We call
$r(A_\ell )=\ell $
. We call
![]() $A_\ell $
the Suzuki form of the conjugacy class of
$A_\ell $
the Suzuki form of the conjugacy class of
![]() $A_\ell $
in
$A_\ell $
in
![]() $\mathrm {SL}(V)$
.
$\mathrm {SL}(V)$
.
For
![]() $\varepsilon \in \{+,-\}$
, let
$\varepsilon \in \{+,-\}$
, let
![]() $\mathrm {O}^{\varepsilon }(2m,q)$
be the general orthogonal group of
$\mathrm {O}^{\varepsilon }(2m,q)$
be the general orthogonal group of
![]() $\varepsilon $
type on the space
$\varepsilon $
type on the space
![]() $\mathbb {F}_q^{2m}$
, where m is a positive integer and q is a prime power. For convenience, we set the notation
$\mathbb {F}_q^{2m}$
, where m is a positive integer and q is a prime power. For convenience, we set the notation
![]() $\mathrm {Sp}(0,q)$
and
$\mathrm {Sp}(0,q)$
and
![]() $\mathrm {O}^{\varepsilon }(0,q)$
to be the trivial group. The following lemma is a consequence of [Reference Aschbacher and Seitz2, Sections 7 and 8].
$\mathrm {O}^{\varepsilon }(0,q)$
to be the trivial group. The following lemma is a consequence of [Reference Aschbacher and Seitz2, Sections 7 and 8].
Lemma 2.2. For each involution
![]() $g\in \mathrm {O}^{\varepsilon }(2m,2)<\mathrm {Sp}(2m,2)$
, we have
$g\in \mathrm {O}^{\varepsilon }(2m,2)<\mathrm {Sp}(2m,2)$
, we have
 $$\begin{align*}\frac{|\mathbf{C}_{\mathrm{Sp}(2m,2)}(g)|}{|\mathbf{C}_{\mathrm{O}^{\varepsilon}(2m,2)}(g)|} =\frac{|\mathrm{Sp}(2m-2r,2)|\cdot|\mathbf{O}_2\left(\mathbf{C}_{\mathrm{Sp}(2m,2)}(g)\right)|} {|\mathrm{O}^{\varepsilon}(2m-2r,2)|\cdot|\mathbf{O}_2\left(\mathbf{C}_{\mathrm{O}^{\varepsilon}(2m,2)}(g)\right)|} \end{align*}$$
$$\begin{align*}\frac{|\mathbf{C}_{\mathrm{Sp}(2m,2)}(g)|}{|\mathbf{C}_{\mathrm{O}^{\varepsilon}(2m,2)}(g)|} =\frac{|\mathrm{Sp}(2m-2r,2)|\cdot|\mathbf{O}_2\left(\mathbf{C}_{\mathrm{Sp}(2m,2)}(g)\right)|} {|\mathrm{O}^{\varepsilon}(2m-2r,2)|\cdot|\mathbf{O}_2\left(\mathbf{C}_{\mathrm{O}^{\varepsilon}(2m,2)}(g)\right)|} \end{align*}$$
for some positive integer
![]() $r\leq m$
.
$r\leq m$
.
Proof. Write
![]() $G=\mathrm {Sp}(2m,2)$
and
$G=\mathrm {Sp}(2m,2)$
and
![]() $H=\mathrm {O}^{\varepsilon }(2m,2)$
. Since
$H=\mathrm {O}^{\varepsilon }(2m,2)$
. Since
![]() $g\in G$
, we see that there exists a basis of
$g\in G$
, we see that there exists a basis of
![]() $\mathbb {F}^{2m}_2$
as in (1), (2) or (3) of [Reference Aschbacher and Seitz2, (7.6)] such that g is in Suzuki form under this basis. For convenience, we say that g has form
$\mathbb {F}^{2m}_2$
as in (1), (2) or (3) of [Reference Aschbacher and Seitz2, (7.6)] such that g is in Suzuki form under this basis. For convenience, we say that g has form
![]() $a_\ell $
,
$a_\ell $
,
![]() $b_\ell $
or
$b_\ell $
or
![]() $c_\ell $
, if the basis is chosen as in (1), (2) or (3) of [Reference Aschbacher and Seitz2, (7.6)], respectively.
$c_\ell $
, if the basis is chosen as in (1), (2) or (3) of [Reference Aschbacher and Seitz2, (7.6)], respectively.
First assume that g has form
![]() $a_\ell $
(in this case,
$a_\ell $
(in this case,
![]() $\ell $
is even). It follows from [Reference Aschbacher and Seitz2, (7.9)] that there exists a homomorphism from
$\ell $
is even). It follows from [Reference Aschbacher and Seitz2, (7.9)] that there exists a homomorphism from
![]() $\mathbf {C}_G(g)$
onto
$\mathbf {C}_G(g)$
onto
![]() $\mathrm {Sp}(\ell ,2)\times \mathrm {Sp}(2m-2\ell ,2)$
with kernel
$\mathrm {Sp}(\ell ,2)\times \mathrm {Sp}(2m-2\ell ,2)$
with kernel
![]() $\mathbf {O}_2\left (\mathbf {C}_{G}(g)\right )$
. Therefore,
$\mathbf {O}_2\left (\mathbf {C}_{G}(g)\right )$
. Therefore,
Moreover, [Reference Aschbacher and Seitz2, (8.6)] shows that there is a homomorphism from
![]() $\mathbf {C}_{H}(g)$
to
$\mathbf {C}_{H}(g)$
to
![]() $\mathrm {Sp}(\ell ,2)\times \mathrm {O}^{\varepsilon }(2m-2\ell ,2)$
with kernel
$\mathrm {Sp}(\ell ,2)\times \mathrm {O}^{\varepsilon }(2m-2\ell ,2)$
with kernel
![]() $\mathbf {O}_2\left (\mathbf {C}_{H}(g)\right )$
, and so
$\mathbf {O}_2\left (\mathbf {C}_{H}(g)\right )$
, and so
As a consequence,
Now assume that g has form
![]() $b_\ell $
or
$b_\ell $
or
![]() $c_\ell $
(in this case,
$c_\ell $
(in this case,
![]() $\ell $
is odd or even, respectively). Similarly, we derive from [Reference Aschbacher and Seitz2, (7.10) and (7.11)] and [Reference Aschbacher and Seitz2, (8.7) and (8.8)] that
$\ell $
is odd or even, respectively). Similarly, we derive from [Reference Aschbacher and Seitz2, (7.10) and (7.11)] and [Reference Aschbacher and Seitz2, (8.7) and (8.8)] that
or
It follows that
This completes the proof.
3 Fixed point ratio and shuffle groups
In this section, we prove the reduction theorem (Theorem 1.3), which reduces the proof of Conjecture 1.2 to that of the
![]() $2$
-transitivity of
$2$
-transitivity of
![]() $G_{k,kn}$
. Recall from (1) that for
$G_{k,kn}$
. Recall from (1) that for
![]() $\tau \in \mathrm {Sym}([k])$
, the permutation
$\tau \in \mathrm {Sym}([k])$
, the permutation
![]() $\rho _\tau \in G_{k,kn}$
maps
$\rho _\tau \in G_{k,kn}$
maps
![]() $i+jn$
to
$i+jn$
to
![]() $i+j^\tau n$
for all
$i+j^\tau n$
for all
![]() $i\in [n]$
and
$i\in [n]$
and
![]() $j\in [k]$
. This leads to the following result on the fixed point ratio of
$j\in [k]$
. This leads to the following result on the fixed point ratio of
![]() $\rho _\tau $
, an observation that is the basis of our argument throughout this section.
$\rho _\tau $
, an observation that is the basis of our argument throughout this section.
Lemma 3.1. For each
![]() $\tau \in \mathrm {Sym}([k])$
, we have
$\tau \in \mathrm {Sym}([k])$
, we have
![]() $\mathrm {fpr}(\tau )=\mathrm {fpr}(\rho _{\tau })$
. In particular, if
$\mathrm {fpr}(\tau )=\mathrm {fpr}(\rho _{\tau })$
. In particular, if
![]() $\tau $
is a transposition, then
$\tau $
is a transposition, then
![]() $\mathrm {fpr}(\rho _{\tau })=(k-2)/k$
.
$\mathrm {fpr}(\rho _{\tau })=(k-2)/k$
.
A permutation group G on a set
![]() $\Omega $
is said to be primitive if the only partitions preserved by G are
$\Omega $
is said to be primitive if the only partitions preserved by G are
![]() $\{\Omega \}$
and
$\{\Omega \}$
and
![]() $\{\{\alpha \}\mid \alpha \in \Omega \}$
. It is well known and easy to see that every
$\{\{\alpha \}\mid \alpha \in \Omega \}$
. It is well known and easy to see that every
![]() $2$
-transitive group is primitive. An affine primitive group is a subgroup of
$2$
-transitive group is primitive. An affine primitive group is a subgroup of
![]() $\mathrm {AGL}(d,p)$
that contains the socle of
$\mathrm {AGL}(d,p)$
that contains the socle of
![]() $\mathrm {AGL}(d,p)$
, where d is a positive integer and p is prime.
$\mathrm {AGL}(d,p)$
, where d is a positive integer and p is prime.
Lemma 3.2. Suppose that
![]() $G_{k,kn}$
is an affine primitive group with
$G_{k,kn}$
is an affine primitive group with
![]() $k\geq 3$
. Then either
$k\geq 3$
. Then either
![]() $k=3$
and
$k=3$
and
![]() $n=1$
, or
$n=1$
, or
![]() $k=4$
and n is a power of
$k=4$
and n is a power of
![]() $2$
.
$2$
.
Proof. Let
![]() $G=G_{k,kn}$
, and let V be a d-dimension vector space over
$G=G_{k,kn}$
, and let V be a d-dimension vector space over
![]() $\mathbb {F}_p$
such that
$\mathbb {F}_p$
such that
![]() $G\leq \mathrm {AGL}(V)$
, where d is a positive integer and p is prime. Then
$G\leq \mathrm {AGL}(V)$
, where d is a positive integer and p is prime. Then
![]() $kn=|V|=p^d$
. By (1), there is a transposition
$kn=|V|=p^d$
. By (1), there is a transposition
![]() $\tau \in \mathrm {Sym}([k])$
such that
$\tau \in \mathrm {Sym}([k])$
such that
![]() $\rho _\tau $
fixes the zero vector
$\rho _\tau $
fixes the zero vector
![]() $0$
in V. It follows that
$0$
in V. It follows that
![]() $\rho _\tau \in G_0\leq \mathrm {GL}(V)$
. Since
$\rho _\tau \in G_0\leq \mathrm {GL}(V)$
. Since
![]() $\mathrm {Fix}(\rho _\tau )=\{v\in V\mid v^{\rho _\tau }=v\}$
is a subspace of V, we have
$\mathrm {Fix}(\rho _\tau )=\{v\in V\mid v^{\rho _\tau }=v\}$
is a subspace of V, we have
![]() $|\mathrm {Fix}(\rho _\tau )|=p^f$
for some nonnegative integer f. Thus, as
$|\mathrm {Fix}(\rho _\tau )|=p^f$
for some nonnegative integer f. Thus, as
![]() $\tau $
is a transposition, we derive from Lemma 3.1 that
$\tau $
is a transposition, we derive from Lemma 3.1 that
 $$\begin{align*}\frac{k-2}{k}=\mathrm{fpr}(\rho_\tau)=\frac{|\mathrm{Fix}(\rho_\tau)|}{|V|}=\frac{p^f}{p^d}=\frac{1}{p^{d-f}}. \end{align*}$$
$$\begin{align*}\frac{k-2}{k}=\mathrm{fpr}(\rho_\tau)=\frac{|\mathrm{Fix}(\rho_\tau)|}{|V|}=\frac{p^f}{p^d}=\frac{1}{p^{d-f}}. \end{align*}$$
Since
![]() $k\geq 3$
, this implies that either
$k\geq 3$
, this implies that either
![]() $k=p=3$
, or
$k=p=3$
, or
![]() $k=4$
and
$k=4$
and
![]() $p=2$
. For the latter,
$p=2$
. For the latter,
![]() $n=|V|/k=2^{d-2}$
is a power of
$n=|V|/k=2^{d-2}$
is a power of
![]() $2$
. Now assume that
$2$
. Now assume that
![]() $k=p=3$
. Then
$k=p=3$
. Then
![]() $n=|V|/k=p^d/k=3^{d-1}$
, and so (2) gives
$n=|V|/k=p^d/k=3^{d-1}$
, and so (2) gives
![]() $G=S_3\wr C_{d}$
. Since G is affine, we conclude that
$G=S_3\wr C_{d}$
. Since G is affine, we conclude that
![]() $d=1$
, which indicates that
$d=1$
, which indicates that
![]() $n=3^{d-1}=1$
.
$n=3^{d-1}=1$
.
A group is said to be almost simple if its socle is a nonabelian simple group. It follows from the well-known Burnside’s Theorem [Reference Burnside5, §154, Theorem XIII] that
![]() $2$
-transitive groups are either affine or almost simple.
$2$
-transitive groups are either affine or almost simple.
Proof of Theorem 1.3.
Let
![]() $G=G_{k,kn}$
be
$G=G_{k,kn}$
be
![]() $2$
-transitive with
$2$
-transitive with
![]() $k\geq 3$
. If G is affine, then according to Lemma 3.2, either
$k\geq 3$
. If G is affine, then according to Lemma 3.2, either
![]() $k=3$
and
$k=3$
and
![]() $n=1$
, or
$n=1$
, or
![]() $k=4$
and n is a power of
$k=4$
and n is a power of
![]() $2$
. The former leads to
$2$
. The former leads to
![]() $G=G_{3,3}=S_3$
, which satisfies the conclusion of the theorem. For the latter, since G is
$G=G_{3,3}=S_3$
, which satisfies the conclusion of the theorem. For the latter, since G is
![]() $2$
-transitive, we conclude from (2) that n is not a power of
$2$
-transitive, we conclude from (2) that n is not a power of
![]() $4$
, and so n is an odd power of
$4$
, and so n is an odd power of
![]() $2$
, again satisfying the conclusion of the theorem. Thus, we may assume that G is almost simple for the rest of the proof.
$2$
, again satisfying the conclusion of the theorem. Thus, we may assume that G is almost simple for the rest of the proof.
First assume that
![]() $k\geq 4$
. Take a transposition
$k\geq 4$
. Take a transposition
![]() $\tau \in \mathrm {Sym}([k])$
. By Lemma 3.1, we have
$\tau \in \mathrm {Sym}([k])$
. By Lemma 3.1, we have
Then since G is
![]() $2$
-transitive, it follows from [Reference Guralnick and Magaard10, Theorem 1] that either
$2$
-transitive, it follows from [Reference Guralnick and Magaard10, Theorem 1] that either
![]() $G\geq A_{kn}$
, or
$G\geq A_{kn}$
, or
The former satisfies the conclusion of the theorem. Now suppose that (4) holds. It follows that
This together with
![]() $\mathrm {fpr}(\rho _\tau )=(k-2)/k$
implies that
$\mathrm {fpr}(\rho _\tau )=(k-2)/k$
implies that
![]() $k<5$
. Thus,
$k<5$
. Thus,
![]() $k=4$
, which in turn yields
$k=4$
, which in turn yields
![]() $\mathrm {fpr}(\rho _\tau )=(k-2)/k=1/2$
, contradicting (4).
$\mathrm {fpr}(\rho _\tau )=(k-2)/k=1/2$
, contradicting (4).
In the following, assume that
![]() $k=3$
. For convenience in the coming discussion, we first calculate
$k=3$
. For convenience in the coming discussion, we first calculate
![]() $G_{3,3n}$
for
$G_{3,3n}$
for
![]() $n\leq 92$
by computation in Magma [Reference Bosma, Cannon and Playoust3]. It turns out that, for these values of n, if n is not a power of
$n\leq 92$
by computation in Magma [Reference Bosma, Cannon and Playoust3]. It turns out that, for these values of n, if n is not a power of
![]() $3$
, then
$3$
, then
![]() $G_{3,3n}$
contains
$G_{3,3n}$
contains
![]() $A_{3n}$
. Note by (2) that if n is a power of
$A_{3n}$
. Note by (2) that if n is a power of
![]() $3$
, then
$3$
, then
![]() $G_{3,3n}$
is not
$G_{3,3n}$
is not
![]() $2$
-transitive. Thus, in the remainder of the proof, we assume
$2$
-transitive. Thus, in the remainder of the proof, we assume
![]() $n>92$
.
$n>92$
.
Suppose for a contradiction that G does not contain
![]() $A_{3n}$
. Since
$A_{3n}$
. Since
![]() $n>92$
, it follows from the list of almost simple
$n>92$
, it follows from the list of almost simple
![]() $2$
-transitive groups (see [Reference Cameron6, Table 7.4]) that
$2$
-transitive groups (see [Reference Cameron6, Table 7.4]) that
![]() $\mathrm {Soc}(G)$
is a simple group of Lie type, say, over
$\mathrm {Soc}(G)$
is a simple group of Lie type, say, over
![]() $\mathbb {F}_q$
. In the following, we divide the proof into four cases according to
$\mathbb {F}_q$
. In the following, we divide the proof into four cases according to
![]() $q>4$
,
$q>4$
,
![]() $q=4$
,
$q=4$
,
![]() $q=3$
or
$q=3$
or
![]() $q=2$
. Take a transposition
$q=2$
. Take a transposition
![]() $\tau \in \mathrm {Sym}([3])$
. We have
$\tau \in \mathrm {Sym}([3])$
. We have
![]() $\mathrm {fpr}(\rho _\tau )=1/3$
by Lemma 3.1.
$\mathrm {fpr}(\rho _\tau )=1/3$
by Lemma 3.1.
Case 1:
![]() $q>4$
. In this case,
$q>4$
. In this case,
![]() $\mathrm {fpr}(\rho _\tau )=1/3>4/(3q)$
. Then since G is a
$\mathrm {fpr}(\rho _\tau )=1/3>4/(3q)$
. Then since G is a
![]() $2$
-transitive group on
$2$
-transitive group on
![]() $3n>276$
points, it follows from [Reference Liebeck and Saxl12, Theorem 1] that
$3n>276$
points, it follows from [Reference Liebeck and Saxl12, Theorem 1] that
![]() $\mathrm {Soc}(G)=\mathrm {PSL}(2,q)$
and
$\mathrm {Soc}(G)=\mathrm {PSL}(2,q)$
and
![]() $\mathrm {fpr}(\rho _\tau )$
is either
$\mathrm {fpr}(\rho _\tau )$
is either
![]() $2/(q+1)$
or
$2/(q+1)$
or
![]() $(q_0+1)/(q+1)$
, where
$(q_0+1)/(q+1)$
, where
![]() $q_0=q^{1/r}$
is a prime power for some integer
$q_0=q^{1/r}$
is a prime power for some integer
![]() $r\geq 2$
. This together with
$r\geq 2$
. This together with
![]() $\mathrm {fpr}(\rho _\tau )=1/3$
implies that
$\mathrm {fpr}(\rho _\tau )=1/3$
implies that
![]() $1/3=2/(q+1)$
or
$1/3=2/(q+1)$
or
![]() $1/3\leq (\sqrt {q}+1)/(q+1)$
. However, this leads to
$1/3\leq (\sqrt {q}+1)/(q+1)$
. However, this leads to
![]() $q\leq 9$
, and hence,
$q\leq 9$
, and hence,
![]() $3n=q+1\leq 10$
, a contradiction.
$3n=q+1\leq 10$
, a contradiction.
Case 2:
![]() $q=4$
. In this case, we see from [Reference Cameron6, Table 7.4] that G is a subgroup of either
$q=4$
. In this case, we see from [Reference Cameron6, Table 7.4] that G is a subgroup of either
![]() $\mathrm {P\Gamma U}(3,4)$
or
$\mathrm {P\Gamma U}(3,4)$
or
![]() $\mathrm {P\Gamma L}(d,4)$
with
$\mathrm {P\Gamma L}(d,4)$
with
![]() $d\geq 2$
, which together with
$d\geq 2$
, which together with
![]() $n>92$
implies that
$n>92$
implies that
![]() $G\leq \mathrm {P\Gamma L}(d,4)$
with
$G\leq \mathrm {P\Gamma L}(d,4)$
with
![]() $d\geq 3$
. Then according to [Reference Guralnick and Kantor9, Proposition 3.1], the fixed point ratio of a non-identity element in G is less than
$d\geq 3$
. Then according to [Reference Guralnick and Kantor9, Proposition 3.1], the fixed point ratio of a non-identity element in G is less than
 $$\begin{align*}\min\left\{\frac{1}{2},\ \frac{1}{4}+\frac{1}{4^{d-1}}\right\}=\frac{1}{4}+\frac{1}{4^{d-1}}\leq\frac{1}{4}+\frac{1}{4^2}<\frac{1}{3}, \end{align*}$$
$$\begin{align*}\min\left\{\frac{1}{2},\ \frac{1}{4}+\frac{1}{4^{d-1}}\right\}=\frac{1}{4}+\frac{1}{4^{d-1}}\leq\frac{1}{4}+\frac{1}{4^2}<\frac{1}{3}, \end{align*}$$
contradicting
![]() $\mathrm {fpr}(\rho _\tau )=1/3$
.
$\mathrm {fpr}(\rho _\tau )=1/3$
.
Case 3:
![]() $q=3$
. Recall that G is a
$q=3$
. Recall that G is a
![]() $2$
-transitive group on
$2$
-transitive group on
![]() $3n>276$
points. Then we see from [Reference Cameron6, Table 7.4] that G is a subgroup of
$3n>276$
points. Then we see from [Reference Cameron6, Table 7.4] that G is a subgroup of
![]() $\mathrm {PGL}(d,3)$
with
$\mathrm {PGL}(d,3)$
with
![]() $d\geq 6$
. It follows from Lemma 2.1 that
$d\geq 6$
. It follows from Lemma 2.1 that
for some nonnegative integers s and t. This yields
which is not possible.
Case 4:
![]() $q=2$
. In this case, we see from the list of almost simple
$q=2$
. In this case, we see from the list of almost simple
![]() $2$
-transitive groups that either
$2$
-transitive groups that either
![]() $G=\mathrm {PSL}(d,2)$
with
$G=\mathrm {PSL}(d,2)$
with
![]() $d\geq 3$
, or G is the group
$d\geq 3$
, or G is the group
![]() $\mathrm {Sp}(2m,2)$
for some
$\mathrm {Sp}(2m,2)$
for some
![]() $m\geq 3$
with point stabiliser
$m\geq 3$
with point stabiliser
![]() $\mathrm {O}^\pm (2m,2)$
.
$\mathrm {O}^\pm (2m,2)$
.
First assume
![]() $G=\mathrm {PSL}(d,2)$
with
$G=\mathrm {PSL}(d,2)$
with
![]() $d\geq 3$
. Then G can be viewed as
$d\geq 3$
. Then G can be viewed as
![]() $\mathrm {GL}(d,2)$
acting on the set of nonzero vectors. In this way,
$\mathrm {GL}(d,2)$
acting on the set of nonzero vectors. In this way,
![]() $\mathrm {Fix}(\rho _\tau )=\{v\in \mathbb {F}_2^d\mid v^x=v\}\setminus \{0\}$
, and so
$\mathrm {Fix}(\rho _\tau )=\{v\in \mathbb {F}_2^d\mid v^x=v\}\setminus \{0\}$
, and so
![]() $|\mathrm {Fix}(\rho _\tau )|=2^r-1$
for some nonnegative integer
$|\mathrm {Fix}(\rho _\tau )|=2^r-1$
for some nonnegative integer
![]() $r\leq d$
. It then follows from
$r\leq d$
. It then follows from
![]() $\mathrm {fpr}(\rho _\tau )=1/3$
that
$\mathrm {fpr}(\rho _\tau )=1/3$
that
This yields
Since the right-hand side of (5) is congruent to
![]() $2$
modulo
$2$
modulo
![]() $4$
, we deduce
$4$
, we deduce
![]() $3\cdot 2^r\equiv 2\ \pmod {4}$
, and thus,
$3\cdot 2^r\equiv 2\ \pmod {4}$
, and thus,
![]() $r=1$
. However, this leads to
$r=1$
. However, this leads to
![]() $6=2^d+2$
, contradicting
$6=2^d+2$
, contradicting
![]() $d\geq 3$
.
$d\geq 3$
.
Now assume
![]() $G=\mathrm {Sp}(2m,2)$
for some
$G=\mathrm {Sp}(2m,2)$
for some
![]() $m\geq 3$
with point stabiliser
$m\geq 3$
with point stabiliser
![]() $\mathrm {O}^\varepsilon (2m,2)$
, where
$\mathrm {O}^\varepsilon (2m,2)$
, where
![]() $\varepsilon \in \{+,-\}$
. Note that
$\varepsilon \in \{+,-\}$
. Note that
![]() $\rho _\tau $
is an involution with nonempty fixed point set. Let H be a point stabiliser of G containing
$\rho _\tau $
is an involution with nonempty fixed point set. Let H be a point stabiliser of G containing
![]() $\rho _\tau $
. According to [Reference Aschbacher and Seitz2, (8.5)], two involutions in H are conjugate in G if and only if they are conjugate in H. Hence,
$\rho _\tau $
. According to [Reference Aschbacher and Seitz2, (8.5)], two involutions in H are conjugate in G if and only if they are conjugate in H. Hence,
![]() $(\rho _\tau )^H=(\rho _\tau )^G\cap H$
. Then by [Reference Burness4, Lemma 1.2(iii)], we have
$(\rho _\tau )^H=(\rho _\tau )^G\cap H$
. Then by [Reference Burness4, Lemma 1.2(iii)], we have
 $$\begin{align*}\mathrm{fpr}(\rho_\tau)=\frac{|(\rho_\tau)^G\cap H|}{|(\rho_\tau)^G|}=\frac{|(\rho_\tau)^{H}|}{|(\rho_\tau)^{G}|} =\frac{|H|\cdot|\mathbf{C}_{G}(\rho_\tau)|}{|G|\cdot|\mathbf{C}_{H}(\rho_\tau)|} =\frac{|\mathrm{O}^\varepsilon(2m,2)|}{|\mathrm{Sp}(2m,2)|}\cdot\frac{|\mathbf{C}_{G}(\rho_\tau)|}{|\mathbf{C}_{H}(\rho_\tau)|}. \end{align*}$$
$$\begin{align*}\mathrm{fpr}(\rho_\tau)=\frac{|(\rho_\tau)^G\cap H|}{|(\rho_\tau)^G|}=\frac{|(\rho_\tau)^{H}|}{|(\rho_\tau)^{G}|} =\frac{|H|\cdot|\mathbf{C}_{G}(\rho_\tau)|}{|G|\cdot|\mathbf{C}_{H}(\rho_\tau)|} =\frac{|\mathrm{O}^\varepsilon(2m,2)|}{|\mathrm{Sp}(2m,2)|}\cdot\frac{|\mathbf{C}_{G}(\rho_\tau)|}{|\mathbf{C}_{H}(\rho_\tau)|}. \end{align*}$$
This in conjunction with Lemma 2.2 implies that
for some positive integer
![]() $r\leq m$
. According to whether
$r\leq m$
. According to whether
![]() $r=m$
or
$r=m$
or
![]() $r<m$
, we deduce that
$r<m$
, we deduce that
 $$\begin{align*}\mathrm{fpr}(\rho_\tau)=\frac{1}{2^{m-1}(2^m+\varepsilon1)}\cdot\frac{|\mathbf{O}_2(\mathbf{C}_{G}(\rho_\tau)|}{|\mathbf{O}_2(\mathbf{C}_{H}(\rho_\tau))|}\ \text{ or }\ \frac{2^{m-r-1}(2^{m-r}+\varepsilon1)}{2^{m-1}(2^m+\varepsilon1)} \cdot\frac{|\mathbf{O}_2(\mathbf{C}_{G}(\rho_\tau)|}{|\mathbf{O}_2(\mathbf{C}_{H}(\rho_\tau))|}. \end{align*}$$
$$\begin{align*}\mathrm{fpr}(\rho_\tau)=\frac{1}{2^{m-1}(2^m+\varepsilon1)}\cdot\frac{|\mathbf{O}_2(\mathbf{C}_{G}(\rho_\tau)|}{|\mathbf{O}_2(\mathbf{C}_{H}(\rho_\tau))|}\ \text{ or }\ \frac{2^{m-r-1}(2^{m-r}+\varepsilon1)}{2^{m-1}(2^m+\varepsilon1)} \cdot\frac{|\mathbf{O}_2(\mathbf{C}_{G}(\rho_\tau)|}{|\mathbf{O}_2(\mathbf{C}_{H}(\rho_\tau))|}. \end{align*}$$
Since
![]() $\mathrm {fpr}(\rho _\tau )=1/3$
and both
$\mathrm {fpr}(\rho _\tau )=1/3$
and both
![]() $|\mathbf {O}_2(\mathbf {C}_{G}(\rho _\tau )|$
and
$|\mathbf {O}_2(\mathbf {C}_{G}(\rho _\tau )|$
and
![]() $|\mathbf {O}_2(\mathbf {C}_{H}(\rho _\tau ))|$
are powers of
$|\mathbf {O}_2(\mathbf {C}_{H}(\rho _\tau ))|$
are powers of
![]() $2$
, it follows that
$2$
, it follows that
The former is not possible as
![]() $m\geq 3$
. For the latter, we obtain
$m\geq 3$
. For the latter, we obtain
and thus,
![]() $m-r=1$
, which in turn leads to
$m-r=1$
, which in turn leads to
![]() $m=3$
and
$m=3$
and
![]() $\varepsilon =+$
. However, this implies that
$\varepsilon =+$
. However, this implies that
![]() ${3n=|\mathrm {Sp}(6,2)|/|\mathrm {O}^+(6,2)|=36}$
, contradicting
${3n=|\mathrm {Sp}(6,2)|/|\mathrm {O}^+(6,2)|=36}$
, contradicting
![]() $n>92$
.
$n>92$
.
4
 $2$
-transitivity
$2$
-transitivity
We will prove Theorem 1.4 in this section. Throughout this section, let
![]() $n=k^st$
where s and t are integers satisfying
$n=k^st$
where s and t are integers satisfying
![]() $s\geq 0$
,
$s\geq 0$
,
![]() $t>1$
and
$t>1$
and
![]() $k\nmid t$
. For a nonnegative integer m and a positive integer
$k\nmid t$
. For a nonnegative integer m and a positive integer
![]() $\ell $
, we use
$\ell $
, we use
![]() $[m]_{\ell }^{0}$
and
$[m]_{\ell }^{0}$
and
![]() $[m]_{\ell }^{1}$
to denote the remainder and quotient of m divided by
$[m]_{\ell }^{1}$
to denote the remainder and quotient of m divided by
![]() $\ell $
; that is,
$\ell $
; that is,
with
![]() $0\leq [m]_{\ell }^{0}\leq \ell -1$
. For every
$0\leq [m]_{\ell }^{0}\leq \ell -1$
. For every
![]() $x\in [kn]$
(note that
$x\in [kn]$
(note that
![]() $0\le x<k^{s+1}t$
), we write
$0\le x<k^{s+1}t$
), we write
![]() $[x]_{t}^{1}$
in base k as follows:
$[x]_{t}^{1}$
in base k as follows:
![]() $[x]_{t}^{1}=k^sx_s+\cdots +kx_1+x_0$
, where
$[x]_{t}^{1}=k^sx_s+\cdots +kx_1+x_0$
, where
![]() $x_i\in [k]$
for every
$x_i\in [k]$
for every
![]() $i\in [s+1]$
. Therefore, x can be uniquely written as
$i\in [s+1]$
. Therefore, x can be uniquely written as
For convenience, we identify x with
![]() $(x_s,\ldots ,x_1,x_0;X)$
where
$(x_s,\ldots ,x_1,x_0;X)$
where
![]() $X=[x]_{t}^{0}$
, and sometimes we mix the two notations when doing addition. For example,
$X=[x]_{t}^{0}$
, and sometimes we mix the two notations when doing addition. For example,
Recall
![]() $(i+jn)^{\sigma }=ki+j$
for all
$(i+jn)^{\sigma }=ki+j$
for all
![]() $i\in [n]$
and
$i\in [n]$
and
![]() $j\in [k]$
. One can obtain inductively that
$j\in [k]$
. One can obtain inductively that
 $$ \begin{align} (x_s,\ldots,x_1,x_0;X)^{\sigma^{i}} &= \left(\sum_{j=i}^s k^{j}x_{j-i}\right)t+k^iX+\sum_{j=0}^{i-1}k^{i-1-j}x_{s-j}\nonumber\\ &=(x_{s-i},\ldots,x_1,x_0,0,\ldots,0;0)+k^iX+\sum_{j=0}^{i-1}k^{i-1-j}x_{s-j} \end{align} $$
$$ \begin{align} (x_s,\ldots,x_1,x_0;X)^{\sigma^{i}} &= \left(\sum_{j=i}^s k^{j}x_{j-i}\right)t+k^iX+\sum_{j=0}^{i-1}k^{i-1-j}x_{s-j}\nonumber\\ &=(x_{s-i},\ldots,x_1,x_0,0,\ldots,0;0)+k^iX+\sum_{j=0}^{i-1}k^{i-1-j}x_{s-j} \end{align} $$
for all
![]() $i\in [s+2]$
(when
$i\in [s+2]$
(when
![]() $i=s+1$
, the tuple
$i=s+1$
, the tuple
![]() $(x_{s-i},\ldots ,x_1,x_0,0,\ldots ,0;0)$
in equation (6) is to be understood as
$(x_{s-i},\ldots ,x_1,x_0,0,\ldots ,0;0)$
in equation (6) is to be understood as
![]() $0$
). In particular,
$0$
). In particular,
and thus,
Recalling from (1) that
![]() $(i+jn)^{\rho _{\tau }}=i+j^{\tau }n$
, we have
$(i+jn)^{\rho _{\tau }}=i+j^{\tau }n$
, we have
for every
![]() $(x_s,\ldots ,x_1,x_0;X)\in [kn]$
. By (6) and (9), it is clear that
$(x_s,\ldots ,x_1,x_0;X)\in [kn]$
. By (6) and (9), it is clear that
Consider the subgroup
![]() $H:=\langle \sigma ,\rho _{\tau }\mid \tau \in \mathrm {Sym}([k-1])\rangle $
of
$H:=\langle \sigma ,\rho _{\tau }\mid \tau \in \mathrm {Sym}([k-1])\rangle $
of
![]() $G_{k,kn}$
, which is contained in the stabiliser of
$G_{k,kn}$
, which is contained in the stabiliser of
![]() $kn-1$
. Our strategy for proving Theorem 1.4 is to prove that H is transitive on
$kn-1$
. Our strategy for proving Theorem 1.4 is to prove that H is transitive on
![]() $[kn-1]$
. We use
$[kn-1]$
. We use
![]() $(i,j)\in \mathrm {Sym}([k])$
with
$(i,j)\in \mathrm {Sym}([k])$
with
![]() $i\neq j$
to denote the transposition swapping i and j. For each
$i\neq j$
to denote the transposition swapping i and j. For each
![]() $x\in [k]$
, let
$x\in [k]$
, let
![]() $(0,x)$
denote the permutation of
$(0,x)$
denote the permutation of
![]() $[k]$
sending x to
$[k]$
sending x to
![]() $0$
and
$0$
and
![]() $0$
to x while fixing
$0$
to x while fixing
![]() $[k]\setminus \{0,x\}$
pointwise. In particular,
$[k]\setminus \{0,x\}$
pointwise. In particular,
![]() $(0,x)$
coincides with the above notation for a transposition if
$(0,x)$
coincides with the above notation for a transposition if
![]() $x\neq 0$
and is the identity permutation if
$x\neq 0$
and is the identity permutation if
![]() $x=0$
. This somewhat cumbersome notation avoids discussing whether
$x=0$
. This somewhat cumbersome notation avoids discussing whether
![]() $x=0$
in the following.
$x=0$
in the following.
Let
![]() $x=(x_s,x_{s-1},\ldots ,x_0;X)\in [kn]$
. Write
$x=(x_s,x_{s-1},\ldots ,x_0;X)\in [kn]$
. Write
![]() $\alpha _i=\sigma ^{i}\rho _{(0,1)}\sigma ^{-i}$
for every
$\alpha _i=\sigma ^{i}\rho _{(0,1)}\sigma ^{-i}$
for every
![]() $i\in [s+1]$
. By (10),
$i\in [s+1]$
. By (10),
Set
![]() $\beta _{\tau }=\sigma ^{-1}\rho _{\tau }\sigma \in H$
for
$\beta _{\tau }=\sigma ^{-1}\rho _{\tau }\sigma \in H$
for
![]() $\tau \in \mathrm {Sym}([k-1])$
. Using (7)–(9), it is straightforward to check that
$\tau \in \mathrm {Sym}([k-1])$
. Using (7)–(9), it is straightforward to check that
We will use the above two formulas for
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _{\tau }$
repeatedly without any reference. Let
$\beta _{\tau }$
repeatedly without any reference. Let
Lemma 4.1. If
![]() $T(x)=0$
, then
$T(x)=0$
, then
![]() $x\in 0^{H}$
.
$x\in 0^{H}$
.
Proof. It follows from
![]() $T(x)=0$
that
$T(x)=0$
that
![]() $x_i\neq k-1$
for
$x_i\neq k-1$
for
![]() $i\in [s+1]$
. This combined with (10) shows
$i\in [s+1]$
. This combined with (10) shows
and
![]() $\prod _{i=0}^s\sigma ^{s-i}\rho _{(0,x_i)}\sigma ^{-(s-i)}\in H$
. So it suffices to prove that
$\prod _{i=0}^s\sigma ^{s-i}\rho _{(0,x_i)}\sigma ^{-(s-i)}\in H$
. So it suffices to prove that
![]() $[t]\subseteq 0^H$
. We achieve this by showing that
$[t]\subseteq 0^H$
. We achieve this by showing that
![]() $x^H$
contains an integer less than x for each
$x^H$
contains an integer less than x for each
![]() $x\in [t]\setminus \{0\}$
.
$x\in [t]\setminus \{0\}$
.
Let
![]() $x\in [t]\setminus \{0\}$
. If
$x\in [t]\setminus \{0\}$
. If
![]() $[x]_{k}^{0}=0$
, then
$[x]_{k}^{0}=0$
, then
![]() $x^{\sigma ^{-1}} = x/k<x$
. If
$x^{\sigma ^{-1}} = x/k<x$
. If
![]() $[x]_{k}^{0}\neq 0$
and
$[x]_{k}^{0}\neq 0$
and
![]() $[x]_{k}^{0}\neq k-1$
, then
$[x]_{k}^{0}\neq k-1$
, then
![]() $x^{\beta _{\tau }}=x-[x]_k^0<x$
, where
$x^{\beta _{\tau }}=x-[x]_k^0<x$
, where
![]() $\tau =(0,[x]_k^0)$
. If
$\tau =(0,[x]_k^0)$
. If
![]() $[x]_{k}^{0}=k-1$
and
$[x]_{k}^{0}=k-1$
and
![]() $[t]_{k}^{0}\neq 1$
, then
$[t]_{k}^{0}\neq 1$
, then
![]() $[t+x]_{k}^{0}\notin \{0,k-1\}$
, and so there exists
$[t+x]_{k}^{0}\notin \{0,k-1\}$
, and so there exists
![]() $\tau \in \mathrm {Sym}([k-1])$
such that
$\tau \in \mathrm {Sym}([k-1])$
such that
![]() $([t+x]_{k}^{0})^{\tau }=[t+x]_{k}^{0}-1$
, which leads to
$([t+x]_{k}^{0})^{\tau }=[t+x]_{k}^{0}-1$
, which leads to
If
![]() $[x]_{k}^{0}=k-1$
and
$[x]_{k}^{0}=k-1$
and
![]() $[t]_{k}^{0}=1$
, then
$[t]_{k}^{0}=1$
, then
![]() $[t+x]_{k}^{0}=0$
, and hence,
$[t+x]_{k}^{0}=0$
, and hence,
Therefore,
![]() $[t]\subseteq 0^{H}$
, as desired.
$[t]\subseteq 0^{H}$
, as desired.
Lemma 4.2. Let
![]() $x=(x_{s},x_{s-1},\ldots ,x_1,x_0;X)\in [kn-1]$
. If
$x=(x_{s},x_{s-1},\ldots ,x_1,x_0;X)\in [kn-1]$
. If
![]() $1\leq T(x)\leq s$
, then there exists
$1\leq T(x)\leq s$
, then there exists
![]() ${y=(y_{s},y_{s-1},\ldots ,y_1,y_0;Y)\in x^{H}}$
such that either
${y=(y_{s},y_{s-1},\ldots ,y_1,y_0;Y)\in x^{H}}$
such that either
![]() $T(y)=0$
, or
$T(y)=0$
, or
![]() $y_0=0$
,
$y_0=0$
,
![]() $y_1=k-1$
and
$y_1=k-1$
and
![]() $T(x)\geq T(y)$
.
$T(x)\geq T(y)$
.
Proof. Let
![]() $\ell $
be the smallest integer such that
$\ell $
be the smallest integer such that
![]() $x_\ell \ne k-1$
. Write
$x_\ell \ne k-1$
. Write
Applying (8) repeatedly, we derive
![]() $z_{s-\ell }=x_s$
,
$z_{s-\ell }=x_s$
,
![]() $z_{s-\ell -1}=x_{s-1},\ldots ,z_{1}=x_{\ell +1}$
,
$z_{s-\ell -1}=x_{s-1},\ldots ,z_{1}=x_{\ell +1}$
,
![]() $z_0=x_{\ell }$
. Since
$z_0=x_{\ell }$
. Since
![]() $x_0=\cdots =x_{\ell -1}=k-1$
, it follows that
$x_0=\cdots =x_{\ell -1}=k-1$
, it follows that
![]() $T(x)\geq T(z)$
. If
$T(x)\geq T(z)$
. If
![]() $T(z)=0$
, then we confirm the lemma by taking
$T(z)=0$
, then we confirm the lemma by taking
![]() $y=z$
. In what follows, assume
$y=z$
. In what follows, assume
![]() $T(z)>0$
.
$T(z)>0$
.
Since
![]() $z_0=x_{\ell }\ne k-1$
and
$z_0=x_{\ell }\ne k-1$
and
![]() $k\geq 3$
, there exists
$k\geq 3$
, there exists
![]() $\tau \in \mathrm {Sym}([k-1])$
such that
$\tau \in \mathrm {Sym}([k-1])$
such that
![]() $|z_0^{\tau }-z_0|=1$
. Set
$|z_0^{\tau }-z_0|=1$
. Set
 $$ \begin{align*} \mu_0= \begin{cases} \sigma^{-1} & \text{if}~[z_0t+Z]_{k}^{0}\ne k-1 \\ \sigma^{s}\rho_{\tau}\sigma^{-s-1} & \text{if}~[z_0t+Z]_{k}^{0}=k-1. \end{cases} \end{align*} $$
$$ \begin{align*} \mu_0= \begin{cases} \sigma^{-1} & \text{if}~[z_0t+Z]_{k}^{0}\ne k-1 \\ \sigma^{s}\rho_{\tau}\sigma^{-s-1} & \text{if}~[z_0t+Z]_{k}^{0}=k-1. \end{cases} \end{align*} $$
Then by (8) and (10), we obtain
 $$ \begin{align*} z^{\mu_0}= \begin{cases} \left([z_0t+Z]_k^0,z_s,\ldots,z_1;[z_0t+Z]_k^1\right) & \text{if}~[z_0t+Z]_{k}^{0}\ne k-1 \\ \left([z_0^{\tau} t+Z]_k^0,z_s,\ldots,z_1;[z_0^{\tau}t+Z]_k^1\right) & \text{if}~[z_0t+Z]_{k}^{0}=k-1. \end{cases} \end{align*} $$
$$ \begin{align*} z^{\mu_0}= \begin{cases} \left([z_0t+Z]_k^0,z_s,\ldots,z_1;[z_0t+Z]_k^1\right) & \text{if}~[z_0t+Z]_{k}^{0}\ne k-1 \\ \left([z_0^{\tau} t+Z]_k^0,z_s,\ldots,z_1;[z_0^{\tau}t+Z]_k^1\right) & \text{if}~[z_0t+Z]_{k}^{0}=k-1. \end{cases} \end{align*} $$
If both
![]() $[z_0t+Z]_{k}^{0}$
and
$[z_0t+Z]_{k}^{0}$
and
![]() $[z_0^{\tau }t+Z]_{k}^{0}$
are equal to
$[z_0^{\tau }t+Z]_{k}^{0}$
are equal to
![]() $k-1$
, then it follows from
$k-1$
, then it follows from
![]() $|z_0^{\tau }-z_0|=1$
that k divides t, a contradiction. Thus,
$|z_0^{\tau }-z_0|=1$
that k divides t, a contradiction. Thus,
![]() $[z_0^{\tau }t+Z]_{k}^{0}\ne k-1$
if
$[z_0^{\tau }t+Z]_{k}^{0}\ne k-1$
if
![]() $[z_0t+Z]_{k}^{0}= k-1$
. Consequently,
$[z_0t+Z]_{k}^{0}= k-1$
. Consequently,
![]() $T(z^{\mu _0})=T(z)$
.
$T(z^{\mu _0})=T(z)$
.
Let j be the smallest integer such that
![]() $z_{j+1}=k-1$
. Since, in particular, none of
$z_{j+1}=k-1$
. Since, in particular, none of
![]() $z_1,\ldots ,z_{j-1}$
is equal to
$z_1,\ldots ,z_{j-1}$
is equal to
![]() $k-1$
, along the same lines as the above paragraph, we can take
$k-1$
, along the same lines as the above paragraph, we can take
![]() $\mu _1,\ldots ,\mu _{j-1}\in H$
such that
$\mu _1,\ldots ,\mu _{j-1}\in H$
such that
![]() $z^{\mu _0\mu _1\cdots \mu _{j-1}}=(w_{s},w_{s-1},\ldots ,w_1,w_0;W)$
with
$z^{\mu _0\mu _1\cdots \mu _{j-1}}=(w_{s},w_{s-1},\ldots ,w_1,w_0;W)$
with
![]() $w_0=z_j$
,
$w_0=z_j$
,
![]() $w_1=z_{j+1}$
and
$w_1=z_{j+1}$
and
Let
![]() $w=z^{\mu _0\mu _1\cdots \mu _{j-1}}$
and
$w=z^{\mu _0\mu _1\cdots \mu _{j-1}}$
and
![]() $y=w^{\sigma ^{s}\rho _{(0,w_0)}\sigma ^{-s}}$
. Since
$y=w^{\sigma ^{s}\rho _{(0,w_0)}\sigma ^{-s}}$
. Since
![]() $w_0=z_j\neq k-1$
and
$w_0=z_j\neq k-1$
and
![]() $w_1=z_{j+1}=k-1$
, it follows from (10) that
$w_1=z_{j+1}=k-1$
, it follows from (10) that
and
![]() $T(y)=T(w)$
. This together with
$T(y)=T(w)$
. This together with
![]() $\sigma ^{-\ell }\mu _0\mu _1\cdots \mu _{j-1}\sigma ^{s}\rho _{(0,w_0)}\sigma ^{-s}\in H$
and
$\sigma ^{-\ell }\mu _0\mu _1\cdots \mu _{j-1}\sigma ^{s}\rho _{(0,w_0)}\sigma ^{-s}\in H$
and
![]() $T(x)\geq T(z)=T(w)$
completes the proof.
$T(x)\geq T(z)=T(w)$
completes the proof.
Lemma 4.3. If
![]() $T(x)=s+1$
, then
$T(x)=s+1$
, then
![]() $x^H$
contains an integer less than x.
$x^H$
contains an integer less than x.
Proof. Since
![]() $x_i=k-1$
for every
$x_i=k-1$
for every
![]() $i\in [s+1]$
, we have
$i\in [s+1]$
, we have
Observe that (6) implies
 $$\begin{align*}x^{\sigma^{s+1}} =k^{s+1}X+(k-1)\sum_{i=0}^{s} k^i =k^{s+1}(X+1)-1. \end{align*}$$
$$\begin{align*}x^{\sigma^{s+1}} =k^{s+1}X+(k-1)\sum_{i=0}^{s} k^i =k^{s+1}(X+1)-1. \end{align*}$$
Since
![]() $x=k^{s+1}t-(t-X)=kn-(t-X)<kn-1$
, it follows that
$x=k^{s+1}t-(t-X)=kn-(t-X)<kn-1$
, it follows that
![]() $X<t-1$
, and so,
$X<t-1$
, and so,
Thus,
![]() $x>x^{\sigma ^{s+1}}$
.
$x>x^{\sigma ^{s+1}}$
.
Now we are ready to prove Theorem 1.4.
Proof of Theorem 1.4.
Recall our notation that
![]() $n=k^st$
with
$n=k^st$
with
![]() $s\geq 0$
,
$s\geq 0$
,
![]() $t>1$
and
$t>1$
and
![]() $k\nmid t$
, and H is the subgroup of
$k\nmid t$
, and H is the subgroup of
![]() $G_{k,kn}$
generated by
$G_{k,kn}$
generated by
![]() $\sigma $
and
$\sigma $
and
![]() $\rho _{\tau }$
for all
$\rho _{\tau }$
for all
![]() $\tau \in \mathrm {Sym}([k-1])$
. Then H is contained in the stabiliser of
$\tau \in \mathrm {Sym}([k-1])$
. Then H is contained in the stabiliser of
![]() $kn-1$
in
$kn-1$
in
![]() $G_{k,kn}$
. Since
$G_{k,kn}$
. Since
![]() $G_{k,kn}$
is transitive, it is
$G_{k,kn}$
is transitive, it is
![]() $2$
-transitive if H is transitive on
$2$
-transitive if H is transitive on
![]() $[kn-1]$
. Thus, it suffices to prove that
$[kn-1]$
. Thus, it suffices to prove that
![]() $[kn-1]\subseteq 0^H$
. Let
$[kn-1]\subseteq 0^H$
. Let
where
![]() $X\in [t]$
and
$X\in [t]$
and
![]() $x_i\in [k]$
for
$x_i\in [k]$
for
![]() $i\in [s+1]$
. Recall that
$i\in [s+1]$
. Recall that
![]() $T(x)=|\{i\in [s+1]\mid x_i=k-1\}|$
. We show
$T(x)=|\{i\in [s+1]\mid x_i=k-1\}|$
. We show
![]() $x\in 0^{H}$
for all
$x\in 0^{H}$
for all
![]() $x\in [kn-1]$
by induction on
$x\in [kn-1]$
by induction on
![]() $T(x)$
. The base case
$T(x)$
. The base case
![]() $T(x)=0$
has been confirmed by Lemma 4.1. Now let
$T(x)=0$
has been confirmed by Lemma 4.1. Now let
![]() $T(x)\geq 1$
and suppose that
$T(x)\geq 1$
and suppose that
![]() $y\in 0^{H}$
for all
$y\in 0^{H}$
for all
![]() $y\in [kn-1]$
with
$y\in [kn-1]$
with
![]() $T(y)<T(x)$
. We will complete the proof by constructing
$T(y)<T(x)$
. We will complete the proof by constructing
![]() $y\in x^H$
such that
$y\in x^H$
such that
![]() $T(y)<T(x)$
.
$T(y)<T(x)$
.
If
![]() $T(x)=s+1$
, then since x is finite, we derive by using Lemma 4.3 repeatedly that there exists
$T(x)=s+1$
, then since x is finite, we derive by using Lemma 4.3 repeatedly that there exists
![]() $y\in x^H$
with
$y\in x^H$
with
![]() $T(y)<T(x)$
. In the following, we assume that
$T(y)<T(x)$
. In the following, we assume that
![]() $1\le T(x)<s+1$
. By Lemma 4.2, we can further assume
$1\le T(x)<s+1$
. By Lemma 4.2, we can further assume
![]() $x=(x_s,\ldots ,x_2,k-1,0;X)$
. The proof proceeds in two cases.
$x=(x_s,\ldots ,x_2,k-1,0;X)$
. The proof proceeds in two cases.
Case 1:
![]() $[t]_k^0\neq k-1$
.
$[t]_k^0\neq k-1$
.
Let
![]() $z=(x_s,\ldots ,x_2,k-1,0;Z)$
, where
$z=(x_s,\ldots ,x_2,k-1,0;Z)$
, where
![]() $Z=X+1-[X+1]_k^0\equiv 0\ \pmod {k}$
. We first show in the next paragraph that
$Z=X+1-[X+1]_k^0\equiv 0\ \pmod {k}$
. We first show in the next paragraph that
![]() $z\in x^H$
.
$z\in x^H$
.
If
![]() $[X]_k^0\neq k-1$
, then letting
$[X]_k^0\neq k-1$
, then letting
![]() $\tau =(0, [X]_k^0)$
, we have
$\tau =(0, [X]_k^0)$
, we have
Now assume
![]() $[X]_k^0= k-1$
. Then
$[X]_k^0= k-1$
. Then
![]() $[t+X]_k^0\neq k-1$
and
$[t+X]_k^0\neq k-1$
and
![]() $[t+X]_k^0-[t]_k^0=-1$
. Letting
$[t+X]_k^0-[t]_k^0=-1$
. Letting
![]() $\tau =([t]_k^0, [t+X]_k^0)$
, we have
$\tau =([t]_k^0, [t+X]_k^0)$
, we have
 $$ \begin{align*} x^{\alpha_s\beta_{\tau}\alpha_s}&=(x_s,\ldots,x_2,k-1,0;X)^{\alpha_s\beta_{\tau}\alpha_s}\\ &=(x_s,\ldots,x_2,k-1,1;X)^{\beta_{\tau}\alpha_s}\\ &=(x_s,\ldots,x_2,k-1,1;X+[t]_k^0-[t+X]_k^0)^{\alpha_s}\\ &=(x_s,\ldots,x_2,k-1,0;X+1)\\ &=(x_s,\ldots,x_2,k-1,0;X+1-[X+1]_k^0)\\ &=(x_s,\ldots,x_2,k-1,0;Z). \end{align*} $$
$$ \begin{align*} x^{\alpha_s\beta_{\tau}\alpha_s}&=(x_s,\ldots,x_2,k-1,0;X)^{\alpha_s\beta_{\tau}\alpha_s}\\ &=(x_s,\ldots,x_2,k-1,1;X)^{\beta_{\tau}\alpha_s}\\ &=(x_s,\ldots,x_2,k-1,1;X+[t]_k^0-[t+X]_k^0)^{\alpha_s}\\ &=(x_s,\ldots,x_2,k-1,0;X+1)\\ &=(x_s,\ldots,x_2,k-1,0;X+1-[X+1]_k^0)\\ &=(x_s,\ldots,x_2,k-1,0;Z). \end{align*} $$
Therefore,
![]() $z=(x_s,\ldots ,x_2,k-1,0;Z)\in x^H$
.
$z=(x_s,\ldots ,x_2,k-1,0;Z)\in x^H$
.
In view of (8), we obtain that
and that, with
![]() $W:=(k-1)t+(Z+t-[t]_k^0)/k$
,
$W:=(k-1)t+(Z+t-[t]_k^0)/k$
,
 $$ \begin{align*} z^{\alpha_s\sigma^{-2}}&=(x_s,\ldots,x_2,k-1,1;Z)^{\sigma^{-2}}\\ &=\left([t]_k^0,x_s,\ldots,x_2,k-1;\frac{Z+t-[t]_k^0}{k}\right)^{\sigma^{-1}}=\left([W]_k^0,[t]_k^0,x_s,\ldots,x_2;[W]_k^1\right). \end{align*} $$
$$ \begin{align*} z^{\alpha_s\sigma^{-2}}&=(x_s,\ldots,x_2,k-1,1;Z)^{\sigma^{-2}}\\ &=\left([t]_k^0,x_s,\ldots,x_2,k-1;\frac{Z+t-[t]_k^0}{k}\right)^{\sigma^{-1}}=\left([W]_k^0,[t]_k^0,x_s,\ldots,x_2;[W]_k^1\right). \end{align*} $$
If
![]() $[(k-1)t+Z/k]_k^0\neq k-1$
or
$[(k-1)t+Z/k]_k^0\neq k-1$
or
![]() $[W]_k^0\neq k-1$
, then taking
$[W]_k^0\neq k-1$
, then taking
![]() $y=z^{\sigma ^{-2}}$
or
$y=z^{\sigma ^{-2}}$
or
![]() $y=z^{\alpha _s\sigma ^{-2}}$
, respectively, we have
$y=z^{\alpha _s\sigma ^{-2}}$
, respectively, we have
![]() $y\in z^H=x^H$
and
$y\in z^H=x^H$
and
![]() $T(y)=T(x)-1<T(x)$
. This completes the proof for the case
$T(y)=T(x)-1<T(x)$
. This completes the proof for the case
![]() $[(k-1)t+Z/k]_k^0\neq k-1$
or
$[(k-1)t+Z/k]_k^0\neq k-1$
or
![]() $[W]_k^0\neq k-1$
.
$[W]_k^0\neq k-1$
.
Next assume
![]() $[(k-1)t+Z/k]_k^0= k-1=[W]_k^0$
, or equivalently,
$[(k-1)t+Z/k]_k^0= k-1=[W]_k^0$
, or equivalently,
![]() $t-1\equiv Z/k\ \pmod {k}$
and
$t-1\equiv Z/k\ \pmod {k}$
and
![]() $(t-[t]_k^0)/k \equiv 0\ \pmod {k}$
. If
$(t-[t]_k^0)/k \equiv 0\ \pmod {k}$
. If
![]() $Z/k=1$
, then
$Z/k=1$
, then
![]() $[t]_k^0=2$
, which together with the assumption of Case 1 implies that
$[t]_k^0=2$
, which together with the assumption of Case 1 implies that
![]() $k>3$
, and hence,
$k>3$
, and hence,
![]() $\beta _{(0,2)}\in H$
. Thus, taking
$\beta _{(0,2)}\in H$
. Thus, taking
 $$ \begin{align*} y&=z^{\alpha_s\beta_{(0,2)}\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;k)^{\beta_{(0,2)}\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;k-2)^{\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,0;k-2)^{\sigma^{-2}}\\ &=(k-2,x_s,\ldots,x_2,k-1;0)^{\sigma^{-1}}\\ &=(k-2,k-2,x_s,\ldots,x_2; [(k-1)t]_k^1), \end{align*} $$
$$ \begin{align*} y&=z^{\alpha_s\beta_{(0,2)}\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;k)^{\beta_{(0,2)}\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;k-2)^{\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,0;k-2)^{\sigma^{-2}}\\ &=(k-2,x_s,\ldots,x_2,k-1;0)^{\sigma^{-1}}\\ &=(k-2,k-2,x_s,\ldots,x_2; [(k-1)t]_k^1), \end{align*} $$
we have
![]() $y\in z^H=x^H$
and
$y\in z^H=x^H$
and
![]() $T(y)=T(x)-1<T(x)$
, as desired. Similarly, if
$T(y)=T(x)-1<T(x)$
, as desired. Similarly, if
![]() $Z/k\geq 2$
, then as
$Z/k\geq 2$
, then as
![]() $[t+Z]_k^0=[t]_k^0\notin \{0,k-1\}$
, taking
$[t+Z]_k^0=[t]_k^0\notin \{0,k-1\}$
, taking
![]() $\tau =([t]_k^0, [t]_k^0-1)$
,
$\tau =([t]_k^0, [t]_k^0-1)$
,
![]() $\mu =(k-2 , k-3)$
and
$\mu =(k-2 , k-3)$
and
 $$ \begin{align*} y&=z^{\alpha_s\beta_{\tau}\alpha_s\sigma^{-1}\beta_{\mu}\sigma\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,0;Z-1)^{\sigma^{-1}\beta_{\mu}\sigma\alpha_s\sigma^{-2}}\\ &=(k-1,x_s,\ldots,x_2,k-1;Z/k-1)^{\beta_{\mu}\sigma\alpha_s\sigma^{-2}}\\ &=(k-1,x_s,\ldots,x_2,k-1;Z/k-2)^{\sigma\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;Z-k-1)^{\sigma^{-2}}\\ &=\left([t-1]_k^0, x_s,\ldots,x_2,k-1;\frac{Z+t-[t]_k^0}{k}-1\right)^{\sigma^{-1}}\\ &=([W-1]_k^0,[t-1]_k^0, x_s,\ldots,x_2;[W-1]_k^1)\\ &=(k-2,[t-1]_k^0, x_s,\ldots,x_2;[W-1]_k^1), \end{align*} $$
$$ \begin{align*} y&=z^{\alpha_s\beta_{\tau}\alpha_s\sigma^{-1}\beta_{\mu}\sigma\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,0;Z-1)^{\sigma^{-1}\beta_{\mu}\sigma\alpha_s\sigma^{-2}}\\ &=(k-1,x_s,\ldots,x_2,k-1;Z/k-1)^{\beta_{\mu}\sigma\alpha_s\sigma^{-2}}\\ &=(k-1,x_s,\ldots,x_2,k-1;Z/k-2)^{\sigma\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;Z-k-1)^{\sigma^{-2}}\\ &=\left([t-1]_k^0, x_s,\ldots,x_2,k-1;\frac{Z+t-[t]_k^0}{k}-1\right)^{\sigma^{-1}}\\ &=([W-1]_k^0,[t-1]_k^0, x_s,\ldots,x_2;[W-1]_k^1)\\ &=(k-2,[t-1]_k^0, x_s,\ldots,x_2;[W-1]_k^1), \end{align*} $$
we have
![]() $y\in z^H=x^H$
and
$y\in z^H=x^H$
and
![]() $T(y)=T(x)-1<T(x)$
, as desired. If
$T(y)=T(x)-1<T(x)$
, as desired. If
![]() $Z=0$
, then
$Z=0$
, then
![]() $[t]_k^0=1$
, which implies that
$[t]_k^0=1$
, which implies that
and then the previous two sentences show that there exists
![]() $y\in (z^{\alpha _s\beta _{(0,1)}})^H=x^H$
with
$y\in (z^{\alpha _s\beta _{(0,1)}})^H=x^H$
with
![]() $T(y)<T(x)$
.
$T(y)<T(x)$
.
Case 2:
![]() $[t]_{k}^{0}=k-1$
.
$[t]_{k}^{0}=k-1$
.
Recall that
![]() $x=(x_s,\ldots ,x_2,k-1,0;X)$
. Let
$x=(x_s,\ldots ,x_2,k-1,0;X)$
. Let
where
![]() $U=(X-[X]_k^0)/k$
and
$U=(X-[X]_k^0)/k$
and
![]() $V=(t+X+1-[X]_k^0)/k$
. We first show that
$V=(t+X+1-[X]_k^0)/k$
. We first show that
![]() $u,v\in x^H$
.
$u,v\in x^H$
.
If
![]() $[X]_{k}^{0}=k-1$
, then
$[X]_{k}^{0}=k-1$
, then
![]() $[t+X]_k^0=k-2$
, and it follows that
$[t+X]_k^0=k-2$
, and it follows that
 $$ \begin{align*} x^{\alpha_s\beta_{(k-2,k-3)}\alpha_s\beta_{(0,k-2)}\sigma^{-1}} &= (x_s,\ldots,x_2,k-1,1;X)^{\beta_{(k-2,k-3)}\alpha_s\beta_{(0,k-2)}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,1;X-1)^{\alpha_s\beta_{(0,k-2)}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,0;X-1)^{\beta_{(0,k-2)}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,0;X-k+1)^{\sigma^{-1}}\\ &= (0,x_s,\ldots,x_2,k-1;U)\\ &= u. \end{align*} $$
$$ \begin{align*} x^{\alpha_s\beta_{(k-2,k-3)}\alpha_s\beta_{(0,k-2)}\sigma^{-1}} &= (x_s,\ldots,x_2,k-1,1;X)^{\beta_{(k-2,k-3)}\alpha_s\beta_{(0,k-2)}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,1;X-1)^{\alpha_s\beta_{(0,k-2)}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,0;X-1)^{\beta_{(0,k-2)}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,0;X-k+1)^{\sigma^{-1}}\\ &= (0,x_s,\ldots,x_2,k-1;U)\\ &= u. \end{align*} $$
If
![]() $[X]_{k}^{0}\neq k-1$
, then letting
$[X]_{k}^{0}\neq k-1$
, then letting
![]() $\tau =(0,[X]_k^0)$
, we have
$\tau =(0,[X]_k^0)$
, we have
Hence, it always holds that
![]() $u\in x^H$
. If
$u\in x^H$
. If
![]() $[t+X]_{k}^{0}=k-1$
, then
$[t+X]_{k}^{0}=k-1$
, then
![]() $[X]_k^0=0$
, and thus,
$[X]_k^0=0$
, and thus,
 $$ \begin{align*} x^{\beta_{(0,1)}\alpha_s\sigma^{-1}}&=(x_s,\ldots,x_2,k-1,0;X+1)^{\alpha_s\sigma^{-1}} \\ &= (x_s,\ldots,x_2,k-1,1;X+1)^{\sigma^{-1}}=(0,x_s,\ldots,x_2,k-1;V)=v. \end{align*} $$
$$ \begin{align*} x^{\beta_{(0,1)}\alpha_s\sigma^{-1}}&=(x_s,\ldots,x_2,k-1,0;X+1)^{\alpha_s\sigma^{-1}} \\ &= (x_s,\ldots,x_2,k-1,1;X+1)^{\sigma^{-1}}=(0,x_s,\ldots,x_2,k-1;V)=v. \end{align*} $$
If
![]() $[t+X]_{k}^{0}\neq k-1$
, then as
$[t+X]_{k}^{0}\neq k-1$
, then as
![]() $[t+X]_k^0=[X]_k^0-1$
, we obtain by taking
$[t+X]_k^0=[X]_k^0-1$
, we obtain by taking
![]() $\tau =(0,[t+X]_k^0)$
that
$\tau =(0,[t+X]_k^0)$
that
 $$ \begin{align*} x^{\alpha_s\beta_{\tau}\sigma^{-1}} &= (x_s,\ldots,x_2,k-1,1;X)^{\beta_{\tau}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,1;X-[t+X]_k^0)^{\sigma^{-1}}=(0,x_s,\ldots,x_2,k-1;V)=v. \end{align*} $$
$$ \begin{align*} x^{\alpha_s\beta_{\tau}\sigma^{-1}} &= (x_s,\ldots,x_2,k-1,1;X)^{\beta_{\tau}\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,1;X-[t+X]_k^0)^{\sigma^{-1}}=(0,x_s,\ldots,x_2,k-1;V)=v. \end{align*} $$
Therefore,
![]() $v\in x^H$
always holds as well.
$v\in x^H$
always holds as well.
Now we have proved
![]() $u,v \in x^H$
. If
$u,v \in x^H$
. If
![]() $[(k-1)t+U]_{k}^{0}\neq k-1$
, then since
$[(k-1)t+U]_{k}^{0}\neq k-1$
, then since
it follows that
![]() $u^{\sigma ^{-1}}\in x^H$
with
$u^{\sigma ^{-1}}\in x^H$
with
![]() $T(u^{\sigma ^{-1}})=T(x)-1<T(x)$
. Similarly, if
$T(u^{\sigma ^{-1}})=T(x)-1<T(x)$
. Similarly, if
![]() $[(k-1)t+V]_{k}^{0}\neq k-1$
, then
$[(k-1)t+V]_{k}^{0}\neq k-1$
, then
![]() $v^{\sigma ^{-1}}\in x^H$
with
$v^{\sigma ^{-1}}\in x^H$
with
![]() $T(v^{\sigma ^{-1}})=T(x)-1<T(x)$
. This completes the proof for the case
$T(v^{\sigma ^{-1}})=T(x)-1<T(x)$
. This completes the proof for the case
![]() $[(k-1)t+U]_{k}^{0}\ne k-1$
or
$[(k-1)t+U]_{k}^{0}\ne k-1$
or
![]() $[(k-1)t+V]_{k}^{0}\neq k-1$
.
$[(k-1)t+V]_{k}^{0}\neq k-1$
.
Next assume
![]() $[(k-1)t+U]_{k}^{0}=k-1=[(k-1)t+V]_{k}^{0}$
. Since
$[(k-1)t+U]_{k}^{0}=k-1=[(k-1)t+V]_{k}^{0}$
. Since
![]() $X-[X]_k^0\leq X\leq t-1$
,
$X-[X]_k^0\leq X\leq t-1$
,
 $$ \begin{align*} u^{\sigma\alpha_s\sigma^{-1}}&= (x_s,\ldots,x_2,k-1,0;X-[X]_k^0)^{\alpha_s\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,1;X-[X]_k^0)^{\sigma^{-1}} = (k-1,x_s,\ldots,x_2,k-1;V-1). \end{align*} $$
$$ \begin{align*} u^{\sigma\alpha_s\sigma^{-1}}&= (x_s,\ldots,x_2,k-1,0;X-[X]_k^0)^{\alpha_s\sigma^{-1}}\\ &= (x_s,\ldots,x_2,k-1,1;X-[X]_k^0)^{\sigma^{-1}} = (k-1,x_s,\ldots,x_2,k-1;V-1). \end{align*} $$
Moreover, we deduce from
![]() $[(k-1)t+U]_{k}^{0}=k-1$
that
$[(k-1)t+U]_{k}^{0}=k-1$
that
![]() $U\geq [U]_k^0=k-2\geq 1$
, which implies
$U\geq [U]_k^0=k-2\geq 1$
, which implies
![]() $V\geq 2$
and
$V\geq 2$
and
![]() $0\leq X-[X]_k^0-k\leq t-1$
. This combined with
$0\leq X-[X]_k^0-k\leq t-1$
. This combined with
![]() $[(k-1)t+U]_{k}^{0}=k-1=[(k-1)t+V]_{k}^{0}$
yields that
$[(k-1)t+U]_{k}^{0}=k-1=[(k-1)t+V]_{k}^{0}$
yields that
 $$ \begin{align*} u^{\sigma\alpha_s\sigma^{-1}\beta_{(k-2,k-3)}\sigma\alpha_s\sigma^{-2}}& =(k-1,x_s,\ldots,x_2,k-1;V-1)^{\beta_{(k-2,k-3)}\sigma\alpha_s\sigma^{-2}}\\ &=(k-1,x_s,\ldots,x_2,k-1;V-2)^{\sigma\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;X-[X]_k^0-k)^{\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,0;X-[X]_k^0-k)^{\sigma^{-2}}\\ &=(0,x_s,\ldots,x_2,k-1;U-1)^{\sigma^{-1}}\\ &=(k-2,0,x_s,\ldots,x_2;[(k-1)t+U-1]_k^1). \end{align*} $$
$$ \begin{align*} u^{\sigma\alpha_s\sigma^{-1}\beta_{(k-2,k-3)}\sigma\alpha_s\sigma^{-2}}& =(k-1,x_s,\ldots,x_2,k-1;V-1)^{\beta_{(k-2,k-3)}\sigma\alpha_s\sigma^{-2}}\\ &=(k-1,x_s,\ldots,x_2,k-1;V-2)^{\sigma\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,1;X-[X]_k^0-k)^{\alpha_s\sigma^{-2}}\\ &=(x_s,\ldots,x_2,k-1,0;X-[X]_k^0-k)^{\sigma^{-2}}\\ &=(0,x_s,\ldots,x_2,k-1;U-1)^{\sigma^{-1}}\\ &=(k-2,0,x_s,\ldots,x_2;[(k-1)t+U-1]_k^1). \end{align*} $$
As a consequence, with
![]() $y:=u^{\sigma \alpha _s\sigma ^{-1}\beta _{(k-2,k-3)}\sigma \alpha _s\sigma ^{-2}}\in u^H=x^H$
, we finally obtain that
$y:=u^{\sigma \alpha _s\sigma ^{-1}\beta _{(k-2,k-3)}\sigma \alpha _s\sigma ^{-2}}\in u^H=x^H$
, we finally obtain that
![]() $T(y)=T(x)-1<T(x)$
.
$T(y)=T(x)-1<T(x)$
.
5 Open problems on generalised shuffle groups
Shuffle groups on
![]() $kn$
cards can be considered in a more general way by restricting the permutations on the set of k piles to a subgroup of
$kn$
cards can be considered in a more general way by restricting the permutations on the set of k piles to a subgroup of
![]() $\mathrm {Sym}([k])$
. Precisely, if
$\mathrm {Sym}([k])$
. Precisely, if
![]() $P\leq \mathrm {Sym}([k])$
is a group of permutations on the set of k piles, then we define the generalised shuffle group on
$P\leq \mathrm {Sym}([k])$
is a group of permutations on the set of k piles, then we define the generalised shuffle group on
![]() $kn$
cards with respect to P by
$kn$
cards with respect to P by
where
![]() $\sigma $
is the standard shuffle and
$\sigma $
is the standard shuffle and
![]() $\rho _\tau $
is the permutation on
$\rho _\tau $
is the permutation on
![]() $kn$
cards induced by the permutation
$kn$
cards induced by the permutation
![]() $\tau $
on the k piles. In particular,
$\tau $
on the k piles. In particular,
![]() $\mathrm {Sh}(\mathrm {Sym}([k]),n)$
is exactly the group
$\mathrm {Sh}(\mathrm {Sym}([k]),n)$
is exactly the group
![]() $G_{k,kn}$
studied in this paper. Generalised shuffle groups are introduced and systematically studied by Amarra, Morgan and Praeger in [Reference Amarra, Morgan and Praeger1]. Among several open problems, a conjecture [Reference Amarra, Morgan and Praeger1, Conjecture 1.10] made by them is that if
$G_{k,kn}$
studied in this paper. Generalised shuffle groups are introduced and systematically studied by Amarra, Morgan and Praeger in [Reference Amarra, Morgan and Praeger1]. Among several open problems, a conjecture [Reference Amarra, Morgan and Praeger1, Conjecture 1.10] made by them is that if
![]() $k\geq 3$
, n is not a power of k and
$k\geq 3$
, n is not a power of k and
![]() $(k,n)\neq (4,2^f)$
for any positive integer f, then
$(k,n)\neq (4,2^f)$
for any positive integer f, then
![]() $\mathrm {Sh}(C_k,n)$
contains
$\mathrm {Sh}(C_k,n)$
contains
![]() $A_{kn}$
, where
$A_{kn}$
, where
![]() $C_k$
is generated by the k-cycle
$C_k$
is generated by the k-cycle
![]() $(0,1,\ldots ,k-1)\in \mathrm {Sym}([k])$
.
$(0,1,\ldots ,k-1)\in \mathrm {Sym}([k])$
.
Note that
![]() $\mathrm {Sh}(C_k,n)=\langle \sigma , \rho _{(0,1,\ldots ,k-1)}\sigma \rangle $
. Hence, the above-mentioned conjecture asserts that, somewhat surprisingly, two shuffles
$\mathrm {Sh}(C_k,n)=\langle \sigma , \rho _{(0,1,\ldots ,k-1)}\sigma \rangle $
. Hence, the above-mentioned conjecture asserts that, somewhat surprisingly, two shuffles
![]() $\sigma $
and
$\sigma $
and
![]() $\rho _{(0,1,\ldots ,k-1)}\sigma $
are enough to generate
$\rho _{(0,1,\ldots ,k-1)}\sigma $
are enough to generate
![]() $A_{kn}$
or
$A_{kn}$
or
![]() $S_{kn}$
. This suggests that a ‘best possible’ improvement to Theorem 1.5 would be the determination of
$S_{kn}$
. This suggests that a ‘best possible’ improvement to Theorem 1.5 would be the determination of
![]() $\mathrm {Sh}(C_k,n)$
. It is shown in [Reference Amarra, Morgan and Praeger1, Theorem 1.4(1)] that if
$\mathrm {Sh}(C_k,n)$
. It is shown in [Reference Amarra, Morgan and Praeger1, Theorem 1.4(1)] that if
![]() $kn=k^m$
, then
$kn=k^m$
, then
for any
![]() $P\leq \mathrm {Sym}([k])$
. If
$P\leq \mathrm {Sym}([k])$
. If
![]() $k=4$
and
$k=4$
and
![]() $kn=2^m$
with m odd, then similarly to the proof of [Reference Cohen, Harmse, Morrison and Wright7, Theorem 2.6], we derive that
$kn=2^m$
with m odd, then similarly to the proof of [Reference Cohen, Harmse, Morrison and Wright7, Theorem 2.6], we derive that
According to [Reference Medvedoff and Morrison13, Lemma 2], the standard shuffle
![]() $\sigma $
is an even permutation if and only if
$\sigma $
is an even permutation if and only if
Observing that
![]() $\rho _{(0,1,\ldots ,k-1)}$
is a product of n cycles of length k, we obtain that
$\rho _{(0,1,\ldots ,k-1)}$
is a product of n cycles of length k, we obtain that
![]() $\rho _{(0,1,\ldots ,k-1)}$
is even if and only if
$\rho _{(0,1,\ldots ,k-1)}$
is even if and only if
![]() $(k-1)n$
is even. Hence,
$(k-1)n$
is even. Hence,
![]() $\mathrm {Sh}(C_k,n)\leq A_{kn}$
if and only if
$\mathrm {Sh}(C_k,n)\leq A_{kn}$
if and only if
This together with (11) and (12) indicates that [Reference Amarra, Morgan and Praeger1, Conjecture 1.10] is essentially the following conjectural classification of
![]() $\mathrm {Sh}(C_k,n)$
for all
$\mathrm {Sh}(C_k,n)$
for all
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n\geq 1$
.
$n\geq 1$
.
Conjecture 5.1. If
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $C_k=\langle (0,1,\ldots ,k-1)\rangle \leq \mathrm {Sym}([k])$
, then the following hold:
$C_k=\langle (0,1,\ldots ,k-1)\rangle \leq \mathrm {Sym}([k])$
, then the following hold:
-
(a) If
 $kn=k^m$
, then
$kn=k^m$
, then
 $\mathrm {Sh}(C_k,n)$
is the primitive wreath product
$\mathrm {Sh}(C_k,n)$
is the primitive wreath product
 $C_k\wr C_m$
.
$C_k\wr C_m$
. -
(b) If
 $k=4$
and
$k=4$
and
 $kn=2^m$
with m odd, then
$kn=2^m$
with m odd, then
 $\mathrm {Sh}(C_k,n)$
is the affine group
$\mathrm {Sh}(C_k,n)$
is the affine group
 $\mathrm {AGL}(m,2)$
.
$\mathrm {AGL}(m,2)$
. -
(c) If n is not a power of k and either
 $k(k-1)n(n-1)/4$
or
$k(k-1)n(n-1)/4$
or
 $(k-1)n$
is odd, then
$(k-1)n$
is odd, then
 $\mathrm {Sh}(C_k,n)=S_{kn}$
.
$\mathrm {Sh}(C_k,n)=S_{kn}$
. -
(d) In all other cases,
 $\mathrm {Sh}(C_k,n)=A_{kn}$
.
$\mathrm {Sh}(C_k,n)=A_{kn}$
.
A choice of P to make
![]() $\mathrm {Sh}(P,n)$
close to
$\mathrm {Sh}(P,n)$
close to
![]() $G_{k,kn}$
is
$G_{k,kn}$
is
![]() $P=A_k$
. For the case
$P=A_k$
. For the case
![]() $kn=k^m$
, it is already known (see (11)) that
$kn=k^m$
, it is already known (see (11)) that
![]() $\mathrm {Sh}(A_k,n)=A_k\wr C_m$
. Moreover, since
$\mathrm {Sh}(A_k,n)=A_k\wr C_m$
. Moreover, since
![]() $\rho _\tau $
is even for each
$\rho _\tau $
is even for each
![]() $\tau \in A_k$
, the parity of
$\tau \in A_k$
, the parity of
![]() $\sigma $
implies that
$\sigma $
implies that
![]() $\mathrm {Sh}(A_k,n)\leq A_{kn}$
if and only if (13) holds. Therefore, we pose the following conjectural classification of
$\mathrm {Sh}(A_k,n)\leq A_{kn}$
if and only if (13) holds. Therefore, we pose the following conjectural classification of
![]() $\mathrm {Sh}(A_k,n)$
for all
$\mathrm {Sh}(A_k,n)$
for all
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n\geq 1$
.
$n\geq 1$
.
Conjecture 5.2. If
![]() $k\geq 3$
, then the following hold:
$k\geq 3$
, then the following hold:
-
(a) If
 $kn=k^m$
, then
$kn=k^m$
, then
 $\mathrm {Sh}(A_k,n)$
is the primitive wreath product
$\mathrm {Sh}(A_k,n)$
is the primitive wreath product
 $A_k\wr C_m$
.
$A_k\wr C_m$
. -
(b) If
 $k=4$
and
$k=4$
and
 $kn=2^m$
with m odd, then
$kn=2^m$
with m odd, then
 $\mathrm {Sh}(A_k,n)$
is the affine group
$\mathrm {Sh}(A_k,n)$
is the affine group
 $\mathrm {AGL}(m,2)$
.
$\mathrm {AGL}(m,2)$
. -
(c) If n is not a power of k and
 $k(k-1)n(n-1)/4$
is odd, then
$k(k-1)n(n-1)/4$
is odd, then
 $\mathrm {Sh}(A_k,n)=S_{kn}$
.
$\mathrm {Sh}(A_k,n)=S_{kn}$
. -
(d) In all other cases,
 $\mathrm {Sh}(A_k,n)=A_{kn}$
.
$\mathrm {Sh}(A_k,n)=A_{kn}$
.
Proving this conjecture should be easier than proving Conjecture 5.1. For one reason, if k is odd, then
![]() $\mathrm {Sh}(C_k,n)\leq \mathrm {Sh}(A_k,n)$
, and so the conclusion of Conjecture 5.2 is weaker in this case. For another reason, Conjecture 5.2 is closer to our Theorem 1.5 in the sense that the size of P is only reduced by half from
$\mathrm {Sh}(C_k,n)\leq \mathrm {Sh}(A_k,n)$
, and so the conclusion of Conjecture 5.2 is weaker in this case. For another reason, Conjecture 5.2 is closer to our Theorem 1.5 in the sense that the size of P is only reduced by half from
![]() $P=S_k$
to
$P=S_k$
to
![]() $P=A_k$
. Thus, some ideas in the proof of Theorem 1.5 also apply to Conjecture 5.2. For example,
$P=A_k$
. Thus, some ideas in the proof of Theorem 1.5 also apply to Conjecture 5.2. For example,
![]() $\rho _{(0,1,2)}\in \mathrm {Sh}(A_k,n)$
has fixed point ratio
$\rho _{(0,1,2)}\in \mathrm {Sh}(A_k,n)$
has fixed point ratio
![]() $(k-3)/k$
, which is at least
$(k-3)/k$
, which is at least
![]() $1/2$
when
$1/2$
when
![]() $k\geq 6$
. In this way, a parallel result to Theorem 1.3 might still be established by the approach of this paper with an ad hoc treatment for
$k\geq 6$
. In this way, a parallel result to Theorem 1.3 might still be established by the approach of this paper with an ad hoc treatment for
![]() $k\in \{3,4,5\}$
. However, we anticipate more work to be done to prove the
$k\in \{3,4,5\}$
. However, we anticipate more work to be done to prove the
![]() $2$
-transitivity of
$2$
-transitivity of
![]() $\mathrm {Sh}(A_k,n)$
.
$\mathrm {Sh}(A_k,n)$
.
As a contrast to
![]() $P=C_k$
or
$P=C_k$
or
![]() $A_k$
, the choice
$A_k$
, the choice
![]() $P=\langle \mathrm {Rev}(k)\rangle $
from [Reference Medvedoff and Morrison13, Page 6], where
$P=\langle \mathrm {Rev}(k)\rangle $
from [Reference Medvedoff and Morrison13, Page 6], where
![]() $\mathrm {Rev}(k)$
is the permutation on
$\mathrm {Rev}(k)$
is the permutation on
![]() $[k]$
sending i to
$[k]$
sending i to
![]() $k-1-i$
, will make
$k-1-i$
, will make
![]() $\mathrm {Sh}(P,n)$
never equal to
$\mathrm {Sh}(P,n)$
never equal to
![]() $G_{k,kn}$
. In fact, denoting
$G_{k,kn}$
. In fact, denoting
and
![]() $B_i=\{i,kn-1-i\}$
(can be a singleton if
$B_i=\{i,kn-1-i\}$
(can be a singleton if
![]() $i=kn-i-1$
) for
$i=kn-i-1$
) for
![]() $i\in \{0,1,\ldots , \lfloor (kn-1)/2 \rfloor \}$
, we can verify directly that
$i\in \{0,1,\ldots , \lfloor (kn-1)/2 \rfloor \}$
, we can verify directly that
![]() $R_{k,kn}$
preserves the set
$R_{k,kn}$
preserves the set
![]() $\{B_0,B_1,\ldots ,B_{\lfloor (kn-1)/2 \rfloor }\}$
. If
$\{B_0,B_1,\ldots ,B_{\lfloor (kn-1)/2 \rfloor }\}$
. If
![]() $kn$
is even, then
$kn$
is even, then
![]() $\{B_0,B_1,\ldots ,B_{\lfloor (kn-1)/2 \rfloor }\}$
is a block system of
$\{B_0,B_1,\ldots ,B_{\lfloor (kn-1)/2 \rfloor }\}$
is a block system of
![]() $R_{k,kn}$
, and so
$R_{k,kn}$
, and so
![]() $R_{k,kn}\leq C_2\wr S_{kn/2}$
is imprimitive. If
$R_{k,kn}\leq C_2\wr S_{kn/2}$
is imprimitive. If
![]() $kn$
is odd, then
$kn$
is odd, then
![]() $R_{k,kn}$
fixes the
$R_{k,kn}$
fixes the
![]() $((kn-1)/2)$
-th card and preserves the partition
$((kn-1)/2)$
-th card and preserves the partition
![]() $\{B_0,B_1,\ldots ,B_{\lfloor (kn-1)/2 \rfloor -1}\}$
of the rest
$\{B_0,B_1,\ldots ,B_{\lfloor (kn-1)/2 \rfloor -1}\}$
of the rest
![]() $kn-1$
cards, which implies that
$kn-1$
cards, which implies that
![]() $R_{k,kn}$
is intransitive with
$R_{k,kn}$
is intransitive with
![]() $R_{k,kn}\leq C_2\wr S_{(kn-1)/2}$
. We have the following conjecture based on computation results.
$R_{k,kn}\leq C_2\wr S_{(kn-1)/2}$
. We have the following conjecture based on computation results.
Conjecture 5.3. Let
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $R_{k,kn}=\mathrm {Sh}(\langle \mathrm {Rev}(k)\rangle ,n)$
. Suppose that
$R_{k,kn}=\mathrm {Sh}(\langle \mathrm {Rev}(k)\rangle ,n)$
. Suppose that
![]() $kn$
is even and
$kn$
is even and
![]() $(k,n)\neq (\ell ^e,\ell ^f)$
for any positive integers
$(k,n)\neq (\ell ^e,\ell ^f)$
for any positive integers
![]() $\ell $
, e and f. Then the following hold:
$\ell $
, e and f. Then the following hold:
-
(a) If
 $(k,n)=(2,6)$
or
$(k,n)=(2,6)$
or
 $(6,2)$
, then
$(6,2)$
, then
 $R_{k,kn}=C_2^6\rtimes \mathrm {PGL}(2,5)$
.
$R_{k,kn}=C_2^6\rtimes \mathrm {PGL}(2,5)$
. -
(b) If
 $(k,n)=(3,4)$
, then
$(k,n)=(3,4)$
, then
 $R_{k,kn}=A_5$
.
$R_{k,kn}=A_5$
. -
(c) If
 $(k,n)=(4,3)$
, then
$(k,n)=(4,3)$
, then
 $R_{k,kn}=C_2\times A_5$
.
$R_{k,kn}=C_2\times A_5$
. -
(d) If
 $kn=24$
, then
$kn=24$
, then
 $R_{k,kn}=C_2^{11}\rtimes M_{12}$
.
$R_{k,kn}=C_2^{11}\rtimes M_{12}$
. -
(e) If
 $kn\neq 12$
,
$kn\neq 12$
,
 $k\equiv 2$
or
$k\equiv 2$
or
 $3\ \pmod {4}$
and
$3\ \pmod {4}$
and
 $n\equiv 2\ \pmod {4}$
, then
$n\equiv 2\ \pmod {4}$
, then
 $R_{k,kn}=C_2\wr S_{kn/2}$
.
$R_{k,kn}=C_2\wr S_{kn/2}$
. -
(f) If
 $k\equiv 2\ \pmod {4}$
and
$k\equiv 2\ \pmod {4}$
and
 $n\equiv 1\ \pmod {4}$
, then
$n\equiv 1\ \pmod {4}$
, then
 $R_{k,kn}=C_2^{ kn/2}\rtimes A_{ kn/2}$
.
$R_{k,kn}=C_2^{ kn/2}\rtimes A_{ kn/2}$
. -
(g) If
 $k\equiv 2\ \pmod {4}$
and
$k\equiv 2\ \pmod {4}$
and
 $n\equiv 3\ \pmod {4}$
, then
$n\equiv 3\ \pmod {4}$
, then
 $R_{k,kn}=C_2^{ (kn-2)/2}\rtimes S_{kn/2}$
.
$R_{k,kn}=C_2^{ (kn-2)/2}\rtimes S_{kn/2}$
. -
(h) Otherwise,
 $R_{k,kn}=C_2^{ (kn-2)/2}\rtimes A_{ kn/2}$
.
$R_{k,kn}=C_2^{ (kn-2)/2}\rtimes A_{ kn/2}$
.
Remark. Statements (a)–(d) have been verified by computation in Magma [Reference Bosma, Cannon and Playoust3], and we include them in Conjecture 5.3 for completeness. In fact, statement (d) is already mentioned in [Reference Medvedoff and Morrison13]. The reason why we assume
![]() $kn$
even and
$kn$
even and
![]() $(k,n)\neq (\ell ^e,\ell ^f)$
is that we have not yet identified the patterns of
$(k,n)\neq (\ell ^e,\ell ^f)$
is that we have not yet identified the patterns of
![]() $R_{k,kn}$
if
$R_{k,kn}$
if
![]() $kn$
is odd or
$kn$
is odd or
![]() $(k,n)= (\ell ^e,\ell ^f)$
for some positive integers
$(k,n)= (\ell ^e,\ell ^f)$
for some positive integers
![]() $\ell $
, e and f. However, we do have some interesting observations in special cases. For example, for
$\ell $
, e and f. However, we do have some interesting observations in special cases. For example, for
![]() $(k,n)=(\ell ^e,\ell ^f)$
with
$(k,n)=(\ell ^e,\ell ^f)$
with
![]() $\gcd (e,f)=1$
, it seems that
$\gcd (e,f)=1$
, it seems that
 $$ \begin{align} R_{k,kn}=\begin{cases} C_2^{e+f-1}\rtimes C_{e+f}&\ \text{ if }\ e\equiv f+1\equiv 0\quad\pmod{2}\\ C_2\wr C_{e+f}&\ \text{ otherwise}. \end{cases} \end{align} $$
$$ \begin{align} R_{k,kn}=\begin{cases} C_2^{e+f-1}\rtimes C_{e+f}&\ \text{ if }\ e\equiv f+1\equiv 0\quad\pmod{2}\\ C_2\wr C_{e+f}&\ \text{ otherwise}. \end{cases} \end{align} $$
This would be a generalisation of [Reference Amarra, Morgan and Praeger1, Theorem 1.4(1)], as the latter can be obtained from (14) by taking
![]() $e=1$
.
$e=1$
.
Finally, we would like to pose the following more challenging question.
Question 5.4. Given
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n\geq 1$
such that n is not a power of k and
$n\geq 1$
such that n is not a power of k and
![]() $(k,n)\neq (4,2^f)$
for any odd integer f, for what
$(k,n)\neq (4,2^f)$
for any odd integer f, for what
![]() $\theta \in \mathrm {Sym}([k])$
does
$\theta \in \mathrm {Sym}([k])$
does
![]() $\langle \sigma ,\rho _{\theta }\sigma \rangle =\mathrm {Sh}(\langle \theta \rangle ,n)$
contain
$\langle \sigma ,\rho _{\theta }\sigma \rangle =\mathrm {Sh}(\langle \theta \rangle ,n)$
contain
![]() $A_{kn}$
?
$A_{kn}$
?
Note that a complete answer to Question 5.4 would in particular solve Conjectures 5.1 and 5.3. Another interesting consequence would be the proportion
of valid permutations
![]() $\theta $
in
$\theta $
in
![]() $\mathrm {Sym}([k])$
for a pair
$\mathrm {Sym}([k])$
for a pair
![]() $(k,n)$
, especially when k and n are large. Our computation results suggest that this proportion is at least (for most cases much larger than)
$(k,n)$
, especially when k and n are large. Our computation results suggest that this proportion is at least (for most cases much larger than)
![]() $1/6$
.
$1/6$
.
Acknowledgements
The second author was supported by the Natural Science Foundation of Chongqing (CSTB2022NSCQ-MSX1054). The third author was supported by the Melbourne Research Scholarship provided by The University of Melbourne. The fourth author was supported by the China Scholarship Council (202106040068). The work was done during a visit of the fourth author to The University of Melbourne. The fourth author would like to thank The University of Melbourne for its hospitality and Beijing Normal University for consistent support. The authors wish to express their sincere gratitude to the anonymous referee for careful reading and invaluable suggestions to improve this paper.
Competing interest
The authors have no competing interest to declare.