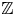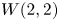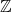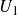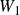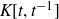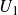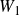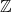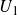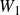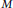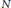Refine search
Actions for selected content:
13 results
Biderivations of Lie algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 440-450
- Print publication:
- June 2025
-
- Article
- Export citation
Classification of simple smooth modules over the Heisenberg–Virasoro algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1321-1365
- Print publication:
- August 2025
-
- Article
- Export citation
Classification of simple Harish–Chandra modules over the Ovsienko–Roger superalgebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 14 March 2023, pp. 483-493
- Print publication:
- April 2024
-
- Article
- Export citation
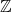 $\mathbb{Z}$-graded identities of the Lie algebras
$\mathbb{Z}$-graded identities of the Lie algebras 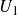 $U_1$ in characteristic 2
$U_1$ in characteristic 2
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2022, pp. 49-58
- Print publication:
- January 2023
-
- Article
- Export citation
ACTIONS OF MONOIDAL CATEGORIES AND REPRESENTATIONS OF CARTAN TYPE LIE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 2367-2402
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GROUP OF AUTOMORPHISMS OF THE LIE ALGEBRA OF DERIVATIONS OF A FIELD OF RATIONAL FUNCTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 513-524
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Sur les algèbres de Lie associées à une connexion
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 692-703
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Characterization of Simple Highest Weight Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 606-614
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE HARISH CHANDRA MODULES OVER THE DERIVATION ALGEBRAS OF RATIONAL QUANTUM TORI
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 677-693
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Jet Modules
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 712-729
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation
On the formal structure of logarithmic vector fields
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 17 May 2006, pp. 765-778
- Print publication:
- May 2006
-
- Article
-
- You have access
- Export citation
A New Class of Representations of EALA Coordinated by Quantum Tori in Two Variables
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 4 / 01 December 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 672-685
- Print publication:
- 01 December 2002
-
- Article
-
- You have access
- Export citation
Automorphisms of the Lie Algebras W * in Characteristic 0
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 1 / 01 February 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-132
- Print publication:
- 01 February 1997
-
- Article
-
- You have access
- Export citation