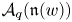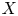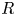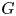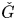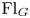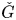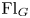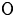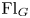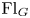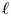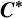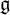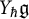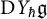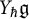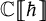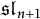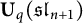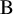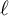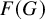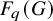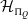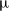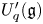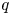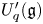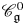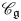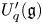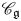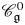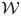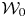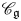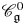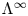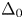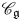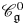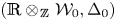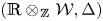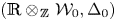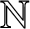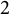Refine search
Actions for selected content:
65 results
Wreath Macdonald operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTEGRABLE MODULES OVER QUANTUM SYMMETRIC PAIR COIDEAL SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 2257-2282
- Print publication:
- November 2025
-
- Article
- Export citation
Gelfand–Tsetlin crystals
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 May 2025, pp. 1-14
-
- Article
- Export citation
Diagrammatics for the smallest quantum coideal and Jones–Wenzl projectors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-20
-
- Article
- Export citation
A comparison between
 $SL_n$ spider categories
$SL_n$ spider categories
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRESENTING INFINITESIMAL q-SCHUR ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 134-155
- Print publication:
- March 2025
-
- Article
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
Twisted Whittaker category on affine flags and the category of representations of the mixed quantum group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1349-1417
- Print publication:
- June 2024
-
- Article
- Export citation
SPHERICAL REPRESENTATIONS FOR
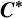 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 239-272
- Print publication:
- October 2024
-
- Article
- Export citation
The restricted quantum double of the Yangian
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 16 February 2024, pp. 770-841
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime representations in the Hernandez–Leclerc category: classical decompositions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1987-2018
- Print publication:
- December 2024
-
- Article
- Export citation
Comparison of quantizations of symmetric spaces: cyclotomic Knizhnik–Zamolodchikov equations and Letzter–Kolb coideals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE QUANTUM ISOMERIC SUPERCATEGORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1077-1124
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
A categorical approach to dynamical quantum groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A boson-fermion correspondence in cohomological Donaldson–Thomas theory
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 11 April 2022, pp. S28-S52
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SHUFFLE ALGEBRAS FOR QUIVERS AND R-MATRICES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 2583-2618
- Print publication:
- November 2023
-
- Article
- Export citation
Simply laced root systems arising from quantum affine algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 168-210
- Print publication:
- January 2022
-
- Article
- Export citation
Defining relations of quantum symmetric pair coideal subalgebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 05 October 2021, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation











 be a commutative ring containing a primitive
be a commutative ring containing a primitive 


 over
over  form an ascending chain of subalgebras of the
form an ascending chain of subalgebras of the  , which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let
, which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let  be the quantized enveloping algebra of
be the quantized enveloping algebra of 
 . There is a natural surjective algebra homomorphism
. There is a natural surjective algebra homomorphism 
 to
to  . The map
. The map 

 to
to  , where
, where  is a certain Hopf subalgebra of
is a certain Hopf subalgebra of  , which is closely related to Frobenius–Lusztig kernels of
, which is closely related to Frobenius–Lusztig kernels of  . We give the extra defining relations needed to define the infinitesimal
. We give the extra defining relations needed to define the infinitesimal  as a quotient of
as a quotient of  . The map
. The map 
 , where
, where  is the modified quantum algebra associated with
is the modified quantum algebra associated with  . We also give a generating set for the kernel of
. We also give a generating set for the kernel of 
 -modules over a field of characteristic
-modules over a field of characteristic