Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-22T20:32:38.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Simply laced root systems arising from quantum affine algebras

Part of: Modules, bimodules and ideals Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  08 February 2022

Masaki Kashiwara ,
Myungho Kim ,
Se-jin Oh  and
Euiyong Park
Masaki Kashiwara
Affiliation:
Kyoto University Institute for Advanced Study, Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan masaki@kurims.kyoto-u.ac.jp Korea Institute for Advanced Study, Seoul 02455, Korea
Myungho Kim
Affiliation:
Department of Mathematics, Kyung Hee University, Seoul 02447, Korea mkim@khu.ac.kr
Se-jin Oh
Affiliation:
Department of Mathematics, Ewha Womans University, Seoul 03760, Korea sejin092@gmail.com
Euiyong Park
Affiliation:
Department of Mathematics, University of Seoul, Seoul 02504, Korea epark@uos.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 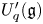$U_q'({\mathfrak {g}})$ be a quantum affine algebra with an indeterminate 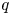$q$, and let 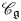$\mathscr {C}_{\mathfrak {g}}$ be the category of finite-dimensional integrable 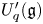$U_q'({\mathfrak {g}})$-modules. We write 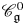$\mathscr {C}_{\mathfrak {g}}^0$ for the monoidal subcategory of 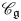$\mathscr {C}_{\mathfrak {g}}$ introduced by Hernandez and Leclerc. In this paper, we associate a simply laced finite-type root system to each quantum affine algebra 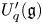$U_q'({\mathfrak {g}})$ in a natural way and show that the block decompositions of 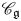$\mathscr {C}_{\mathfrak {g}}$ and 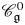$\mathscr {C}_{\mathfrak {g}}^0$ are parameterized by the lattices associated with the root system. We first define a certain abelian group 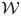$\mathcal {W}$ (respectively 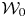$\mathcal {W} _0$) arising from simple modules of 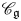$\mathscr {C}_{\mathfrak {g}}$ (respectively 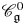$\mathscr {C}_{\mathfrak {g}}^0$) by using the invariant 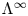$\Lambda ^\infty$ introduced in previous work by the authors. 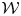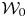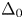The groups $\mathcal {W}$ and $\mathcal {W} _0$ have subsets $\Delta$ and $\Delta _0$ determined by the fundamental representations in 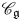$\mathscr {C}_{\mathfrak {g}}$ and 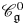$\mathscr {C}_{\mathfrak {g}}^0$, respectively. We prove that the pair 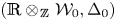$( \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} _0, \Delta _0)$ is an irreducible simply laced root system of finite type and that the pair 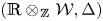$( \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} , \Delta )$ is isomorphic to the direct sum of infinite copies of 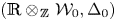$( \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} _0, \Delta _0)$ as a root system.

Keywords

block decompositionquantum affine algebrasR-matricesroot systems

MSC classification

Primary: 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 1 , January 2022 , pp. 168 - 210
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research of M. Kashiwara was supported by Grant-in-Aid for Scientific Research (B) 20H01795 from the Japan Society for the Promotion of Science.

The research of M. Kim was supported by a National Research Foundation (NRF) grant funded by the government of Korea (MSIP) (NRF-2017R1C1B2007824 and NRF-2020R1A5A1016126).

The research of S.-J.O. was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2019R1A2C4069647).

The research of E.P. was supported by a National Research Foundation (NRF) grant funded by the government of Korea (MSIP)(NRF-2020R1F1A1A01065992 and NRF-2020R1A5A1016126).

References

Akasaka, T. and Kashiwara, M., Finite-dimensional representations of quantum affine algebras, Publ. RIMS Kyoto Univ. 33 (1997), 839–867.CrossRefGoogle Scholar
Chari, V., Braid group actions and tensor products, Int. Math. Res. Not. IMRN 2002 (2010), 357–382.CrossRefGoogle Scholar
Chari, V. and Moura, A. A., Spectral characters of finite-dimensional representations of affine algebras, J. Algebra 279 (2004), 820–839.CrossRefGoogle Scholar
Chari, V. and Moura, A. A., Characters and blocks for finite-dimensional representations of quantum affine algebras, Int. Math. Res. Not. IMRN 5 (2005), 257–298.CrossRefGoogle Scholar
Chari, V. and Pressley, A., A guide to quantum groups (Cambridge University Press, Cambridge, 1994).Google Scholar
Date, E. and Okado, M., Calculation of excitation spectra of the spin model related with the vector representation of the quantized affine algebra of type $A^{(1)}_n$, Internat. J. Modern Phys. A 9 (1994), 399–417.CrossRefGoogle Scholar
Drinfel'd, V. G., Quantum groups, in Proc. int. cong. math., vol. 1 and 2, Berkeley, CA, 1986 (American Mathematical Society, Providence, RI, 1987), 798–820.Google Scholar
Etingof, P. and Moura, A. A., Elliptic central characters and blocks of finite dimensional representations of quantum affine algebras, Represent. Theory 7 (2003), 346–373.CrossRefGoogle Scholar
Frenkel, E. and Hernandez, D., Langlands duality for representations of quantum groups, Math. Ann. 349 (2011), 705–746.CrossRefGoogle Scholar
Frenkel, E. and Hernandez, D., Langlands duality for finite-dimensional representations of quantum affine algebras, Lett. Math. Phys. 96 (2011), 217–261.CrossRefGoogle Scholar
Frenkel, E. and Reshetikhin, N., Deformations of $W$-algebras associated to simple Lie algebras, Comm. Math. Phys. 197 (1998), 1–32.Google Scholar
Frenkel, E. and Reshetikhin, N., The q-characters of representations of quantum affine algebras and deformations of W-algebras, recent developments in quantum affine algebras and related topics, Contemp. Math. 248 (1999), 163–205.CrossRefGoogle Scholar
Fujita, R., Geometric realization of Dynkin quiver type quantum affine Schur–Weyl duality, Int. Math. Res. Not. IMRN 22 (2020), 8353–8386.Google Scholar
Fujita, R., Graded quiver varieties and singularities of normalized R-matrices for fundamental modules, Selecta Math. (N.S.) 28(1) (2022), Paper no. 2.CrossRefGoogle Scholar
Fujita, R., Hernandez, D., Oh, S.-J. and Oya, H., Isomorphisms among quantum Grothendieck rings and propagation of positivity, Preprint (2021), arXiv:2101.07489v2.Google Scholar
Fujita, R. and Oh, S.-J., $Q$-data and representation theory of untwisted quantum affine algebras, Comm. Math. Phys. 384 (2021), 1351–1407.CrossRefGoogle Scholar
Hernandez, D. and Leclerc, B., Cluster algebras and quantum affine algebras, Duke Math. J. 154 (2010), 265–341.CrossRefGoogle Scholar
Hernandez, D. and Leclerc, B., Quantum Grothendieck ring and derived Hall algebras, J. Reine Angew. Math. 701 (2015), 77–126.CrossRefGoogle Scholar
Hernandez, D. and Leclerc, B., A cluster algebra approach to q-characters of Kirillov-Reshetikhin modules, J. Eur. Math. Soc. 18 (2016), 1113–1159.CrossRefGoogle Scholar
Jakelić, D. and Moura, A. A., Tensor products, characters, and blocks of finite-dimensional representations of quantum affine algebras at roots of unity, Int. Math. Res. Not. IMRN 18 (2011), 4147–4199.Google Scholar
Kac, V., Infinite dimensional lie algebras, third edition (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M. and Kim, M., Symmetric quiver Hecke algebras and $R$-matrices of quantum affine algebras II, Duke Math. J. 164 (2015), 1549–1602.CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M., Kim, M. and Oh, S.-J., Simplicity of heads and socles of tensor products, Compos. Math. 151 (2015), 377–396.CrossRefGoogle Scholar
Kang, S.-J., Kashiwara, M., Kim, M. and Oh, S.-J., Symmetric quiver Hecke algebras and R-matrices of quantum affine algebras IV, Selecta Math. (N.S.) 22 (2016), 1987–2015.CrossRefGoogle Scholar
Kashiwara, M., On level zero representations of quantum affine algebras, Duke Math. J. 112 (2002), 117–175.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-J. and Park, E., Monoidal categorification and quantum affine algebras, Compos. Math. 156 (2020), 1039–1077.CrossRefGoogle Scholar
Kashiwara, M., Kim, M., Oh, S.-J. and Park, E., Monoidal categorification and quantum affine algebras II, Preprint (2021), arXiv:2103.10067v1.Google Scholar
Kashiwara, M. and Oh, S.-J., Categorical relations between Langlands dual quantum affine algebras: doubly laced types, J. Algebraic Combin. 49 (2019), 401–435.CrossRefGoogle Scholar
Lusztig, G., Quantum groups at roots of 1, Geom. Dedicata 35 (1990), 89–11.CrossRefGoogle Scholar
Nakajima, H., Quiver varieties and finite-dimensional representations of quantum affine algebras, J. Amer. Math. Soc. 14 (2001), 145–238.CrossRefGoogle Scholar
Oh, S.-J., The denominators of normalized R-matrices of types $A^{(2)}_{2n-1}$, $A^{(2)}_{2n}$, $B^{(1)}_n$ and $D^{(2)}_{n+1}$, Publ. RIMS Kyoto Univ. 51 (2015), 709–744.CrossRefGoogle Scholar
Oh, S.-J. and Scrimshaw, T., Categorical relations between Langlands dual quantum affine algebras: exceptional cases, Comm. Math. Phys. 368 (2019), 295–367.CrossRefGoogle Scholar
Oh, S.-J. and Suh, U., Twisted and folded Auslander-Reiten quiver and applications to the representation theory of quantum affine algebras, J. Algebra 535 (2019), 53–132.Google Scholar
Saito, Y., PBW basis of quantized universal enveloping algebras, Publ. Res. Inst. Math. Sci. 30 (1994), 209–232.CrossRefGoogle Scholar
Senesi, P., The block decomposition of finite-dimensional representations of twisted loop algebras, Pacific J. Math. 244 (2010), 335–357.CrossRefGoogle Scholar