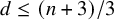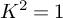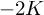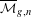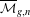Refine search
Actions for selected content:
17 results
A GEOMETRIC APPROACH TO POLYNOMIAL PROPERTY FOR PATTERN SUBGROUPS IN
 ${{\mathrm {\mathbf {U}}}}_{\boldsymbol {a,b,c,d}}$
${{\mathrm {\mathbf {U}}}}_{\boldsymbol {a,b,c,d}}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-18
-
- Article
- Export citation
Torsion points and concurrent exceptional curves on del Pezzo surfaces of degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 634-652
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GV and GW invariants via the enhanced movable cone
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Genus-zero r-spin theory
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the asymptotic enumerativity property for Fano manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Avoidance loci and tropicalizations of real bitangents to plane quartics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 July 2023, pp. 1308-1312
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Floor diagrams and enumerative invariants of line bundles over an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. 1741-1790
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some hyperelliptic Hurwitz–Hodge integrals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 271-284
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Level correspondence of the K-theoretic I-function in Grassmann duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 June 2022, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINED COUNT OF REAL RATIONAL CURVES OF CANONICAL DEGREE 2 ON REAL DEL PEZZO SURFACES WITH
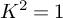 $K^2=1$
$K^2=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 14 June 2022, pp. 123-148
- Print publication:
- January 2024
-
- Article
- Export citation
THE MODULI SPACE OF TWISTED CANONICAL DIVISORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 05 April 2016, pp. 615-672
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Rational functions with given ramification in characteristic p
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 13 March 2006, pp. 433-450
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Degeneracy of 2-Forms and 3-Forms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 4 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-560
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
geometry on nodal curves
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 5 / September 2005
- Published online by Cambridge University Press:
- 01 September 2005, pp. 1191-1212
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
The Characteristic Numbers of Quartic Plane Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 5 / 01 October 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1089-1120
- Print publication:
- 01 October 1999
-
- Article
-
- You have access
- Export citation
On the Dual of Projective Varieties
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 4 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 433-439
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation