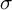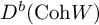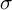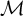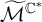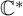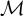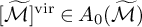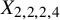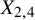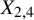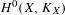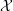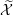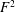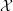Refine search
Actions for selected content:
41 results
Mirror symmetry for log Calabi–Yau surfaces II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 22 October 2025, pp. 2025-2090
- Print publication:
- August 2025
-
- Article
- Export citation
Smoothing, scattering and a conjecture of Fukaya
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A cone conjecture for log Calabi-Yau surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of Calabi–Yau varieties with k-liminal singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Attractors are not algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1073-1100
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nef cones of fiber products and an application to the cone conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 March 2024, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal log discrepancies of hypersurface mirrors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 19 February 2024, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some examples of noncommutative projective Calabi–Yau schemes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 706-726
- Print publication:
- September 2024
-
- Article
- Export citation
INTRINSIC STABILIZER REDUCTION AND GENERALIZED DONALDSON–THOMAS INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1987-2025
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Second-order estimates for collapsed limits of Ricci-flat Kähler metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 912-926
- Print publication:
- September 2023
-
- Article
- Export citation
Stability condition on Calabi–Yau threefold of complete intersection of quadratic and quartic hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 December 2022, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On genus one mirror symmetry in higher dimensions and the BCOV conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirror symmetry and automorphisms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smoothing toroidal crossing spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 August 2021, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birational boundedness of low-dimensional elliptic Calabi–Yau varieties with a section
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 21 July 2021, pp. 1766-1806
- Print publication:
- August 2021
-
- Article
- Export citation
Smoothing Calabi–Yau toric hypersurfaces using the Gross–Siebert algorithm
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 17 June 2021, pp. 1441-1491
- Print publication:
- July 2021
-
- Article
- Export citation
Tropically constructed Lagrangians in mirror quintic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e58
-
- Article
-
- You have access
- Open access
- Export citation
Global geometry on moduli of local systems for surfaces with boundary
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1517-1559
- Print publication:
- August 2020
-
- Article
- Export citation
THE INTEGRAL HODGE CONJECTURE FOR 3-FOLDS OF KODAIRA DIMENSION ZERO
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 February 2020, pp. 1697-1717
- Print publication:
- September 2021
-
- Article
- Export citation
Variation of Mixed Hodge Structures Associated to an Equisingular One-dimensional Family of Calabi-Yau Threefolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 441-464
- Print publication:
- April 2021
-
- Article
- Export citation










 introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part
introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part