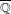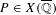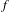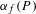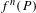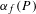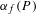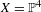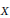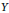Refine search
Actions for selected content:
30 results
Maximal subgroups in the Cremona group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 November 2025, pp. 2442-2460
- Print publication:
- September 2025
-
- Article
- Export citation
Finite groups of symplectic birational transformations of IHS manifolds of
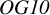 $\mathit {OG10}$ type
$\mathit {OG10}$ type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant geometry of singular cubic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birationally rigid Fano-Mori fibre spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
O’Grady tenfolds as moduli spaces of sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois points and Cremona transformations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 471-478
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
Higher index Fano varieties with finitely many birational automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 02 December 2022, pp. 2033-2045
- Print publication:
- November 2022
-
- Article
- Export citation
TORSORS AND STABLE EQUIVARIANT BIRATIONAL GEOMETRY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 275-297
- Print publication:
- June 2023
-
- Article
- Export citation
THE EMBEDDINGS OF THE HEISENBERG GROUP INTO THE CREMONA GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 243-251
- Print publication:
- January 2022
-
- Article
- Export citation
Some effectivity questions for plane Cremona transformations in the context of symmetric key cryptography
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 1-28
-
- Article
- Export citation
A rational map with infinitely many points of distinct arithmetic degrees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 12 April 2019, pp. 3051-3055
- Print publication:
- November 2020
-
- Article
- Export citation
Super-rigid affine Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 17 October 2018, pp. 2462-2484
- Print publication:
- November 2018
-
- Article
- Export citation
Birationally Rigid Complete Intersections with a Singular Point of High Multiplicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 26 September 2018, pp. 221-239
-
- Article
- Export citation
Cremona transformations and derived equivalences of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 28 May 2018, pp. 1508-1533
- Print publication:
- July 2018
-
- Article
-
- You have access
- HTML
- Export citation
The Hodge diamond of O’Grady’s six-dimensional example
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 21 March 2018, pp. 984-1013
- Print publication:
- May 2018
-
- Article
- Export citation
ON CONJUGACY CLASSES OF THE KLEIN SIMPLE GROUP IN CREMONA GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 395-400
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
Strongly Incompressible Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 3 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 541-570
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
Circle of Sarkisov Links on a Fano 3-Fold
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 May 2016, pp. 1-16
-
- Article
- Export citation
Homaloidal nets and ideals of fat points I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 54-77
-
- Article
-
- You have access
- Export citation


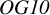
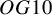
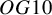
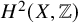
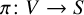
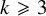
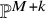
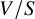
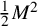
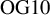
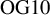
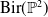
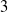
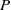
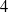
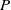
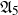
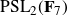
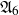
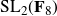
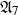
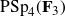
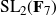
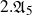
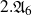
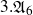
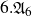
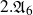
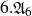
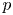
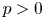
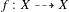 be a dominant rational self-map of a smooth projective variety defined over
be a dominant rational self-map of a smooth projective variety defined over