Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Matsumura, Shin-ichi
2015.
A Nadel vanishing theorem for metrics with minimal singularities on big line bundles.
Advances in Mathematics,
Vol. 280,
Issue. ,
p.
188.
Lehmann, Brian
2015.
Numerical triviality and pullbacks.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 12,
p.
5637.
Muñoz, Roberto
Di Sciullo, Fulvio
and
Solá Conde, Luis E.
2015.
On the existence of a weak Zariski decomposition on projectivized vector bundles.
Geometriae Dedicata,
Vol. 179,
Issue. 1,
p.
287.
Lesieutre, John
and
Ottem, John Christian
2016.
Curves disjoint from a nef divisor.
Michigan Mathematical Journal,
Vol. 65,
Issue. 2,
Choi, Sung Rak
and
Park, Jinhyung
2016.
Potentially non-klt locus and its applications.
Mathematische Annalen,
Vol. 366,
Issue. 1-2,
p.
141.
Graf, Patrick
2016.
A Mehta-Ramanathan theorem for linear systems with basepoints.
Mathematische Nachrichten,
Vol. 289,
Issue. 10,
p.
1208.
Küronya, Alex
and
Lozovanu, Victor
2017.
Infinitesimal Newton–Okounkov bodies and jet separation.
Duke Mathematical Journal,
Vol. 166,
Issue. 7,
Mistretta, Ernesto C
and
Urbinati, Stefano
2019.
Iitaka Fibrations for Vector Bundles.
International Mathematics Research Notices,
Vol. 2019,
Issue. 7,
p.
2223.
Montero, Pedro
2019.
Newton–Okounkov bodies on projective bundles over curves.
Mathematische Zeitschrift,
Vol. 291,
Issue. 3-4,
p.
1357.
Keeler, Dennis
2020.
Arithmetically Nef Line Bundles.
Michigan Mathematical Journal,
Vol. 69,
Issue. 3,
Misra, Snehajit
2021.
Pseudo-effective cones of projective bundles and weak Zariski decomposition.
European Journal of Mathematics,
Vol. 7,
Issue. 4,
p.
1438.
Han, Jingjun
and
Li, Zhan
2022.
Weak Zariski decompositions and log terminal models for generalized pairs.
Mathematische Zeitschrift,
Vol. 302,
Issue. 2,
p.
707.
Choi, Sung Rak
and
Gongyo, Yoshinori
2022.
On a generalized Batyrev’s cone conjecture.
Mathematische Zeitschrift,
Vol. 300,
Issue. 2,
p.
1319.
Collins, Tristan C.
and
Tosatti, Valentino
2022.
Restricted volumes on Kähler manifolds.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 31,
Issue. 3,
p.
907.
Chang, Chi-Kang
2023.
Positivity of anticanonical divisors in algebraic fibre spaces.
Mathematische Annalen,
Vol. 385,
Issue. 1-2,
p.
787.
Dumitrescu, Olivia
and
Miranda, Rick
2024.
On (i)-Curves in Blowups of Pr.
Mathematics,
Vol. 12,
Issue. 24,
p.
3952.
Boucksom, Sébastien
and
Jonsson, Mattias
2024.
Non-Archimedean Green’s functions and Zariski decompositions.
Comptes Rendus. Mathématique,
Vol. 362,
Issue. S1,
p.
5.
Choi, Sung Rak
Jang, Sungwook
and
Lee, Dae-Won
2025.
On Minimal Model Program and Zariski Decomposition of Potential Triples.
Taiwanese Journal of Mathematics,
Vol. 29,
Issue. 6,
Mistretta, Ernesto C.
2025.
Moduli, Motives and Bundles.
p.
406.
Hashizume, Kenta
2025.
Minimal Model Program for Normal Pairs along log Canonical Locus.
Forum of Mathematics, Sigma,
Vol. 13,
Issue. ,
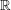 $\mathbb{R}$-divisor
$\mathbb{R}$-divisor 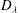 ${D}_{\lambda }$ on the blow-up of
${D}_{\lambda }$ on the blow-up of 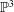 ${\mathbb{P}}^{3}$ at nine very general points which lies in the closed movable cone and has negative intersections with a set of curves whose union is Zariski dense. It follows that the diminished base locus
${\mathbb{P}}^{3}$ at nine very general points which lies in the closed movable cone and has negative intersections with a set of curves whose union is Zariski dense. It follows that the diminished base locus 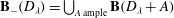 ${\boldsymbol{B}}_{-}({D}_{\lambda })={\bigcup }_{A\,\text{ample}}\boldsymbol{B}({D}_{\lambda }+A)$ is not closed and that
${\boldsymbol{B}}_{-}({D}_{\lambda })={\bigcup }_{A\,\text{ample}}\boldsymbol{B}({D}_{\lambda }+A)$ is not closed and that 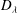 ${D}_{\lambda }$ does not admit a Zariski decomposition in even a very weak sense. By a similar method, we construct an
${D}_{\lambda }$ does not admit a Zariski decomposition in even a very weak sense. By a similar method, we construct an 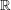 $\mathbb{R}$-divisor on the family of blow-ups of
$\mathbb{R}$-divisor on the family of blow-ups of 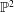 ${\mathbb{P}}^{2}$ at ten distinct points, which is nef on a very general fiber but fails to be nef over countably many prime divisors in the base.
${\mathbb{P}}^{2}$ at ten distinct points, which is nef on a very general fiber but fails to be nef over countably many prime divisors in the base.
