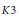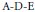Refine search
Actions for selected content:
17 results
Equivariant vector bundles on toric schemes over semirings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
On the strict Picard spectrum of commutative ring spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1872-1897
- Print publication:
- September 2023
-
- Article
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the effective, nef, and semi-ample monoids of blowups of Hirzebruch surfaces at collinear points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1179-1193
- Print publication:
- December 2023
-
- Article
- Export citation
Line bundles on rigid spaces in the v-topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 September 2022, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE POSITION OF NODES OF PLANE CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 62-68
- Print publication:
- February 2021
-
- Article
- Export citation
EPSILON-STRONGLY GROUPOID-GRADED RINGS, THE PICARD INVERSE CATEGORY AND COHOMOLOGY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 233-259
- Print publication:
- January 2020
-
- Article
-
- You have access
- Open access
- Export citation
Picard groups of higher real
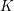 $K$ -theory spectra at height
$K$ -theory spectra at height 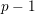 $p-1$
$p-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1820-1854
- Print publication:
- September 2017
-
- Article
- Export citation
Construction of automorphisms of hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1610-1621
- Print publication:
- August 2017
-
- Article
- Export citation
DYNAMICS ON SUPERSINGULAR K3 SURFACES AND AUTOMORPHISMS OF SALEM DEGREE 22
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-15
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
Elliptic Fibrations on K3 Surfaces
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 253-267
-
- Article
-
- You have access
- Export citation
A Noether-Lefschetz theorem for varieties of r-planes in complete intersections
-
- Journal:
- Nagoya Mathematical Journal / Volume 206 / June 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 39-66
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
COMPUTATION OF THE GROTHENDIECK AND PICARD GROUPS OF A TORIC DM STACK
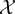 BY USING A HOMOGENEOUS COORDINATE RING FOR
BY USING A HOMOGENEOUS COORDINATE RING FOR 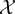
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 01 September 2010, pp. 97-113
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Group Actions, Cyclic Coverings and Families of K3-Surfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 4 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 592-608
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
Stacks of cyclic covers of projective spaces
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 647-666
- Print publication:
- May 2004
-
- Article
-
- You have access
- Export citation

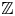
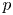
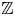
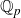
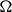
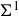
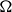
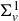
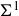
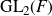
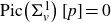
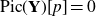
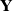
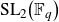
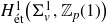
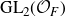
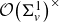
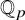
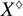
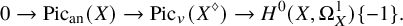
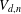
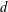

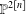
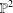

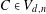

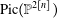
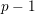
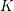
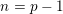
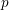
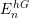
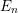
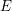
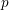
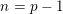
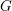
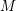
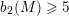
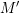
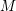
 BY USING A HOMOGENEOUS COORDINATE RING FOR
BY USING A HOMOGENEOUS COORDINATE RING FOR