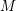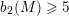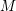Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ouchi, Genki
2018.
Automorphisms of positive entropy on some hyperKähler manifolds via derived automorphisms of K3 surfaces.
Advances in Mathematics,
Vol. 335,
Issue. ,
p.
1.
Brandhorst, Simon
2020.
On the stable dynamical spectrum of complex surfaces.
Mathematische Annalen,
Vol. 377,
Issue. 1-2,
p.
421.
Lesieutre, John
and
Satriano, Matthew
2021.
Canonical Heights on Hyper-Kähler Varieties and the Kawaguchi–Silverman Conjecture.
International Mathematics Research Notices,
Vol. 2021,
Issue. 10,
p.
7677.
Amerik, Ekaterina
and
Verbitsky, Misha
2023.
Parabolic automorphisms of hyperkähler manifolds.
Journal de Mathématiques Pures et Appliquées,
Vol. 179,
Issue. ,
p.
232.
Fino, Anna
Grantcharov, Gueo
and
Verbitsky, Misha
2025.
Special Hermitian structures on suspensions.
Mathematische Annalen,
Vol. 392,
Issue. 1,
p.
1099.