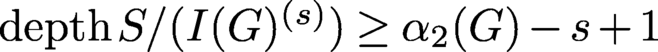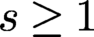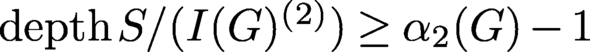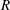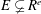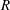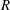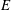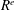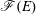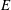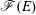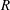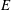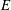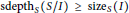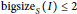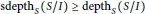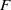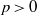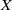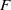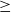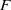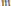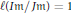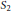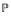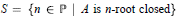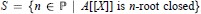Refine search
Actions for selected content:
20 results
Embedding codimension of the space of arcs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 February 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DEPTH OF SYMBOLIC POWERS OF EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 28-40
- Print publication:
- March 2022
-
- Article
- Export citation
SYMBOLIC ANALYTIC SPREAD: UPPER BOUNDS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 07 May 2020, pp. 1969-1981
- Print publication:
- November 2021
-
- Article
- Export citation
On the Ideal Case of a Conjecture of Huneke and Wiegand
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 847-859
-
- Article
- Export citation
On Special Fiber Rings of Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 225-242
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
NONINCREASING DEPTH FUNCTIONS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 505-511
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
NONNOETHERIAN HOMOTOPY DIMER ALGEBRAS AND NONCOMMUTATIVE CREPANT RESOLUTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 447-479
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 14 March 2017, pp. 705-715
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
On Stanley Depths of Certain Monomial Factor Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 393-401
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
The binomial edge ideal of a pair of graphs
-
- Journal:
- Nagoya Mathematical Journal / Volume 213 / March 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 105-125
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Depth of
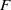 $F$-singularities and base change of relative canonical sheaves
$F$-singularities and base change of relative canonical sheaves
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 05 March 2013, pp. 43-63
- Print publication:
- January 2014
-
- Article
- Export citation
Cohen-Macaulay binomial edge ideals
-
- Journal:
- Nagoya Mathematical Journal / Volume 204 / December 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 57-68
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
On Fiber Cones of
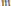 $\text{m}$ -Primary Ideals
$\text{m}$ -Primary Ideals
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 1 / 01 February 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-126
- Print publication:
- 01 February 2007
-
- Article
-
- You have access
- Export citation
Fiber Cones of Ideals with Almost Minimal Multiplicity
-
- Journal:
- Nagoya Mathematical Journal / Volume 177 / 2005
- Published online by Cambridge University Press:
- 11 January 2016, pp. 155-179
- Print publication:
- 2005
-
- Article
-
- You have access
- Export citation
The transcendence degree of an integral domain over a subfield and the dimension of the domain
-
- Journal:
- Nagoya Mathematical Journal / Volume 170 / 2003
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-162
- Print publication:
- 2003
-
- Article
-
- You have access
- Export citation
The Grade Conjecture and the S 2 Condition
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 1 / 01 March 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
- Print publication:
- 01 March 2002
-
- Article
-
- You have access
- Export citation
On the dimension and multiplicity of local cohomology modules
-
- Journal:
- Nagoya Mathematical Journal / Volume 167 / 2002
- Published online by Cambridge University Press:
- 22 January 2016, pp. 217-233
- Print publication:
- 2002
-
- Article
-
- You have access
- Export citation
On the Prime Ideals in a Commutative Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-319
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
Root Closure in Integral Domains, III
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-9
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation
On t- Spec(R[[X]])
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 2 / 01 June 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 187-195
- Print publication:
- 01 June 1995
-
- Article
-
- You have access
- Export citation