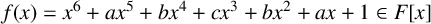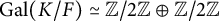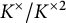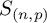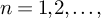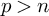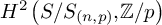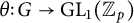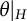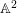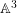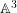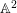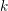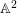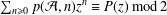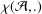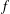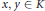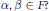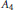Refine search
Actions for selected content:
34 results
AN EFFECTIVE VERSION OF THE PRIMITIVE ELEMENT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-8
-
- Article
- Export citation
Motivic versions of mass formulas by Krasner, Serre and Bhargava
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE TRIVIALITY OF AN
 $\mathbb A^2$-FIBRATION OVER A DVR
$\mathbb A^2$-FIBRATION OVER A DVR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 826-832
- Print publication:
- December 2025
-
- Article
- Export citation
KRONECKER CLASSES, NORMAL COVERINGS AND CHIEF FACTORS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 458-472
- Print publication:
- December 2025
-
- Article
- Export citation
On ρ-conjugate Hopf–Galois structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 288-304
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS GROUPS OF RECIPROCAL SEXTIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 37-44
- Print publication:
- February 2024
-
- Article
- Export citation
Galois module structure of square power classes for biquadratic extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 804-827
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ZASSENHAUS FILTRATION OF A FREE PROFINITE GROUP AND SHUFFLE RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 961-983
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois-theoretic features for 1-smooth pro-p groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 525-541
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the degree of repeated radical extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 877-885
- Print publication:
- December 2021
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
APPLICATIONS OF SYSTEMS OF QUADRATIC FORMS TO GENERALISED QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 374-386
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Galois Groups of Even Sextic Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 670-676
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
ON SEPARABLE
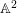 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 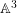 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 346-354
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
GEOMETRIC REPRESENTATION IN THE THEORY OF PSEUDO-FINITE FIELDS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1132-1139
- Print publication:
- September 2017
-
- Article
- Export citation
SETS WITH EVEN PARTITION FUNCTIONS AND CYCLOTOMIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 289-302
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
On the Theorem of the Primitive Element with Applications to the Representation Theory of Associative and Lie Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 735-748
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Infinite Families of A4-Sextic Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 538-545
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
FINITE GROUPS AS GALOIS GROUPS OF FUNCTION FIELDS WITH INFINITE FIELD OF CONSTANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 14 May 2010, pp. 301-312
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation