No CrossRef data available.
Article contents
On the degree of repeated radical extensions
Published online by Cambridge University Press: 23 November 2020
Abstract
We answer a question posed by Mordell in 1953, in the case of repeated radical extensions, and find necessary and sufficient conditions for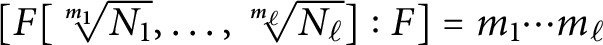 
$[F[\sqrt [m_1]{N_1},\dots ,\sqrt [m_\ell ]{N_\ell }]:F]=m_1\cdots m_\ell $, where F is an arbitrary field of characteristic not dividing any 
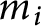$m_i$.
MSC classification
Primary:
12F05: Algebraic extensions
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
This paper is dedicated to Natalio H. Guersenzvaig. This research was partially supported by an NSERC grant.
References
Albu, T.,
Kummer extensions with few roots of unity
. J. Number Theory 41(1992), 322–358. https://doi.org/10.1016/0022-314X(9)90131-8
CrossRefGoogle Scholar
Besicovitch, A. S.,
On the linear independence of fractional powers of integers
. J. Lond. Math. Soc. 15(1940) 3–6. https://doi.org/10.1112/jlms/s1-15.1.3
CrossRefGoogle Scholar
Cagliero, L. and Szechtman, F.,
On the theorem of the primitive element with applications to the representation theory of associative and Lie algebras
. Canad. Math. Bull. 57(2014), 735–748. https://doi.org/10.4153/CMB-2013-046-9
CrossRefGoogle Scholar
Capelli, A.,
Sulla riduttibilitá delle equazioni algebriche. Nota prima. Rend. Accad. Sci. Fis. Mat. Soc. Napoli 3(1897), 243–252.Google Scholar
Carr, R. and O’Sullivan, C.,
On the linear independence of roots
. Int. J. Number Theory 5(2009), 161–171. https://doi.org/10.1142/S1793042109002018
CrossRefGoogle Scholar
Diviš, B.,
On the degrees of the sum and product of two algebraic elements
. In: Number theory and algebra, Academic Press, New York, 1977, pp. 19–27.Google Scholar
Flanders, H.,
Advanced problems and solutions: Solutions 4797
. Amer. Math Monthly 67(1960), 188–189.Google Scholar
Hasse, H.,
Klasssenkörpertheorie
. Mimeographed lectures, Marburg, 1932–33, pp. 187–195.Google Scholar
Isaacs, I. M.,
Degrees of sums in a separable field extension
. Proc. Amer. Math. Soc. 25(1970), 638–641. https://doi.org/10.2307/2036661
CrossRefGoogle Scholar
Mordell, L. J.,
On the linear independence of algebraic numbers
. Pacific J. Math. 3(1953), 625–630.CrossRefGoogle Scholar
Richards, I.,
An application of Galois theory to elementary arithmetic
. Adv. in Math. 13(1974) 268–273. https://doi.org/10.1016/0001-8708(74)90070-X
CrossRefGoogle Scholar
Roth, R. L., On extension of
$\mathbb{Q}$
by square roots. Amer. Math Monthly 78(1971), 392–393. https://doi.org/10.2307/2316910
CrossRefGoogle Scholar
$\mathbb{Q}$
by square roots. Amer. Math Monthly 78(1971), 392–393. https://doi.org/10.2307/2316910
CrossRefGoogle ScholarSiegel, C. L.,
Algebraische Abhängigkeit von Wurzein
. Acta Arith. 21(1972), 59–64. https://doi.org/10.4064/aa-21-1-59-64
CrossRefGoogle Scholar
Ursell, H. D.,
The degree of radical extensions
. Canad. Math. Bull. 17(1974), 615–617. https://doi.org/10.4153/CMB-1974-114-x
CrossRefGoogle Scholar
Vahlen, K. T.,
Über reductible Binome
. Acta Math. 19(1895), 195–198. https://doi.org/10.1007/BF02402875
CrossRefGoogle Scholar
Zhou, J.-P.,
On the degree of extensions generated by finitely many algebraic numbers
. J. Number Theory 34(1990), 133–141. https://doi.org/10.1016/0022-314X(90)90144-G
Google Scholar