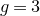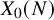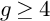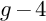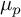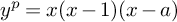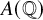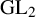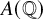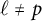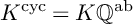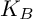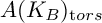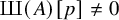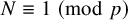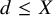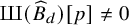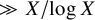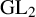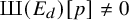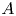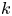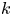Refine search
Actions for selected content:
89 results
Anisotropic area-preserving flows for plane curves and entropy inequalities
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 September 2025, pp. 1-25
-
- Article
- Export citation
HODGE CYCLES AND QUADRATIC RELATIONS BETWEEN HOLOMORPHIC PERIODS ON CM ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On (2,2)-decomposable genus 4 Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOMBRE DE PETITS POINTS SUR UNE VARIÉTÉ ABÉLIENNE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 705-761
- Print publication:
- May 2025
-
- Article
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete verification of strong BSD for many modular abelian surfaces over
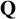 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The isotrivial case in the Mordell-Lang conjecture for semiabelian varieties defined over fields of positive characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 461-476
- Print publication:
- June 2025
-
- Article
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational torsion points on abelian surfaces with quaternionic multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computing the Cassels–Tate pairing for genus two jacobians with rational two-torsion points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 06 December 2024, pp. 415-437
- Print publication:
- November 2024
-
- Article
- Export citation
DECOMPOSITION OF THE JACOBIAN OF SOME TWISTS OF A GENUS
 $2$ CURVE
$2$ CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 445-459
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1891-1916
- Print publication:
- December 2024
-
- Article
- Export citation
THE MORDELL–LANG CONJECTURE FOR SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 254-264
- Print publication:
- April 2024
-
- Article
- Export citation
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 91-127
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zariski dense orbits for regular self-maps of split semiabelian varieties in positive characteristic
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 479-519
- Print publication:
- November 2023
-
- Article
- Export citation
Elements of prime order in Tate–Shafarevich groups of abelian varieties over
 ${\mathbb Q}$
${\mathbb Q}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 November 2022, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the distribution of rational points on ramified covers of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 07 December 2022, pp. 2109-2155
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation