Refine search
Actions for selected content:
20 results
Local monodromy of Drinfeld modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2656-2683
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zagier–Hoffman’s Conjectures in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 October 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the integral part of A-motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1715-1783
- Print publication:
- August 2024
-
- Article
- Export citation
Algebraic relations among Goss’s zeta values on elliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 50-68
- Print publication:
- August 2023
-
- Article
- Export citation
Effective rigid analytic trivializations for Drinfeld modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 April 2022, pp. 713-742
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GENERIC FIBRE OF MODULI SPACES OF BOUNDED LOCAL G-SHTUKAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 799-878
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local Shtukas and Divisible Local Anderson Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1163-1207
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
The Distribution of the First Elementary Divisor of the Reductions of a Generic Drinfeld Module of Arbitrary Rank
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1326-1357
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Cyclic homology, Serre's local factors and λ-operations
-
- Journal:
- Journal of K-Theory / Volume 14 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 1-45
- Print publication:
- August 2014
-
- Article
- Export citation
Comptage des
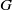 $G$-chtoucas: la partie elliptique
$G$-chtoucas: la partie elliptique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 2169-2183
- Print publication:
- December 2013
-
- Article
- Export citation
A NOTE ON THE GENUS OF GLOBAL FUNCTION FIELDS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 559-565
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
The André–Oort conjecture for Drinfeld modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 507-567
- Print publication:
- April 2013
-
- Article
- Export citation
Towards the Full Mordell–Lang Conjecture for Drinfeld Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 1 / 01 March 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-101
- Print publication:
- 01 March 2010
-
- Article
-
- You have access
- Export citation
Frobenius fields for Drinfeld modules of rank 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 827-848
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Galois modules arising from Faltings's strict modules
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 14 July 2006, pp. 867-888
- Print publication:
- July 2006
-
- Article
-
- You have access
- Export citation
Characteristic p Galois Representations That Arise from Drinfeld Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-293
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
Elliptic Units and Class Fields of Global Function Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 4 / 01 December 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-394
- Print publication:
- 01 December 1997
-
- Article
-
- You have access
- Export citation
Torsion Points of Drinfeld Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 1 / 01 March 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
- Print publication:
- 01 March 1995
-
- Article
-
- You have access
- Export citation



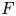
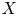
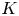
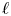
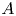

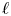
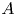
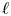
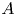
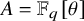
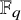
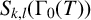
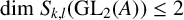
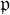
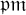
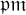
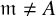
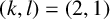
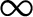
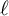
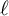
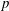
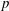


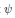
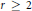
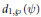
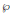
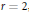
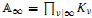 , provides the right theory to obtain, using λ-operations, Serre's archimedean local factors of the complex L-function of
, provides the right theory to obtain, using λ-operations, Serre's archimedean local factors of the complex L-function of 
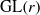
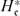
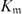
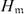
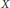
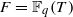 , with
, with 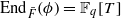 . Let
. Let 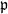 of good reduction for ϕ, let
of good reduction for ϕ, let 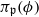 be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field
be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field 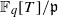 . Let Π
. Let Π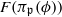 is the fixed imaginary quadratic field
is the fixed imaginary quadratic field 