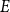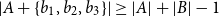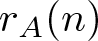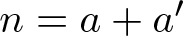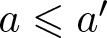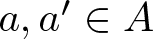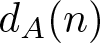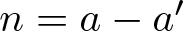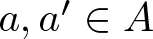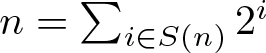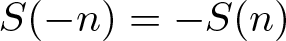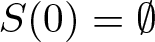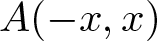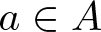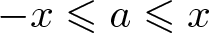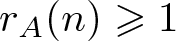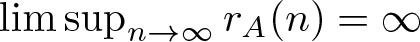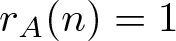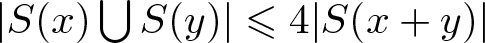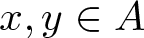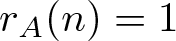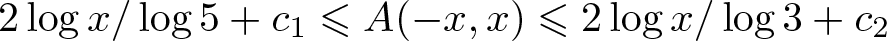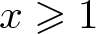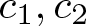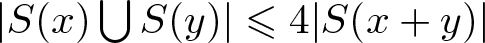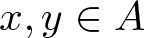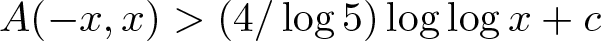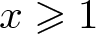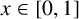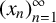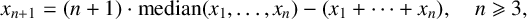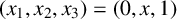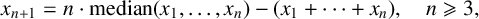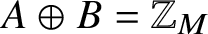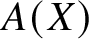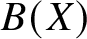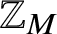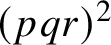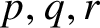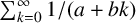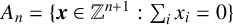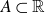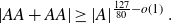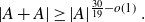Refine search
Actions for selected content:
38 results
ON ADDITIVE COMPLEMENTS IN THE COMPLEMENT OF A SET OF NATURAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-13
-
- Article
- Export citation
 $B_h$-sets of real and complex numbers
$B_h$-sets of real and complex numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-5
-
- Article
- Export citation
MONOTONIC COLLATZ SUBSEQUENCES WITH TERMS CONGRUENT MODULO A FIXED POWER OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 418-429
- Print publication:
- December 2025
-
- Article
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
The sum-product problem for integers with few prime factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 427-446
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An efficient asymmetric removal lemma and its limitations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product of polynomial values being large power
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 November 2024, pp. 51-62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 411-431
-
- Article
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
On the density of bounded bases
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 07 August 2023, pp. 832-844
-
- Article
- Export citation
THE AKIYAMA MEAN-MEDIAN MAP HAS UNBOUNDED TRANSIT TIME AND DISCONTINUOUS LIMIT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 298-307
- Print publication:
- October 2023
-
- Article
- Export citation
Combinatorial and harmonic-analytic methods for integer tilings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 March 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A GENERALISATION OF A THEOREM OF ERDŐS AND NIVEN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 215-223
- Print publication:
- October 2022
-
- Article
- Export citation
ABELIAN DIFFERENCE SETS AS LATTICE COVERINGS AND LATTICE TILINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 177-184
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
An update on the sum-product problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 411-430
- Print publication:
- September 2022
-
- Article
- Export citation
Solving equations in dense Sidon sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 19 May 2021, pp. 25-34
- Print publication:
- July 2022
-
- Article
- Export citation
ASKING QUESTIONS TO DETERMINE THE PRODUCT OF CIRCULARLY ARRANGED NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 April 2021, pp. 187-195
- Print publication:
- October 2021
-
- Article
- Export citation
ON ASYMPTOTIC BASES WHICH HAVE DISTINCT SUBSET SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 211-217
- Print publication:
- October 2021
-
- Article
- Export citation