Introduction. In his monograph On Numbers and Games [7], J. H. Conway introduced a real-closed field containing the reals and the ordinals as well as a great many other numbers including ω, ω, /2, 1/ω, 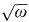 and ω − π to name only a few. Indeed, this particular real-closed field, which Conway calls No, is so remarkably inclusive that, subject to the proviso that numbers—construed here as members of ordered “number” fields—be individually definable in terms of sets of von Neumann-Bernays-Gödel set theory with Global Choice, henceforth NBG [cf. 21, Ch. 4], it may be said to contain “All Numbers Great and Small.” In this respect, No bears much the same relation to ordered fields that the system of real numbers bears to Archimedean ordered fields. This can be made precise by saying that whereas the ordered field of reals is (up to isomorphism) the unique homogeneous universal Archimedean ordered field, No is (up to isomorphism) the unique homogeneous universal orderedfield [14]; also see [10], [12], [13].
and ω − π to name only a few. Indeed, this particular real-closed field, which Conway calls No, is so remarkably inclusive that, subject to the proviso that numbers—construed here as members of ordered “number” fields—be individually definable in terms of sets of von Neumann-Bernays-Gödel set theory with Global Choice, henceforth NBG [cf. 21, Ch. 4], it may be said to contain “All Numbers Great and Small.” In this respect, No bears much the same relation to ordered fields that the system of real numbers bears to Archimedean ordered fields. This can be made precise by saying that whereas the ordered field of reals is (up to isomorphism) the unique homogeneous universal Archimedean ordered field, No is (up to isomorphism) the unique homogeneous universal orderedfield [14]; also see [10], [12], [13].
However, in addition to its distinguished structure as an ordered field, No has a rich hierarchical structure that (implicitly) emerges from the recursive clauses in terms of which it is defined. This algebraico-tree-theoretic structure, or simplicity hierarchy, as we have called it [15], depends upon No's (implicit) structure as a lexicographically ordered binary tree and arises from the fact that the sums and products of any two members of the tree are the simplest possible elements of the tree consistent with No's structure as an ordered group and an ordered field, respectively, it being understood that x is simpler than y just in case x is a predecessor of y in the tree.