Article contents
Cohen-stable families of subsets of integers
Published online by Cambridge University Press: 12 March 2014
Abstract
A maximal almost disjoint (mad) family 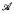 ⊆ [ω]ω is Cohen-stable if and only if it remains maximal in any Cohen generic extension. Otherwise it is Cohen-unstable. It is shown that a mad family.
⊆ [ω]ω is Cohen-stable if and only if it remains maximal in any Cohen generic extension. Otherwise it is Cohen-unstable. It is shown that a mad family. 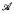 .is Cohen-unstable if and only if there is a bijection G from ω to the rationals such that the sets G[A]. A ∈
.is Cohen-unstable if and only if there is a bijection G from ω to the rationals such that the sets G[A]. A ∈ 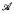 are nowhere dense. An ℵ0-mad family,
are nowhere dense. An ℵ0-mad family, 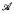 . is a mad family with the property that given any countable family ℬ ⊂ [ω]ω such that each element of ℬ meets infinitely many elements of
. is a mad family with the property that given any countable family ℬ ⊂ [ω]ω such that each element of ℬ meets infinitely many elements of 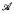 in an infinite set there is an element of
in an infinite set there is an element of 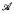 meeting each element of ℬ in an infinite set. It is shown that Cohen-stable mad families exist if and only if there exist ℵ0-mad families. Either of the conditions b = c or a < cov(
meeting each element of ℬ in an infinite set. It is shown that Cohen-stable mad families exist if and only if there exist ℵ0-mad families. Either of the conditions b = c or a < cov(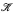 ) implies that there exist Cohen-stable mad families. Similar results are obtained for splitting families. For example, a splitting family.
) implies that there exist Cohen-stable mad families. Similar results are obtained for splitting families. For example, a splitting family. 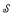 . is Cohen-unstable if and only if there is a bijection G from ω to the rationals such that the boundaries of the sets G[S], S ∈
. is Cohen-unstable if and only if there is a bijection G from ω to the rationals such that the boundaries of the sets G[S], S ∈ 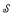 are nowhere dense. Also. Cohen-stable splitting families of cardinality ≤ κ exist if and only if ℵ0-splitting families of cardinality ≤ κ exist.
are nowhere dense. Also. Cohen-stable splitting families of cardinality ≤ κ exist if and only if ℵ0-splitting families of cardinality ≤ κ exist.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 17
- Cited by

