Article contents
Initial segments of the lattice of Π10 classes
Published online by Cambridge University Press: 12 March 2014
Abstract.
We show that in the lattice 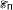 of
of 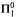 classes there are initial segments [∅, P] =
classes there are initial segments [∅, P] = 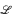 (P) which are not Boolean algebras, but which have a decidable theory. In fact, we will construct for any finite distributive lattice L which satisfies the dual of the usual reduction property a
(P) which are not Boolean algebras, but which have a decidable theory. In fact, we will construct for any finite distributive lattice L which satisfies the dual of the usual reduction property a 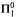 class P such that L is isomorphic to the lattice
class P such that L is isomorphic to the lattice 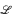 (P)*, which is
(P)*, which is 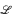 (P). modulo finite differences. For the 2-element lattice, we obtain a minimal class, first constructed by Cenzer, Downey, Jockusch and Shore in 1993. For the simplest new
(P). modulo finite differences. For the 2-element lattice, we obtain a minimal class, first constructed by Cenzer, Downey, Jockusch and Shore in 1993. For the simplest new 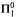 class P constructed, P has a single, non-computable limit point and
class P constructed, P has a single, non-computable limit point and 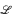 (P)* has three elements, corresponding to ∅, P and a minimal class P0 ⊂ P, The element corresponding to P0 has no complement in the lattice. On the other hand, the theory of
(P)* has three elements, corresponding to ∅, P and a minimal class P0 ⊂ P, The element corresponding to P0 has no complement in the lattice. On the other hand, the theory of 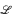 (P) is shown to be decidable.
(P) is shown to be decidable.
A 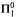 class P is said to be decidable if it is the set of paths through a computable tree with no dead ends. We show that if P is decidable and has only finitely many limit points, then
class P is said to be decidable if it is the set of paths through a computable tree with no dead ends. We show that if P is decidable and has only finitely many limit points, then 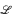 (P)* is always a Boolean algebra. We show that if P is a decidable
(P)* is always a Boolean algebra. We show that if P is a decidable 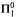 class and
class and 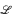 (P) is not a Boolean algebra, then the theory of
(P) is not a Boolean algebra, then the theory of 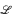 (P) interprets the theory of arithmetic and is therefore undecidable.
(P) interprets the theory of arithmetic and is therefore undecidable.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 3
- Cited by

