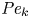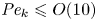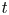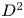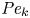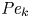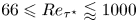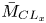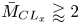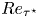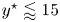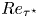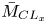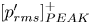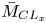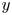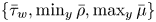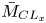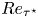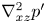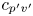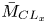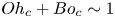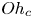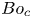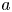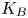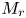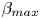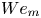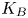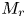doi:10.1017/jfm.2023.88 Alventosa et al. Inertio-capillary rebound of a droplet impacting a fluid bath
Contents
JFM Papers
The nonlinear Benjamin–Feir instability – Hamiltonian dynamics, discrete breathers and steady solutions
-
- Published online by Cambridge University Press:
- 01 March 2023, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Droplet evaporation in inert gases
-
- Published online by Cambridge University Press:
- 01 March 2023, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling of pressure fluctuations in compressible turbulent plane channel flow
-
- Published online by Cambridge University Press:
- 03 March 2023, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
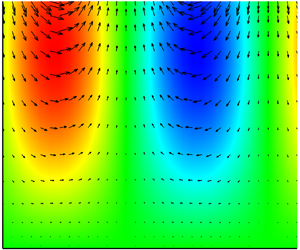
Rotational dynamics of a neutrally buoyant prolate spheroid in viscoelastic shear flows at finite Reynolds numbers
-
- Published online by Cambridge University Press:
- 03 March 2023, A20
-
- Article
- Export citation
Inertia-gravity-wave diffusion by geostrophic turbulence: the impact of flow time dependence
-
- Published online by Cambridge University Press:
- 03 March 2023, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surface wave instability in the thermocapillary migration of a flat droplet
-
- Published online by Cambridge University Press:
- 03 March 2023, A22
-
- Article
- Export citation
A second-order constitutive theory for polyatomic gases: theory and applications
-
- Published online by Cambridge University Press:
- 03 March 2023, A23
-
- Article
- Export citation
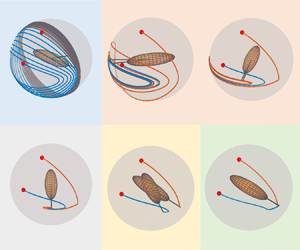
Inertio-capillary rebound of a droplet impacting a fluid bath
-
- Published online by Cambridge University Press:
- 03 March 2023, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drop impact on viscous liquid films
-
- Published online by Cambridge University Press:
- 06 March 2023, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
When does an impacting drop stop bouncing?
-
- Published online by Cambridge University Press:
- 06 March 2023, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental characterisation and data-driven modelling of unsteady wall pressure fields induced by a supersonic jet over a tangential flat plate
-
- Published online by Cambridge University Press:
- 06 March 2023, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rossby waves past the breaking point in zonally dominated turbulence
-
- Published online by Cambridge University Press:
- 06 March 2023, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential asymptotics and the generation of free-surface flows by submerged line vortices
-
- Published online by Cambridge University Press:
- 06 March 2023, A29
-
- Article
- Export citation
The Lyman–Huggins interpretation of enstrophy transport
-
- Published online by Cambridge University Press:
- 06 March 2023, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entrainment mechanism of turbulent synthetic jet flow
-
- Published online by Cambridge University Press:
- 06 March 2023, A31
-
- Article
- Export citation
Ion emission from nanodroplets undergoing Coulomb explosions: a continuum numerical study
-
- Published online by Cambridge University Press:
- 07 March 2023, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experiments on Marangoni spreading – evidence of a new type of interfacial instability
-
- Published online by Cambridge University Press:
- 07 March 2023, A33
-
- Article
- Export citation
Viscoplastic lines: printing a single filament of yield stress material on a surface
-
- Published online by Cambridge University Press:
- 07 March 2023, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling maximum spreading of droplet impacting on flexible substrates
-
- Published online by Cambridge University Press:
- 07 March 2023, A35
-
- Article
- Export citation
On the nonlinear behaviour of the Rayleigh–Taylor instability with a tangential electric field for inviscid and perfect dielectric fluids
-
- Published online by Cambridge University Press:
- 09 March 2023, A36
-
- Article
- Export citation