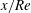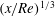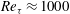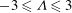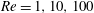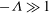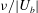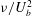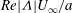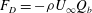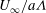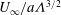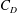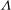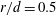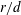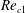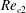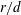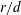Contents
Papers
Prediction of noise from serrated trailing edges
-
- Published online by Cambridge University Press:
- 18 March 2016, pp. 556-588
-
- Article
- Export citation
Subcritical instability of finite circular Couette flow with stationary inner cylinder
-
- Published online by Cambridge University Press:
- 18 March 2016, pp. 589-611
-
- Article
- Export citation
Vortex interaction between two tandem flexible propulsors with a paddling-based locomotion
-
- Published online by Cambridge University Press:
- 18 March 2016, pp. 612-632
-
- Article
- Export citation
Influence of flow topology and dilatation on scalar mixing in compressible turbulence
-
- Published online by Cambridge University Press:
- 18 March 2016, pp. 633-655
-
- Article
- Export citation
Fishlike rheotaxis
-
- Published online by Cambridge University Press:
- 18 March 2016, pp. 656-666
-
- Article
- Export citation
Slipping free jet flow near channel exit at moderate Reynolds number for large slip length
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 667-708
-
- Article
- Export citation
Computations of equilibrium and non-equilibrium turbulent channel flows using a nested-LES approach
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 709-748
-
- Article
- Export citation
Vortex breakdown in premixed reacting flows with swirl in a finite-length circular open pipe
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 749-776
-
- Article
- Export citation
Self-consistent model for the saturation mechanism of the response to harmonic forcing in the backward-facing step flow
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 777-797
-
- Article
- Export citation
The effect of a uniform through-surface flowon a cylinder and sphere
-
- Published online by Cambridge University Press:
- 23 March 2016, pp. 798-839
-
- Article
- Export citation
Evolution of material surfaces in the temporal transition in channel flow
-
- Published online by Cambridge University Press:
- 23 March 2016, pp. 840-876
-
- Article
- Export citation
Solute dispersion in pulsatile Casson fluid flow in a tube with wall absorption
-
- Published online by Cambridge University Press:
- 23 March 2016, pp. 877-914
-
- Article
- Export citation
Flow instabilities in the wake of a rounded square cylinder
-
- Published online by Cambridge University Press:
- 23 March 2016, pp. 915-932
-
- Article
- Export citation
Stratified tidal flow over a tall ridge above and below the turning latitude
-
- Published online by Cambridge University Press:
- 29 March 2016, pp. 933-957
-
- Article
- Export citation
Rapids
On turbulent particle fountains
-
- Published online by Cambridge University Press:
- 23 March 2016, R1
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 793 Cover and Front matter
-
- Published online by Cambridge University Press:
- 11 April 2016, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
FLM volume 793 Cover and Back matter
-
- Published online by Cambridge University Press:
- 11 April 2016, pp. b1-b3
-
- Article
-
- You have access
- Export citation