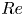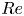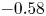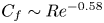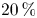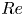doi:10.1017/jfm.2024.1105 Dandekar et al. Splash on a liquid pool: coupled cavity-sheet unsteady dynamics
Contents
JFM Papers
Instability of a dusty shear flow
-
- Published online by Cambridge University Press:
- 27 December 2024, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intrinsic phase-based proper orthogonal decomposition (IPhaB POD): a method for physically interpretable modes in near-periodic systems
-
- Published online by Cambridge University Press:
- 09 January 2025, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A statistically stationary minimal flow unit for self-similar Rayleigh–Taylor turbulence in the mode-coupling limit
-
- Published online by Cambridge University Press:
- 09 January 2025, A19
-
- Article
- Export citation
Linear analysis characterizes pressure gradient history effects in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 03 January 2025, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Accurate models of the added mass force of a uniform random distribution of spherical particles or bubbles
-
- Published online by Cambridge University Press:
- 09 January 2025, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regimes of near-inertial wave dynamics
-
- Published online by Cambridge University Press:
- 09 January 2025, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of solitary waves on a ferrofluid jet: the Hamiltonian framework
-
- Published online by Cambridge University Press:
- 09 January 2025, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Hamiltonian Dysthe equation for hydroelastic waves in a compressed ice sheet
-
- Published online by Cambridge University Press:
- 06 January 2025, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of mushy layers grown from perfectly and imperfectly conducting boundaries. Part 1. Diffusive solidification
-
- Published online by Cambridge University Press:
- 03 January 2025, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of mushy layers grown from perfectly and imperfectly conducting boundaries. Part 2. Onset of convection
-
- Published online by Cambridge University Press:
- 03 January 2025, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formation of super-stable granular heaps
-
- Published online by Cambridge University Press:
- 03 January 2025, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted finite wing at low Reynolds number: cellular vortex shedding, wing-tip vortex and aerodynamic performance
-
- Published online by Cambridge University Press:
- 03 January 2025, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moment of momentum integral analysis of turbulent boundary layers with pressure gradient
-
- Published online by Cambridge University Press:
- 03 January 2025, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear coherent structures in 2-D plane Couette flow with constant throughflow
-
- Published online by Cambridge University Press:
- 03 January 2025, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An intermittency based Reynolds-averaged transition model for mixing flows induced by interfacial instabilities
-
- Published online by Cambridge University Press:
- 03 January 2025, A31
-
- Article
- Export citation
Inverse Leidenfrost impacting drops
-
- Published online by Cambridge University Press:
- 03 January 2025, A32
-
- Article
- Export citation
Global drag reduction and local flow statistics in Taylor–Couette turbulence with dilute polymer additives
-
- Published online by Cambridge University Press:
- 03 January 2025, A33
-
- Article
- Export citation
Instability of falling films of discontinuously shear-thickening fluid
-
- Published online by Cambridge University Press:
- 03 January 2025, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interpretation of the amplitude modulation coefficient and a new transport-based coefficient
-
- Published online by Cambridge University Press:
- 03 January 2025, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Active volume of water in a laboratory aquifer
-
- Published online by Cambridge University Press:
- 27 January 2025, A36
-
- Article
- Export citation