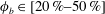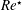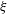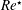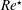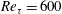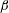Contents
JFM Papers
Shape and rheology of droplets with viscous surface moduli
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 385-420
-
- Article
- Export citation
Nozzle external geometry as a boundary condition for the azimuthal mode selection in an impinging underexpanded jet
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 421-448
-
- Article
- Export citation
A Lagrangian probability-density-function model for collisional turbulent fluid–particle flows
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 449-489
-
- Article
- Export citation
Incipient bedforms in a bidirectional wind regime
-
- Published online by Cambridge University Press:
- 14 January 2019, pp. 490-516
-
- Article
- Export citation
Analytical solutions for mass transport in hydrodynamic focusing by considering different diffusivities for sample and sheath flows
-
- Published online by Cambridge University Press:
- 14 January 2019, pp. 517-551
-
- Article
- Export citation
A new model of shoaling and breaking waves: one-dimensional solitary wave on a mild sloping beach
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 552-591
-
- Article
- Export citation
Collision and breakup of fractal particle agglomerates in a shear flow
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 592-623
-
- Article
- Export citation
A numerical study on reaction-induced radial fingering instability
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 624-638
-
- Article
- Export citation
Stratified shear instability in a field of pre-existing turbulence
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 639-658
-
- Article
- Export citation
Fully developed and transient concentration profiles of particulate suspensions sheared in a cylindrical Couette cell
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 659-671
-
- Article
- Export citation
Thermohaline layering on the microscale
-
- Published online by Cambridge University Press:
- 14 January 2019, pp. 672-695
-
- Article
- Export citation
The electrostatically forced Faraday instability: theory and experiments
-
- Published online by Cambridge University Press:
- 14 January 2019, pp. 696-731
-
- Article
- Export citation
Elastohydrodynamics of a pre-stretched finite elastic sheet lubricated by a thin viscous film with application to microfluidic soft actuators
-
- Published online by Cambridge University Press:
- 14 January 2019, pp. 732-752
-
- Article
- Export citation
Rough or wiggly? Membrane topology and morphology for fouling control
-
- Published online by Cambridge University Press:
- 14 January 2019, pp. 753-780
-
- Article
- Export citation
Direct numerical simulation of turbulence over systematically varied irregular rough surfaces
-
- Published online by Cambridge University Press:
- 25 January 2019, pp. 781-815
-
- Article
- Export citation
Absolute and convective instabilities in electrohydrodynamic flow subjected to a Poiseuille flow: a linear analysis
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 816-844
-
- Article
- Export citation
The instantaneous structure of secondary flows in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 845-870
-
- Article
- Export citation
Thrust, drag and wake structure in flapping compliant membrane wings
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 871-888
-
- Article
- Export citation
Is spontaneous generation of coherent baroclinic flows possible?
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 889-923
-
- Article
- Export citation
Water entry of an expanding body with and without splash
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 924-950
-
- Article
- Export citation