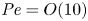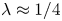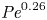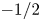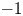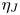Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
Intrinsic compressibility effects in near-wall turbulence
-
- Published online by Cambridge University Press:
- 07 March 2025, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Elements of Gasdynamics, by H. W. LIEPMANN and A. ROSHKO. New York: John Wiley & Sons, 1957. 439 pp. $11.00 or 88s.
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 658-661
-
- Article
- Export citation
- Cited by 1
Lateral migration and bouncing of a deformable bubble rising near a vertical wall. Part 2. Highly inertial regimes
-
- Published online by Cambridge University Press:
- 18 June 2025, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Upper bound of heat flux in an anelastic model for Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 21 November 2024, A94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Acoustothermal effect: mechanism and quantification of the heat source
-
- Published online by Cambridge University Press:
- 04 June 2025, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Scalar transport across the interface between a random sphere pack and a turbulent flow
-
- Published online by Cambridge University Press:
- 28 May 2025, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
On elementary four-wave interactions in dispersive media
-
- Published online by Cambridge University Press:
- 19 March 2024, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Surface tension force on a partially submerged horizontal concave cylinder
-
- Published online by Cambridge University Press:
- 18 October 2022, A15
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
Mass transfer from small spheroids suspended in a turbulent fluid
-
- Published online by Cambridge University Press:
- 21 October 2021, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Viscous gravity currents over flat inclined surfaces
-
- Published online by Cambridge University Press:
- 23 November 2021, A12
-
- Article
- Export citation
- Cited by 1
Estimating forces during ploughing of a granular bed
-
- Published online by Cambridge University Press:
- 19 July 2019, pp. 376-410
-
- Article
- Export citation
- Cited by 1
Assessment of local isotropy, energetics, and modified eddy-viscosity based modelling for particle-laden turbulent channel flows
-
- Published online by Cambridge University Press:
- 04 September 2023, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Resonances and instabilities in a tilted rotating annulus
-
- Published online by Cambridge University Press:
- 20 October 2023, A34
-
- Article
- Export citation
- Cited by 1
Periodic flow features in a planar sudden expansion with pulsatile inflow velocity
-
- Published online by Cambridge University Press:
- 06 February 2024, A43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Hydrodynamics of rowing propulsion
-
- Published online by Cambridge University Press:
- 11 May 2021, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
The drainage of glacier and ice sheet surface lakes
-
- Published online by Cambridge University Press:
- 14 April 2023, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Resonant triad interactions of two acoustic modes and a gravity wave
-
- Published online by Cambridge University Press:
- 07 April 2025, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Oblique instability of a stratified oscillatory boundary layer
-
- Published online by Cambridge University Press:
- 23 December 2021, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
PROFESSOR CHARLES ROGERS DOERING 7 January 1956–15 May 2021
-
- Published online by Cambridge University Press:
- 21 July 2021, E1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
Phase dynamics of freely swimming foils
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 5-21
-
- Article
- Export citation