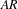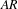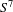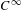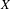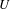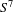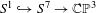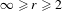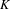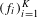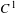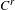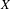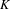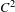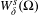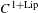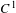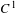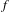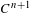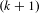Contents
Original Article
Lower bounds for the decay of correlations in non-uniformly expanding maps
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 1936-1970
-
- Article
- Export citation
Corrigendum
The Toeplitz noncommutative solenoid and its Kubo–Martin–Schwinger states – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 17 December 2018, p. 2592
-
- Article
-
- You have access
- Export citation
Original Article
Homotopical complexity of a billiard flow on the 3D flat torus with two cylindrical obstacles
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 1071-1081
-
- Article
- Export citation
Statistics of patterns in typical cut and project sets
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3365-3387
-
- Article
- Export citation
Some properties of distal actions on locally compact groups
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 1340-1360
-
- Article
- Export citation
Polynomial decay of correlations for almost Anosov diffeomorphisms
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 832-864
-
- Article
- Export citation
Smooth foliations by circles of
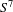 $S^{7}$ with unbounded periods and nonlinearizable multicentres
$S^{7}$ with unbounded periods and nonlinearizable multicentres
-
- Published online by Cambridge University Press:
- 04 May 2017, pp. 257-288
-
- Article
- Export citation
On stable transitivity of finitely generated groups of volume-preserving diffeomorphisms
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 554-576
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 39 Issue 10 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 September 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Original Article
Dynamical simplices and Fraïssé theory
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3111-3126
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 39 Issue 8 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 39 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Original Article
On the arithmetic dynamics of monomial maps
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3388-3406
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 39 Issue 9 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 August 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ETS volume 39 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Original Article
Shy shadows of infinite-dimensional partially hyperbolic invariant sets
-
- Published online by Cambridge University Press:
- 25 September 2017, pp. 1361-1400
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 39 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 28 November 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Original Article
Birkhoff sum fluctuations in substitution dynamical systems
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 1971-2005
-
- Article
- Export citation
No round wandering domains for
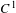 $C^{1}$-diffeomorphisms of tori
$C^{1}$-diffeomorphisms of tori
-
- Published online by Cambridge University Press:
- 10 April 2018, pp. 3127-3135
-
- Article
- Export citation
Singular analytic linear cocycles with negative infinite Lyapunov exponents
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 1082-1098
-
- Article
- Export citation