Article contents
Smooth foliations by circles of 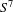 $S^{7}$ with unbounded periods and nonlinearizable multicentres
$S^{7}$ with unbounded periods and nonlinearizable multicentres
Published online by Cambridge University Press: 04 May 2017
Abstract
We give an example of a 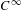 $C^{\infty }$ vector field
$C^{\infty }$ vector field  $X$, defined in a neighbourhood
$X$, defined in a neighbourhood 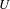 $U$ of
$U$ of 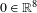 $0\in \mathbb{R}^{8}$, such that
$0\in \mathbb{R}^{8}$, such that 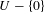 $U-\{0\}$ is foliated by closed integral curves of
$U-\{0\}$ is foliated by closed integral curves of 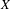 $X$, the differential
$X$, the differential 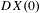 $DX(0)$ at
$DX(0)$ at  $0$ defines a one-parameter group of non-degenerate rotations and
$0$ defines a one-parameter group of non-degenerate rotations and 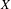 $X$ is not orbitally equivalent to its linearization. Such a vector field
$X$ is not orbitally equivalent to its linearization. Such a vector field 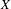 $X$ has the first integral
$X$ has the first integral  $I(x)=\Vert x\Vert ^{2}$, and its main feature is that its period function is locally unbounded near the stationary point. This proves in the
$I(x)=\Vert x\Vert ^{2}$, and its main feature is that its period function is locally unbounded near the stationary point. This proves in the 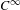 $C^{\infty }$ category that the classical Poincaré centre theorem, true for planar non-degenerate centres, is not generalizable to multicentres. Such an example is obtained through a careful study and a suitable modification of a celebrated example by Sullivan [A counterexample to the periodic orbit conjecture. Publ. Math. Inst. Hautes Études Sci. 46 (1976), 5–14], by blowing up the stationary point at the origin and through the construction of a smooth one-parameter family of foliations by circles of
$C^{\infty }$ category that the classical Poincaré centre theorem, true for planar non-degenerate centres, is not generalizable to multicentres. Such an example is obtained through a careful study and a suitable modification of a celebrated example by Sullivan [A counterexample to the periodic orbit conjecture. Publ. Math. Inst. Hautes Études Sci. 46 (1976), 5–14], by blowing up the stationary point at the origin and through the construction of a smooth one-parameter family of foliations by circles of 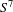 $S^{7}$ whose orbits have unbounded lengths (equivalently, unbounded periods) for each value of the parameter and which smoothly converges to the Hopf fibration
$S^{7}$ whose orbits have unbounded lengths (equivalently, unbounded periods) for each value of the parameter and which smoothly converges to the Hopf fibration 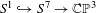 $S^{1}{\hookrightarrow}S^{7}\rightarrow \mathbb{CP}^{3}$.
$S^{1}{\hookrightarrow}S^{7}\rightarrow \mathbb{CP}^{3}$.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 1
- Cited by

