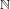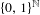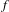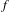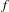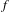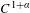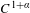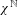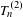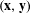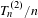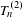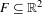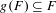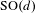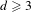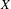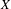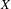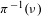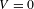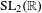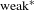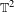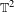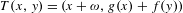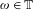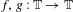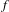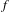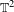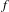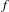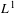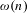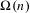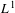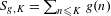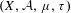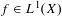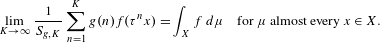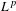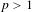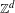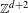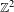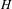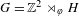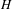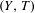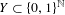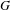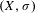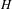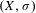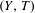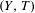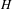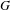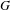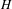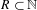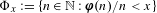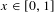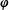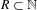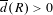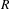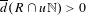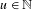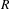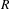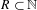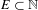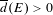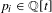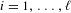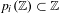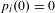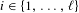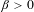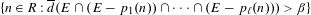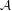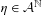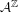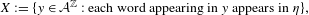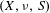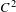Contents
Original Article
Approximate transitivity of the ergodic action of the group of finite permutations of
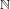 $\mathbb{N}$ on
$\mathbb{N}$ on  $\{0,1\}^{\mathbb{N}}$
$\{0,1\}^{\mathbb{N}}$
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 2881-2895
-
- Article
- Export citation
Non-rigidity for circle homeomorphisms with several break points
-
- Published online by Cambridge University Press:
- 28 November 2017, pp. 2305-2331
-
- Article
- Export citation
Lower bounds for the Ruelle spectrum of analytic expanding circle maps
-
- Published online by Cambridge University Press:
- 04 May 2017, pp. 289-310
-
- Article
- Export citation
Survey Article
Ergodic optimization in dynamical systems
-
- Published online by Cambridge University Press:
- 24 January 2018, pp. 2593-2618
-
- Article
-
- You have access
- Open access
- Export citation
Original Article
Ergodic boundary representations
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 2017-2047
-
- Article
- Export citation
On the statistical stability of Lorenz attractors with a
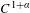 $C^{1+\unicode[STIX]{x1D6FC}}$ stable foliation
$C^{1+\unicode[STIX]{x1D6FC}}$ stable foliation
-
- Published online by Cambridge University Press:
- 16 April 2018, pp. 3169-3184
-
- Article
- Export citation
From the divergence between two measures to the shortest path between two observables
-
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1729-1744
-
- Article
- Export citation
Self-embeddings of Bedford–McMullen carpets
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 577-603
-
- Article
- Export citation
Survey Article
Notes on the multiplicative ergodic theorem
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 1153-1189
-
- Article
- Export citation
Original Article
Inhomogeneous self-similar sets with overlaps
-
- Published online by Cambridge University Press:
- 04 May 2017, pp. 1-18
-
- Article
- Export citation
Relative equilibrium states and class degree
-
- Published online by Cambridge University Press:
- 22 June 2017, pp. 865-888
-
- Article
- Export citation
Horocycle flow orbits and lattice surface characterizations
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 1441-1461
-
- Article
- Export citation
The set of uniquely ergodic interval exchange transformations is path-connected
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 311-356
-
- Article
- Export citation
Equilibrium stability for non-uniformly hyperbolic systems
-
- Published online by Cambridge University Press:
- 18 January 2018, pp. 2619-2642
-
- Article
- Export citation
On some generalizations of skew-shifts on
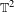 $\mathbb{T}^{2}$
$\mathbb{T}^{2}$
-
- Published online by Cambridge University Press:
- 04 May 2017, pp. 19-61
-
- Article
- Export citation
Ergodic averages with prime divisor weights in
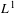 $L^{1}$
$L^{1}$
-
- Published online by Cambridge University Press:
- 18 August 2017, pp. 889-897
-
- Article
- Export citation
A generalization of the simulation theorem for semidirect products
-
- Published online by Cambridge University Press:
- 10 April 2018, pp. 3185-3206
-
- Article
- Export citation
Rationally almost periodic sequences, polynomial multiple recurrence and symbolic dynamics
-
- Published online by Cambridge University Press:
- 18 January 2018, pp. 2332-2383
-
- Article
- Export citation
Ergodic properties of bimodal circle maps
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 1462-1500
-
- Article
- Export citation
Continuum-wise expansivity and entropyfor flows
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 1190-1210
-
- Article
- Export citation