Contents
Research Article
On a Question of Colin Clark Concerning Three Properties of Convex Sets(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 535-537
-
- Article
-
- You have access
- Export citation
Decomposition of the Multivariate Beta Distribution with Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-228
-
- Article
-
- You have access
- Export citation
Une Caracterisation de la Categorie des Groupes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 375-380
-
- Article
-
- You have access
- Export citation
Bounds for Characteristic Values of Positive Definite Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 51-56
-
- Article
-
- You have access
- Export citation
Existence Theorem for the Initial-Boundary Value Problem for a Singular Parabolic Partial Differential Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 229-234
-
- Article
-
- You have access
- Export citation
On the Finite Two-Dimensional Linear Groups II.(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 539-546
-
- Article
-
- You have access
- Export citation
Variations on the Hamiltonian Theme
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 57-62
-
- Article
-
- You have access
- Export citation
A Note on an Iterative Test of Edelstein(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-386
-
- Article
-
- You have access
- Export citation
On Unbiased Estimation of a Vector Parameter
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-550
-
- Article
-
- You have access
- Export citation
Noetherian Tensor Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 235-238
-
- Article
-
- You have access
- Export citation
Some Theorems on Strong Nörlund Summability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-69
-
- Article
-
- You have access
- Export citation
On a Class of Multivalued Mappings in Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 387-393
-
- Article
-
- You have access
- Export citation
Distribution of the Sum of Variates from Truncated Discrete Populations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 395-398
-
- Article
-
- You have access
- Export citation
Diagonals of Doubly Stochastic Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-241
-
- Article
-
- You have access
- Export citation
Approximation of Functions by a Bernstein-Type Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 551-557
-
- Article
-
- You have access
- Export citation
Riemannian Structures Subordinate to Certain Almost Tangent Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-77
-
- Article
-
- You have access
- Export citation
Mean Value Theorem for the m-Integral of Dinculeanu
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 243-251
-
- Article
-
- You have access
- Export citation
Local Malcev Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 559-568
-
- Article
-
- You have access
- Export citation
The Ring Scheme Fg
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-85
-
- Article
-
- You have access
- Export citation
Functions with a Finite Number of Negative Squares
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 399-410
-
- Article
-
- You have access
- Export citation
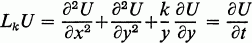
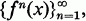 where
where 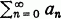 is a series, we shall use the notation
is a series, we shall use the notation 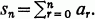 For a real, define
For a real, define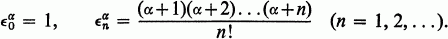
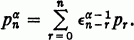
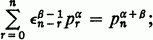
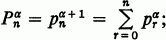
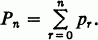
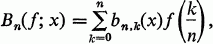
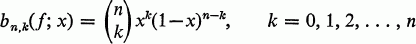
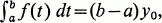 , where inf
, where inf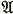 is an algebra, L(
is an algebra, L(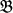 such that for each finite subset
such that for each finite subset 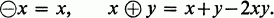
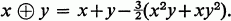
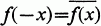 for every x∊
for every x∊