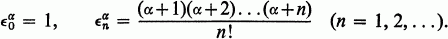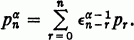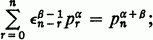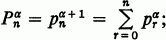Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boos, Johann
1978.
Konvexit�t der (C, ?)-Verfahren.
Archiv der Mathematik,
Vol. 31,
Issue. 1,
p.
151.
Taylor, Simon
1999.
The Harmonisation of European Product Liability Rules: French and English Law.
International and Comparative Law Quarterly,
Vol. 48,
Issue. 2,
p.
419.

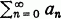 is a series, we shall use the notation
is a series, we shall use the notation 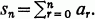 For a real, define
For a real, define