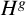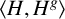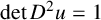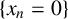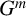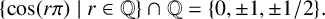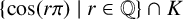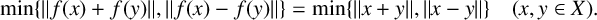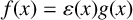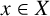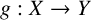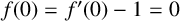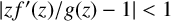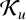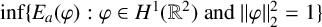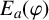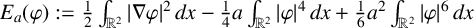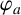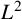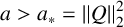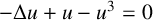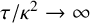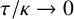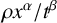Research Article
LOCALLY FINITE SIMPLE GROUPS WHOSE NONNILPOTENT SUBGROUPS ARE PRONORMAL
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2023, pp. 512-521
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JACOBIAN ELLIPTIC FUNCTIONS IN SIGNATURE FOUR
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2023, pp. 110-124
-
- Article
-
- You have access
- HTML
- Export citation
THE GROWTH OF SOLUTIONS OF MONGE–AMPÈRE EQUATIONS IN HALF SPACES AND ITS APPLICATION
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2023, pp. 125-137
-
- Article
-
- You have access
- HTML
- Export citation
FINITE GROUPS WITH HEREDITARILY G-PERMUTABLE SCHMIDT SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 July 2023, pp. 522-528
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE SOLVABLE TIDY GROUPS ARE DETERMINED BY HALL SUBGROUPS WITH TWO PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2023, pp. 342-349
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH FEW NONPOWER SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2023, pp. 529-540
-
- Article
-
- You have access
- HTML
- Export citation
FINITE BASIS PROBLEM FOR INVOLUTION MONOIDS OF ORDER FIVE
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2023, pp. 350-364
-
- Article
-
- You have access
- HTML
- Export citation
A DYNAMICAL SYSTEM PROOF OF NIVEN’S THEOREM AND ITS EXTENSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2023, pp. 138-151
-
- Article
-
- You have access
- HTML
- Export citation
MIN-PHASE-ISOMETRIES IN STRICTLY CONVEX NORMED SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2023, pp. 152-160
-
- Article
-
- You have access
- HTML
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2023, pp. 365-375
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON NORMALISED GROUND STATES FOR THE TWO-DIMENSIONAL CUBIC-QUINTIC NONLINEAR SCHRÖDINGER EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2023, pp. 552-561
-
- Article
-
- You have access
- HTML
- Export citation
REFLEXIVITY INDEX OF THE PRODUCT OF SOME TOPOLOGICAL SPACES AND LATTICES
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2023, pp. 376-387
-
- Article
-
- You have access
- HTML
- Export citation
PhD Abstract
CAYLEY GRAPHS AND GRAPHICAL REGULAR REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2023, pp. 161-162
-
- Article
-
- You have access
- HTML
- Export citation
HARMONIC-MEASURE DISTRIBUTION FUNCTIONS AND RELATED FUNCTIONS FOR SIMPLY CONNECTED AND MULTIPLY CONNECTED TWO-DIMENSIONAL REGIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2023, pp. 163-164
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
THE RESTRICTED CONNECTED HULL: FILLING THE HOLE
- Part of:
-
- Published online by Cambridge University Press:
- 20 April 2023, pp. 388-392
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON REAL NONISOMORPHIC BANACH SPACES WITH HOMEOMORPHIC GEOMETRIC STRUCTURE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2023, pp. 562-570
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PhD Abstract
EVENTUAL POSITIVITY AND ASYMPTOTIC BEHAVIOUR FOR HIGHER-ORDER EVOLUTION EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 26 October 2023, pp. 165-167
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
CONDITIONS FOR RECURRENCE AND TRANSIENCE FOR TIME-INHOMOGENEOUS BIRTH-AND-DEATH PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 23 June 2023, pp. 393-402
-
- Article
-
- You have access
- HTML
- Export citation