Refine listing
Actions for selected content:
264 results in 17Bxx
Verma modules over Virasoro-like algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-191
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Gradings of non-graded Hamiltonian Lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-440
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Finite-dimensional odd Hamiltonian superalgebras over a field of prime characteristic
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-130
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Ado-Iwasawa extras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 407-421
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Modular Lie representations of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-424
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Correspondences of the Gelfand invariants in reductive dual pairs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-278
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
The Wielandt Subalgebra of a Lie Algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-330
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
On
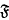 -hyperexcentric modules for Lie algebras
-hyperexcentric modules for Lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-238
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Multipartitions, generalized Durfee squares and affine Lie algebra characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 01 August 2017, pp. 395-408
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Lie powers of free modules for certain groups of prime power order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-158
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
A note on minimal coverings of groups by subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-168
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Restricted Lazard elimination and modular Lie powers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-278
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Equivalence of certain categories of modules for quantized affine lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-175
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
The orders of nonsingular derivations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 254-260
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Some thin Lie algebras related to Albert-Frank algebras and algebras of maximal class
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-184
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Free Lie algebras as modules for symmetric groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-156
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Distance to the convex hull of an orbit under the action of a compact Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-357
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
On the support of irreducible modules over the Witt–Kaplansky algebras of rank (2, 2)
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 381-389
- Print publication:
- December 1998
-
- Article
- Export citation
Finitely sorting Lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-363
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
Lie rings of groups of prime exponent
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-398
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
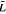 , indexed by
, indexed by  be a saturated formation of soluble Lie algebras and suppose that
be a saturated formation of soluble Lie algebras and suppose that 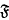 -hyperexcentric modules for Lie algebras
-hyperexcentric modules for Lie algebras
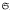 , of all permutations of a free generating set of
, of all permutations of a free generating set of 