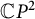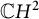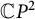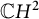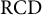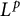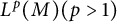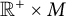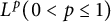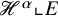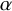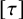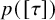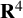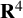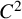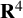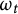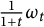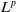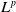Refine listing
Actions for selected content:
476 results in 53Cxx
Nonexistence of non-Hopf Ricci-semisymmetric real hypersurfaces in
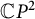 $\mathbb {C}P^{2}$ and
$\mathbb {C}P^{2}$ and 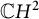 $\mathbb {C}H^{2}$
$\mathbb {C}H^{2}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 August 2023, pp. 188-200
- Print publication:
- March 2024
-
- Article
- Export citation
A note about charts built by Eriksson-Bique and Soultanis on metric measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 49-59
- Print publication:
- March 2024
-
- Article
- Export citation
Uniqueness of
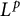 $L^p$ subsolutions to the heat equation on Finsler measure spaces
$L^p$ subsolutions to the heat equation on Finsler measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 166-175
- Print publication:
- March 2024
-
- Article
- Export citation
Foliated affine and projective structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1153-1187
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On sets with unit Hausdorff density in homogeneous groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 May 2023, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Total mean curvature surfaces in the product space
 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 346-365
-
- Article
- Export citation
Rigidity of capillary surfaces in compact 3-manifolds with strictly convex boundary
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 231-240
-
- Article
- Export citation
Biharmonic almost complex structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some characterizations of expanding and steady Ricci solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 446-449
- Print publication:
- May 2023
-
- Article
- Export citation
REILLY-TYPE UPPER BOUNDS FOR THE p-STEKLOV PROBLEM ON SUBMANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 492-503
- Print publication:
- December 2023
-
- Article
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation
Stable anisotropic minimal hypersurfaces in
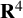 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of generalized Einstein metrics on three-dimensional Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 2038-2095
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Second-order estimates for collapsed limits of Ricci-flat Kähler metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 912-926
- Print publication:
- September 2023
-
- Article
- Export citation
On the pluriclosed flow on Oeljeklaus–Toma manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 39-65
- Print publication:
- February 2024
-
- Article
- Export citation
Geometric filling curves on punctured surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 383-400
- Print publication:
- May 2023
-
- Article
- Export citation
On intersection probabilities of four lines inside a planar convex domain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 December 2022, pp. 504-527
- Print publication:
- June 2023
-
- Article
- Export citation
AN OBSERVATION ON THE DIRICHLET PROBLEM AT INFINITY IN RIEMANNIAN CONES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 352-364
- Print publication:
- June 2023
-
- Article
- Export citation
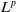 $L^p$ harmonic 1-forms on hypersurfaces with finite index
$L^p$ harmonic 1-forms on hypersurfaces with finite index
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 02 November 2022, pp. 310-323
- Print publication:
- May 2023
-
- Article
- Export citation
Crofton formulas in pseudo-Riemannian space forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 28 October 2022, pp. 1935-1979
- Print publication:
- October 2022
-
- Article
- Export citation