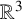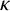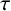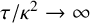Refine search
Actions for selected content:
27 results
9 - Geometry and dynamics in Yang–Mills matrix models
- from Part III - Noncommutative field theory and matrix models
-
- Book:
- Quantum Geometry, Matrix Theory, and Gravity
- Published online:
- 04 April 2024
- Print publication:
- 11 April 2024, pp 260-290
-
- Chapter
- Export citation
Torsion in classifying spaces of gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 01 April 2024, pp. 2224-2239
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTING THE TORSION OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 56-63
- Print publication:
- August 2024
-
- Article
- Export citation
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some asymptotic formulae for torsion in homotopy groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1339-1357
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 14 - Paediatric Clinical Cases
-
-
- Book:
- Orthopaedic Examination Techniques
- Published online:
- 22 April 2022
- Print publication:
- 12 May 2022, pp 252-267
-
- Chapter
- Export citation
Peri-operative myocardial performance in infants with Down syndrome undergoing CHD repair
- Part of
-
- Journal:
- Cardiology in the Young / Volume 32 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 960-968
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Truss, Temperature Effect, and Torsion
-
- Book:
- Finite Element Method for Solids and Structures
- Published online:
- 08 July 2021
- Print publication:
- 17 June 2021, pp 42-68
-
- Chapter
- Export citation
10 - Other Testing Geometries and Conditions
-
- Book:
- Testing of the Plastic Deformation of Metals
- Published online:
- 24 May 2021
- Print publication:
- 10 June 2021, pp 219-269
-
- Chapter
- Export citation
Load Ratios Carried by Each Constituent for Some Problems of a Particulate Composite Modeled as a Mixture of Two Linear Elastic Solids
-
- Journal:
- Journal of Mechanics / Volume 36 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 14 October 2020, pp. 857-865
- Print publication:
- December 2020
-
- Article
- Export citation
Maturational patterns of left ventricular rotational mechanics in pre-term infants through 1 year of age
-
- Journal:
- Cardiology in the Young / Volume 30 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 1238-1246
-
- Article
- Export citation
9 - Torsion of Prismatic Rods
- from Part II - Applications
-
- Book:
- Intermediate Solid Mechanics
- Published online:
- 16 December 2019
- Print publication:
- 09 January 2020, pp 259-306
-
- Chapter
- Export citation

Intermediate Solid Mechanics
-
- Published online:
- 16 December 2019
- Print publication:
- 09 January 2020
ON MODULES OVER COMMUTATIVE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 21 November 2017, pp. 341-356
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Riemannian surfaces with torsion as homogenization limits of locally Euclidean surfaces with dislocation-type singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 741-768
- Print publication:
- August 2016
-
- Article
- Export citation
Small Flag Complexes with Torsion
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-230
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
Left ventricular rotation and right–left ventricular interaction in congenital heart disease: the acute effects of interventional closure of patent arterial ducts and atrial septal defects*
-
- Journal:
- Cardiology in the Young / Volume 24 / Issue 4 / August 2014
- Published online by Cambridge University Press:
- 29 July 2013, pp. 661-674
-
- Article
- Export citation
Evaluation of left ventricular torsion in children with hypertrophic cardiomyopathy
-
- Journal:
- Cardiology in the Young / Volume 24 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 February 2013, pp. 245-252
-
- Article
- Export citation
Closed-Form Approximate Formulas for Torsional Analysis of Hollow Tubes with Straight and Circular Edges
-
- Journal:
- Journal of Mechanics / Volume 25 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 05 May 2011, pp. 401-409
- Print publication:
- December 2009
-
- Article
- Export citation
Atténuation du premier mode de torsion d'une structurepar un batteur gyroscopique
-
- Journal:
- Mechanics & Industry / Volume 10 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 23 July 2009, pp. 121-130
- Print publication:
- March 2009
-
- Article
- Export citation