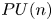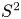1. Introduction
For a topological space $X$![]() , we say $X$
, we say $X$![]() has torsion if its integral homology does. Let $G$
has torsion if its integral homology does. Let $G$![]() be a compact connected Lie group. The cohomology of the connected Lie group $G$
be a compact connected Lie group. The cohomology of the connected Lie group $G$![]() , its loop space $\Omega G$
, its loop space $\Omega G$![]() and its classifying space $BG$
and its classifying space $BG$![]() has been studied by many mathematicians after the pioneering works of Hopf, Bott and Borel. The loop space $\Omega G$
has been studied by many mathematicians after the pioneering works of Hopf, Bott and Borel. The loop space $\Omega G$![]() has no torsion. The classifying space $BG$
has no torsion. The classifying space $BG$![]() has torsion if and only if $G$
has torsion if and only if $G$![]() does.
does.
Let $P\to X$![]() be a principal $G$
be a principal $G$![]() -bundle over a paracompact space $X$
-bundle over a paracompact space $X$![]() . Then, there is a classifying map $f\colon X\to BG$
. Then, there is a classifying map $f\colon X\to BG$![]() . The group of bundle automorphisms covering the identity on X is called the gauge group $\mathcal {G}(P)$
. The group of bundle automorphisms covering the identity on X is called the gauge group $\mathcal {G}(P)$![]() . The classifying space $B\mathcal {G}(P)$
. The classifying space $B\mathcal {G}(P)$![]() is homotopy equivalent to the path-component of the mapping space $\mathrm {Map}(X,\, BG)$
is homotopy equivalent to the path-component of the mapping space $\mathrm {Map}(X,\, BG)$![]() containing the classifying map $f$
containing the classifying map $f$![]() as in [Reference Atiyah and Bott1, Reference Gottlieb2]. If $X=S^1$
as in [Reference Atiyah and Bott1, Reference Gottlieb2]. If $X=S^1$![]() , since $\pi _1(BG)=\{0\}$
, since $\pi _1(BG)=\{0\}$![]() , the mapping space $\mathrm {Map}(S^1,\, BG)$
, the mapping space $\mathrm {Map}(S^1,\, BG)$![]() is path-connected and it has torsion if and only if $G$
is path-connected and it has torsion if and only if $G$![]() does. If $X=S^2$
does. If $X=S^2$![]() , since $\pi _2(BG)$
, since $\pi _2(BG)$![]() might not be zero, the mapping space $\mathrm {Map}(S^2,\, BG)$
might not be zero, the mapping space $\mathrm {Map}(S^2,\, BG)$![]() may not be path-connected. The path-component that contains the trivial map is homotopy equivalent to the classifying space of the gauge group of the trivial $G$
may not be path-connected. The path-component that contains the trivial map is homotopy equivalent to the classifying space of the gauge group of the trivial $G$![]() -bundle over $S^2$
-bundle over $S^2$![]() , and it has torsion if and only if $G$
, and it has torsion if and only if $G$![]() does. However, the situation is different for other path-components that are homotopy equivalent to classifying spaces of gauge groups of non-trivial $G$
does. However, the situation is different for other path-components that are homotopy equivalent to classifying spaces of gauge groups of non-trivial $G$![]() -bundles.
-bundles.
Let $SO(n)$![]() be the special orthogonal groups. Classification of $SO(n)$
be the special orthogonal groups. Classification of $SO(n)$![]() -bundles over $S^2$
-bundles over $S^2$![]() is determined by the Stiefel–Whitney class $w_2\in \mathbb {Z}/2=\{0,\,1\}=\pi _2(BSO(n))$
is determined by the Stiefel–Whitney class $w_2\in \mathbb {Z}/2=\{0,\,1\}=\pi _2(BSO(n))$![]() . The path-component of the mapping space corresponding to the non-trivial Stiefel–Whitney class is homotopy equivalent to the classifying space of the gauge group of the non-trivial $SO(n)$
. The path-component of the mapping space corresponding to the non-trivial Stiefel–Whitney class is homotopy equivalent to the classifying space of the gauge group of the non-trivial $SO(n)$![]() -bundle over $S^2$
-bundle over $S^2$![]() . Tsukuda [Reference Tsukuda5] showed that it has no torsion for $n=3$
. Tsukuda [Reference Tsukuda5] showed that it has no torsion for $n=3$![]() . Minowa [Reference Minowa3] proved that it has no torsion for $n=3,\,4$
. Minowa [Reference Minowa3] proved that it has no torsion for $n=3,\,4$![]() and torsion for $n\geq 5$
and torsion for $n\geq 5$![]() .
.
The special orthogonal group $SO(3)$![]() could be regarded as the projective unitary group $PU(2)=U(2)/S^1$
could be regarded as the projective unitary group $PU(2)=U(2)/S^1$![]() . In this paper, we generalize Tsukuda's result for projective unitary groups $PU(n)$
. In this paper, we generalize Tsukuda's result for projective unitary groups $PU(n)$![]() , $n\geq 2$
, $n\geq 2$![]() and determine when the classifying space of a $PU(n)$
and determine when the classifying space of a $PU(n)$![]() -gauge group over the sphere $S^2$
-gauge group over the sphere $S^2$![]() has torsion.
has torsion.
Throughout the rest of this paper, let $n$![]() be an integer greater than or equal to 2. The second homotopy group $\pi _2(BPU(n))$
be an integer greater than or equal to 2. The second homotopy group $\pi _2(BPU(n))$![]() is isomorphic to the cyclic group $\mathbb {Z}/n$
is isomorphic to the cyclic group $\mathbb {Z}/n$![]() . We identify the cyclic group $\mathbb {Z}/n$
. We identify the cyclic group $\mathbb {Z}/n$![]() with its complete set of representatives $\{ 0,\,1,\, \ldots,\, n-1\}$
with its complete set of representatives $\{ 0,\,1,\, \ldots,\, n-1\}$![]() . Let $k$
. Let $k$![]() be an element in
be an element in
Let us denote by $\mathrm {Map}_k(S^2,\, BPU(n))$![]() the path-component of the mapping space $\mathrm {Map}(S^2,\, BPU(n))$
the path-component of the mapping space $\mathrm {Map}(S^2,\, BPU(n))$![]() containing maps in the homotopy class $k$
containing maps in the homotopy class $k$![]() . Let $p$
. Let $p$![]() be a prime number. Unless explicitly stated, $H^{*}(X)$
be a prime number. Unless explicitly stated, $H^{*}(X)$![]() is the mod $p$
is the mod $p$![]() cohomology of the topological space $X$
cohomology of the topological space $X$![]() . The following is the $p$
. The following is the $p$![]() -local form of our result.
-local form of our result.
Theorem 1.1 The following holds for $\mathrm {Map}_k (S^2,\, BPU(n))$![]() .
.
(1) If $n\not \equiv 0 \mod (p)$
 , it has no $p$
, it has no $p$ -torsion.
-torsion.(2) If $n\equiv 0 \mod (p)$
 and $k\not \equiv 0\mod (p)$
and $k\not \equiv 0\mod (p)$ , it has no $p$
, it has no $p$ -torsion.
-torsion.(3) If $n\equiv 0 \mod (p)$
 and $k\equiv 0\mod (p)$
and $k\equiv 0\mod (p)$ , it has $p$
, it has $p$ -torsion.
-torsion.
As an immediate consequence of theorem 1.1, we obtain the following global form of our result.
Corollary 1.2 The topological space $\mathrm {Map}_k(S^2,\, BPU(n))$![]() has no torsion if and only if $k$
has no torsion if and only if $k$![]() is relatively prime to $n$
is relatively prime to $n$![]() .
.
In particular, for $n\geq 2$![]() , the topological space $\mathrm {Map}_1(S^2,\, BPU(n))$
, the topological space $\mathrm {Map}_1(S^2,\, BPU(n))$![]() has no torsion even though the underlying Lie group $PU(n)$
has no torsion even though the underlying Lie group $PU(n)$![]() has torsion.
has torsion.
This paper is organized as follows. In § 2, we show the existence of $p$![]() -torsion in $\mathrm {Map}_k(S^2,\, BPU(n))$
-torsion in $\mathrm {Map}_k(S^2,\, BPU(n))$![]() is equivalent to the triviality of certain induced homomorphism in the mod $p$
is equivalent to the triviality of certain induced homomorphism in the mod $p$![]() cohomology. Section 3 recalls the free double suspension in Takeda [Reference Takeda4] and its elementary properties. Section 4 collects some elementary facts on the mod $p$
cohomology. Section 3 recalls the free double suspension in Takeda [Reference Takeda4] and its elementary properties. Section 4 collects some elementary facts on the mod $p$![]() cohomology of $BU(n)$
cohomology of $BU(n)$![]() . In § 5, we prove theorem 1.1 assuming lemma 5.6 on an $n\times n$
. In § 5, we prove theorem 1.1 assuming lemma 5.6 on an $n\times n$![]() matrix $B$
matrix $B$![]() . In § 6, we prove lemma 5.6.
. In § 6, we prove lemma 5.6.
The author would like to thank Yuki Minowa for his talk on [Reference Minowa3] at the Homotopy Theory Symposium at the Osaka Metropolitan University on 5 November 2023. This work was inspired by his talk.
2. Torsion
In this section, we show that the existence of $p$![]() -torsion of a path-component is equivalent to the triviality of certain induced homomorphism.
-torsion of a path-component is equivalent to the triviality of certain induced homomorphism.
Let us fix a fibre bundle $BU(n)\to BPU(n)$![]() induced by the obvious projection map $U(n)\to PU(n)$
induced by the obvious projection map $U(n)\to PU(n)$![]() . We denote the inclusion map of its fibre by $\phi \colon BS^1 \to BU(n)$
. We denote the inclusion map of its fibre by $\phi \colon BS^1 \to BU(n)$![]() . It is a map induced by the obvious inclusion map $S^1 \to U(n)$
. It is a map induced by the obvious inclusion map $S^1 \to U(n)$![]() where $S^1$
where $S^1$![]() consists of the scalar matrices in the unitary group $U(n)$
consists of the scalar matrices in the unitary group $U(n)$![]() . Consider the commutative diagram induced by the fibre bundle $BU(n)\to BPU(n)$
. Consider the commutative diagram induced by the fibre bundle $BU(n)\to BPU(n)$![]() .
.

Both vertical maps in the bottom-right square are evaluation maps at the base point of $S^2$![]() , and all maps in the bottom-right square are fibrations. Moreover, all horizontal and vertical sequences are fibre sequences. In particular, $\Omega _k^2 BU(n)$
, and all maps in the bottom-right square are fibrations. Moreover, all horizontal and vertical sequences are fibre sequences. In particular, $\Omega _k^2 BU(n)$![]() and $\Omega _k^2 BPU(n)$
and $\Omega _k^2 BPU(n)$![]() are fibres of evaluation maps. Since
are fibres of evaluation maps. Since
is a homotopy equivalence, the fibre $F_0$![]() is contractible, and the map $F\to BS^1$
is contractible, and the map $F\to BS^1$![]() is also a homotopy equivalence.
is also a homotopy equivalence.
The goal of this section is to prove the following proposition.
Proposition 2.1 The following are equivalent.
(1) The topological space $\mathrm {Map}_k(S^2,\, BPU(n))$
 has $p$
has $p$ -torsion.
-torsion.(2) The mod $p$
 cohomology of $\mathrm {Map}_k(S^2,\, BPU(n))$
cohomology of $\mathrm {Map}_k(S^2,\, BPU(n))$ has a non-zero odd degree element.
has a non-zero odd degree element.(3) The induced homomorphism $\varphi ^{*}\colon H^2(\mathrm {Map}_k(S^2,\, BU(n)))\to H^2(F)$
 is zero.
is zero.
To establish the equivalence of (1) and (2) in proposition 2.1, we use the following lemma.
Lemma 2.2 Let $X$![]() be a topological space. Suppose that the integral homology groups $H_i(X;\mathbb {Z})$
be a topological space. Suppose that the integral homology groups $H_i(X;\mathbb {Z})$![]() are finitely generated abelian groups for all $i$
are finitely generated abelian groups for all $i$![]() , and the rational cohomology of $X$
, and the rational cohomology of $X$![]() has no non-zero odd degree element. Then, the mod $p$
has no non-zero odd degree element. Then, the mod $p$![]() cohomology $H^{*}(X;\mathbb {Z}/p)$
cohomology $H^{*}(X;\mathbb {Z}/p)$![]() has a non-zero odd degree element if and only if $X$
has a non-zero odd degree element if and only if $X$![]() has $p$
has $p$![]() -torsion.
-torsion.
Proof. First, we prove that the assumptions of lemma 2.2 imply that $H_{2j+1}(X;\mathbb {Z})$![]() is a finite abelian group for all $j$
is a finite abelian group for all $j$![]() . By the universal coefficient theorem, we have an isomorphism
. By the universal coefficient theorem, we have an isomorphism
By the assumption that the rational cohomology of $X$![]() has no non-zero odd degree element, we have
has no non-zero odd degree element, we have
By the assumption that the integral homology groups $H_{i}(X;\mathbb {Z})$![]() are finitely generated, $H_{2j+1}(X;\mathbb {Z})$
are finitely generated, $H_{2j+1}(X;\mathbb {Z})$![]() is a finite abelian group.
is a finite abelian group.
Next, we show that if $X$![]() has $p$
has $p$![]() -torsion, then $H^{2j+1}(X;\mathbb {Z}/p)$
-torsion, then $H^{2j+1}(X;\mathbb {Z}/p)$![]() is non-trivial for some $j$
is non-trivial for some $j$![]() . By the universal coefficient theorem, we have an isomorphism
. By the universal coefficient theorem, we have an isomorphism
If $X$![]() has $p$
has $p$![]() -torsion, $H_{2j+1}(X;\mathbb {Z})$
-torsion, $H_{2j+1}(X;\mathbb {Z})$![]() or $H_{2j}(X;\mathbb {Z})$
or $H_{2j}(X;\mathbb {Z})$![]() has $p$
has $p$![]() -torsion for some $j$
-torsion for some $j$![]() . Therefore, $H^{2j+1}(X;\mathbb {Z}/p)$
. Therefore, $H^{2j+1}(X;\mathbb {Z}/p)$![]() is non-trivial.
is non-trivial.
Finally, we show that if $H^{2j+1}(X;\mathbb {Z}/p)$![]() is non-trivial for some $j$
is non-trivial for some $j$![]() , $X$
, $X$![]() has $p$
has $p$![]() -torsion. By the universal coefficient theorem, we have an isomorphism
-torsion. By the universal coefficient theorem, we have an isomorphism
Suppose that
is non-trivial. Then, since $H_{2j+1}(X;\mathbb {Z})$![]() is a finite abelian group, $H_{2j+1}(X;\mathbb {Z})$
is a finite abelian group, $H_{2j+1}(X;\mathbb {Z})$![]() has $p$
has $p$![]() -torsion. Suppose that
-torsion. Suppose that
is non-trivial. Then, since $H_{2j}(X;\mathbb {Z})$![]() is a finitely generated abelian group, $H_{2j}(X;\mathbb {Z})$
is a finitely generated abelian group, $H_{2j}(X;\mathbb {Z})$![]() has $p$
has $p$![]() -torsion. Hence, in either case, $X$
-torsion. Hence, in either case, $X$![]() has $p$
has $p$![]() -torsion.
-torsion.
Proof Proof of proposition 2.1, (1) $\Leftrightarrow$![]() (2)
(2)
Let us consider the right vertical fibre sequence
and Leray–Serre spectral sequences associated with this fibre sequence. The $E_2$![]() -page of the Leray–Serre spectral sequence for the integral homology consists of finitely generated abelian groups, and so are the integral homology groups of $\mathrm {Map}_k(S^2,\, BPU(n))$
-page of the Leray–Serre spectral sequence for the integral homology consists of finitely generated abelian groups, and so are the integral homology groups of $\mathrm {Map}_k(S^2,\, BPU(n))$![]() . The $E_2$
. The $E_2$![]() -page of the Leray–Serre spectral sequence for the rational cohomology has no non-zero odd degree element. So the rational cohomology of $\mathrm {Map}_k(S^2,\, BPU(n))$
-page of the Leray–Serre spectral sequence for the rational cohomology has no non-zero odd degree element. So the rational cohomology of $\mathrm {Map}_k(S^2,\, BPU(n))$![]() also has no non-zero odd degree element. Thus, by lemma 2.2, $\mathrm {Map}_k(S^2,\, BPU(n))$
also has no non-zero odd degree element. Thus, by lemma 2.2, $\mathrm {Map}_k(S^2,\, BPU(n))$![]() has $p$
has $p$![]() -torsion if and only if its mod $p$
-torsion if and only if its mod $p$![]() cohomology has a non-zero odd degree element.
cohomology has a non-zero odd degree element.
Let $c_i\in H^{2i}(BU(n))$![]() be the mod $p$
be the mod $p$![]() reduction of the $i^{\mathrm {th}}$
reduction of the $i^{\mathrm {th}}$![]() Chern class. The following proposition is what we need on the mod $p$
Chern class. The following proposition is what we need on the mod $p$![]() cohomology of $\mathrm {Map}_k(S^2,\, BU(n))$
cohomology of $\mathrm {Map}_k(S^2,\, BU(n))$![]() in this section. Section 5 gives a more detailed description of the generator $x$
in this section. Section 5 gives a more detailed description of the generator $x$![]() in terms of $c_2$
in terms of $c_2$![]() and the free double suspension we will define in § 3.
and the free double suspension we will define in § 3.
Proposition 2.3 The following hold.
(1) $H^{*}(\mathrm {Map}_k(S^2,\, BU(n)))$
 has no non-zero odd degree element.
has no non-zero odd degree element.(2) As an abelian group, $H^{2}(\mathrm {Map}_k(S^2,\, BU(n)))$
 is generated by two elements $\pi ^*(c_1)$
is generated by two elements $\pi ^*(c_1)$ and $x$
and $x$ such that $\iota _k^*(x)\not =0$
such that $\iota _k^*(x)\not =0$ .
.
Proof. Consider the Leray–Serre spectral sequence associated with the middle vertical fibre sequence
converging to the mod $p$![]() cohomology of $\mathrm {Map}_k(S^2,\, BU(n))$
cohomology of $\mathrm {Map}_k(S^2,\, BU(n))$![]() . Then, the $E_2$
. Then, the $E_2$![]() -page has no non-zero odd degree element. Hence, the spectral sequence collapses at the $E_2$
-page has no non-zero odd degree element. Hence, the spectral sequence collapses at the $E_2$![]() -page, and we obtain (1). Furthermore, we have
-page, and we obtain (1). Furthermore, we have

Hence, we have (2).
Proof Proof of proposition 2.1, (2) $\Leftrightarrow$![]() (3)
(3)
We consider the Leray–Serre spectral sequence associated with the middle horizontal fibre sequence
converging to the mod $p$![]() cohomology of $\mathrm {Map}_k ( S^2,\, BU(n))$
cohomology of $\mathrm {Map}_k ( S^2,\, BU(n))$![]() . The mod $p$
. The mod $p$![]() cohomology ring of $F\simeq BS^1$
cohomology ring of $F\simeq BS^1$![]() is a polynomial ring generated by a single element $u$
is a polynomial ring generated by a single element $u$![]() of degree $2$
of degree $2$![]() . The $E_2$
. The $E_2$![]() -page is given by
-page is given by
If the induced homomorphism
is non-zero, the induced homomorphism
is surjective. Then, by the Leray–Hirsh theorem, the induced homomorphism
is injective and, by proposition 2.3 (1), the mod $p$![]() cohomology of $\mathrm {Map}_{k}(S^2,\, BPU(n))$
cohomology of $\mathrm {Map}_{k}(S^2,\, BPU(n))$![]() also has no non-zero odd degree element.
also has no non-zero odd degree element.
If the induced homomorphism
is zero, $u$![]() does not survive to the $E_\infty$
does not survive to the $E_\infty$![]() -page. Hence, $d_2(u)\not =0$
-page. Hence, $d_2(u)\not =0$![]() or $d_3(u)\not =0$
or $d_3(u)\not =0$![]() must hold. Relevant subgroups of $E_2$
must hold. Relevant subgroups of $E_2$![]() -page are as follows.
-page are as follows.

Since $d_2(u)\in E_2^{2,1}=\{0\}$![]() , we have $d_2(u)=0$
, we have $d_2(u)=0$![]() . Therefore, $d_3(u)\not =0$
. Therefore, $d_3(u)\not =0$![]() . Since $E_2^{1,1}=\{0\}$
. Since $E_2^{1,1}=\{0\}$![]() , the differential $d_2\colon E_2^{1,1}\to E_2^{3,0}$
, the differential $d_2\colon E_2^{1,1}\to E_2^{3,0}$![]() is zero and we have $E_3^{3,0}=E_2^{3,0}$
is zero and we have $E_3^{3,0}=E_2^{3,0}$![]() . Since
. Since
is non-zero, the mod $p$![]() cohomology of $\mathrm {Map}_{k}(S^2,\, BPU(n))$
cohomology of $\mathrm {Map}_{k}(S^2,\, BPU(n))$![]() has the non-zero odd degree element $d_3(u)$
has the non-zero odd degree element $d_3(u)$![]() .
.
3. Free double suspension
To describe the generator $x$![]() of $H^2(\mathrm {Map}_k(S^2,\, BU(n)))$
of $H^2(\mathrm {Map}_k(S^2,\, BU(n)))$![]() in proposition 2.3 in more detail, we use the free double suspension
in proposition 2.3 in more detail, we use the free double suspension
defined by Takeda in [Reference Takeda4]. One may define the free double suspension over any coefficient groups. We focus on the mod $p$![]() cohomology. Our definition of $\sigma$
cohomology. Our definition of $\sigma$![]() differs slightly from Takeda's $\hat {\sigma }_f^2$
differs slightly from Takeda's $\hat {\sigma }_f^2$![]() in [Reference Takeda4] but is the same homomorphism.
in [Reference Takeda4] but is the same homomorphism.
In this section, let $X$![]() be a simply connected topological space. We denote by $*$
be a simply connected topological space. We denote by $*$![]() the base points of both $S^2$
the base points of both $S^2$![]() and $X$
and $X$![]() . Let $k$
. Let $k$![]() be a homotopy class in $\pi _2(X)$
be a homotopy class in $\pi _2(X)$![]() and $0$
and $0$![]() is the homotopy class in $\pi _2(X)$
is the homotopy class in $\pi _2(X)$![]() containing the trivial map. Let
containing the trivial map. Let
be the obvious projection map. We use the evaluation maps
and its restriction to $\mathrm {Map}_k(S^2,\, X)=\{*\} \times \mathrm {Map}_k(S^2,\, X)$![]() ,
,
to define a homomorphism
Let us fix a generator of $H^2(S^2)\simeq \mathbb {Z}/p$![]() and we denote it by $u_2$
and we denote it by $u_2$![]() . We define $\sigma$
. We define $\sigma$![]() by
by
Let $\Omega _k^2 X=\pi ^{-1}(*)$![]() and denote the inclusion map by $\iota _k\colon \Omega _k^2 X\to \mathrm {Map}_k(S^2,\, X)$
and denote the inclusion map by $\iota _k\colon \Omega _k^2 X\to \mathrm {Map}_k(S^2,\, X)$![]() . We define
. We define
by $\iota _k^* \circ \sigma$![]() . Proposition 3.1 (1) below is nothing but a particular form of proposition 2.1 in [Reference Takeda4].
. Proposition 3.1 (1) below is nothing but a particular form of proposition 2.1 in [Reference Takeda4].
Proposition 3.1 The homomorphism $\sigma$![]() satisfies the following.
satisfies the following.
(1) $\sigma (x \cdot y) =\sigma (x) \cdot \pi ^{*}(y)+\pi ^{*}(x) \cdot \sigma (y)$
 ,
,(2) for a cohomology operation $\mathcal {O}$
 of positive degree, $\sigma (\mathcal {O} x)=\mathcal {O}\sigma (x)$
of positive degree, $\sigma (\mathcal {O} x)=\mathcal {O}\sigma (x)$ .
.
Proof.
(1) Since
\begin{align*} \mathrm{ev}^{*}(x) \cdot \mathrm{ev}^{*}(y)& =(u_2 \otimes \sigma(x) +1\otimes \pi^{*}(x))\cdot (u_2 \otimes \sigma(y) +1\otimes \pi^{*}(y)) \\ & = u_2 \otimes \sigma(x) \cdot 1\otimes \pi^{*}(y)\\ & \quad + 1\otimes \pi^{*}(x) \cdot u_2 \otimes \sigma(y)+1\otimes \pi^{*}(x)\cdot 1\otimes \pi^{*}(y) \\ & =u_2 \otimes (\sigma(x)\cdot \pi^{*}(y)+\pi^{*}(x) \cdot \sigma(y))+1 \otimes (\pi^{*}(x)\cdot \pi^{*}(y)), \end{align*}Hence, we have \[ \mathrm{ev}^{*}(x\cdot y)-(\pi\circ \mathrm{pr}_2)^*(x\cdot y)=u_2 \otimes (\sigma(x)\cdot \pi^{*}(y)+\pi^{*}(x) \cdot \sigma(y)). \]
\[ \mathrm{ev}^{*}(x\cdot y)-(\pi\circ \mathrm{pr}_2)^*(x\cdot y)=u_2 \otimes (\sigma(x)\cdot \pi^{*}(y)+\pi^{*}(x) \cdot \sigma(y)). \]
(2) is also clear from the naturality of cohomology operation.
\begin{align*} \mathcal{O} (\mathrm{ev}^{*}(x)-(\pi\circ \mathrm{pr}_2)^{*}(x))& =\mathrm{ev}^{*}(\mathcal{O}x)-(\pi\circ \mathrm{pr}_2)^{*}(\mathcal{O}x) \\ & =u_2 \otimes \sigma(\mathcal{O}x),\\ \mathcal{O}(u_2\otimes \sigma(x))& =u_2 \otimes \mathcal{O}\sigma(x), \end{align*}since $\mathcal {O} u_2=0$
 . Hence, we have
\[ \sigma(\mathcal{O}x)=\mathcal{O}\sigma(x). \]□
. Hence, we have
\[ \sigma(\mathcal{O}x)=\mathcal{O}\sigma(x). \]□
Next, we describe the relation between $\Omega _k^2 X$![]() and $\Omega _0^2 X$
and $\Omega _0^2 X$![]() . Let $X_1\vee X_2$
. Let $X_1\vee X_2$![]() be the subspace of $X_1 \times X_2$
be the subspace of $X_1 \times X_2$![]() defined by
defined by
Let $\nu \colon S^2 \to S^2 \vee S^2$![]() be the pinch map collapsing the sphere's equator. We use it to define the addition on $\pi _2(X)$
be the pinch map collapsing the sphere's equator. We use it to define the addition on $\pi _2(X)$![]() . Let $f\colon S^2\to X$
. Let $f\colon S^2\to X$![]() be a map representing $k\in \pi _2(X)$
be a map representing $k\in \pi _2(X)$![]() and $\mathrm {c}_f\colon \Omega _0^2 X\to \{ f\}$
and $\mathrm {c}_f\colon \Omega _0^2 X\to \{ f\}$![]() the obvious constant map. Using $f$
the obvious constant map. Using $f$![]() , we define
, we define
by
The following lemma is a weak form of lemma 2.2 in [Reference Takeda4]. We use it to prove proposition 5.1.
Lemma 3.2 Let $x$![]() be an element in $H^{i}(X)$
be an element in $H^{i}(X)$![]() . If $i\not =2$
. If $i\not =2$![]() , then we have
, then we have
Proof. We have the following commutative diagram by the definition of $\mu _f$![]() .
.

where we choose $f$![]() as the base point of both $\{ f\}$
as the base point of both $\{ f\}$![]() and $\Omega _k^2 X$
and $\Omega _k^2 X$![]() , and the constant map $S^2\to \{*\}$
, and the constant map $S^2\to \{*\}$![]() as the base point of $\Omega _0^2X$
as the base point of $\Omega _0^2X$![]() . Since the reduced mod $p$
. Since the reduced mod $p$![]() cohomology $\widetilde {H}^{i}(S^2\times \{f\})\simeq \widetilde {H}^{i}(S^2)$
cohomology $\widetilde {H}^{i}(S^2\times \{f\})\simeq \widetilde {H}^{i}(S^2)$![]() is trivial for $i\not =2$
is trivial for $i\not =2$![]() , we have isomorphisms
, we have isomorphisms
and desired identity
for $x\in H^i(X)$![]() , $i\not =2$
, $i\not =2$![]() .
.
4. Cohomology of $BU(n)$
In this section, we collect some elementary properties of the mod $p$![]() cohomology ring of $BU(n)$
cohomology ring of $BU(n)$![]() and the induced homomorphism
and the induced homomorphism
Let us fix a generator $u$![]() of $H^2(BU(1))=H^2(BS^1)\simeq \mathbb {Z}/p$
of $H^2(BU(1))=H^2(BS^1)\simeq \mathbb {Z}/p$![]() . Let
. Let
be the map induced by the inclusion map of the maximal torus $U(1)^n$![]() consisting of diagonal matrices. Let
consisting of diagonal matrices. Let
be the map induced by the projection of $U(1)^n$![]() to its $i^{\mathrm {th}}$
to its $i^{\mathrm {th}}$![]() factor $U(1)$
factor $U(1)$![]() , defined by $(x_1,\, \dots,\, x_n)\mapsto x_i$
, defined by $(x_1,\, \dots,\, x_n)\mapsto x_i$![]() . We denote $B\mathrm {pr}_i^{*}(u)\in H^2(BU(1)^n)$
. We denote $B\mathrm {pr}_i^{*}(u)\in H^2(BU(1)^n)$![]() by $t_i$
by $t_i$![]() . The mod $p$
. The mod $p$![]() cohomology of $BU(1)^n$
cohomology of $BU(1)^n$![]() is a polynomial ring generated by $t_1,\, \ldots,\, t_n$
is a polynomial ring generated by $t_1,\, \ldots,\, t_n$![]() and the induced homomorphism
and the induced homomorphism
is injective, and its image is the set of symmetric polynomials in $t_1,\, \ldots,\, t_n$![]() . In particular, $c_i$
. In particular, $c_i$![]() is defined as the element such that $\iota ^{*}(c_i)$
is defined as the element such that $\iota ^{*}(c_i)$![]() is the $i^{\mathrm {th}}$
is the $i^{\mathrm {th}}$![]() elementary symmetric polynomial in $t_1,\, \ldots,\, t_n$
elementary symmetric polynomial in $t_1,\, \ldots,\, t_n$![]() . Let us define $s_i$
. Let us define $s_i$![]() by
by

The map $\phi \colon BS^1 \to BU(n)$![]() factors through
factors through
where $\delta$![]() is the map induced by the diagonal map $x\mapsto (x,\,\ldots,\, x)$
is the map induced by the diagonal map $x\mapsto (x,\,\ldots,\, x)$![]() . Since $\delta ^{*}(t_i)=u$
. Since $\delta ^{*}(t_i)=u$![]() for $i=1,\, \ldots,\, n$
for $i=1,\, \ldots,\, n$![]() , we have
, we have
and
We use the following lemma 4.1 to prove proposition 5.5. The corresponding identity in symmetric polynomials is known as Newton's identity.
Lemma 4.1 In the mod $p$![]() cohomology of $BU(n)$
cohomology of $BU(n)$![]() , for $i\geq 0$
, for $i\geq 0$![]() , we have relations
, we have relations

Proof. Let us define symmetric polynomials $h_{i+2,n-1},\, \ldots,\, h_{n+i,1}$![]() . For $\ell =i+2,\,\ldots,\, n+i$
. For $\ell =i+2,\,\ldots,\, n+i$![]() , let $h_{\ell, n+i+1-\ell }$
, let $h_{\ell, n+i+1-\ell }$![]() be the sum of monomials in the polynomial ring $\mathbb {Z}/p[t_1,\, \ldots,\, t_n]$
be the sum of monomials in the polynomial ring $\mathbb {Z}/p[t_1,\, \ldots,\, t_n]$![]() obtained from $t_1^{\ell } t_2 \cdots t_{n+i+2-\ell }$
obtained from $t_1^{\ell } t_2 \cdots t_{n+i+2-\ell }$![]() by permuting $1,\, \ldots,\, n+j+2-\ell$
by permuting $1,\, \ldots,\, n+j+2-\ell$![]() in $1,\, \ldots,\, n$
in $1,\, \ldots,\, n$![]() . Then, we have
. Then, we have

Therefore, we have

Since $\iota ^*$![]() is injective, it completes the proof.
is injective, it completes the proof.
If $p$![]() is an odd prime, let
is an odd prime, let
be the $i^{\mathrm {th}}$![]() Steenrod reduced power. If $p=2$
Steenrod reduced power. If $p=2$![]() , let $\wp ^1=\mathrm {Sq}^2$
, let $\wp ^1=\mathrm {Sq}^2$![]() and $\wp ^{2^{\ell -1}}= \mathrm {Sq}^{2^\ell }$
and $\wp ^{2^{\ell -1}}= \mathrm {Sq}^{2^\ell }$![]() for $\ell \geq 2$
for $\ell \geq 2$![]() , where
, where
is the $i^{\mathrm {th}}$![]() Steenrod square. We define cohomology operations $\mathcal {Q}_\ell$
Steenrod square. We define cohomology operations $\mathcal {Q}_\ell$![]() inductively by $\mathcal {Q}_1=\wp ^1$
inductively by $\mathcal {Q}_1=\wp ^1$![]() ,
,
for $\ell \geq 2$![]() . Cohomology operations $\mathcal {Q}_\ell$
. Cohomology operations $\mathcal {Q}_\ell$![]() have the following properties
have the following properties
(1) $\mathcal {Q}_{\ell }(x\cdot y)=\mathcal {Q}_{\ell }(x)\cdot y+x\cdot \mathcal {Q}_{\ell }( y)$
 for $x,\, y\in H^{*}(BU(1)^n)$
for $x,\, y\in H^{*}(BU(1)^n)$ ,
,(2) $\mathcal {Q}_{\ell } t_i=t_i^{p^\ell }$
 for $t_1,\, \ldots,\, t_n$
for $t_1,\, \ldots,\, t_n$ in $H^2(BU(1)^n)$
in $H^2(BU(1)^n)$ .
.
With these properties, we have the following lemma 4.2. We will use it to prove proposition 5.2.
Lemma 4.2 In the mod $p$![]() cohomology of $BU(n)$
cohomology of $BU(n)$![]() , for $\ell \geq 1$
, for $\ell \geq 1$![]() , we have
, we have
Proof. On the one hand, since
by direct calculation, we have
On the other hand, we have

Hence, we obtain the desired identity.
5. Proof of theorem 1.1
In this section, we consider the commutative diagram

We begin with the following refinement of proposition 2.3 (2).
Proposition 5.1 As an abelian group, $H^{2}(\mathrm {Map}_k(S^2,\, BU(n)))$![]() is generated by $\pi ^*(c_1)$
is generated by $\pi ^*(c_1)$![]() and $\sigma (c_2)$
and $\sigma (c_2)$![]() .
.
Proof. Let $\lambda \colon BSU(n)\to BU(n)$![]() and $\lambda '\colon \Omega ^2 BSU(n) \to \Omega ^2_0 BU(n)$
and $\lambda '\colon \Omega ^2 BSU(n) \to \Omega ^2_0 BU(n)$![]() be maps induced by the inclusion map $SU(n)\to U(n)$
be maps induced by the inclusion map $SU(n)\to U(n)$![]() . We have the following commutative diagram by lemma 2.2 and the naturality of cohomology suspension.
. We have the following commutative diagram by lemma 2.2 and the naturality of cohomology suspension.

The top horizontal homomorphism $\tilde {\sigma }$![]() is the composition of cohomology suspensions
is the composition of cohomology suspensions
and it is an isomorphism. Since $H^4(BSU(n))\simeq \mathbb {Z}/p$![]() is generated by $\lambda ^{*}(c_2)$
is generated by $\lambda ^{*}(c_2)$![]() , we have
, we have
Therefore, we obtain
By proposition 2.3 (2), $\pi ^{*}(c_1)$![]() and $\sigma (c_2)$
and $\sigma (c_2)$![]() generate $H^{2}(\mathrm {Map}_k(S^2,\, BU(n)))$
generate $H^{2}(\mathrm {Map}_k(S^2,\, BU(n)))$![]() .
.
Let $u\in H^2(F)=H^2(BS^1)\simeq \mathbb {Z}/p$![]() be the generator fixed in § 4. Let us define $\alpha _i,\, \beta \in \mathbb {Z}/p$
be the generator fixed in § 4. Let us define $\alpha _i,\, \beta \in \mathbb {Z}/p$![]() by
by

Proposition 5.2 If $n\equiv 0 \mod (p)$![]() , we have $\beta =-\alpha _{p^{\ell }}$
, we have $\beta =-\alpha _{p^{\ell }}$![]() for $\ell \geq 1$
for $\ell \geq 1$![]() .
.
Proof. On the one hand, by the definition of $\beta$![]() , we have
, we have
Applying $\mathcal {Q}_\ell$![]() , we have
, we have
On the other hand, by lemma 4.2, in the mod $p$![]() cohomology of $BU(n)$
cohomology of $BU(n)$![]() , we have the relation
, we have the relation
Applying $\varphi ^{*}\circ \sigma$![]() , we have
, we have

Hence, we have $\beta =-\alpha _{p^{\ell }}.$![]()
Summing up propositions 5.1 and 5.2, we have the following proposition 5.3. It reduces the proof of theorem 1.1 to the computation of $\alpha _p$![]() .
.
Proposition 5.3 The following are equivalent.
(1) $\varphi ^{*}\colon H^{2}(\mathrm {Map}_k(S^2,\, BU(n)))\to H^{2}(F)$
 is zero,
is zero,(2) $\phi ^{*}(c_1)=0$
 and $\beta =0$
and $\beta =0$ ,
,(3) $\phi ^{*}(c_1)=0$
 and $\alpha _p=0$
and $\alpha _p=0$ .
.
Proof. Since $H^{2}(\mathrm {Map}_k(S^2,\, BU(n)))$![]() is generated by $\pi ^{*}(c_1)$
is generated by $\pi ^{*}(c_1)$![]() and $\sigma (c_2)$
and $\sigma (c_2)$![]() , (1) and (2) are equivalent. Under the assumption that $\phi ^*(c_1)=0$
, (1) and (2) are equivalent. Under the assumption that $\phi ^*(c_1)=0$![]() , we have $n\equiv 0 \mod (p)$
, we have $n\equiv 0 \mod (p)$![]() . Then, by proposition 5.2, we have
. Then, by proposition 5.2, we have
Hence, (2) and (3) are equivalent.
By computing $\alpha _p$![]() , we complete the proof of theorem 1.1.
, we complete the proof of theorem 1.1.
Proposition 5.4 We have $\alpha _0=k$![]() .
.
Proof. Let $f\colon S^2\to BU(n) \in \mathrm {Map}_k(S^2,\, BU(n))$![]() . By definition, we have
. By definition, we have
Let
be a map defined by $t\mapsto (t,\,f)$![]() . Then, we have
. Then, we have
and
is a constant map $S^2\to \{ f(*) \}$![]() . It implies that
. It implies that
When we restrict $\mathrm {i}_f^*$![]() to $H^{2}((S^2,\, *) \times \mathrm {Map}_k(S^2,\, BU(n)))$
to $H^{2}((S^2,\, *) \times \mathrm {Map}_k(S^2,\, BU(n)))$![]() , it is injective. So, we have
, it is injective. So, we have
Hence, by the definition of $\sigma$![]() , we have $\sigma (c_1)=k$
, we have $\sigma (c_1)=k$![]() .
.
Proposition 5.5 If $n\equiv 0 \mod (p)$![]() , we have $\alpha _{p}=k$
, we have $\alpha _{p}=k$![]() .
.
We use the following lemma 5.6 to prove proposition 5.5. We will prove it in the next section. Let $B$![]() be an $n\times n$
be an $n\times n$![]() matrix whose $(i,\,j)$
matrix whose $(i,\,j)$![]() -entry is given by integers
-entry is given by integers
for $1\leq j\leq n$![]() and $b_{i,j}=1$
and $b_{i,j}=1$![]() if $i=j+1$
if $i=j+1$![]() , $b_{i,j}=0$
, $b_{i,j}=0$![]() if $i\not =j+1$
if $i\not =j+1$![]() for $2\leq i \leq n$
for $2\leq i \leq n$![]() , $1\leq j \leq n$
, $1\leq j \leq n$![]() .
.
Lemma 5.6 When we regard the matrix $B$![]() as an element in $SL_n(\mathbb {Z}/p)$
as an element in $SL_n(\mathbb {Z}/p)$![]() , the order of $B$
, the order of $B$![]() is a power of $p$
is a power of $p$![]() .
.
Proof Proof of proposition 5.5
By lemma 4.1, in $H^{*}(BU(n))$![]() , we have
, we have

for $i\geq 0$![]() . Applying $\varphi ^{*}\circ \sigma$
. Applying $\varphi ^{*}\circ \sigma$![]() , we have
, we have

Since $\phi ^{*}(s_{n+i-j+1})=0$![]() , we obtain
, we obtain

Furthermore, since $\displaystyle \phi ^*(c_j)=\binom{n}{j} u^j$![]() , we have
, we have

Thus, we have

Therefore, put these identities together in matrix form, using the $n\times n$![]() matrix $B$
matrix $B$![]() that we just defined, we have
that we just defined, we have

for $i\geq 0$![]() . By lemma 5.6, the order of $B$
. By lemma 5.6, the order of $B$![]() as an element of $SL_n(\mathbb {Z}/p)$
as an element of $SL_n(\mathbb {Z}/p)$![]() is a power of $p$
is a power of $p$![]() . Hence, for some positive integer $\ell$
. Hence, for some positive integer $\ell$![]() , we have
, we have
By proposition 5.2, we have $\alpha _{p^\ell }=-\beta =\alpha _p$![]() . Therefore, we obtain $\alpha _p=k$
. Therefore, we obtain $\alpha _p=k$![]() .
.
Proposition 5.7 below is immediate from proposition 5.5 and it completes the proof of theorem 1.1.
Proposition 5.7 The following holds.
(1) If $n\not \equiv 0 \mod (p)$
 , then $\phi ^{*}(c_1)\not =0$
, then $\phi ^{*}(c_1)\not =0$ ,
,(2) If $n\equiv 0 \mod (p)$
 and $k\not \equiv 0 \mod (p)$
and $k\not \equiv 0 \mod (p)$ , then $\alpha _p \not =0$
, then $\alpha _p \not =0$ ,
,(3) If $n\equiv 0 \mod (p)$
 and $k\equiv 0 \mod (p)$
and $k\equiv 0 \mod (p)$ , then $\phi ^{*}(c_1)=0$
, then $\phi ^{*}(c_1)=0$ and $\alpha _p=0$
and $\alpha _p=0$ .
.
6. Proof of lemma 5.6
In this section, we deal with unimodular $n\times n$![]() matrices. Unless otherwise clear from the context, matrix entries are integers. What we do in what follows is to find the transpose of the Jordan matrix similar to the matrix $B$
matrices. Unless otherwise clear from the context, matrix entries are integers. What we do in what follows is to find the transpose of the Jordan matrix similar to the matrix $B$![]() in § 5.
in § 5.
Proposition 6.1 There is a unimodular $n\times n$![]() matrix $A$
matrix $A$![]() such that $A^{-1}BA=D$
such that $A^{-1}BA=D$![]() where $(i,\,j)$
where $(i,\,j)$![]() -entry $d_{i,j}$
-entry $d_{i,j}$![]() of $D$
of $D$![]() is $d_{i,j}=1$
is $d_{i,j}=1$![]() if $i=j$
if $i=j$![]() or $i=j+1$
or $i=j+1$![]() and $d_{i,j}=0$
and $d_{i,j}=0$![]() if otherwise.
if otherwise.
We prove this proposition by giving such a matrix $A$![]() explicitly. Before we do it, we complete the proof of lemma 5.6.
explicitly. Before we do it, we complete the proof of lemma 5.6.
Proof Proof of lemma 5.6
By proposition 6.1, we have
The matrix $D$![]() belongs to the subgroup $U_n$
belongs to the subgroup $U_n$![]() of $SL_n(\mathbb {Z}/p)$
of $SL_n(\mathbb {Z}/p)$![]() consisting of lower triangular matrices whose diagonal entries are $1$
consisting of lower triangular matrices whose diagonal entries are $1$![]() . The subgroup $U_n$
. The subgroup $U_n$![]() is a $p$
is a $p$![]() -group. Therefore, the order of $D$
-group. Therefore, the order of $D$![]() is a power of $p$
is a power of $p$![]() . Hence, the order of $B$
. Hence, the order of $B$![]() is also the power of $p$
is also the power of $p$![]() .
.
Now, we prove proposition 6.1 by defining $A$![]() explicitly.
explicitly.
Proof Proof of proposition 6.1
Let $A$![]() be the $n\times n$
be the $n\times n$![]() unimodular upper triangular matrix whose $(i,\,j)$
unimodular upper triangular matrix whose $(i,\,j)$![]() -entry is given by
-entry is given by
We show that $(i,\,j)$![]() -entries of $BA$
-entries of $BA$![]() and $AD$
and $AD$![]() are equal to $\binom{n-i+1}{n-j}$
are equal to $\binom{n-i+1}{n-j}$![]() for $1\leq i\leq n,\, 1\leq j\leq n$
for $1\leq i\leq n,\, 1\leq j\leq n$![]() .
.
Recall that $B$![]() is the $n\times n$
is the $n\times n$![]() unimodular matrix whose $(i,\,j)$
unimodular matrix whose $(i,\,j)$![]() -entry is given as follows: For $i=1$
-entry is given as follows: For $i=1$![]() , $1\leq j \leq n$
, $1\leq j \leq n$![]() , the $(1,\,j)$
, the $(1,\,j)$![]() -entry of $B$
-entry of $B$![]() is given by
is given by
and, for $2\leq i \leq n$![]() , $1\leq j \leq n$
, $1\leq j \leq n$![]() , the $(i,\,j)$
, the $(i,\,j)$![]() -entry of $B$
-entry of $B$![]() is given by
is given by
(1) For $1\leq j\leq n$
 , the $(1,\,j)$
, the $(1,\,j)$ -entry of $BA$
-entry of $BA$ is given by
\begin{align*} \sum_{\ell=1}^n b_{1,\ell} a_{\ell,j} & =\sum_{\ell=1}^j b_{1,\ell} a_{\ell,j} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \binom{n}{\ell} \cdot \binom{n-\ell}{n-j} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \dfrac{n!}{(n-\ell)! \ell!} \cdot \dfrac{(n-\ell)!}{(n-j)!(j-\ell)!} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \dfrac{n!}{(n-j)! j!} \cdot \dfrac{j!}{(j-\ell)!\ell!} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \binom{n}{n-j} \binom{j}{\ell} \\ & = \binom{n}{n-j} \left( \sum_{\ell=1}^j ({-}1)^{\ell+1} \binom{j}{\ell}\right) \\ & =\binom{n}{n-j} \\ & =\binom{n-1+1}{n-j} \end{align*}For $2\leq i \leq n$
is given by
\begin{align*} \sum_{\ell=1}^n b_{1,\ell} a_{\ell,j} & =\sum_{\ell=1}^j b_{1,\ell} a_{\ell,j} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \binom{n}{\ell} \cdot \binom{n-\ell}{n-j} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \dfrac{n!}{(n-\ell)! \ell!} \cdot \dfrac{(n-\ell)!}{(n-j)!(j-\ell)!} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \dfrac{n!}{(n-j)! j!} \cdot \dfrac{j!}{(j-\ell)!\ell!} \\ & =\sum_{\ell=1}^j ({-}1)^{\ell+1} \binom{n}{n-j} \binom{j}{\ell} \\ & = \binom{n}{n-j} \left( \sum_{\ell=1}^j ({-}1)^{\ell+1} \binom{j}{\ell}\right) \\ & =\binom{n}{n-j} \\ & =\binom{n-1+1}{n-j} \end{align*}For $2\leq i \leq n$
 , $1\leq j\leq n$
, $1\leq j\leq n$ , the $(i,\,j)$
, the $(i,\,j)$ -entry of $BA$
-entry of $BA$ is given by
\begin{align*} \sum_{\ell=1}^n b_{i,\ell}a_{\ell,j}& =b_{i,i-1} a_{i-1,j} \\ & =a_{i-1,j} \\ & =\binom{n-i+1}{n-j}. \end{align*}
is given by
\begin{align*} \sum_{\ell=1}^n b_{i,\ell}a_{\ell,j}& =b_{i,i-1} a_{i-1,j} \\ & =a_{i-1,j} \\ & =\binom{n-i+1}{n-j}. \end{align*}
(2) For $1\leq i \leq n$
 , $1\leq j \leq n$
, $1\leq j \leq n$ , the $(i,\,j)$
, the $(i,\,j)$ -entry of $AD$
-entry of $AD$ is given by
\begin{align*} \sum_{\ell=1}^n a_{i,\ell}d_{\ell,j} & = a_{i,j}d_{j,j}+a_{i,j+1}d_{j+1,j} \\ & =a_{i, j}+a_{i,j+1} \\ & =\binom{n-i}{n-j}+\binom{n-i}{n-j-1} \\ & =\binom{n-i+1}{n-j}. \end{align*}It completes the proof of proposition 6.1
is given by
\begin{align*} \sum_{\ell=1}^n a_{i,\ell}d_{\ell,j} & = a_{i,j}d_{j,j}+a_{i,j+1}d_{j+1,j} \\ & =a_{i, j}+a_{i,j+1} \\ & =\binom{n-i}{n-j}+\binom{n-i}{n-j-1} \\ & =\binom{n-i+1}{n-j}. \end{align*}It completes the proof of proposition 6.1
Acknowledgements
This work was supported by JSPS KAKENHI grant number JP17K05263.