Refine search
Actions for selected content:
49 results
FOURTH-ORDER NONLINEAR SCHRÖDINGER EQUATION FOR APPLICATION TO CAPILLARY-GRAVITY WAVES IN DEEP WATER ON FLOWS OF BULK VORTICITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 18 November 2025, e37
-
- Article
-
- You have access
- HTML
- Export citation
Analytical insights on a behavioral macroeconomic model
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e135
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIFURCATION ANALYSIS AND FAST APPROACH OF A LESLIE-TYPE PREY–PREDATOR MODEL INVOLVING ALLEE EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 22 August 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability analysis and identification of high-yielding Amaranth accessions for varietal development under various agroecologies of Malawi
-
- Journal:
- Plant Genetic Resources / Volume 22 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 12 September 2024, pp. 333-341
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bespoke stability analysis tool in next-generation computational fluid dynamics solver
-
- Journal:
- The Aeronautical Journal / Volume 128 / Issue 1324 / June 2024
- Published online by Cambridge University Press:
- 23 November 2023, pp. 1164-1182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Dynamics of Flexible Aircraft with Small-Amplitude Vibrations
-
- Book:
- Dynamics of Flexible Aircraft
- Published online:
- 29 June 2023
- Print publication:
- 13 July 2023, pp 209-276
-
- Chapter
- Export citation
4 - Dynamics of Rigid Aircraft in a Nonstationary Atmosphere
-
- Book:
- Dynamics of Flexible Aircraft
- Published online:
- 29 June 2023
- Print publication:
- 13 July 2023, pp 133-173
-
- Chapter
- Export citation
Mathematical model and stability analysis on the transmission dynamics of skin sores
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e207
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A RANDOM ACCESS G-NETWORK: STABILITY, STABLE THROUGHPUT, AND QUEUEING ANALYSIS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 11 June 2019, pp. 111-137
-
- Article
- Export citation
MATHEMATICAL ANALYSIS OF COMBUSTION WAVES IN COMPETITIVE EXOTHERMIC REACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 339-342
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Dynamics of an Innovation Diffusion Model with Time Delay
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 455-481
- Print publication:
- August 2017
-
- Article
- Export citation
Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations: A Second-Order Scheme
- Part of
- Miscellaneous topics - Partial differential equations
- Partial differential equations, initial value and time-dependent initial-boundary value problems
- General theory in ordinary differential equations
- Real functions
- Computational aspects
- Finite fields and commutative rings (number-theoretic aspects)
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 1028-1048
- Print publication:
- October 2017
-
- Article
- Export citation
ON MODELLING THE TRANSITION TO TURBULENCE IN PIPE FLOW
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1-34
-
- Article
-
- You have access
- Export citation
Sharp-interface formation during lithium intercalation into silicon
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 March 2017, pp. 118-145
-
- Article
- Export citation
Pressure-Correction Projection FEM for Time-Dependent Natural Convection Problem
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 1090-1117
- Print publication:
- April 2017
-
- Article
- Export citation
Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 650-678
- Print publication:
- March 2017
-
- Article
- Export citation
Topological stability criteria for networking dynamical systems with Hermitian Jacobian
-
- Journal:
- European Journal of Applied Mathematics / Volume 27 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 888-903
-
- Article
- Export citation
Stable finite element approximation of a Cahn–Hilliard–Stokes system coupled to an electric field
-
- Journal:
- European Journal of Applied Mathematics / Volume 28 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 470-498
-
- Article
- Export citation
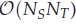 memory and
memory and  work, where
work, where 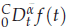 of order
of order 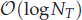 for
for 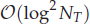 for
for 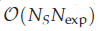 storage and
storage and 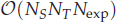 work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.
work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.