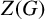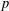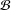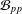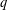Refine search
Actions for selected content:
10 results
2 - Algorithms for polycyclic groups
-
-
- Book:
- Groups St Andrews 2022 in Newcastle
- Published online:
- 21 November 2024
- Print publication:
- 12 December 2024, pp 53-73
-
- Chapter
- Export citation
A CHARACTERISATION OF SOLUBLE
 ${PST}$-GROUPS
${PST}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 520-527
- Print publication:
- December 2024
-
- Article
- Export citation
FINITE GROUPS WITH ABNORMAL MINIMAL NONNILPOTENT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 261-270
- Print publication:
- April 2023
-
- Article
- Export citation
ON EDGE-PRIMITIVE GRAPHS WITH SOLUBLE EDGE-STABILIZERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 160-187
- Print publication:
- October 2022
-
- Article
- Export citation
9 - Soluble Approximate Subgroups of GLn(C)
-
- Book:
- Introduction to Approximate Groups
- Published online:
- 31 October 2019
- Print publication:
- 14 November 2019, pp 147-169
-
- Chapter
- Export citation
NILPOTENCY IN UNCOUNTABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 27 October 2016, pp. 59-69
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ON SETS OF PP-GENERATORS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 241-249
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
SOME SOLUBILITY CRITERIA IN FACTORISED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 22-28
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
ZETA FUNCTIONS OF GROUPS: EULER PRODUCTS AND SOLUBLE GROUPS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 05 February 2002, pp. 149-154
-
- Article
-
- You have access
- Export citation
THE PROBABILITY OF GENERATING A FINITE SOLUBLE GROUP
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 81 / Issue 2 / September 2000
- Published online by Cambridge University Press:
- 19 October 2000, pp. 405-427
- Print publication:
- September 2000
-
- Article
- Export citation